超算子、泡利基和通道收缩

由Christopher Granade 撰写，量子计算研究所

在本指南中，我们将演示tensor_contract函数，该函数用于收缩Qobj的一个或多个索引对。例如，此功能可用于找到实现部分迹通道:math:S(rho) = Tr_2(rho)`的矩形超算子。使用此功能，我们可以快速将开放量子过程的系统-环境表示转换为超算子表示。

超算子表示与绘图

我们首先演示超算符的绘图，因为这将有助于我们可视化收缩通道的结果。

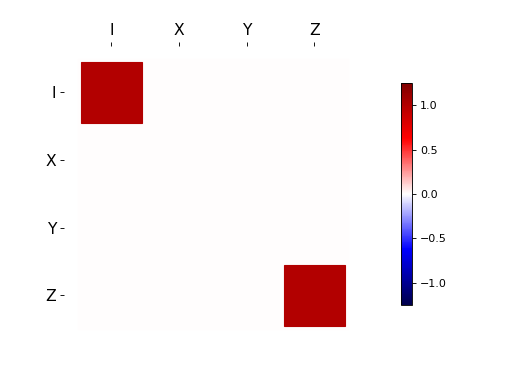
特别是，我们将使用由hinton实现的Hinton图，它显示矩阵元素的实部为正方形，其大小和颜色都对应于每个元素的大小。为了说明，我们首先绘制一些密度算子。

from qutip import hinton, identity, Qobj, to_super, sigmaz, tensor, tensor_contract
from qutip.core.gates import cnot, hadamard_transform

hinton(identity([2, 3]).unit())
hinton(Qobj([[1, 0.5], [0.5, 1]]).unit())
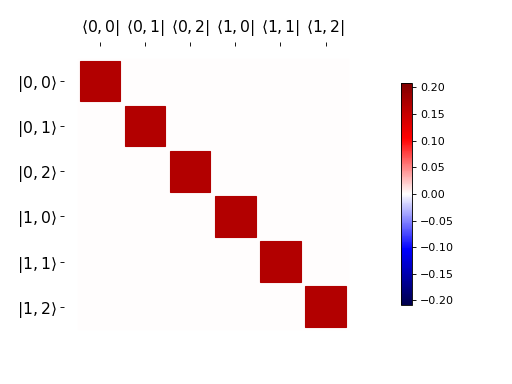
../_images/guide-super-1_00.png
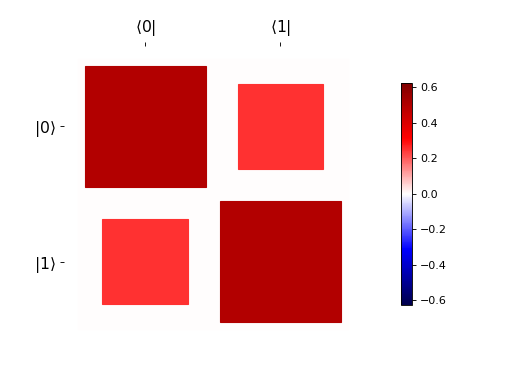
../_images/guide-super-1_01.png

我们将超算子表示为Pauli基中的矩阵，这样任何保持厄米性的映射都可以用实值矩阵表示。这对于使用Hinton图特别方便，因为该图因此携带了关于通道的完整信息。

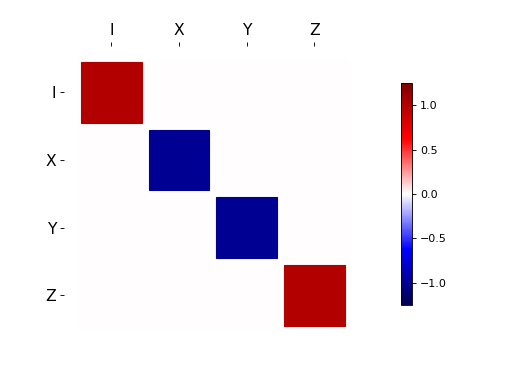
例如，通过\(\sigma_z\)的共轭操作，\(\mathbb{1}\)和\(\sigma_z\)保持不变，但\(\sigma_x\)和\(\sigma_y\)的符号会翻转。在Hinton图中，符号变化用负值方块表示，+1符号用正值方块表示。

hinton(to_super(sigmaz()))
../_images/guide-super-2.png

作为另外几个例子，我们还考虑了Hadamard变换和\(\sigma_z \otimes H\)的超矩阵。

hinton(to_super(hadamard_transform()))
hinton(to_super(tensor(sigmaz(), hadamard_transform())))
../_images/guide-super-3_00.png
../_images/guide-super-3_01.png

减少的通道

作为张量收缩的一个例子，我们现在考虑映射

\[S(\rho)=\Tr_2 (\scriptstyle \rm CNOT (\rho \otimes \ket{0}\bra{0}) \scriptstyle \rm CNOT^\dagger)\]

我们可以将这里的\(\scriptstyle \rm CNOT\)视为开放量子过程的系统-环境表示，其中环境寄存器被准备在状态\(\rho_{\text{anc}}\)中，然后一个幺正操作共同作用于感兴趣的系统和环境。最后，环境被追踪出来，仅在系统上留下一个通道。根据Wood diagrams ，这可以表示为准备映射、系统-环境幺正下的演化以及测量映射的组合。

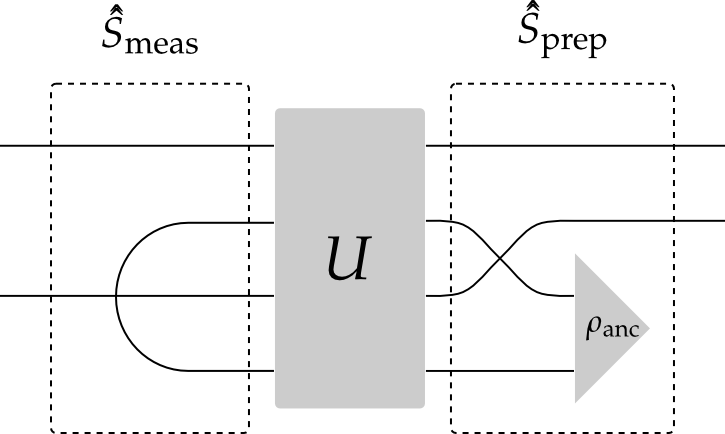
../_images/sprep-wood-diagram.png

左侧的两个张量线指示了我们必须进行张量收缩以获得测量映射的位置。 将张量线从0到3编号，这对应于tensor_contract的参数(1, 3)。

tensor_contract(to_super(identity([2, 2])), (1, 3))

同时，super_tensor 函数实现了右侧的交换，这样我们可以快速找到准备映射。

q = tensor(identity(2), basis(2))
s_prep = sprepost(q, q.dag())

对于一个\(\scriptstyle \rm CNOT\)系统-环境模型，这些映射的组合应该给我们一个完全去相干的通道。两个量子位上的通道只是超单位的\(\scriptstyle \rm CNOT\)通道：

hinton(to_super(cnot()))
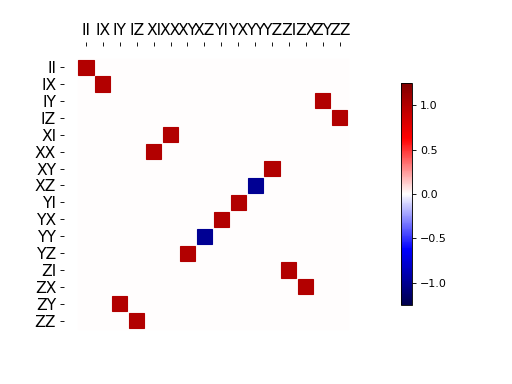
../_images/guide-super-6.png

我们现在通过将超酉\(\scriptstyle \rm CNOT\)与上面的准备通道相乘来完成，然后通过收缩第二个和第四个索引来应用部分迹通道。正如预期的那样，这给了我们一个去相位映射。

hinton(tensor_contract(to_super(cnot()), (1, 3)) * s_prep)
../_images/guide-super-7.png