使用张量积和部分迹
张量积
为了描述多体量子系统的状态——例如两个耦合的量子比特、一个量子比特与一个振荡器耦合等——我们需要通过取每个系统组件的状态向量的张量积来扩展希尔伯特空间。同样,作用于组合希尔伯特空间(描述耦合系统)中的状态向量的算子也是通过取各个算子的张量积来形成的。
在QuTiP中,函数tensor用于完成此任务。该函数以集合作为参数:
>>> tensor(op1, op2, op3)
或者一个 list:
>>> tensor([op1, op2, op3])
状态向量或运算符的复合量子对象,并返回组合希尔伯特空间的复合量子对象。该函数接受任意数量的状态或运算符作为参数。返回的量子对象类型与输入的类型相同。
例如,描述两个量子比特处于基态的状态向量是通过取两个单量子比特基态向量的张量积形成的:
print(tensor(basis(2, 0), basis(2, 0)))
输出:
Quantum object: dims = [[2, 2], [1, 1]], shape = (4, 1), type = ket
Qobj data =
[[1.]
[0.]
[0.]
[0.]]
或者等效地使用list格式:
print(tensor([basis(2, 0), basis(2, 0)]))
输出:
Quantum object: dims = [[2, 2], [1, 1]], shape = (4, 1), type = ket
Qobj data =
[[1.]
[0.]
[0.]
[0.]]
通过向tensor函数的参数列表中添加更多的分量状态向量,可以很容易地推广到更多的量子比特,如下例所示:
print(tensor((basis(2, 0) + basis(2, 1)).unit(), (basis(2, 0) + basis(2, 1)).unit(), basis(2, 0)))
输出:
Quantum object: dims = [[2, 2, 2], [1, 1, 1]], shape = (8, 1), type = ket
Qobj data =
[[0.5]
[0. ]
[0.5]
[0. ]
[0.5]
[0. ]
[0.5]
[0. ]]
这个状态稍微复杂一些,描述了两个量子比特在上下态之间的叠加,而第三个量子比特处于其基态。
为了构造作用于组合系统的扩展希尔伯特空间上的算子,我们同样将每个组件系统的算子列表传递给tensor函数。例如,要形成表示\(\sigma_x\)算子同时作用于两个量子比特的算子:
print(tensor(sigmax(), sigmax()))
输出:
Quantum object: dims = [[2, 2], [2, 2]], shape = (4, 4), type = oper, isherm = True
Qobj data =
[[0. 0. 0. 1.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[1. 0. 0. 0.]]
为了在组合的希尔伯特空间中创建仅作用于单个组件的操作符,我们取作用于感兴趣子空间的操作符的张量积,与对应于保持不变组件的恒等操作符。例如,表示在两量子位系统中第一个量子位上的\(\sigma_z\)操作符,同时不影响第二个量子位:
print(tensor(sigmaz(), identity(2)))
输出:
Quantum object: dims = [[2, 2], [2, 2]], shape = (4, 4), type = oper, isherm = True
Qobj data =
[[ 1. 0. 0. 0.]
[ 0. 1. 0. 0.]
[ 0. 0. -1. 0.]
[ 0. 0. 0. -1.]]
示例:构建复合哈密顿量
tensor 函数在构建复合系统的哈密顿量时被广泛使用。这里我们将看一些简单的例子。
两个耦合的量子比特
首先,让我们考虑一个由两个耦合的量子比特组成的系统。假设这两个量子比特具有相同的能量分裂,并且它们通过一个强度为 g = 0.05 的 \(\sigma_x\otimes\sigma_x\) 相互作用耦合(在裸量子比特能量分裂为单位的单位中)。描述这个系统的哈密顿量是:
H = tensor(sigmaz(), identity(2)) + tensor(identity(2), sigmaz()) + 0.05 * tensor(sigmax(), sigmax())
print(H)
输出:
Quantum object: dims = [[2, 2], [2, 2]], shape = (4, 4), type = oper, isherm = True
Qobj data =
[[ 2. 0. 0. 0.05]
[ 0. 0. 0.05 0. ]
[ 0. 0.05 0. 0. ]
[ 0.05 0. 0. -2. ]]
三个耦合的量子比特
双量子比特的例子很容易推广到三个耦合的量子比特:
H = (tensor(sigmaz(), identity(2), identity(2)) + tensor(identity(2), sigmaz(), identity(2)) + tensor(identity(2), identity(2), sigmaz()) + 0.5 * tensor(sigmax(), sigmax(), identity(2)) + 0.25 * tensor(identity(2), sigmax(), sigmax()))
print(H)
输出:
Quantum object: dims = [[2, 2, 2], [2, 2, 2]], shape = (8, 8), type = oper, isherm = True
Qobj data =
[[ 3. 0. 0. 0.25 0. 0. 0.5 0. ]
[ 0. 1. 0.25 0. 0. 0. 0. 0.5 ]
[ 0. 0.25 1. 0. 0.5 0. 0. 0. ]
[ 0.25 0. 0. -1. 0. 0.5 0. 0. ]
[ 0. 0. 0.5 0. 1. 0. 0. 0.25]
[ 0. 0. 0. 0.5 0. -1. 0.25 0. ]
[ 0.5 0. 0. 0. 0. 0.25 -1. 0. ]
[ 0. 0.5 0. 0. 0.25 0. 0. -3. ]]
与腔耦合的两能级系统:Jaynes-Cummings模型
光与物质相互作用的最简单的量子力学描述被封装在Jaynes-Cummings模型中,该模型描述了一个两能级原子与单模电磁场(腔模)之间的耦合。分别表示原子和腔的能量分裂为omega_a和omega_c,以及原子-腔相互作用强度为g,Jaynes-Cummings哈密顿量可以构造为:
N = 6
omega_a = 1.0
omega_c = 1.25
g = 0.75
a = tensor(identity(2), destroy(N))
sm = tensor(destroy(2), identity(N))
sz = tensor(sigmaz(), identity(N))
H = 0.5 * omega_a * sz + omega_c * a.dag() * a + g * (a.dag() * sm + a * sm.dag())
hinton(H, fig=plt.figure(figsize=(12, 12)))
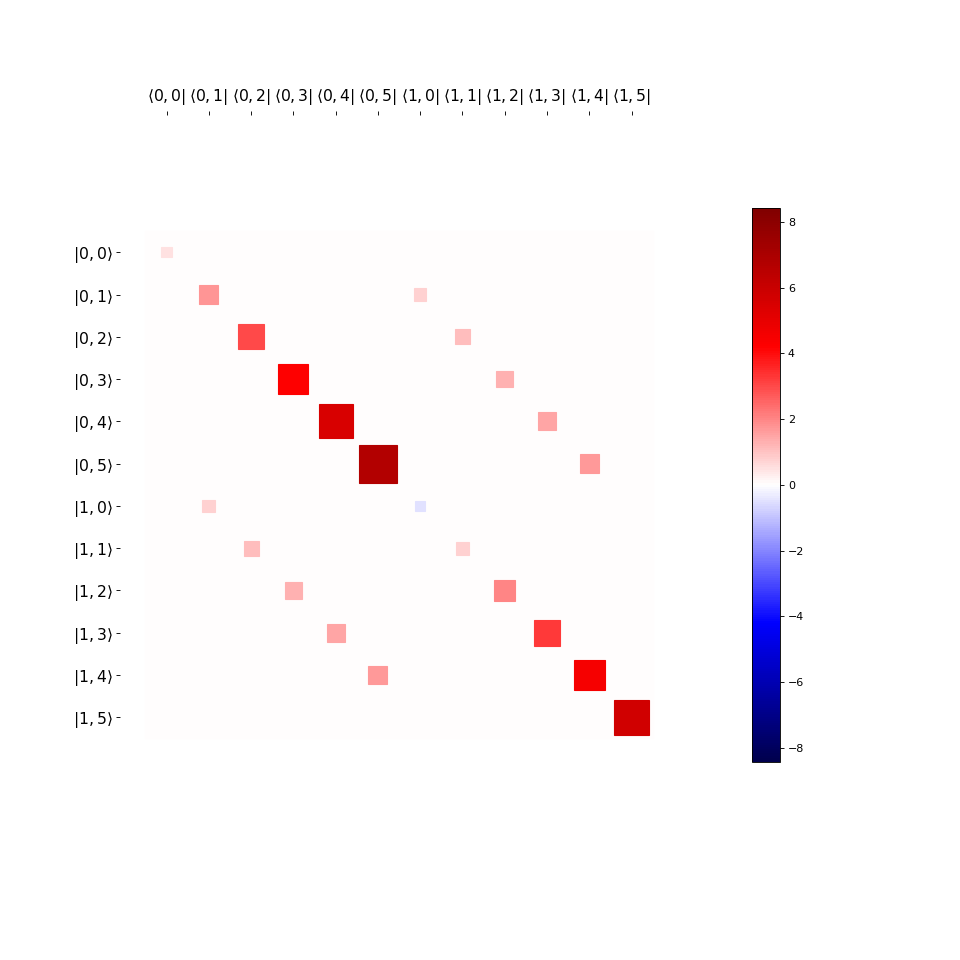
这里 N 是腔模中包含的Fock态的数量。
部分追踪
部分迹是一种通过平均(迹)消除某些自由度来减少希尔伯特空间维度的操作。在这个意义上,它因此是张量积的逆操作。当人们只对耦合量子系统的一部分感兴趣时,它是有用的。对于开放量子系统,这通常涉及对环境进行迹操作,只留下感兴趣的系统。在QuTiP中,类方法 ptrace 用于进行部分迹操作。ptrace 作用于调用它的 Qobj 实例,并且它接受一个参数 sel,这是一个整数列表,标记应该保留的组件系统。所有其他组件都被迹掉。
例如,描述从耦合的两量子比特系统中获得的单个量子比特的密度矩阵是通过以下方式获得的:
>>> psi = tensor(basis(2, 0), basis(2, 1))
>>> psi.ptrace(0)
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[1. 0.]
[0. 0.]]
>>> psi.ptrace(1)
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0.]
[0. 1.]]
请注意,部分迹总是导致密度矩阵(混合态),无论复合系统是纯态(由状态向量描述)还是混合态(由密度矩阵描述):
>>> psi = tensor((basis(2, 0) + basis(2, 1)).unit(), basis(2, 0))
>>> psi
Quantum object: dims = [[2, 2], [1, 1]], shape = (4, 1), type = ket
Qobj data =
[[0.70710678]
[0. ]
[0.70710678]
[0. ]]
>>> psi.ptrace(0)
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0.5 0.5]
[0.5 0.5]]
>>> rho = tensor(ket2dm((basis(2, 0) + basis(2, 1)).unit()), fock_dm(2, 0))
>>> rho
Quantum object: dims = [[2, 2], [2, 2]], shape = (4, 4), type = oper, isherm = True
Qobj data =
[[0.5 0. 0.5 0. ]
[0. 0. 0. 0. ]
[0.5 0. 0.5 0. ]
[0. 0. 0. 0. ]]
>>> rho.ptrace(0)
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0.5 0.5]
[0.5 0.5]]
超算符和张量操作
如超算符和向量化算符中所述,超算符是作用于Liouville空间的算符,即线性算符的向量空间。超算符可以使用同构\(\mathrm{vec} : \mathcal{L}(\mathcal{H}) \to \mathcal{H} \otimes \mathcal{H}\) [Hav03], [Wat13]来表示。为了表示作用于\(\mathcal{L}(\mathcal{H}_1 \otimes \mathcal{H}_2)\)的超算符,需要进行一些张量重排以获得所需的顺序\(\mathcal{H}_1 \otimes \mathcal{H}_2 \otimes \mathcal{H}_1 \otimes \mathcal{H}_2\)。
特别是,这意味着tensor不会像人们预期的那样作用于to_super的结果:
>>> A = qeye([2])
>>> B = qeye([3])
>>> to_super(tensor(A, B)).dims
[[[2, 3], [2, 3]], [[2, 3], [2, 3]]]
>>> tensor(to_super(A), to_super(B)).dims
[[[2], [2], [3], [3]], [[2], [2], [3], [3]]]
在前一种情况下,结果正确地包含了四个维度为 [2, 3] 的复合索引。然而,在后一种情况下,每个希尔伯特空间索引都被独立列出,并且顺序错误。
super_tensor 函数执行所需的重新排列,提供了与底层希尔伯特空间上的 tensor 最直接的类比。特别是,对于任何两个 type="oper" 的 Qobjs A 和 B,to_super(tensor(A, B)) == super_tensor(to_super(A), to_super(B)) 和 operator_to_vector(tensor(A, B)) == super_tensor(operator_to_vector(A), operator_to_vector(B))。回到前面的例子:
>>> super_tensor(to_super(A), to_super(B)).dims
[[[2, 3], [2, 3]], [[2, 3], [2, 3]]]
composite 函数根据其参数的 type 自动在 tensor 和 super_tensor 之间切换,使得 composite(A, B) 返回一个适当的 Qobj 来表示两个系统的组合。
>>> composite(A, B).dims
[[2, 3], [2, 3]]
>>> composite(to_super(A), to_super(B)).dims
[[[2, 3], [2, 3]], [[2, 3], [2, 3]]]
QuTiP 还允许更一般的张量操作,这些操作对于在超算符表示之间转换非常有用 [WBC11]。
特别是,tensor_contract 函数允许
收缩一个或多个索引对。
这可以用于找到表示部分迹映射的超算符。
使用此功能,我们可以构建一些非常奇特的映射,
例如从 \(3 \times 3\) 算子到 \(2 \times 2\)
算子的映射:
>>> tensor_contract(composite(to_super(A), to_super(B)), (1, 3), (4, 6)).dims
[[[2], [2]], [[3], [3]]]