操作状态和运算符
介绍
在之前的指南部分 量子对象的基本操作 中,我们看到了如何使用 QuTiP 内置的函数创建状态和操作符。在本部分指南中,我们将探讨如何使用状态和操作符执行基本操作。有关如何使用和操作这些对象的更详细演示,请参阅 教程 网页上的示例。
状态向量(kets 或 bras)
在这里,我们首先创建一个Fock basis 真空态向量 \(\left|0\right>\),在一个具有5个数字态的希尔伯特空间中,从0到4:
vac = basis(5, 0)
print(vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[1.]
[0.]
[0.]
[0.]
[0.]]
然后使用destroy函数创建一个对应于5个数字态的降阶算子\(\left(\hat{a}\right)\):
a = destroy(5)
print(a)
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = False
Qobj data =
[[0. 1. 0. 0. 0. ]
[0. 0. 1.41421356 0. 0. ]
[0. 0. 0. 1.73205081 0. ]
[0. 0. 0. 0. 2. ]
[0. 0. 0. 0. 0. ]]
现在让我们将破坏算子应用到我们的真空状态 vac,
print(a * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[0.]
[0.]
[0.]
[0.]]
我们看到,正如预期的那样,真空被转换为零向量。一个更有趣的例子来自于使用降阶算子的伴随算子,即升阶算子 \(\hat{a}^\dagger\):
print(a.dag() * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[1.]
[0.]
[0.]
[0.]]
提升算子确实将状态 vec 从真空状态提升到了 \(\left| 1\right>\) 状态。
除了使用 dagger Qobj.dag() 方法来提升状态外,我们还可以使用内置的 create 函数来创建一个提升算子:
c = create(5)
print(c * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[1.]
[0.]
[0.]
[0.]]
它做同样的事情。我们可以通过连续应用提升操作符多次提升真空态:
print(c * c * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0. ]
[0. ]
[1.41421356]
[0. ]
[0. ]]
或者只是取上升算符的平方 \(\left(\hat{a}^\dagger\right)^{2}\):
print(c ** 2 * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0. ]
[0. ]
[1.41421356]
[0. ]
[0. ]]
应用提升运算符两次给出了预期的\(\sqrt{n + 1}\)依赖关系。我们可以使用\(c * a\)的乘积来将数字运算符应用于状态向量vac:
print(c * a * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[0.]
[0.]
[0.]
[0.]]
或者在 \(\left| 1\right>\) 状态上:
print(c * a * (c * vac))
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[1.]
[0.]
[0.]
[0.]]
或\(\left| 2\right>\)状态:
print(c * a * (c**2 * vac))
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0. ]
[0. ]
[2.82842712]
[0. ]
[0. ]]
请注意,在最后一个例子中,应用数字运算符并没有给出预期的值 \(n=2\),而是 \(2\sqrt{2}\)。这是因为最后一个状态没有归一化为单位,如 \(c\left| n\right> = \sqrt{n+1}\left| n+1\right>\)。因此,我们应该首先归一化我们的向量:
print(c * a * (c**2 * vac).unit())
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[0.]
[2.]
[0.]
[0.]]
由于我们正在演示如何使用状态和操作符,我们做了比应该做的更多的工作。
例如,我们不需要在真空状态上操作来生成更高数量的Fock状态。
相反,我们可以使用basis(或fock)函数直接获取所需的状态:
ket = basis(5, 2)
print(ket)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[0.]
[1.]
[0.]
[0.]]
注意它是如何自动标准化的。我们也可以使用内置的num操作符:
n = num(5)
print(n)
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 2. 0. 0.]
[0. 0. 0. 3. 0.]
[0. 0. 0. 0. 4.]]
因此,我们使用c * a * (c ** 2 * vac).unit()来代替:
print(n * ket)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.]
[0.]
[2.]
[0.]
[0.]]
我们也可以创建状态的叠加:
ket = (basis(5, 0) + basis(5, 1)).unit()
print(ket)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0.70710678]
[0.70710678]
[0. ]
[0. ]
[0. ]]
在这里我们使用了Qobj.unit方法来再次归一化状态。再次使用数函数操作:
print(n * ket)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[0. ]
[0.70710678]
[0. ]
[0. ]
[0. ]]
我们还可以通过将displace和squeeze函数应用于真空态来创建相干态和压缩态:
vac = basis(5, 0)
d = displace(5, 1j)
s = squeeze(5, np.complex(0.25, 0.25))
print(d * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.60655682+0.j ]
[ 0. +0.60628133j]
[-0.4303874 +0.j ]
[ 0. -0.24104351j]
[ 0.14552147+0.j ]]
print(d * s * vac)
输出:
Quantum object: dims = [[5], [1]], shape = (5, 1), type = ket
Qobj data =
[[ 0.65893786+0.08139381j]
[ 0.10779462+0.51579735j]
[-0.37567217-0.01326853j]
[-0.02688063-0.23828775j]
[ 0.26352814+0.11512178j]]
当然,位移真空会产生一个相干态,这也可以使用内置的coherent函数来生成。
密度矩阵
QuTiP的主要目的之一是探索开放量子系统的动力学,其中系统的最一般状态不再是状态向量,而是密度矩阵。由于密度矩阵上的操作与向量上的操作相同,我们将简要介绍创建和使用这些结构。
最简单的密度矩阵是通过形成态矢量的外积 \(\left|\psi\right>\left<\psi\right|\) 来创建的:
ket = basis(5, 2)
print(ket * ket.dag())
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
类似的任务也可以通过 fock_dm 或 ket2dm 函数来完成:
print(fock_dm(5, 2))
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
print(ket2dm(ket))
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
如果我们想要创建一个密度矩阵,使其在\(\left|2\right>\)或\(\left|4\right>\)数态中被发现的经典概率相等,我们可以执行以下操作:
print(0.5 * ket2dm(basis(5, 4)) + 0.5 * ket2dm(basis(5, 2)))
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0. 0.5 0. 0. ]
[0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0.5]]
或者使用 0.5 * fock_dm(5, 2) + 0.5 * fock_dm(5, 4)。
还有一些其他内置函数用于创建预定义的密度矩阵,例如 coherent_dm 和 thermal_dm,它们分别创建相干态和热态密度矩阵。
print(coherent_dm(5, 1.25))
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0.20980701 0.26141096 0.23509686 0.15572585 0.13390765]
[0.26141096 0.32570738 0.29292109 0.19402805 0.16684347]
[0.23509686 0.29292109 0.26343512 0.17449684 0.1500487 ]
[0.15572585 0.19402805 0.17449684 0.11558499 0.09939079]
[0.13390765 0.16684347 0.1500487 0.09939079 0.0854655 ]]
print(thermal_dm(5, 1.25))
输出:
Quantum object: dims = [[5], [5]], shape = (5, 5), type = oper, isherm = True
Qobj data =
[[0.46927974 0. 0. 0. 0. ]
[0. 0.26071096 0. 0. 0. ]
[0. 0. 0.14483942 0. 0. ]
[0. 0. 0. 0.08046635 0. ]
[0. 0. 0. 0. 0.04470353]]
QuTiP 还提供了一组距离度量标准,用于确定两个密度矩阵分布之间的接近程度。包括迹距离 tracedist、保真度 fidelity、希尔伯特-施密特距离 hilbert_dist、Bures 距离 bures_dist、Bures 角度 bures_angle 和量子 Hellinger 距离 hellinger_dist。
x = coherent_dm(5, 1.25)
y = coherent_dm(5, np.complex(0, 1.25)) # <-- note the 'j'
z = thermal_dm(5, 0.125)
np.testing.assert_almost_equal(fidelity(x, x), 1)
np.testing.assert_almost_equal(hellinger_dist(x, y), 1.3819080728932833)
我们还知道,对于两个纯态,迹距离(T)和保真度(F)之间的关系是\(T = \sqrt{1 - F^{2}}\),而两个纯态\(\left|\psi\right>\)和\(\left|\phi\right>\)之间的量子Hellinger距离(QHE)由\(QHE = \sqrt{2 - 2\left|\left<\psi | \phi\right>\right|^2}\)给出。
np.testing.assert_almost_equal(tracedist(y, x), np.sqrt(1 - fidelity(y, x) ** 2))
对于一个纯态和一个混合态,\(1 - F^{2} \le T\) 也可以被验证:
assert 1 - fidelity(x, z) ** 2 < tracedist(x, z)
量子比特(两级)系统
在花费了大量时间研究表示谐振子态的基础态之后,我们现在转向量子比特,或两级量子系统(例如自旋-1/2)。为了创建一个对应于量子比特系统的状态向量,我们使用相同的basis,或fock函数,但只有两个级别:
spin = basis(2, 0)
此时,人们可能会问,这种状态与截断到两个能级的真空态中的谐振子状态有何不同?
vac = basis(2, 0)
在这个阶段,没有区别。这并不令人惊讶,因为我们调用了完全相同的函数两次。两者之间的区别来自于自旋算符 sigmax, sigmay, sigmaz, sigmap, 和 sigmam 对这两个能级状态的作用。例如,如果 vac 对应于谐振子的真空态,那么,正如我们已经看到的,我们可以使用升算符来得到 \(\left|1\right>\) 状态:
print(vac)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[1.]
[0.]]
c = create(2)
print(c * vac)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[0.]
[1.]]
对于一个自旋系统,类似于提升算符的算符是sigma-plus算符sigmap。作用于spin状态时,得到:
print(spin)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[1.]
[0.]]
print(sigmap() * spin)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[0.]
[0.]]
现在我们看到了区别!sigmap 操作符作用于 spin 状态时返回零向量。为什么会这样?为了了解发生了什么,让我们使用 sigmaz 操作符:
print(sigmaz())
输出:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[ 1. 0.]
[ 0. -1.]]
print(sigmaz() * spin)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[1.]
[0.]]
spin2 = basis(2, 1)
print(spin2)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[0.]
[1.]]
print(sigmaz() * spin2)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[ 0.]
[-1.]]
答案现在已经很明显了。由于QuTiP的sigmaz函数使用了sigma-z自旋算符的标准z基表示,spin状态对应于两级自旋系统的\(\left|\uparrow\right>\)状态,而spin2给出了\(\left|\downarrow\right>\)状态。因此,在我们之前的例子sigmap() * spin中,我们将量子比特状态从截断的两级希尔伯特空间中提升出来,导致了零状态。
虽然乍一看这个约定可能看起来有些奇怪,但实际上它非常方便。首先,自旋算子保持了传统的形式。其次,当自旋系统处于\(\left|\uparrow\right>\)状态时:
print(sigmaz() * spin)
输出:
Quantum object: dims = [[2], [1]], shape = (2, 1), type = ket
Qobj data =
[[1.]
[0.]]
非零分量是基础矩阵的第零个元素(记住Python使用C索引,矩阵从第零个元素开始)。因此,\(\left|\downarrow\right>\)状态在第一个索引位置有一个非零条目。这与量子信息中量子比特状态的定义很好地对应,其中激发的\(\left|\uparrow\right>\)状态被标记为\(\left|0\right>\),而\(\left|\downarrow\right>\)状态被标记为\(\left|1\right>\)。
如果想要为更高自旋系统创建自旋算符,那么jmat函数就派上用场了。
门
预定义的逻辑门如下表所示:
门函数 |
描述 |
|---|---|
绕x轴旋转 |
|
绕y轴旋转 |
|
绕z轴旋转 |
|
非门的平方根 |
|
非门的平方根 |
|
哈达玛门 |
|
相移门 |
|
在拉比脉冲下的量子比特旋转 |
|
受控 y 门 |
|
控制Z门 |
|
单量子比特旋转 |
|
S门的平方根 |
|
受控s门 |
|
受控 t 门 |
|
受控相位门 |
|
控制非门 |
|
与 cphase 相同 |
|
伯克利门 |
|
Swapalpha 门 |
|
交换两个量子比特的状态 |
|
交换门,带有01和10状态的额外相位 |
|
交换门的平方根 |
|
iswap门的平方根 |
|
弗雷德金门 |
|
莫尔-索伦森门 |
|
托佛利门 |
|
Hadamard 门 |
|
生成单量子比特上的Clifford群 |
|
全局相位门 |
要加载这个 qutip 模块,首先你需要导入 gates:
from qutip import gates
例如,使用Hadamard门:
H = gates.hadamard_transform()
print(H)
输出:
Quantum object: dims=[[2], [2]], shape=(2, 2), type='oper', dtype=Dense, isherm=True
Qobj data =
[[ 0.70710678 0.70710678]
[0.70710678 -0.70710678]]
期望值
关于量子系统的一些最重要信息来自于计算算符的期望值,无论是厄米特算符还是非厄米特算符,随着系统的状态或密度矩阵随时间变化。因此,在本节中,我们演示了如何使用expect函数。开始:
vac = basis(5, 0)
one = basis(5, 1)
c = create(5)
N = num(5)
np.testing.assert_almost_equal(expect(N, vac), 0)
np.testing.assert_almost_equal(expect(N, one), 1)
coh = coherent_dm(5, 1.0j)
np.testing.assert_almost_equal(expect(N, coh), 0.9970555745806597)
cat = (basis(5, 4) + 1.0j * basis(5, 3)).unit()
np.testing.assert_almost_equal(expect(c, cat), 0.9999999999999998j)
expect 函数也接受状态向量或密度矩阵的列表或数组作为第二个输入:
states = [(c**k * vac).unit() for k in range(5)] # must normalize
print(expect(N, states))
输出:
[0. 1. 2. 3. 4.]
cat_list = [(basis(5, 4) + x * basis(5, 3)).unit() for x in [0, 1.0j, -1.0, -1.0j]]
print(expect(c, cat_list))
输出:
[ 0.+0.j 0.+1.j -1.+0.j 0.-1.j]
注意在最后一个例子中,所有的返回值都是复数。这是因为expect函数会检查操作符是否是厄米的。如果操作符是厄米的,那么输出将始终是实数。在非厄米操作符的情况下,返回值可能是复数。因此,当输入是状态或密度矩阵的列表/数组时,expect函数将返回一个复数数组。
当然,expect 函数适用于自旋态和算符:
up = basis(2, 0)
down = basis(2, 1)
np.testing.assert_almost_equal(expect(sigmaz(), up), 1)
np.testing.assert_almost_equal(expect(sigmaz(), down), -1)
以及下一节中讨论的复合对象 使用张量积和部分迹:
spin1 = basis(2, 0)
spin2 = basis(2, 1)
two_spins = tensor(spin1, spin2)
sz1 = tensor(sigmaz(), qeye(2))
sz2 = tensor(qeye(2), sigmaz())
np.testing.assert_almost_equal(expect(sz1, two_spins), 1)
np.testing.assert_almost_equal(expect(sz2, two_spins), -1)
超算符和向量化运算符
除了状态向量和密度算子外,QuTiP 还允许使用 Kraus、Liouville 超矩阵和 Choi 矩阵形式来表示对密度算子进行线性操作的映射。这种支持基于作用于希尔伯特空间的线性算子与该希尔伯特空间的两个副本中的向量之间的对应关系, \(\mathrm{vec} : \mathcal{L}(\mathcal{H}) \to \mathcal{H} \otimes \mathcal{H}\) [Hav03], [Wat13].
这种同构在QuTiP中通过
operator_to_vector 和
vector_to_operator 函数实现:
psi = basis(2, 0)
rho = ket2dm(psi)
print(rho)
输出:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[1. 0.]
[0. 0.]]
vec_rho = operator_to_vector(rho)
print(vec_rho)
输出:
Quantum object: dims = [[[2], [2]], [1]], shape = (4, 1), type = operator-ket
Qobj data =
[[1.]
[0.]
[0.]
[0.]]
rho2 = vector_to_operator(vec_rho)
np.testing.assert_almost_equal((rho - rho2).norm(), 0)
Qobj.type 属性指示一个量子对象是否是一个对应于算子的向量(operator-ket),或者其厄米共轭(operator-bra)。
请注意,QuTiP 使用列堆叠约定来表示 \(\mathcal{L}(\mathcal{H})\) 和 \(\mathcal{H} \otimes \mathcal{H}\) 之间的同构关系:
A = Qobj(np.arange(4).reshape((2, 2)))
print(A)
输出:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[0. 1.]
[2. 3.]]
print(operator_to_vector(A))
输出:
Quantum object: dims = [[[2], [2]], [1]], shape = (4, 1), type = operator-ket
Qobj data =
[[0.]
[2.]
[1.]
[3.]]
由于 \(\mathcal{H} \otimes \mathcal{H}\) 是一个向量空间,该空间上的线性映射可以表示为矩阵,通常称为超算子。使用 Qobj、spre 和 spost 函数,可以快速构建分别对应于左乘和右乘的超矩阵。
X = sigmax()
S = spre(X) * spost(X.dag()) # Represents conjugation by X.
请注意,当给定type='oper'输入时,这是由to_super函数自动完成的。
S2 = to_super(X)
np.testing.assert_almost_equal((S - S2).norm(), 0)
表示超算子的量子对象由type='super'表示:
print(S)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[0. 0. 0. 1.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[1. 0. 0. 0.]]
关于超算子的信息,例如它们是否表示完全正映射,通过 Qobj.iscp、Qobj.istp 和 Qobj.iscptp 属性暴露:
print(S.iscp, S.istp, S.iscptp)
输出:
True True True
此外,在这个扩展空间上的动态生成器,通常称为Liouvillian超算符,可以使用liouvillian函数创建。每个生成器都接受一个哈密顿量和一个崩溃算符列表,并返回一个type="super"对象,该对象可以被指数化以找到该演化的超算符。
H = 10 * sigmaz()
c1 = destroy(2)
L = liouvillian(H, [c1])
print(L)
S = (12 * L).expm()
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = False
Qobj data =
[[ 0. +0.j 0. +0.j 0. +0.j 1. +0.j]
[ 0. +0.j -0.5+20.j 0. +0.j 0. +0.j]
[ 0. +0.j 0. +0.j -0.5-20.j 0. +0.j]
[ 0. +0.j 0. +0.j 0. +0.j -1. +0.j]]
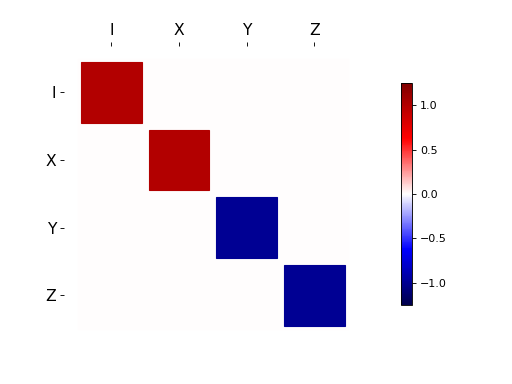
对于量子比特,一种特别有用的可视化超算符的方法是在泡利基中绘制它们,使得 \(S_{\mu,\nu} = \langle\!\langle \sigma_{\mu} | S[\sigma_{\nu}] \rangle\!\rangle\)。因为泡利基是厄米特的,所以对于所有保持厄米特的超算符 \(S\),\(S_{\mu,\nu}\) 是一个实数,这允许我们将 \(S\) 的元素绘制为 Hinton 图。在这样的图中,正元素用白色方块表示,负元素用黑色方块表示。每个元素的大小由相应方块的大小表示。例如,设 \(S[\rho] = \sigma_x \rho \sigma_x^{\dagger}\)。然后 \(S[\sigma_{\mu}] = \sigma_{\mu} \cdot \begin{cases} +1 & \mu = 0, x \\ -1 & \mu = y, z \end{cases}\)。我们可以通过注意到 \(S\) 的 Hinton 图中的 \(Y\) 和 \(Z\) 元素为负来快速看到这一点:
from qutip import *
settings.colorblind_safe = True
import matplotlib.pyplot as plt
plt.rcParams['savefig.transparent'] = True
X = sigmax()
S = spre(X) * spost(X.dag())
hinton(S)
Choi, Kraus, Stinespring 和 \(\chi\) 表示法
除了量子映射的超算子表示外,QuTiP 还支持其他几种有用的表示方法。首先,量子映射 \(\Lambda\) 的 Choi 矩阵 \(J(\Lambda)\) 对于处理辅助辅助过程断层扫描(AAPT)以及推理映射或通道的性质非常有用。在归一化之前,Choi 矩阵是通过在纠缠对的一半上作用 \(\Lambda\) 来定义的。在列堆叠约定中,
在QuTiP中,\(J(\Lambda)\) 可以通过在 type="super" 的 Qobj 上调用 to_choi 函数来找到。
X = sigmax()
S = sprepost(X, X)
J = to_choi(S)
print(J)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[0. 0. 0. 0.]
[0. 1. 1. 0.]
[0. 1. 1. 0.]
[0. 0. 0. 0.]]
print(to_choi(spre(qeye(2))))
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[1. 0. 0. 1.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[1. 0. 0. 1.]]
如果一个Qobj实例已经在Choi Qobj.superrep中,那么调用to_choi将不会做任何事情:
print(to_choi(J))
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[0. 0. 0. 0.]
[0. 1. 1. 0.]
[0. 1. 1. 0.]
[0. 0. 0. 0.]]
要返回到超算子表示,只需使用to_super函数。
与to_choi一样,to_super是幂等的:
print(to_super(J) - S)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
print(to_super(S))
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[0. 0. 0. 1.]
[0. 0. 1. 0.]
[0. 1. 0. 0.]
[1. 0. 0. 0.]]
我们可以通过特征分解从Choi矩阵快速获得另一个有用的表示。 特别是,设\(\{A_i\}\)为一组算子,使得 \(J(\Lambda) = \sum_i |A_i\rangle\!\rangle \langle\!\langle A_i|\)。 对于任何保持厄米性的映射,即对于任何映射\(\Lambda\)使得\(J(\Lambda) = J^\dagger(\Lambda)\),我们可以以这种方式写出\(J(\Lambda)\)。 这些算子随后形成\(\Lambda\)的Kraus表示。特别是,对于任何输入\(\rho\),
注意使用列堆叠恒等式 \((C^\mathrm{T} \otimes A) |B\rangle\!\rangle = |ABC\rangle\!\rangle\),我们有
保持厄米性的映射的Kraus表示可以在QuTiP中使用to_kraus函数找到。
del sum # np.sum overwrote sum and caused a bug.
I, X, Y, Z = qeye(2), sigmax(), sigmay(), sigmaz()
S = sum([sprepost(P, P) for P in (I, X, Y, Z)]) / 4
print(S)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True
Qobj data =
[[0.5 0. 0. 0.5]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]
[0.5 0. 0. 0.5]]
J = to_choi(S)
print(J)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = choi
Qobj data =
[[0.5 0. 0. 0. ]
[0. 0.5 0. 0. ]
[0. 0. 0.5 0. ]
[0. 0. 0. 0.5]]
print(J.eigenstates()[1])
输出:
[Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[1.]
[0.]
[0.]
[0.]]
Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[0.]
[1.]
[0.]
[0.]]
Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[0.]
[0.]
[1.]
[0.]]
Quantum object: dims = [[[2], [2]], [1, 1]], shape = (4, 1), type = operator-ket
Qobj data =
[[0.]
[0.]
[0.]
[1.]]]
K = to_kraus(S)
print(K)
输出:
[Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0.70710678 0. ]
[0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[0. 0. ]
[0.70710678 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[0. 0.70710678]
[0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0. ]
[0. 0.70710678]]]
与其他表示转换函数一样,to_kraus
会检查其输入的Qobj.superrep属性,并选择合适的转换方法。因此,在上面的例子中,我们也可以对J调用to_kraus。
KJ = to_kraus(J)
print(KJ)
输出:
[Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0.70710678 0. ]
[0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[0. 0. ]
[0.70710678 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = False
Qobj data =
[[0. 0.70710678]
[0. 0. ]], Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0. ]
[0. 0.70710678]]]
for A, AJ in zip(K, KJ):
print(A - AJ)
输出:
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0.]
[0. 0.]]
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0.]
[0. 0.]]
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0.]
[0. 0.]]
Quantum object: dims = [[2], [2]], shape = (2, 2), type = oper, isherm = True
Qobj data =
[[0. 0.]
[0. 0.]]
Stinespring表示与Kraus表示密切相关,由一对运算符\(A\)和\(B\)组成,使得对于所有作用于\(\mathcal{H}\)的运算符\(X\),
其中部分迹是对应于Kraus求和中的索引的新索引上的部分迹。转换为Stinespring表示由to_stinespring函数处理。
a = create(2).dag()
S_ad = sprepost(a * a.dag(), a * a.dag()) + sprepost(a, a.dag())
S = 0.9 * sprepost(I, I) + 0.1 * S_ad
print(S)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = False
Qobj data =
[[1. 0. 0. 0.1]
[0. 0.9 0. 0. ]
[0. 0. 0.9 0. ]
[0. 0. 0. 0.9]]
A, B = to_stinespring(S)
print(A)
输出:
Quantum object: dims = [[2, 3], [2]], shape = (6, 2), type = oper, isherm = False
Qobj data =
[[-0.98845443 0. ]
[ 0. 0.31622777]
[ 0.15151842 0. ]
[ 0. -0.93506452]
[ 0. 0. ]
[ 0. -0.16016975]]
print(B)
输出:
Quantum object: dims = [[2, 3], [2]], shape = (6, 2), type = oper, isherm = False
Qobj data =
[[-0.98845443 0. ]
[ 0. 0.31622777]
[ 0.15151842 0. ]
[ 0. -0.93506452]
[ 0. 0. ]
[ 0. -0.16016975]]
请注意,已经添加了一个新的索引,使得 \(A\) 和 \(B\) 的维度为 [[2, 3], [2]],其中长度为3的索引表示Choi矩阵的秩为3(或者说,该映射有三个Kraus算子)。
to_kraus(S)
print(to_choi(S).eigenenergies())
输出:
[0. 0.04861218 0.1 1.85138782]
最后,QuTiP支持的最后一个超算子表示是\(\chi\)-矩阵表示,
其中 \(\{B_\alpha\}\) 是作用于 \(\mathcal{H}\) 空间的矩阵的基。在 QuTiP 中,这个基被取为泡利基 \(B_\alpha = \sigma_\alpha / \sqrt{2}\)。转换为 \(\chi\) 形式由 to_chi 函数处理。
chi = to_chi(S)
print(chi)
输出:
Quantum object: dims = [[[2], [2]], [[2], [2]]], shape = (4, 4), type = super, isherm = True, superrep = chi
Qobj data =
[[3.7+0.j 0. +0.j 0. +0.j 0.1+0.j ]
[0. +0.j 0.1+0.j 0. +0.1j 0. +0.j ]
[0. +0.j 0. -0.1j 0.1+0.j 0. +0.j ]
[0.1+0.j 0. +0.j 0. +0.j 0.1+0.j ]]
\(\chi\) 矩阵的一个便利特性是,与恒等映射的平均门保真度可以直接从 \(\chi_{00}\) 元素中读取:
np.testing.assert_almost_equal(average_gate_fidelity(S), 0.9499999999999998)
print(chi[0, 0] / 4)
输出:
(0.925+0j)
在这里,因子4来自于底层希尔伯特空间\(\mathcal{H}\)的维度。与超算符和Choi表示一样,\(\chi\)表示由Qobj.superrep表示,使得to_super、to_choi、to_kraus、to_stinespring和to_chi都从\(\chi\)表示适当地转换。
量子映射的性质
除了在不同量子映射表示之间进行转换外,QuTiP 还提供了属性,以便轻松检查映射是否完全正、保迹和/或保厄米性。每个属性都使用 Qobj.superrep 来自动执行任何所需的转换。
特别是,如果一个量子映射将所有正算子映射到正算子,则称其为正映射(但不一定是完全正映射)。例如,转置映射 \(\Lambda(\rho) = \rho^{\mathrm{T}}\) 是一个正映射。然而,如果我们与恒等映射进行张量积以得到部分转置映射,就会遇到问题。
rho = ket2dm(bell_state())
rho_out = partial_transpose(rho, [0, 1])
print(rho_out.eigenenergies())
输出:
[-0.5 0.5 0.5 0.5]
请注意,即使我们从一个正映射开始,我们也得到了一个具有负特征值的算子。完全正性通过要求映射对所有正算子返回正算子来解决这个问题,并且即使在与其他映射张量积时也是如此。Choi矩阵在这里非常有用,因为可以证明一个映射是完全正性的当且仅当其Choi矩阵是正性的[Wat13]。QuTiP通过Qobj.iscp属性实现了这一检查。作为一个例子,请注意上面的代码片段已经通过作用于纠缠对的一半来计算转置映射的Choi矩阵。我们只需要手动设置dims和superrep属性以反映底层希尔伯特空间的结构和所选择的表示。
J = rho_out
J.dims = [[[2], [2]], [[2], [2]]]
J.superrep = 'choi'
print(J.iscp)
输出:
False
这证实了转置映射不是完全正的。另一方面,转置映射确实满足一个较弱的条件,即它是保持厄米性的。也就是说,对于所有满足\(\rho = \rho^\dagger\)的\(\rho\),有\(\Lambda(\rho) = (\Lambda(\rho))^\dagger\)。为了看到这一点,我们注意到\((\rho^{\mathrm{T}})^\dagger = \rho^*\),即\(\rho\)的复共轭。根据假设,\(\rho = \rho^\dagger = (\rho^*)^{\mathrm{T}}\),因此\(\Lambda(\rho) = \Lambda(\rho^\dagger) = \rho^*\)。我们可以通过检查Qobj.ishp属性来确认这一点:
print(J.ishp)
输出:
True
接下来,我们注意到转置映射确实保留了其输入的迹,即对于所有的 \(\rho\),有 \(\operatorname{Tr}(\Lambda[\rho]) = \operatorname{Tr}(\rho)\)。
这可以通过 Qobj.istp 属性来确认:
print(J.istp)
输出:
False
最后,如果一个映射总是将有效状态映射到有效状态,则称为量子通道。形式上,如果一个映射既是完全正定的又是保迹的,则它是一个通道。因此,QuTiP 提供了一个单一属性来快速检查这一点是否成立。
>>> print(J.iscptp)
False
>>> print(to_super(qeye(2)).iscptp)
True