开放量子系统的环境

作者 Paul Menczel 和 Gerardo Suarez

QuTiP 可以描述开放量子系统的环境。它们可以被传递给各种求解器，在这些求解器中，它们的影响会被精确或近似地考虑进去。接下来，我们将讨论玻色子和费米子的热环境。在我们的定义中，我们遵循 [BoFiN23]。

请注意，目前我们每个环境仅支持一个耦合项。如果更通用的耦合对您有用，请在GitHub上告诉我们。

玻色子环境

一个玻色环境由一系列连续谐振子描述。因此，开放量子系统及其环境由哈密顿量描述。

\[H = H_{\rm s} + Q \otimes X + \sum_k \hbar\omega_k\, a_k^\dagger a_k , \qquad X = \sum_k g_k (a_k + a_k^\dagger)\]

（在单个玻色环境的情况下）。这里，\(H_{\rm s}\) 是开放系统的哈密顿量，\(Q\) 是系统耦合算子。求和部分列举了具有频率 \(\omega_k\) 和耦合 \(g_k\) 的环境模式。耦合由谱密度描述

\[J(\omega) = \pi \sum_k g_k^2 \delta(\omega - \omega_k) .\]

同样地，一个玻色环境可以通过其自相关函数来描述

\[C(t) = \langle X(t) X \rangle = \sum_{k} g_{k}^{2} \Big( \cos(\omega_{k} t) \underbrace{( 2 n_{k}+1)}_{\coth(\frac{\beta \omega_{k}}{2})} - i \sin(\omega_{k} t) \Big)\]

（其中 \(X(t)\) 是相互作用图像算子）或其功率谱

\[S(\omega) = \int_{-\infty}^\infty \mathrm dt\, C(t)\, \mathrm e^{\mathrm i\omega t} ,\]

这是相关函数的逆傅里叶变换。相关函数满足对称关系 \(C(-t) = C(t)^\ast\)。

假设初始状态是温度为\(\beta\)的热态，在连续极限下，相关函数和功率谱可以通过谱密度计算得出。

(1)\[\begin{split}\begin{aligned} C(t) &= \int_0^\infty \frac{\mathrm d\omega}{\pi}\, J(\omega) \Bigl[ \coth\Bigl( \frac{\beta\omega}{2} \Bigr) \cos\bigl( \omega t \bigr) - \mathrm i \sin\bigl( \omega t \bigr) \Bigr] , \\ S(\omega) &= \operatorname{sign}(\omega)\, J(|\omega|) \Bigl[ \coth\Bigl( \frac{\beta\omega}{2} \Bigr) + 1 \Bigr] . \end{aligned}\end{split}\]

在这里，\(\operatorname{sign}(\omega) = \pm 1\) 取决于 \(\omega\) 的符号。在零温度下，这些方程变为 \(C(t) = \int_0^\infty \frac{\mathrm d\omega}{\pi} J(\omega) \mathrm e^{-\mathrm i\omega t}\) 和 \(S(\omega) = 2 \Theta(\omega) J(|\omega|)\)，其中 \(\Theta\) 是 Heaviside 函数。

如果环境与开放系统的耦合较弱，环境会以跃迁速率\(\gamma \propto S(-\Delta\omega)\)诱导量子跃迁，其中\(\Delta\omega\)是系统对应于量子跃迁的能量变化。在强耦合情况下，QuTiP提供了基于相关函数的多指数分解的精确积分方法，见下文。

注意

我们通常假设频率 \(\omega_k\) 都是正的，因此对于 \(\omega \leq 0\)，\(J(\omega) = 0\)。为了处理在负频率处有支持的谱密度 \(J(\omega)\)，可以使用有效谱密度 \(J'(\omega) = J(\omega) - J(-\omega)\)。这个过程可能会产生所需的关联函数，因为

\[\int_0^\infty \frac{\mathrm d\omega}{\pi}\, J'(\omega) \bigl[ \cdots \bigr] = \int_{-\infty}^\infty \frac{\mathrm d\omega}{\pi}\, J(\omega) \bigl[ \cdots \bigr] ,\]

其中 \([\cdots]\) 代表方程 (1) 中的方括号。但请注意，方程 (1) 的推导在这种情况下是无效的，因为环境没有热态。

注意

请注意，上面提供的\(S(\omega)\)表达式在\(\omega=0\)时是未定义的。对于零温度，我们简单地有\(S(0) = 0\)。

对于非零温度，可以得到

\[S(0) = 2\beta^{-1}\, J'(0) .\]

因此，如果光谱密度是亚欧姆的，\(S(0)\) 会发散。

预定义环境

欧姆环境

欧姆环境可以在QuTiP中使用类OhmicEnvironment来构建。它们的特征是通过以下形式的谱密度来描述的。

(2)\[J(\omega) = \alpha \frac{\omega^s}{\omega_c^{s-1}} e^{-\omega / \omega_c} ,\]

其中 \(\alpha\) 是一个表示耦合强度的无量纲参数， \(\omega_{c}\) 是截止频率，\(s\) 是一个决定低频行为的参数。欧姆环境通常根据这个参数分类为

亚欧姆 (\(s<1\))
欧姆 (\(s=1\))
超欧姆 (\(s>1\)).

注意

在文献中，欧姆谱密度通常可以表示为 \(J(\omega) = \alpha \frac{\omega^s}{\omega_c^{s-1}} f(\omega)\)，其中 \(f(\omega)\) 满足 \(\lim\limits_{\omega \to \infty} f(\omega) = 0\)，被称为截止函数。截止函数确保谱密度及其积分（例如 (1)）不会发散。有时，对于亚欧姆谱密度，也会使用红外截止，使得 \(\lim\limits_{\omega \to 0} J(\omega) = 0\)。这个预定义的欧姆环境类仅限于指数截止函数，这是文献中最常用的之一。其他截止函数可以在 QuTiP 中使用用户定义的环境，如下所述。

将欧姆谱密度 (2) 代入 (1)，相关函数可以解析计算：

\[C(t)= \frac{\alpha}{\pi} w_{c}^{1-s} \beta^{-(s+1)} \Gamma(s+1) \left[ \zeta\left(s+1,\frac{1+\beta w_{c} -i w_{c} t}{\beta w_{c}} \right) +\zeta\left(s+1,\frac{1+ i w_{c} t}{\beta w_{c}}\right) \right] ,\]

其中 \(\beta\) 是逆温度，\(\Gamma\) 是伽玛函数，\(\zeta\) 是赫维茨 zeta 函数。零温度情况可以通过取极限 \(\beta \to \infty\) 获得，结果是

\[C(t) = \frac{\alpha}{\pi} \omega_c^2\, \Gamma(s+1) (1+ i \omega_{c} t)^{-(s+1)} .\]

对于复参数的zeta函数的评估需要mpmath，因此Ohmic环境的某些功能只有在安装了mpmath时才可用。

可以通过拟合程序approx_by_cf_fit和approx_by_sd_fit获得Ohmic环境的多指数近似。以下示例展示了如何创建亚Ohmic环境，以及如何使用approx_by_cf_fit来拟合相关函数的实部和虚部，每个部分使用两个指数项。

import numpy as np
import qutip as qt
import matplotlib.pyplot as plt

# Define a sub-Ohmic environment with the given temperature, coupling strength and cutoff
env = qt.OhmicEnvironment(T=0.1, alpha=1, wc=3, s=0.7)

# Fit the correlation function with three exponential terms
tlist = np.linspace(0, 3, 250)
approx_env, info = env.approx_by_cf_fit(tlist, target_rsme=None, Nr_max=3, Ni_max=3, maxfev=1e8)

这里创建的环境 approx_env 可以用于例如 HEOM 求解器。变量 info 包含有关拟合收敛的信息；在这里，我们将绘制拟合结果与分析相关函数。请注意，更多的指数项可能会产生更好的结果。

plt.plot(tlist, np.real(env.correlation_function(tlist)), label='Real part (analytic)')
plt.plot(tlist, np.real(approx_env.correlation_function(tlist)), '--', label='Real part (fit)')

plt.plot(tlist, np.imag(env.correlation_function(tlist)), label='Imag part (analytic)')
plt.plot(tlist, np.imag(approx_env.correlation_function(tlist)), '--', label='Imag part (fit)')

plt.xlabel('Time')
plt.ylabel('Correlation function')
plt.tight_layout()
plt.legend()

Drude-Lorentz 环境

Drude-Lorentz环境，也称为过阻尼环境，可以在QuTiP中使用类DrudeLorentzEnvironment来构建。它们以形式的光谱密度为特征

\[J(\omega) = \frac{2 \lambda \gamma \omega}{\gamma^{2}+\omega^{2}} ,\]

其中 \(\lambda\) 是耦合强度（具有能量的量纲），\(\gamma\) 是截止频率。

要计算相应的相关函数，可以应用松原展开：

\[C(t) = \sum_{k=0}^{\infty} c_k e^{- \nu_k t}\]

这个展开式的系数是

\[\begin{split}\nu_{k} = \begin{cases} \gamma & k = 0\\ {2 \pi k} / {\beta} & k \geq 1\\ \end{cases} \;, \qquad c_k = \begin{cases} \lambda \gamma [\cot(\beta \gamma / 2) - i] & k = 0\\ \frac{4 \lambda \gamma \nu_k }{ (\nu_k^2 - \gamma^2)\beta} & k \geq 1\\ \end{cases} \;.\end{split}\]

函数 approx_by_matsubara 通过在一个有限的索引 \(N_k\) 处截断这个级数，创建了一个多指数近似来模拟 Drude-Lorentz 环境。例如，这个近似可以与 HEOM 求解器一起使用。本指南的 HEOM 部分包含了更多使用 Drude-Lorentz 环境的示例。

同样地，函数 approx_by_pade 可以用来应用并截断数值上更高效的Padé展开。

欠阻尼环境

在QuTiP中可以使用类UnderDampedEnvironment来构建欠阻尼环境。它们的特点是具有以下形式的光谱密度

\[J(\omega) = \frac{\lambda^{2} \Gamma \omega}{(\omega_0^{2}- \omega^{2})^{2}+ \Gamma^{2} \omega^{2}} ,\]

其中 \(\lambda\), \(\Gamma\) 和 \(\omega_0\) 分别是耦合强度（具有维度 \((\text{energy})^{3/2}\)）、截止频率和共振频率。

类似于Drude-Lorentz环境，相关函数可以通过Matsubara展开来近似。此功能可通过approx_by_matsubara函数使用。

对于低温情况，Matsubara展开收敛较慢。建议使用拟合程序来处理Matsubara贡献，如[Lambert19]中所述。

用户自定义环境

如引言所述，玻色环境完全由其温度和光谱密度（SD）表征，或者由其相关函数（CF）或功率谱（PS）表征。QuTiP允许通过指定光谱密度、相关函数或功率谱来创建用户定义的环境。

QuTiP 然后根据提供的函数计算其他两个函数。为此，它使用公式 \(S(\omega) = \operatorname{sign}(\omega)\, J(|\omega|) \bigl[ \coth( \beta\omega / 2 ) + 1 \bigr]\) 在 SD 和 PS 之间进行转换，并使用快速傅里叶变换在 PS 和 CF 之间进行转换。前者的转换需要指定浴温度；后者需要提供一个截止频率（或截止时间）以及指定的函数（SD、CF 或 PS）。通过这种方式，可以从指定的函数计算出所有特征函数。

以下示例手动创建了一个具有欠阻尼谱密度的环境。然后，它比较了通过快速傅里叶变换获得的相关函数与松原展开式。在\(t=0\)附近可以看到松原展开式的缓慢收敛性。

# Define underdamped environment parameters
T = 0.1
lam = 1
gamma = 2
w0 = 5

# User-defined environment based on SD
def underdamped_sd(w):
    return lam**2 * gamma * w / ((w**2 - w0**2)**2 + (gamma*w)**2)
env = qt.BosonicEnvironment.from_spectral_density(underdamped_sd, wMax=50, T=T)

tlist = np.linspace(-2, 2, 250)
plt.plot(tlist, np.real(env.correlation_function(tlist)), label='FFT')

# Pre-defined environment and Matsubara approximations
env2 = qt.UnderDampedEnvironment(T, lam, gamma, w0)
for Nk in range(0, 11, 2):
    approx_env = env2.approx_by_matsubara(Nk)
    plt.plot(tlist, np.real(approx_env.correlation_function(tlist)), label=f'Nk={Nk}')

plt.xlabel('Time')
plt.ylabel('Correlation function (real part)')
plt.tight_layout()
plt.legend()

多指数近似

许多模拟与强耦合环境的开放量子系统动力学的方法假设环境相关函数可以通过多指数展开来近似，如下所示：

\[C(t) = C_R(t) + \mathrm i C_I(t) , \qquad C_{R,I}(t) = \sum_{k=1}^{N_{R,I}} c^{R,I}_k \exp[-\nu^{R,I}_k t]\]

使用少量的指数\(N_{R,I}\)。注意\(C_R(t)\)和\(C_I(t)\)是相关函数的实部和虚部，但系数\(c^{R,I}_k\)和指数\(\nu^{R,I}_k\)通常不需要是实数。

在前面的章节中，介绍了获取多指数近似的各种方法。这些近似函数的输出是ExponentialBosonicEnvironment对象。一个ExponentialBosonicEnvironment基本上是一个CFExponent的集合，它存储（在玻色子情况下）系数、指数以及指数是否对实部、虚部或两者都有贡献。正如我们上面已经看到的，然后可以计算与指数对应的谱密度、相关函数和功率谱，以便将它们与原始的、精确的环境进行比较。

让 \(c_k \mathrm e^{-\nu_k t}\) 成为相关函数中的一个项（即 \(c_k = c^R_k\) 或 \(c_k = \mathrm i c^I_k\)）。功率谱中的相应项为

\[S_k(\omega) = 2\Re\Bigr[ \frac{c_k}{\nu_k - \mathrm i\omega} \Bigr]\]

并且，如果已经指定了温度，则可以按照上述方法计算光谱密度中的相应项。

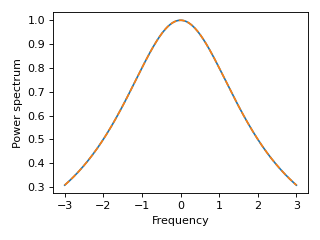
以下示例展示了如何为简单示例手动创建一个ExponentialBosonicEnvironment，其中\(C(t) = c \mathrm e^{-\nu t}\)，且\(c\)和\(\nu\)为实数。功率谱则为洛伦兹型，\(S(\omega) = 2c\nu / (\nu^2 + \omega^2)\)。

c = 1
nu = 2
wlist = np.linspace(-3, 3, 250)

env = qt.ExponentialBosonicEnvironment([c], [nu], [], [])

plt.figure(figsize=(4, 3))
plt.plot(wlist, env.power_spectrum(wlist))
plt.plot(wlist, 2 * c * nu / (nu**2 + wlist**2), '--')
plt.xlabel('Frequency')
plt.ylabel('Power spectrum')
plt.tight_layout()

费米子环境

QuTiP中费米子环境的实现尚未像玻色子环境那样先进。目前，用户自定义的费米子环境和拟合尚未实现。

然而，QuTiP中费米子环境的整体结构与玻色子环境类似。有一个预定义的费米子环境，即洛伦兹环境，以及多指数费米子环境。洛伦兹环境可以通过多指数Matsubara或Padé展开来近似。

在费米子情况下，我们考虑数守恒的哈密顿量

\[H = H_s + (B^\dagger c + c^\dagger B) + \sum_k \hbar\omega_k\, b^\dagger_k b_k , \qquad B = \sum_k f_k b_k ,\]

其中浴操作符 \(b_k\) 和系统操作符 \(c\) 遵循费米子反对易关系。与玻色子情况类似，我们定义了谱密度

\[J(\omega) = 2\pi \sum_k f_k^2\, \delta[\omega - \omega_k] ,\]

然而，现在可以为所有（包括负）频率定义，因为每个模式的频谱都是有界的。

费米子环境的特征可以通过其谱密度、逆温度 \(\beta\) 和化学势 \(\mu\) 来描述，或者等效地通过两个相关函数或两个功率谱来描述。相关函数是

\[C^\sigma(t) = \langle B^\sigma(t) B^{-\sigma} \rangle = \int_{-\infty}^\infty \frac{\mathrm d\omega}{2\pi}\, J(\omega)\, \mathrm e^{\sigma \mathrm i\omega t}\, f_F(\sigma \beta[\omega - \mu]) ,\]

其中 \(\sigma = \pm 1\), \(B^+ = B^\dagger\) 和 \(B^- = B\)。此外，\(f_F(x) = (\mathrm e^x + 1)^{-1}\) 是费米-狄拉克函数。请注意，我们仍然有 \(C^\sigma(-t) = C^\sigma(t)^\ast\)。功率谱是相关函数的傅里叶变换，

\[S^\sigma(\omega) = \int_{-\infty}^\infty \mathrm dt\, C^\sigma(t)\, \mathrm e^{-\sigma \mathrm i\omega t} = J(\omega) f_F(\sigma\beta[\omega - \mu]) .\]

由于 \(f_F(x) + f_F(-x) = 1\)，我们有 \(S^+(\omega) + S^-(\omega) = J(\omega)\)。

注意

频谱密度与两个功率谱（或两个相关函数）之间的关系不是一一对应的。如果一对函数 \(S^\pm(\omega)\) 满足条件，则它们是物理的。

\[S^-(\omega) = \mathrm e^{\beta(\omega - \mu)}\, S^+(\omega) .\]

对于相关函数，条件变为 \(C^-(t) = \mathrm e^{-\beta\mu}\, C^+(t - \mathrm i\beta)^\ast\)。为了灵活性，我们不强制要求功率谱/相关函数在这种意义上具有物理意义。

洛伦兹环境

费米子洛伦兹环境由类 LorentzianEnvironment 表示。它们的特征是具有以下形式的谱密度

\[J(\omega) = \frac{\gamma W^2}{(\omega - \omega_0)^2 + W^2} ,\]

其中 \(\gamma\) 是耦合强度，\(W\) 是光谱宽度，\(\omega_0\) 是共振频率。通常，共振频率被视为环境的化学势。

与玻色子Drude-Lorentz环境一样，相关函数的多指数近似，

\[C^\sigma(t) \approx \sum_{k=0}^{N_k} c^\sigma_k e^{- \nu^\sigma_k t} ,\]

可以使用Matsubara或Padé展开来获得。函数approx_by_matsubara和 approx_by_pade在QuTiP中实现了这些近似，产生可以使用的近似环境，例如与HEOM求解器一起使用。请注意，对于这种类型的环境，Matsubara展开非常低效，收敛速度比Padé展开慢得多。通常，至少需要\(N_k \geq 20\)才能获得良好的收敛性。

作为参考，我们在下面列出了系数和指数的值。对于松原展开，它们是

\[\begin{split}\nu^\sigma_{k} = \begin{cases} W - \mathrm i \sigma\, \omega_0 & k = 0\\ \frac{(2k - 1) \pi}{\beta} - \mathrm i \sigma\, \mu & k \geq 1\\ \end{cases} \;, \qquad c^\sigma_k = \begin{cases} \frac{\gamma W}{2} f_F[\sigma\beta(\omega_0 - \mu) + \mathrm i\, \beta W] & k = 0\\ \frac{\mathrm i \gamma W^2}{\beta} \frac{1}{[\mathrm i \sigma (\omega_0 - \mu) + (2k - 1) \pi / \beta]^2 - W^2} & k \geq 1\\ \end{cases} \;.\end{split}\]

帕德分解将费米分布近似为：

\[f_F(x) \approx f_F^{\mathrm{approx}}(x) = \frac{1}{2} - \sum_{k=0}^{N_k} \frac{2\kappa_k x}{x^2 + \epsilon_k^2}\]

其中 \(\kappa_k\) 和 \(\epsilon_k\) 是依赖于 \(N_k\) 的系数，并在 J. Chem Phys 133, “Efficient on the fly calculation of time correlation functions in computer simulations” 中定义。这种方法得出的指数

\[\begin{split}\nu^\sigma_{k} = \begin{cases} W - \mathrm i \sigma\, \omega_0 & k = 0\\ \frac{\epsilon_k}{\beta} - \mathrm i \sigma\, \mu & k \geq 1\\ \end{cases} \;, \qquad c^\sigma_k = \begin{cases} \frac{\gamma W}{2} f_F^{\mathrm{approx}}[\sigma\beta(\omega_0 - \mu) + \mathrm i\, \beta W] & k = 0\\ \frac{\mathrm i\, \kappa_k \gamma W^2}{\beta} \frac{1}{[\mathrm i\sigma(\omega_0 - \mu) + \epsilon_k / \beta]^2 - W^2} & k \geq 1\\ \end{cases} \;.\end{split}\]

多指数费米子环境

类似于玻色子情况下的ExponentialBosonicEnvironment，ExponentialFermionicEnvironment描述了费米子环境，其中相关函数由多指数分解给出，

\[C^\sigma(t) \approx \sum_{k=0}^{N_k^\sigma} c^\sigma_k e^{-\nu^\sigma_k t} .\]

与玻色子情况类似，该类允许我们自动计算与多指数相关函数对应的谱密度和功率谱。在这种情况下，它们是

\[S^\sigma(\omega) = \sum_{k=0}^{N_k^\sigma} 2\Re\Bigr[ \frac{c_k^\sigma}{\nu_k^\sigma + \mathrm i \sigma\, \omega} \Bigr]\]

并且 \(J(\omega) = S^+(\omega) + S^-(\omega)\)。