拓扑排序

这个例子演示了如何获取有向无环图（DAG）的拓扑排序。有向图的拓扑排序是基于有向边所隐含的优先级的线性排序。当且仅当图中没有任何循环时，拓扑排序才存在。在igraph中，我们可以使用igraph.GraphBase.topological_sorting()来获取顶点的拓扑排序。

import igraph as ig
import matplotlib.pyplot as plt

首先，我们生成一个有向无环图（DAG）：

g = ig.Graph(
    edges=[(0, 1), (0, 2), (1, 3), (2, 4), (4, 3), (3, 5), (4, 5)],
    directed=True,
)

我们可以立即验证这实际上是一个DAG：

assert g.is_dag

通过调用igraph.GraphBase.topological_sorting()可以很容易地计算出一个拓扑排序，该函数返回一个顶点ID的列表。如果给定的图不是有向无环图（DAG），将会发生错误。

results = g.topological_sorting(mode='out')
print('Topological sort of g (out):', *results)

Topological sort of g (out): 0 1 2 4 3 5

实际上，igraph.GraphBase.topological_sorting() 有两种模式， 'out' 和 'in'。'out' 是默认模式，从入度为0的节点开始。 相反，'in' 从出度为0的节点开始。要调用另一种模式，我们可以简单地使用：

results = g.topological_sorting(mode='in')
print('Topological sort of g (in):', *results)

Topological sort of g (in): 5 3 1 4 2 0

我们可以使用 igraph.Vertex.indegree() 来查找节点的入度。

for i in range(g.vcount()):
    print('degree of {}: {}'.format(i, g.vs[i].indegree()))

# %
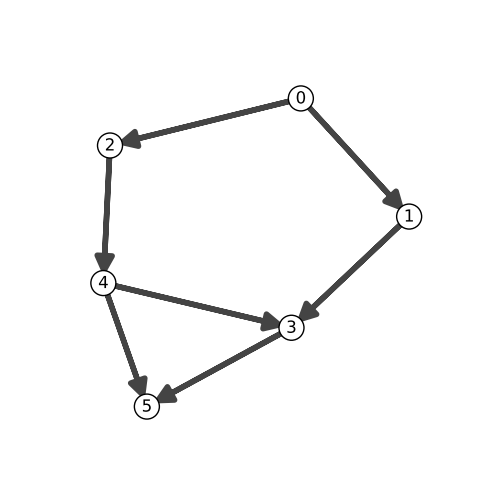
# Finally, we can plot the graph to make the situation a little clearer.
# Just to change things up a bit, we use the matplotlib visualization mode
# inspired by `xkcd <https://xkcd.com/>_:
with plt.xkcd():
    fig, ax = plt.subplots(figsize=(5, 5))
    ig.plot(
        g,
        target=ax,
        layout='kk',
        vertex_size=25,
        edge_width=4,
        vertex_label=range(g.vcount()),
        vertex_color="white",
    )

degree of 0: 0
degree of 1: 1
degree of 2: 1
degree of 3: 2
degree of 4: 1
degree of 5: 2