向量自回归 tsa.vector_ar¶
statsmodels.tsa.vector_ar 包含了一些有用的方法,用于同时对多个时间序列进行建模和分析,使用
向量自回归 (VAR) 和
向量误差修正模型 (VECM)。
VAR(p) 过程¶
我们对建模一个 \(T \times K\) 多元时间序列 \(Y\) 感兴趣,其中 \(T\) 表示观测的数量,\(K\) 表示变量的数量。估计时间序列与其滞后值之间关系的一种方法是 向量自回归过程:
其中 \(A_i\) 是一个 \(K \times K\) 系数矩阵。
我们很大程度上遵循了Lutkepohl (2005)的方法和符号,我们在这里不会详细展开。
模型拟合¶
注意
下面引用的类可以通过
statsmodels.tsa.api 模块访问。
要估计一个VAR模型,首先必须使用一个ndarray创建模型,该数组可以是同质类型或结构化类型。当使用结构化或记录数组时,类将使用传递的变量名称。否则,可以显式传递它们:
# some example data
In [1]: import numpy as np
In [2]: import pandas
In [3]: import statsmodels.api as sm
In [4]: from statsmodels.tsa.api import VAR
In [5]: mdata = sm.datasets.macrodata.load_pandas().data
# prepare the dates index
In [6]: dates = mdata[['year', 'quarter']].astype(int).astype(str)
In [7]: quarterly = dates["year"] + "Q" + dates["quarter"]
In [8]: from statsmodels.tsa.base.datetools import dates_from_str
In [9]: quarterly = dates_from_str(quarterly)
In [10]: mdata = mdata[['realgdp','realcons','realinv']]
In [11]: mdata.index = pandas.DatetimeIndex(quarterly)
In [12]: data = np.log(mdata).diff().dropna()
# make a VAR model
In [13]: model = VAR(data)
注意
类假设传递的时间序列是平稳的。非平稳或趋势数据通常可以通过一阶差分或其他方法转换为平稳数据。对于非平稳时间序列的直接分析,标准的稳定VAR(p)模型是不合适的。
要实际进行估计,请使用所需的滞后阶数调用fit方法。或者,您可以让模型根据标准信息准则(见下文)选择滞后阶数:
In [14]: results = model.fit(2)
In [15]: results.summary()
Out[15]:
Summary of Regression Results
===============================
Model: VAR
Method: OLS
Date: 三, 16, 10, 2024
Time: 18:43:21
--------------------------------------------------------------------
No. of Equations: 3.00000 BIC: -27.5830
Nobs: 200.000 HQIC: -27.7892
Log likelihood: 1962.57 FPE: 7.42129e-13
AIC: -27.9293 Det(Omega_mle): 6.69358e-13
--------------------------------------------------------------------
Results for equation realgdp
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 0.001527 0.001119 1.365 0.172
L1.realgdp -0.279435 0.169663 -1.647 0.100
L1.realcons 0.675016 0.131285 5.142 0.000
L1.realinv 0.033219 0.026194 1.268 0.205
L2.realgdp 0.008221 0.173522 0.047 0.962
L2.realcons 0.290458 0.145904 1.991 0.047
L2.realinv -0.007321 0.025786 -0.284 0.776
==============================================================================
Results for equation realcons
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const 0.005460 0.000969 5.634 0.000
L1.realgdp -0.100468 0.146924 -0.684 0.494
L1.realcons 0.268640 0.113690 2.363 0.018
L1.realinv 0.025739 0.022683 1.135 0.257
L2.realgdp -0.123174 0.150267 -0.820 0.412
L2.realcons 0.232499 0.126350 1.840 0.066
L2.realinv 0.023504 0.022330 1.053 0.293
==============================================================================
Results for equation realinv
==============================================================================
coefficient std. error t-stat prob
------------------------------------------------------------------------------
const -0.023903 0.005863 -4.077 0.000
L1.realgdp -1.970974 0.888892 -2.217 0.027
L1.realcons 4.414162 0.687825 6.418 0.000
L1.realinv 0.225479 0.137234 1.643 0.100
L2.realgdp 0.380786 0.909114 0.419 0.675
L2.realcons 0.800281 0.764416 1.047 0.295
L2.realinv -0.124079 0.135098 -0.918 0.358
==============================================================================
Correlation matrix of residuals
realgdp realcons realinv
realgdp 1.000000 0.603316 0.750722
realcons 0.603316 1.000000 0.131951
realinv 0.750722 0.131951 1.000000
使用matplotlib可视化数据的几种方法可用。
绘制输入时间序列:
In [16]: results.plot()
Out[16]: <Figure size 1000x1000 with 3 Axes>

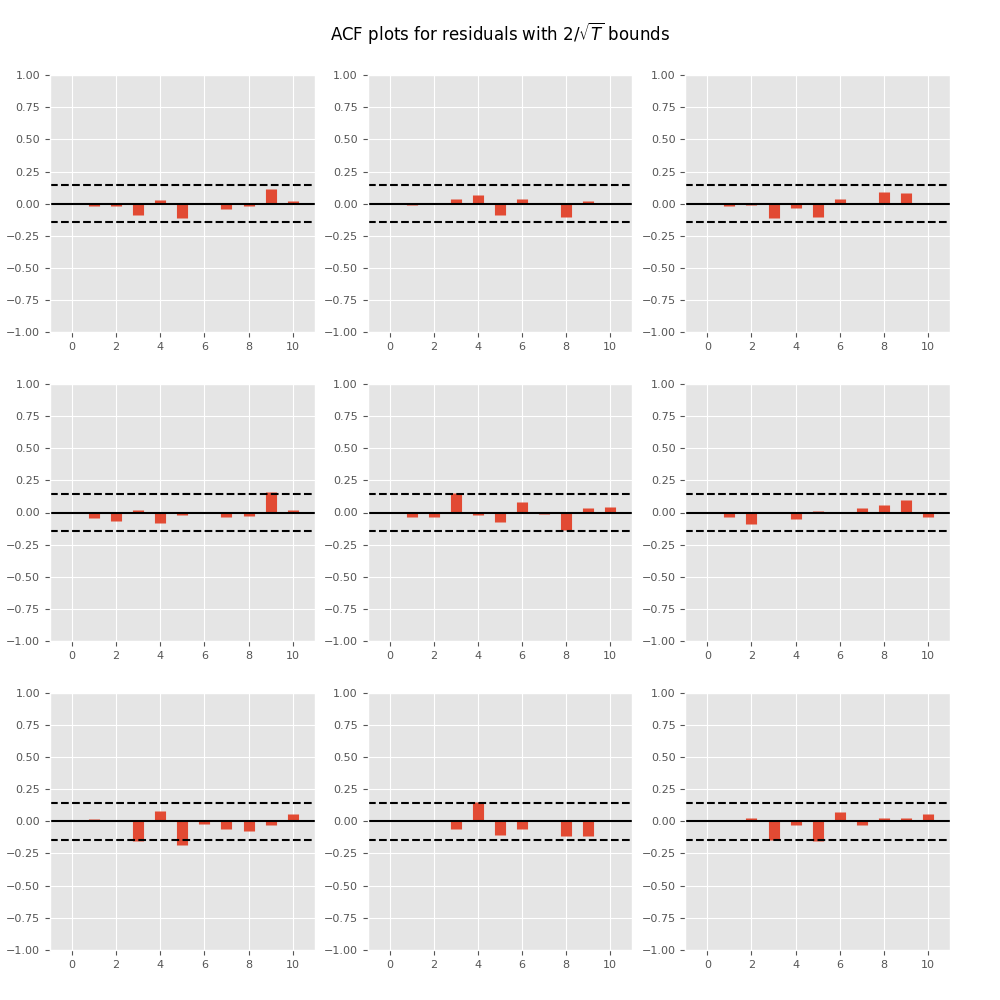
绘制时间序列自相关函数:
In [17]: results.plot_acorr()
Out[17]: <Figure size 1000x1000 with 9 Axes>
滞后阶数选择¶
滞后阶数的选择可能是一个困难的问题。标准分析采用似然检验或基于信息准则的阶数选择。我们实现了后者,可通过VAR类访问:
In [18]: model.select_order(15)
Out[18]: <statsmodels.tsa.vector_ar.var_model.LagOrderResults at 0x3262e80d0>
当调用fit函数时,可以传递最大滞后数和用于顺序选择的顺序标准:
In [19]: results = model.fit(maxlags=15, ic='aic')
预测¶
线性预测器是均方误差意义下的最优h步前向预测:
我们可以使用forecast函数来生成这个预测。请注意,我们必须为预测指定“初始值”:
In [20]: lag_order = results.k_ar
In [21]: results.forecast(data.values[-lag_order:], 5)
Out[21]:
array([[ 0.0062, 0.005 , 0.0092],
[ 0.0043, 0.0034, -0.0024],
[ 0.0042, 0.0071, -0.0119],
[ 0.0056, 0.0064, 0.0015],
[ 0.0063, 0.0067, 0.0038]])
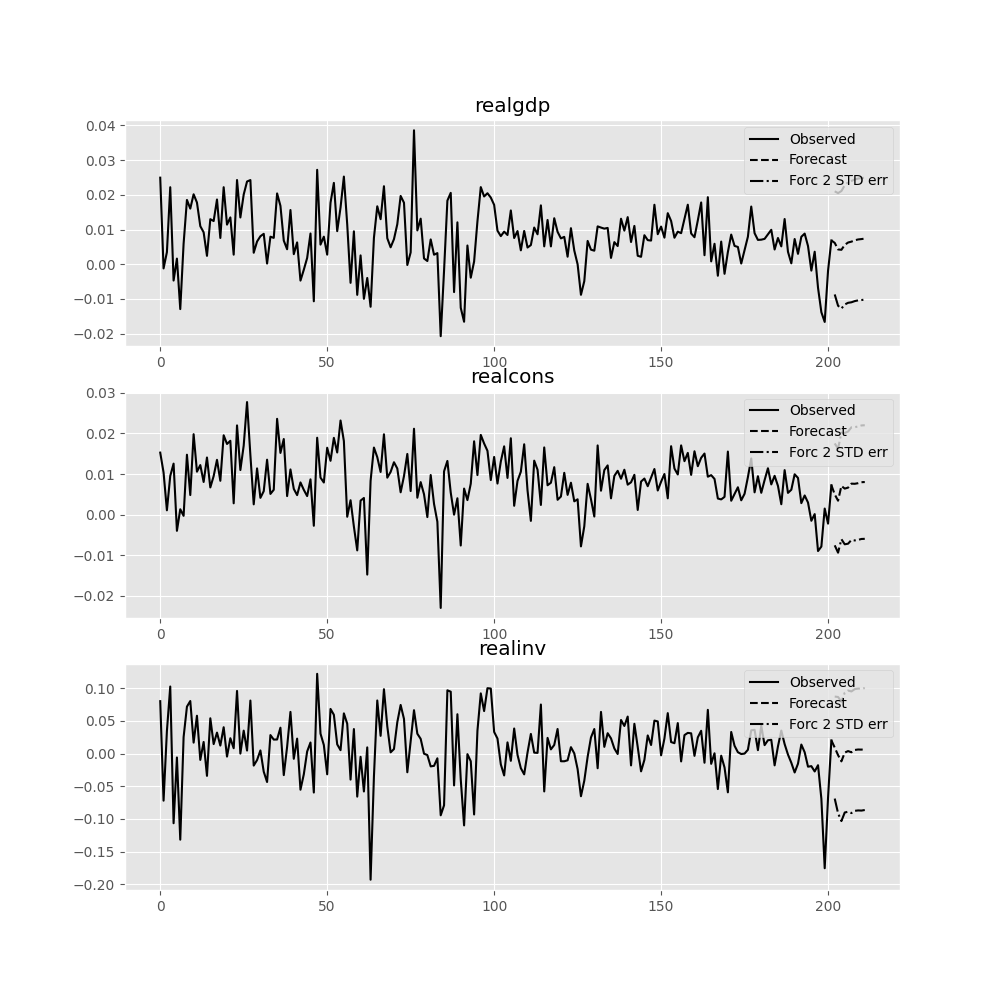
函数 forecast_interval 将生成上述预测以及渐近标准误差。这些可以使用函数 plot_forecast 进行可视化:
In [22]: results.plot_forecast(10)
Out[22]: <Figure size 1000x1000 with 3 Axes>
类参考¶
|
拟合 VAR(p) 过程并进行滞后阶数选择 |
|
类表示一个已知的VAR(p)过程 |
|
使用固定滞后阶数估计VAR(p)过程 |
估计后分析¶
在估计之后,向量自回归过程的几个过程属性和附加结果是可用的。
|
用于选择模型滞后阶数的结果类。 |
|
假设检验的结果类。 |
|
Jarque-Bera 非正态性检验结果类。 |
|
Portmanteau-test 残差自相关检验的结果类。 |
脉冲响应分析¶
脉冲响应在计量经济学研究中具有重要意义:它们是某个变量中单位脉冲的估计响应。在实际应用中,它们是通过VAR(p)过程的MA(\(\infty\))表示来计算的:
我们可以通过在VARResults对象上调用irf函数来执行脉冲响应分析:
In [23]: irf = results.irf(10)
这些可以使用plot函数以正交化或非正交化的形式进行可视化。默认情况下,渐近标准误差在95%显著性水平上绘制,用户可以进行修改。
注意
正交化是通过对估计误差协方差矩阵 \(\hat \Sigma_u\) 的 Cholesky 分解完成的,因此解释可能会根据变量顺序的变化而变化。
In [24]: irf.plot(orth=False)
Out[24]: <Figure size 1000x1000 with 9 Axes>
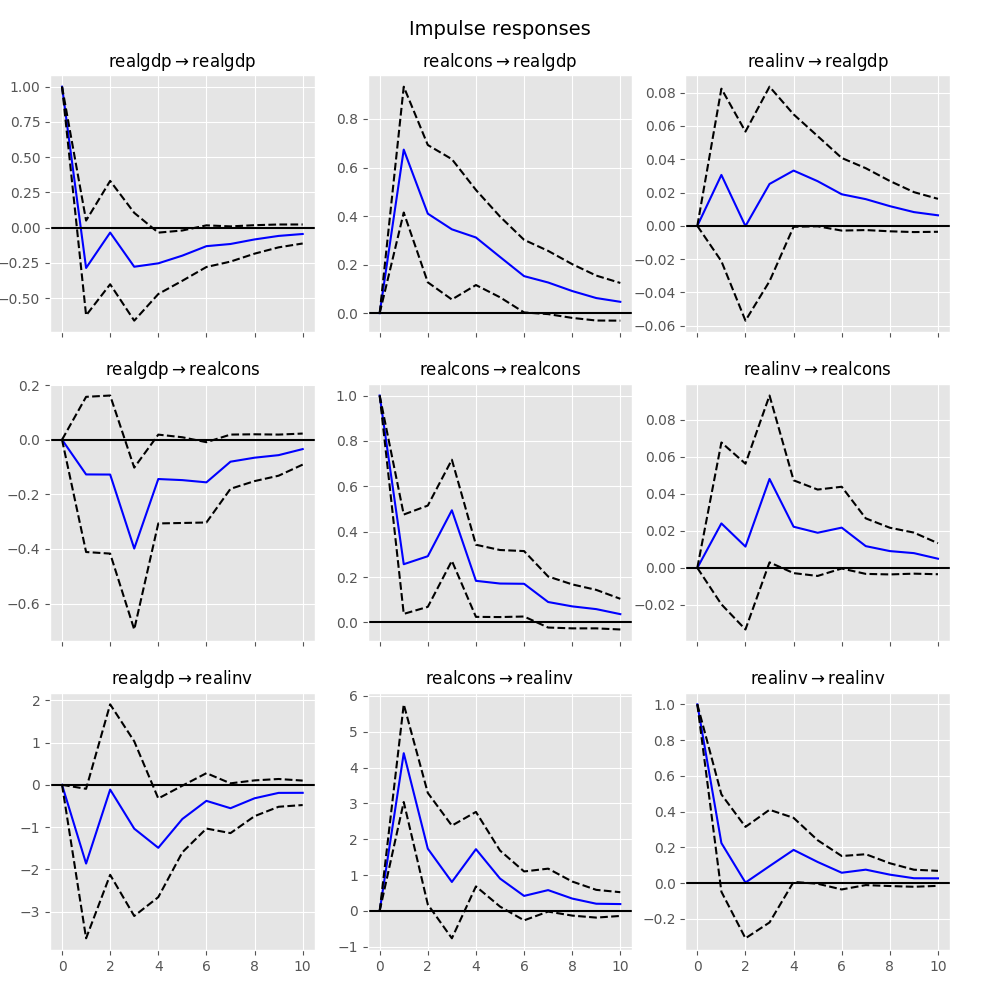
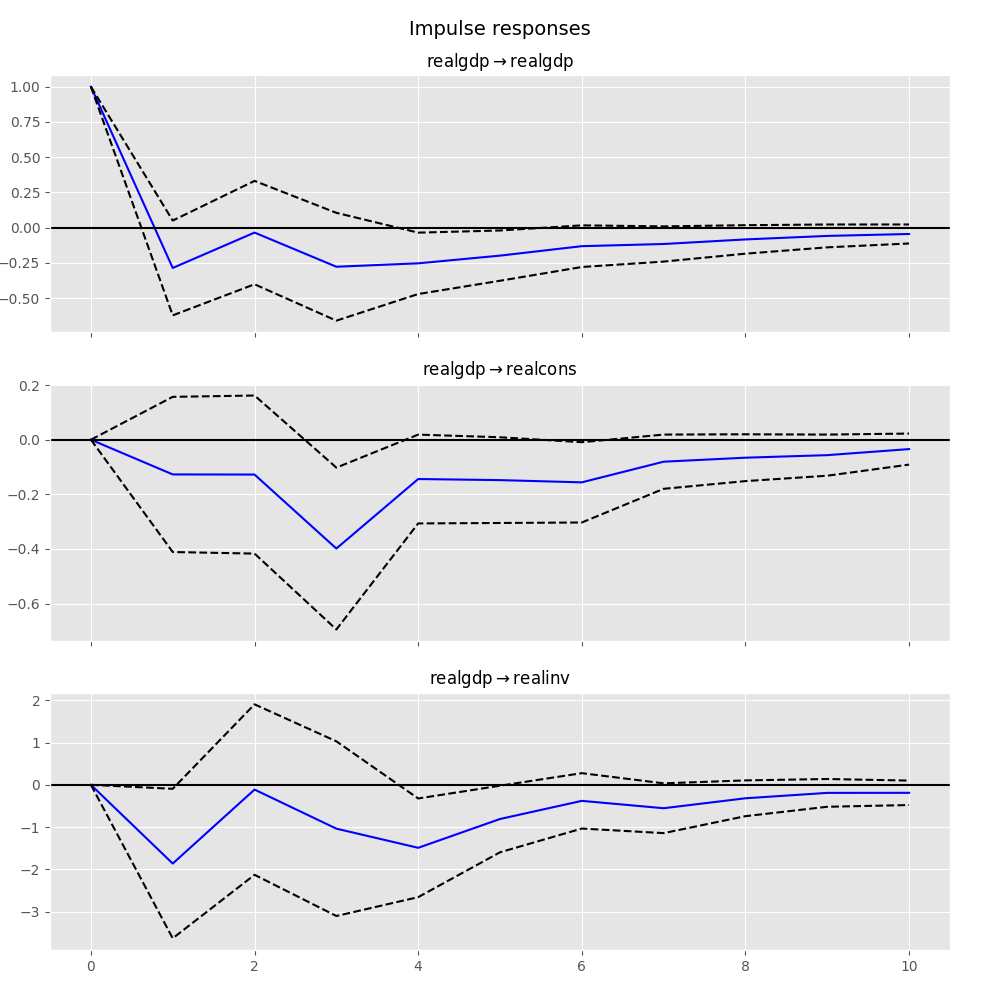
注意,plot 函数是灵活的,如果需要,可以仅绘制感兴趣的变量:
In [25]: irf.plot(impulse='realgdp')
Out[25]: <Figure size 1000x1000 with 3 Axes>
累积效应 \(\Psi_n = \sum_{i=0}^n \Phi_i\) 可以通过长期效应绘制如下:
In [26]: irf.plot_cum_effects(orth=False)
Out[26]: <Figure size 1000x1000 with 9 Axes>

|
脉冲响应分析类。 |
预测误差方差分解 (FEVD)¶
在i步提前预测中,组件j在k上的预测误差可以使用正交化的脉冲响应\(\Theta_i\)进行分解:
这些是通过 fevd 函数计算的,直到总步数之前:
In [27]: fevd = results.fevd(5)
In [28]: fevd.summary()
FEVD for realgdp
realgdp realcons realinv
0 1.000000 0.000000 0.000000
1 0.864889 0.129253 0.005858
2 0.816725 0.177898 0.005378
3 0.793647 0.197590 0.008763
4 0.777279 0.208127 0.014594
FEVD for realcons
realgdp realcons realinv
0 0.359877 0.640123 0.000000
1 0.358767 0.635420 0.005813
2 0.348044 0.645138 0.006817
3 0.319913 0.653609 0.026478
4 0.317407 0.652180 0.030414
FEVD for realinv
realgdp realcons realinv
0 0.577021 0.152783 0.270196
1 0.488158 0.293622 0.218220
2 0.478727 0.314398 0.206874
3 0.477182 0.315564 0.207254
4 0.466741 0.324135 0.209124
它们也可以通过返回的 FEVD 对象进行可视化:
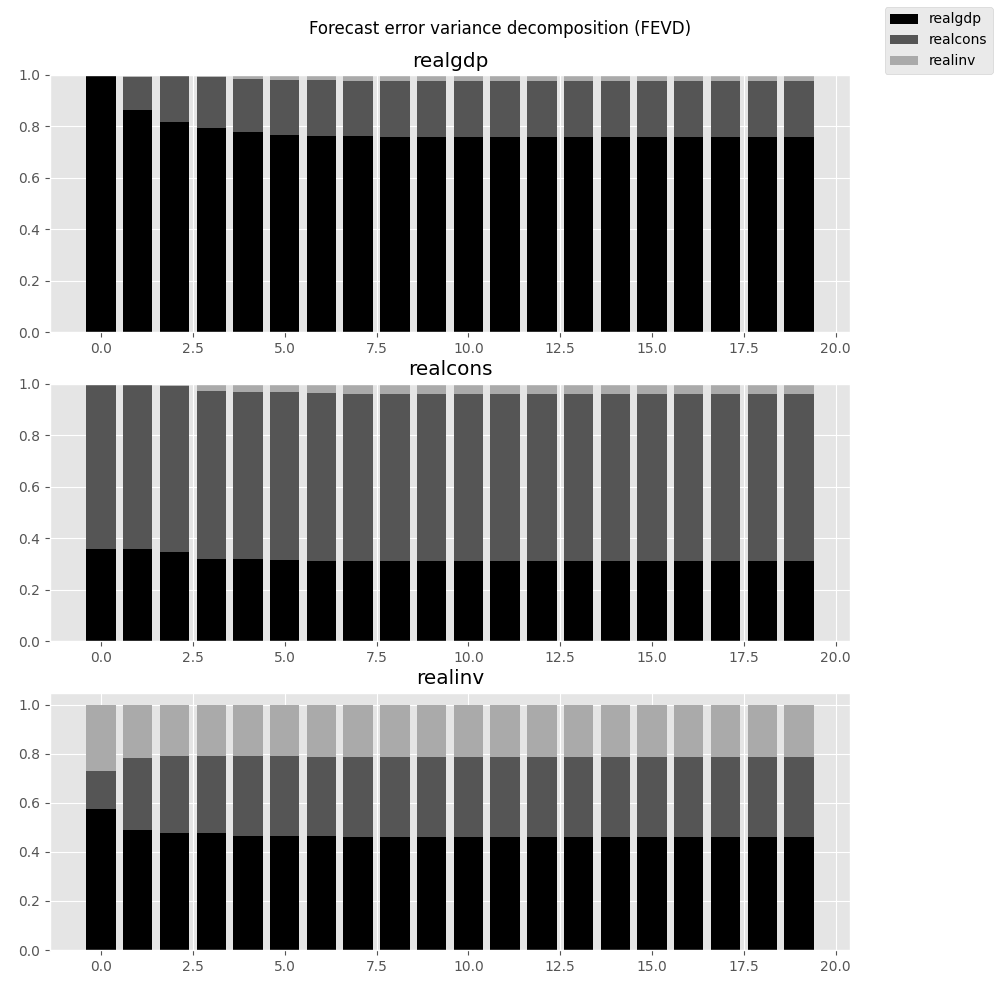
In [29]: results.fevd(20).plot()
Out[29]: <Figure size 1000x1000 with 3 Axes>
|
计算并绘制预测误差方差分解和渐近标准误差 |
统计测试¶
提供了多种不同的方法来执行关于模型结果的假设检验,以及模型假设的有效性(正态性、误差的白色性/“独立同分布性”等)。
格兰杰因果关系¶
人们通常对一个变量或一组变量是否对另一个变量具有“因果性”感兴趣,这里的“因果性”是基于某种定义的。在VAR模型的背景下,可以说一组变量在其中一个VAR方程中具有格兰杰因果性。我们不会详细讨论格兰杰因果性的数学或定义,而是留给读者自行了解。VARResults对象具有test_causality方法,用于执行Wald(\(\chi^2\))检验或F检验。
In [30]: results.test_causality('realgdp', ['realinv', 'realcons'], kind='f')
Out[30]: <statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults at 0x3268802d0>
正态性¶
正如本文档开头所指出的,白噪声分量
\(u_t\) 假设为正态分布。虽然这一假设
对于参数估计的一致性或渐近正态性并非必需,但在有限样本中,当残差为高斯白噪声时,结果通常更为可靠。为了测试这一假设是否与
数据集一致,VARResults 提供了 test_normality 方法。
In [31]: results.test_normality()
Out[31]: <statsmodels.tsa.vector_ar.hypothesis_test_results.NormalityTestResults at 0x326204d10>
残差的白色性¶
要测试估计残差的白色度(这意味着不存在显著的残差自相关),可以使用VARResults的test_whiteness方法。
|
假设检验的结果类。 |
|
Granger因果关系和瞬时因果关系的结果类。 |
|
Jarque-Bera 非正态性检验结果类。 |
|
Portmanteau-test 残差自相关检验的结果类。 |
结构向量自回归¶
有一组匹配的类,用于处理某些类型的结构向量自回归模型。
|
拟合 VAR 然后估计 A 和 B 的结构成分,定义如下: |
|
类表示一个已知的SVAR(p)过程 |
|
使用固定滞后阶数估计VAR(p)过程 |
向量误差修正模型 (VECM)¶
向量误差修正模型用于研究短期偏离一个或多个永久性随机趋势(单位根)的情况。VECM通过施加由假设的随机趋势数量所隐含的结构来建模时间序列向量的差分。VECM用于指定和估计这些模型。
一个VECM(\(k_{ar}-1\))具有以下形式
哪里
如[1]第7章所述。
一个带有确定性项的VECM(\(k_{ar} - 1\))的形式为
在 \(D^{co}_{t-1}\) 中,我们有确定性项,这些项位于协整关系内(或被限制在协整关系内)。
\(\eta\) 是对应的估计量。要将确定性项传递到协整关系内,我们可以使用 exog_coint 参数。
对于截距和线性趋势这两种特殊情况,存在一种更简单的声明这些项的方法:我们可以分别将 "ci" 和 "li"
传递给 deterministic 参数。因此,对于协整关系内的截距,我们可以将 "ci" 作为 deterministic
传递,或者如果 data 作为 endog 参数传递,则将 np.ones(len(data)) 作为 exog_coint 传递。
这确保了对于所有 \(t\),\(D_{t-1}^{co} = 1\)。
我们也可以在协整关系之外使用确定性项。
这些在上述公式中定义为 \(D_t\),并在矩阵 \(C\) 中对应估计量。我们通过将这些项传递给 exog 参数来指定它们。对于截距和/或线性趋势,我们再次可以选择使用 deterministic。对于截距,我们传递 "co",对于线性趋势,我们传递 "lo",其中 o 代表 outside。
下表显示了[2]中考虑的五种情况。最后一列指示了在这些情况下应传递给deterministic参数的字符串。
案例 |
截距 |
线性趋势的斜率 |
确定性 |
|---|---|---|---|
我 |
0 |
0 |
|
第二部分 |
\(- \alpha \beta^T \mu\) |
0 |
|
三 |
\(\neq 0\) |
0 |
|
第四部分 |
\(\neq 0\) |
\(- \alpha \beta^T \gamma\) |
|
V |
\(\neq 0\) |
\(\neq 0\) |
|
|
表示向量误差修正模型(VECM)的类。 |
|
Johansen协整检验,用于确定VECM的协整秩 |
|
Johansen协整检验的结果类 |
|
基于每个可用的信息准则计算滞后阶数选择。 |
|
计算VECM的协整秩。 |
|
用于保存向量误差修正模型(VECM)相关估计结果的类。 |
|
用于保存协整秩测试结果的类。 |