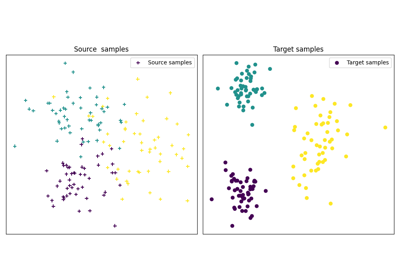
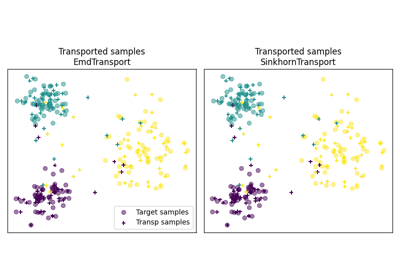
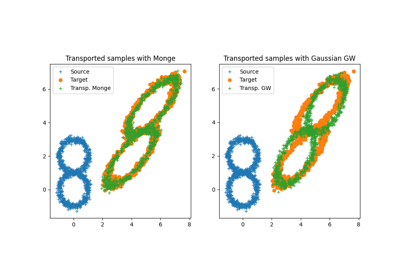
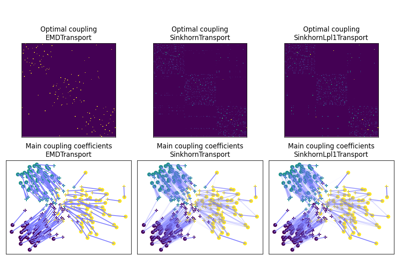
ot.da
通过最优传输进行领域适应
函数
- ot.da.distribution_estimation_uniform(X)[源]
从样本数组中估算一个均匀分布 \(\mathbf{X}\)
- Parameters:
X (类似数组, 形状 (样本数量, 特征数量)) – 样本数组
- Returns:
mu – 从 \(\mathbf{X}\) 估计的均匀分布
- Return type:
类似数组,形状为 (n_samples,)
- ot.da.emd_laplace(a, b, xs, xt, M, sim='knn', sim_param=None, reg='pos', eta=1, alpha=0.5, numItermax=100, stopThr=1e-09, numInnerItermax=100000, stopInnerThr=1e-09, log=False, verbose=False)[源]
解决带有拉普拉斯正则化的最优传输问题(OT)
\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \eta \cdot \Omega_\alpha(\gamma)\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]其中:
\(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重(总和为1)
\(\mathbf{x_s}\) 和 \(\mathbf{x_t}\) 是源样本和目标样本
\(\mathbf{M}\) 是 (ns, nt) 计量成本矩阵
\(\Omega_\alpha\) 是拉普拉斯正则化项
\[\Omega_\alpha = \frac{1 - \alpha}{n_s^2} \sum_{i,j} \mathbf{S^s}_{i,j} \|T(\mathbf{x}^s_i) - T(\mathbf{x}^s_j) \|^2 + \frac{\alpha}{n_t^2} \sum_{i,j} \mathbf{S^t}_{i,j} \|T(\mathbf{x}^t_i) - T(\mathbf{x}^t_j) \|^2\]其中 \(\mathbf{S^s}_{i,j}, \mathbf{S^t}_{i,j}\) 表示源和目标相似性矩阵,\(T(\cdot)\) 是一个重心映射。
用于解决该问题的算法是条件梯度算法,如[5]中提出的。
- Parameters:
a (类数组 (ns,)) – 源域中的样本权重
b (类数组 (nt,)) – 目标领域中的样本权重
xs (类似数组 (ns,d)) – 源领域中的样本
xt (类数组 (nt,d)) – 目标领域中的样本
M (数组-like (ns,nt)) – 损失矩阵
sim (string, optional) – 相似度的类型(‘knn’ 或 ‘gauss’),用于构建拉普拉斯算子。
sim_param (int 或 float, 可选) – 参数(用于计算拉普拉斯算子时,sim=’knn’的最近邻数量或sim=’gauss’的带宽)。
reg (string) – 拉普拉斯正则化的类型
eta (float) – 拉普拉斯正则化的正则化项
alpha (float) – 源域在正则化中的重要性正则化项
numItermax (int, 可选) – 最大迭代次数
stopThr (float, 可选) – 错误停止阈值(内部 emd 求解器)(>0)
numInnerItermax (int, 可选) – 最大迭代次数(内层CG求解器)
stopInnerThr (float, 可选) – 错误的停止阈值(内部CG求解器) (>0)
verbose (bool, 可选) – 在迭代过程中打印信息
log (bool, 可选) – 如果为真,则记录日志
- Returns:
gamma ((ns, nt) 类数组) – 给定参数的最优运输矩阵
log (字典) – 仅当参数中的 log==True 时返回日志字典
参考文献
另请参见
ot.lp.emd未正则化的OT
ot.optim.cg通用正则化OT
- ot.da.sinkhorn_l1l2_gl(a, labels_a, b, M, reg, eta=0.1, numItermax=10, numInnerItermax=200, stopInnerThr=1e-09, eps=1e-12, verbose=False, log=False)[源]
解决带有群体套索正则化的熵正则化最优传输问题
该函数解决以下优化问题:
\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \mathrm{reg} \cdot \Omega_e(\gamma) + \eta \ \Omega_g(\gamma)\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]其中 :
\(\mathbf{M}\) 是 (ns, nt) 计量成本矩阵
\(\Omega_e\) 是熵正则化项 \(\Omega_e(\gamma)=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)
\(\Omega_g\) 是组套索正则化项 \(\Omega_g(\gamma)=\sum_{i,c} \|\gamma_{i,\mathcal{I}_c}\|^2\) 其中 \(\mathcal{I}_c\) 是源域中类别c的样本索引。
\(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重(总和为1)
用于解决该问题的算法是广义条件梯度,如[5, 7]中所提出的。
- Parameters:
a (类数组 (ns,)) – 源域中的样本权重
labels_a (类似数组 (ns,)) – 源域中样本的标签
b (类数组 (nt,)) – 目标域中的样本
M (数组-like (ns,nt)) – 损失矩阵
reg (float) – 熵正则化的正则化项 >0
eta (float, 可选) – 组套索正则化的正则化项 >0
numItermax (int, 可选) – 最大迭代次数
numInnerItermax (int, 可选) – 最大迭代次数(内部Sinkhorn求解器)
stopInnerThr (float, 可选) – 错误的停止阈值(内部Sinkhorn求解器) (>0)
eps (float, 可选 (默认=1e-12)) – 避免除以零的小值
verbose (bool, 可选) – 在迭代过程中打印信息
log (bool, 可选) – 如果为真,则记录日志
- Returns:
gamma ((ns, nt) 类数组) – 给定参数的最优运输矩阵
log (字典) – 仅当参数中的 log==True 时返回日志字典
参考文献
[5] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[7] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
另请参见
ot.optim.gcgOT 问题的一般条件梯度
- ot.da.sinkhorn_lpl1_mm(a, labels_a, b, M, reg, eta=0.1, numItermax=10, numInnerItermax=200, stopInnerThr=1e-09, verbose=False, log=False)[源]
解决具有非凸组lasso正则化的熵正则化最优传输问题
该函数解决以下优化问题:
\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \mathrm{reg} \cdot \Omega_e(\gamma) + \eta \ \Omega_g(\gamma)\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]其中 :
\(\mathbf{M}\) 是 (ns, nt) 计量成本矩阵
\(\Omega_e\) 是熵正则化项 \(\Omega_e (\gamma)=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)
\(\Omega_g\) 是组lasso正则化项 \(\Omega_g(\gamma)=\sum_{i,c} \|\gamma_{i,\mathcal{I}_c}\|^{1/2}_1\) 其中 \(\mathcal{I}_c\) 是源域中来自类 c 的样本索引。
\(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重(总和为1)
用于解决问题的算法是广义条件梯度,如[5, 7]中提出的。
- Parameters:
a (类数组 (ns,)) – 源域中的样本权重
labels_a (类似数组 (ns,)) – 源域中样本的标签
b (类数组 (nt,)) – 目标领域中的样本权重
M (数组-like (ns,nt)) – 损失矩阵
reg (float) – 熵正则化的正则化项 >0
eta (float, 可选) – 组套索正则化的正则化项 >0
numItermax (int, 可选) – 最大迭代次数
numInnerItermax (int, 可选) – 最大迭代次数(内部Sinkhorn求解器)
stopInnerThr (float, 可选) – 错误的停止阈值(内部Sinkhorn求解器) (>0)
verbose (bool, 可选) – 在迭代过程中打印信息
log (bool, 可选) – 如果为真,则记录日志
- Returns:
gamma ((ns, nt) 类数组) – 给定参数的最优运输矩阵
log (字典) – 仅当参数中的 log==True 时返回日志字典
参考文献
[5] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “用于领域适应的最优传输,”发表于IEEE 模式分析与机器智能学报, 第PP卷,第99期,页码1-1
[7] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
另请参见
ot.lp.emd未正则化的OT
ot.bregman.sinkhorn熵正则化最优传输
ot.optim.cg通用正则化OT
类
- class ot.da.BaseTransport[源]
OTDA对象的基类
注意
所有估计器应在其
__init__中将所有可以在类级别设置的参数指定为显式关键字参数(不使用*args或**kwargs)。fit 方法应该:
估计一个成本矩阵并将其存储在cost_属性中
估计耦合矩阵并将其存储在coupling_属性中
从源数据和目标数据估计分布,并将它们存储在 mu_s 和 mu_t 属性中
将 Xs 和 Xt 存储在属性中,以便在 transform 和 inverse_transform 方法中稍后使用
transform 方法应该始终接收一个 Xs 参数作为输入
inverse_transform 方法应该始终接收一个 Xt 参数作为输入
transform_labels 方法应该始终接收一个 ys 参数作为输入
inverse_transform_labels 方法应该始终接收一个 yt 参数作为输入
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 训练类标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- fit_transform(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建一个耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\) 并将源样本 \(\mathbf{X_s}\) 转换到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 训练样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
transp_Xs – 源样本样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- inverse_transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将目标样本 \(\mathbf{X_t}\) 转移到源样本 \(\mathbf{X_s}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (类数组, 形状 (n_target_samples,)) –
目标类标签。如果某些目标样本未标记,则用 -1 填充 \(\mathbf{y_t}\) 的元素。
警告:请注意,由于这种约定,-1 不能被用作 类标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xt – 被传输的目标样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- inverse_transform_labels(yt=None)[源]
传播目标标签 \(\mathbf{y_t}\) 以获取估计的源标签 \(\mathbf{y_s}\)
- Parameters:
yt (类数组, 形状 (n_target_samples,))
- Returns:
transp_ys – 估算的软源标签。
- Return type:
类数组,形状 (n_source_samples, nb_classes)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (数组类型, 形状 (n_target_samples,)) –
目标的类标签。如果某些目标样本没有标签,将 \(\mathbf{y_t}\)的元素填充为 -1。
警告:请注意,由于这个约定,-1不能用作类标签。
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xs – 运输源样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- transform_labels(ys=None)[源]
传播源标签 \(\mathbf{y_s}\) 以获得估计的目标标签,如在 [27] 中所示。
- Parameters:
ys (类似数组, 形状 (n_source_samples,)) – 源类标签
- Returns:
transp_ys – 估计的软目标标签。
- Return type:
类似数组,形状 (n_target_samples, nb_classes)
参考文献
[27] Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia “在目标偏移下的多源领域适应的最优传输”, 国际人工智能与统计会议 (AISTATS), 2019.
使用 ot.da.BaseTransport 的示例
- class ot.da.EMDLaplaceTransport(reg_type='pos', reg_lap=1.0, reg_src=1.0, metric='sqeuclidean', norm=None, similarity='knn', similarity_param=None, max_iter=100, tol=1e-09, max_inner_iter=100000, inner_tol=1e-09, log=False, verbose=False, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans')[源]
基于地球移动者距离的领域适应OT方法,带拉普拉斯正则化
- Parameters:
reg_type (字符串 可选 (默认='pos')) – 正则化项的类型:‘pos’和‘disp’分别对应于在 [2] 和 [6] 中定义的正则化项。
reg_lap (float, 可选 (默认=1)) – 拉普拉斯正则化参数
reg_src (float, 可选 (默认=0.5)) – 正规化中的源相对重要性
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
相似度 (字符串, 可选的 (默认="knn")) – 使用的相似度,可以是knn或高斯
similarity_param (int 或 float, 可选 (默认=None)) – 相似度参数:最近邻的数量或带宽 如果相似度为“knn”或“gaussian”,分别。如果提供了None, 则分别设置为3或平均成对平方欧几里得距离。
max_iter (int, 可选 (默认=100)) – BCD迭代的最大次数
tol (float, 可选 (默认=1e-5)) – 相对损失减少的停止阈值 (>0)
max_inner_iter (int, 可选 (默认=10)) – 最大迭代次数(内部CG求解器)
inner_tol (float, 可选 (默认=1e-6)) – 停止阈值在误差上 (内层CG求解器) (>0)
log (int, 可选 (默认=False)) – 控制优化算法的日志
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[2] R. Flamary, N. Courty, D. Tuia, A. Rakotomamonjy, “带有拉普拉斯正则化的最优传输:应用于领域适应和形状匹配,” 在NIPS关于最优传输和机器学习OTML的研讨会,2014。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化离散最优传输. SIAM 图像科学期刊, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
使用 ot.da.EMDLaplaceTransport 的示例
- class ot.da.EMDTransport(metric='sqeuclidean', norm=None, log=False, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=10, max_iter=100000)[源]
基于地球移动者距离的领域适应OT方法
- Parameters:
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
log (int, 可选 (默认=False)) – 控制优化算法的日志
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=10)) – 控制半监督模式。不同类别的标记源样本与目标样本之间的传输将表现出无限成本 (是成本矩阵最大值的10倍)
max_iter (int, 可选 (默认=100000)) – 在优化算法尚未收敛时,停止优化前的最大迭代次数。
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
使用ot.da.EMDTransport的示例
- class ot.da.JCPOTTransport(reg_e=0.1, max_iter=10, tol=1e-08, verbose=False, log=False, metric='sqeuclidean', out_of_sample_map='ferradans')[源]
基于Wasserstein重心算法的多源目标偏移域适应OT方法。
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (bool, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
- coupling_
每个源域与目标域之间的最优配对集
- Type:
形状为 K x (n_source_samples, n_target_samples) 的类数组对象列表
- proportions_
目标领域中的估计类别比例
- Type:
类数组,形状为 (n_classes,)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia “针对目标偏移的多源领域适应的最优传输”, 国际人工智能与统计会议(AISTATS), 第89卷,页849-858,2019年。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本和目标样本集的列表构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
- Returns:
self – 返回自我。
- Return type:
- inverse_transform_labels(yt=None)[源]
传播目标标签 \(\mathbf{y_t}\) 以获取估计的源标签 \(\mathbf{y_s}\)
- Parameters:
yt (数组类似, 形状 (n_target_samples,)) – 目标类别标签
- Returns:
transp_ys – 估计的软源标签列表
- Return type:
K个类数组对象的列表,形状为 K x (nk_source_samples, nb_classes)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (列表 包含 K 个类似数组的对象, 形状为 K x (nk_source_samples, n_features)) – 训练输入样本的列表。
ys (列表 of K 类似数组的对象, 形状 K x (nk_source_samples,)) – 标签的列表
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- transform_labels(ys=None)[源]
传播源标签 \(\mathbf{y_s}\) 以获得目标标签,如在 [27]
- Parameters:
ys (list 的 K 类数组对象, 形状 K x (nk_source_samples,)) – 类别标签的列表
- Returns:
yt – 估计的软目标标签。
- Return type:
类似数组,形状 (n_target_samples, nb_classes)
参考文献
[27] Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia “在目标偏移下的多源领域适应的最优传输”, 国际人工智能与统计会议 (AISTATS), 2019.
使用 ot.da.JCPOTTransport 的示例
- class ot.da.LinearGWTransport(log=False, sign_eigs=None, distribution_estimation=<function distribution_estimation_uniform>)[源]
经验分布之间的OT高斯Gromov-Wasserstein线性算子
该函数估计最佳线性算子,以便在Gromov-Wasserstein距离上最佳地对齐两个经验分布。这相当于估计两个高斯分布之间的闭式映射 \(\mathcal{N}(\mu_s,\Sigma_s)\) 和 \(\mathcal{N}(\mu_t,\Sigma_t)\),正如在[57]中提出的。
从源到目标的线性算子 \(M\)
\[M(\mathbf{x})= \mathbf{A} \mathbf{x} + \mathbf{b}\]其中矩阵 \(\mathbf{A}\) 和向量 \(\mathbf{b}\) 在 [57] 中定义。
- Parameters:
参考文献
[57] Delon, J., Desolneux, A., & Salmona, A. (2022). Gromov–Wasserstein 高斯分布之间的距离。应用概率杂志, 59(4), 1178-1198。
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
使用 ot.da.LinearGWTransport 的示例
- class ot.da.LinearTransport(reg=1e-08, bias=True, log=False, distribution_estimation=<function distribution_estimation_uniform>)[源]
经验分布之间的OT线性算子
该函数估计了最佳线性算子,以对齐两个经验分布。这相当于估计两个高斯分布之间的闭合形式映射 \(\mathcal{N}(\mu_s,\Sigma_s)\) 和 \(\mathcal{N}(\mu_t,\Sigma_t)\),如在 [14] 中提出,并在 [15] 的备注2.29中讨论。
从源到目标的线性算子 \(M\)
\[M(\mathbf{x})= \mathbf{A} \mathbf{x} + \mathbf{b}\]其中 :
\[ \begin{align}\begin{aligned}\mathbf{A} &= \Sigma_s^{-1/2} \left(\Sigma_s^{1/2}\Sigma_t\Sigma_s^{1/2} \right)^{1/2} \Sigma_s^{-1/2}\\\mathbf{b} &= \mu_t - \mathbf{A} \mu_s\end{aligned}\end{align} \]- Parameters:
参考文献
[14] Knott, M. 和 Smith, C. S. “关于分布的最优映射”,优化理论与应用期刊 第43卷,1984年
[15] Peyré, G., & Cuturi, M. (2017). “计算最优运输”, 2018.
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- inverse_transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将目标样本 \(\mathbf{X_t}\) 转移到源样本 \(\mathbf{X_s}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xt – 被传输的目标样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xs – 运输源样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
使用 ot.da.LinearTransport 的示例
- class ot.da.MappingTransport(mu=1, eta=0.001, bias=False, metric='sqeuclidean', norm=None, kernel='linear', sigma=1, max_iter=100, tol=1e-05, max_inner_iter=10, inner_tol=1e-06, log=False, verbose=False, verbose2=False)[源]
MappingTransport:旨在联合估计最优传输耦合及相关映射的DA方法
- Parameters:
mu (float, 可选 (默认=1)) – 线性OT损失的权重 (>0)
eta (float, 可选 (默认=0.001)) – 线性映射 L 的正则化项 (>0)
偏差 (布尔值, 可选的 (默认=False)) – 估计具有恒定偏差的线性映射
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
核函数 (字符串, 可选 (默认="线性")) – 使用的核函数可以是线性或高斯
sigma (float, 可选 (默认=1)) – 高斯核参数
max_iter (int, 可选 (默认=100)) – BCD迭代的最大次数
tol (float, 可选 (默认=1e-5)) – 相对损失减少的停止阈值 (>0)
max_inner_iter (int, 可选 (默认=10)) – 最大迭代次数(内部CG求解器)
inner_tol (float, 可选 (默认=1e-6)) – 停止阈值在误差上 (内层CG求解器) (>0)
log (bool, 可选 (默认为False)) – 如果为True,则记录日志
verbose (bool, 可选 (默认=False)) – 在迭代过程中打印信息
verbose2 (bool, 可选 (默认=False)) – 在迭代过程中打印信息
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- mapping_
相关映射
数组类型,形状 (n_features (+ 1), n_features), (如果有偏差)当核函数为线性时
类数组,形状 (n_source_samples (+ 1), n_features), (如果有偏置) 当核 == 高斯时
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[8] M. Perrot, N. Courty, R. Flamary, A. Habrard, “离散最优传输的映射估计”, 神经信息处理系统 (NIPS), 2016.
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
构建最佳耦合并估计来自源样本和目标样本集的相关映射 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自身
- Return type:
使用 ot.da.MappingTransport 的示例
- class ot.da.NearestBrenierPotential(strongly_convex_constant=0.6, gradient_lipschitz_constant=1.4, log=False, its=100, seed=None)[源]
光滑强凸最近Brenier势 (SSNB) 是一种来自 [58] 的方法,它计算具有L-利普希茨梯度的l-强凸势 \(\varphi\),使得 \(\nabla \varphi \# \mu \approx \nu\)。这种规则性只能在环境空间的一个划分的分量上被强加(由点类编码),这相比于强制全局规则性是一种放松。
SSNBs通过解决优化问题来接近目标度量:
\begin{gather*} \varphi \in \text{argmin}_{\varphi \in \mathcal{F}}\ \text{W}_2(\nabla \varphi \#\mu_s, \mu_t), \end{gather*}其中 \(\mathcal{F}\) 是在每个集合 \(E_k\) l-强凸的空间函数,具有L-Lipschitz梯度,给定 \((E_k)_{k \in [K]}\) 是环境源空间的一个划分。
该问题通过“拟合”源数据和目标数据来解决,使用凸二次约束二次规划,得到值
phi和源点处的梯度G。然后,通过在每个点上解决(更简单的)二次约束线性规划,使用拟合“参数”phi和G来找到“新”源样本的图像。我们提供了两种可能的图像,分别对应于“下限”和“上限势”([59], 定理 3.14)。这两种图像都是SSNB问题的最优解,并可以在实践中使用。警告
此函数需要CVXPY库
警告
接受任何后端,但会首先转换为Numpy,然后再转换回后端。
- Parameters:
参考文献
[58] François-Pierre Paty, Alexandre d’Aspremont, and Marco Cuturi. 正则性作为正则化: 在最优运输中的光滑和强凸Brenier势。发表于国际人工智能与统计会议,页码 1222–1232。PMLR,2020。
[59] Adrien B Taylor. 凸插值和一阶方法在凸优化中的性能估计。博士论文,洛万大学,洛万-拉-诺夫,比利时,2017年。
另请参见
ot.mapping.nearest_brenier_potential_fit在源数据和目标数据上拟合SSNB
ot.mapping.nearest_brenier_potential_predict_bounds在新源数据上预测SSNB图像
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
将平滑强凸最近布雷尼尔势能[58]拟合到源数据
Xs到目标数据Xt,分区由(可选的)标签ys给出。用于
ot.mapping.nearest_brenier_potential_fit的包装器。警告
此函数需要CVXPY库
警告
接受任何后端,但会首先转换为Numpy,然后再转换回后端。
- Parameters:
Xs (类似数组 (n, d)) – 用于计算最佳值 phi 和 G 的源点
ys (数组-like (n,), 可选) – 参考点的类别,默认为单一类别
Xt (类数组 (n, d)) – 在参考点 X 处的梯度值
yt (可选) – 被忽略。
- Returns:
self – 返回自我。
- Return type:
参考文献
[58] François-Pierre Paty, Alexandre d’Aspremont, and Marco Cuturi. 正则性作为正则化: 在最优运输中的光滑和强凸Brenier势。发表于国际人工智能与统计会议,页码 1222–1232。PMLR,2020。
另请参见
ot.mapping.nearest_brenier_potential_fit在源数据和目标数据上拟合SSNB
- transform(Xs, ys=None)[源]
计算经过拟合的平滑强凸最近布雷涅尔势(SSNB)[58]的类别
ys的新源样本Xs的影像。输出为两个SSNB最优映射的影像,称为“下”势和“上”势(来自[59],定理3.14)。用于
nearest_brenier_potential_predict_bounds的包装器。警告
此函数需要CVXPY库
警告
接受任何后端,但会首先转换为Numpy,然后再转换回后端。
- Parameters:
Xs (类数组 (m, d)) – 输入源点
ys (: array_like (m,), optional) – 输入源点的类别,默认为单个类别
- Returns:
G_lu – Y处的上下界潜力的梯度(源输入的图像)
- Return type:
类似数组 (2, m, d)
参考文献
[58] François-Pierre Paty, Alexandre d’Aspremont, and Marco Cuturi. 正则性作为正则化: 在最优运输中的光滑和强凸Brenier势。发表于国际人工智能与统计会议,页码 1222–1232。PMLR,2020。
[59] Adrien B Taylor. 凸插值和一阶方法在凸优化中的性能估计。博士论文,洛万大学,洛万-拉-诺夫,比利时,2017年。
另请参见
ot.mapping.nearest_brenier_potential_predict_bounds在新源数据上预测SSNB图像
- class ot.da.SinkhornL1l2Transport(reg_e=1.0, reg_cl=0.1, max_iter=10, max_inner_iter=200, tol=1e-08, verbose=False, log=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=10)[源]
基于Sinkhorn算法的领域适应OT方法 + L1L2类正则化。
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
reg_cl (浮点型, 可选的 (默认值=0.1)) – 类的正则化参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (bool, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=10)) – 控制半监督模式。不同类别的标记源样本与目标样本之间的传输将表现出无限成本 (是成本矩阵最大值的10倍)
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “用于领域适应的最优传输,”发表于IEEE 模式分析与机器智能学报, 第PP卷,第99期,页码1-1
[2] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
使用 ot.da.SinkhornL1l2Transport 的示例
- class ot.da.SinkhornLpl1Transport(reg_e=1.0, reg_cl=0.1, max_iter=10, max_inner_iter=200, log=False, tol=1e-08, verbose=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=inf)[源]
基于Sinkhorn算法的领域适应OT方法 + LpL1类正则化。
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
reg_cl (浮点型, 可选的 (默认值=0.1)) – 类的正则化参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
log (bool, 可选 (默认=False)) – 控制优化算法的日志
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=np.inf)) – 控制半监督模式。不同类别的标记源样本和目标样本之间的传输将表现出由 limit_max 定义的成本。
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “用于领域适应的最优传输,”发表于IEEE 模式分析与机器智能学报, 第PP卷,第99期,页码1-1
[2] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
使用 ot.da.SinkhornLpl1Transport
- class ot.da.SinkhornTransport(reg_e=1.0, method='sinkhorn_log', max_iter=1000, tol=1e-08, verbose=False, log=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='continuous', limit_max=inf)[源]
基于Sinkhorn算法的领域自适应OT方法
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
max_iter (int, float, 可选 (默认=1000)) – 如果优化算法尚未收敛,则停止优化之前的最小迭代次数
tol (float, 可选 (默认=10e-9)) – 停止优化算法所需的精度。
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (int, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,规范化基准度量以避免在大度量值时发生的数值错误。接受的值为 ‘median’, ‘max’, ‘log’ 和 ‘loglog’。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (string, optional (default="continuous")) – 将一个领域的交通样本应用于另一个领域的样本映射的类型。目前唯一的可能选项是“ferradans”,它使用在[6]中提出的最近邻方法,而“continuous”使用[66]和[19]中的超样本方法。
limit_max (float, 可选 (默认=np.inf)) – 控制半监督模式。不同类别的标记源和目标样本之间的传输将表现出由此变量定义的成本
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[2] M. Cuturi, Sinkhorn 距离 : 快速计算最优传输,神经信息处理系统进展 (NIPS) 26, 2013
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
[19] Seguy, V., Bhushan Damodaran, B., Flamary, R., Courty, N., Rolet, A. & Blondel, M. 大规模最优传输和映射估计. 国际学习表示会议 (2018)
[66] Pooladian, Aram-Alexandre, 和 Jonathan Niles-Weed. “最佳运输映射的熵估计。” arXiv 预印本 arXiv:2109.12004 (2021).
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- inverse_transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将目标样本 \(\mathbf{X_t}\) 转移到源样本 \(\mathbf{X_s}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (数组类型, 形状 (n_target_samples,)) –
目标的类标签。如果某些目标样本没有标签,将 \(\mathbf{y_t}\)的元素填充为 -1。
警告:请注意,由于这个约定,-1不能用作类标签。
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xt – 运输目标样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (数组类型, 形状 (n_target_samples,)) –
目标的类标签。如果某些目标样本没有标签,将 \(\mathbf{y_t}\)的元素填充为 -1。
警告:请注意,由于这个约定,-1不能用作类标签。
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xs – 运输源样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
使用 ot.da.SinkhornTransport
- class ot.da.UnbalancedSinkhornTransport(reg_e=1.0, reg_m=0.1, method='sinkhorn', max_iter=10, tol=1e-09, verbose=False, log=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=10)[源]
基于Sinkhorn算法的领域适应不平衡优化传输方法
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
reg_m (float, 可选 (默认=0.1)) – 质量正则化参数
方法 (str) – 求解器使用的方法,可以是‘sinkhorn’,‘sinkhorn_stabilized’或‘sinkhorn_epsilon_scaling’,请参见这些函数以获取具体参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (bool, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=10)) – 控制半监督模式。不同类别的标记源样本与目标样本之间的传输将表现出无限成本 (是成本矩阵最大值的10倍)
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] Chizat, L., Peyré, G., Schmitzer, B., & Vialard, F. X. (2016). 用于不平衡运输问题的扩展算法。arXiv预印本 arXiv:1607.05816。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- class ot.da.BaseTransport[源]
OTDA对象的基类
注意
所有估计器应在其
__init__中将所有可以在类级别设置的参数指定为显式关键字参数(不使用*args或**kwargs)。fit 方法应该:
估计一个成本矩阵并将其存储在cost_属性中
估计耦合矩阵并将其存储在coupling_属性中
从源数据和目标数据估计分布,并将它们存储在 mu_s 和 mu_t 属性中
将 Xs 和 Xt 存储在属性中,以便在 transform 和 inverse_transform 方法中稍后使用
transform 方法应该始终接收一个 Xs 参数作为输入
inverse_transform 方法应该始终接收一个 Xt 参数作为输入
transform_labels 方法应该始终接收一个 ys 参数作为输入
inverse_transform_labels 方法应该始终接收一个 yt 参数作为输入
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 训练类标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- fit_transform(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建一个耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\) 并将源样本 \(\mathbf{X_s}\) 转换到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 训练样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
transp_Xs – 源样本样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- inverse_transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将目标样本 \(\mathbf{X_t}\) 转移到源样本 \(\mathbf{X_s}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (类数组, 形状 (n_target_samples,)) –
目标类标签。如果某些目标样本未标记,则用 -1 填充 \(\mathbf{y_t}\) 的元素。
警告:请注意,由于这种约定,-1 不能被用作 类标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xt – 被传输的目标样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- inverse_transform_labels(yt=None)[源]
传播目标标签 \(\mathbf{y_t}\) 以获取估计的源标签 \(\mathbf{y_s}\)
- Parameters:
yt (类数组, 形状 (n_target_samples,))
- Returns:
transp_ys – 估算的软源标签。
- Return type:
类数组,形状 (n_source_samples, nb_classes)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (数组类型, 形状 (n_target_samples,)) –
目标的类标签。如果某些目标样本没有标签,将 \(\mathbf{y_t}\)的元素填充为 -1。
警告:请注意,由于这个约定,-1不能用作类标签。
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xs – 运输源样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- transform_labels(ys=None)[源]
传播源标签 \(\mathbf{y_s}\) 以获得估计的目标标签,如在 [27] 中所示。
- Parameters:
ys (类似数组, 形状 (n_source_samples,)) – 源类标签
- Returns:
transp_ys – 估计的软目标标签。
- Return type:
类似数组,形状 (n_target_samples, nb_classes)
参考文献
[27] Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia “在目标偏移下的多源领域适应的最优传输”, 国际人工智能与统计会议 (AISTATS), 2019.
- class ot.da.EMDLaplaceTransport(reg_type='pos', reg_lap=1.0, reg_src=1.0, metric='sqeuclidean', norm=None, similarity='knn', similarity_param=None, max_iter=100, tol=1e-09, max_inner_iter=100000, inner_tol=1e-09, log=False, verbose=False, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans')[源]
基于地球移动者距离的领域适应OT方法,带拉普拉斯正则化
- Parameters:
reg_type (字符串 可选 (默认='pos')) – 正则化项的类型:‘pos’和‘disp’分别对应于在 [2] 和 [6] 中定义的正则化项。
reg_lap (float, 可选 (默认=1)) – 拉普拉斯正则化参数
reg_src (float, 可选 (默认=0.5)) – 正规化中的源相对重要性
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
相似度 (字符串, 可选的 (默认="knn")) – 使用的相似度,可以是knn或高斯
similarity_param (int 或 float, 可选 (默认=None)) – 相似度参数:最近邻的数量或带宽 如果相似度为“knn”或“gaussian”,分别。如果提供了None, 则分别设置为3或平均成对平方欧几里得距离。
max_iter (int, 可选 (默认=100)) – BCD迭代的最大次数
tol (float, 可选 (默认=1e-5)) – 相对损失减少的停止阈值 (>0)
max_inner_iter (int, 可选 (默认=10)) – 最大迭代次数(内部CG求解器)
inner_tol (float, 可选 (默认=1e-6)) – 停止阈值在误差上 (内层CG求解器) (>0)
log (int, 可选 (默认=False)) – 控制优化算法的日志
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[2] R. Flamary, N. Courty, D. Tuia, A. Rakotomamonjy, “带有拉普拉斯正则化的最优传输:应用于领域适应和形状匹配,” 在NIPS关于最优传输和机器学习OTML的研讨会,2014。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化离散最优传输. SIAM 图像科学期刊, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- class ot.da.EMDTransport(metric='sqeuclidean', norm=None, log=False, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=10, max_iter=100000)[源]
基于地球移动者距离的领域适应OT方法
- Parameters:
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
log (int, 可选 (默认=False)) – 控制优化算法的日志
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=10)) – 控制半监督模式。不同类别的标记源样本与目标样本之间的传输将表现出无限成本 (是成本矩阵最大值的10倍)
max_iter (int, 可选 (默认=100000)) – 在优化算法尚未收敛时,停止优化前的最大迭代次数。
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- class ot.da.JCPOTTransport(reg_e=0.1, max_iter=10, tol=1e-08, verbose=False, log=False, metric='sqeuclidean', out_of_sample_map='ferradans')[源]
基于Wasserstein重心算法的多源目标偏移域适应OT方法。
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (bool, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
- coupling_
每个源域与目标域之间的最优配对集
- Type:
形状为 K x (n_source_samples, n_target_samples) 的类数组对象列表
- proportions_
目标领域中的估计类别比例
- Type:
类数组,形状为 (n_classes,)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia “针对目标偏移的多源领域适应的最优传输”, 国际人工智能与统计会议(AISTATS), 第89卷,页849-858,2019年。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本和目标样本集的列表构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
- Returns:
self – 返回自我。
- Return type:
- inverse_transform_labels(yt=None)[源]
传播目标标签 \(\mathbf{y_t}\) 以获取估计的源标签 \(\mathbf{y_s}\)
- Parameters:
yt (数组类似, 形状 (n_target_samples,)) – 目标类别标签
- Returns:
transp_ys – 估计的软源标签列表
- Return type:
K个类数组对象的列表,形状为 K x (nk_source_samples, nb_classes)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (列表 包含 K 个类似数组的对象, 形状为 K x (nk_source_samples, n_features)) – 训练输入样本的列表。
ys (列表 of K 类似数组的对象, 形状 K x (nk_source_samples,)) – 标签的列表
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- transform_labels(ys=None)[源]
传播源标签 \(\mathbf{y_s}\) 以获得目标标签,如在 [27]
- Parameters:
ys (list 的 K 类数组对象, 形状 K x (nk_source_samples,)) – 类别标签的列表
- Returns:
yt – 估计的软目标标签。
- Return type:
类似数组,形状 (n_target_samples, nb_classes)
参考文献
[27] Ievgen Redko, Nicolas Courty, Rémi Flamary, Devis Tuia “在目标偏移下的多源领域适应的最优传输”, 国际人工智能与统计会议 (AISTATS), 2019.
- class ot.da.LinearGWTransport(log=False, sign_eigs=None, distribution_estimation=<function distribution_estimation_uniform>)[源]
经验分布之间的OT高斯Gromov-Wasserstein线性算子
该函数估计最佳线性算子,以便在Gromov-Wasserstein距离上最佳地对齐两个经验分布。这相当于估计两个高斯分布之间的闭式映射 \(\mathcal{N}(\mu_s,\Sigma_s)\) 和 \(\mathcal{N}(\mu_t,\Sigma_t)\),正如在[57]中提出的。
从源到目标的线性算子 \(M\)
\[M(\mathbf{x})= \mathbf{A} \mathbf{x} + \mathbf{b}\]其中矩阵 \(\mathbf{A}\) 和向量 \(\mathbf{b}\) 在 [57] 中定义。
- Parameters:
参考文献
[57] Delon, J., Desolneux, A., & Salmona, A. (2022). Gromov–Wasserstein 高斯分布之间的距离。应用概率杂志, 59(4), 1178-1198。
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- class ot.da.LinearTransport(reg=1e-08, bias=True, log=False, distribution_estimation=<function distribution_estimation_uniform>)[源]
经验分布之间的OT线性算子
该函数估计了最佳线性算子,以对齐两个经验分布。这相当于估计两个高斯分布之间的闭合形式映射 \(\mathcal{N}(\mu_s,\Sigma_s)\) 和 \(\mathcal{N}(\mu_t,\Sigma_t)\),如在 [14] 中提出,并在 [15] 的备注2.29中讨论。
从源到目标的线性算子 \(M\)
\[M(\mathbf{x})= \mathbf{A} \mathbf{x} + \mathbf{b}\]其中 :
\[ \begin{align}\begin{aligned}\mathbf{A} &= \Sigma_s^{-1/2} \left(\Sigma_s^{1/2}\Sigma_t\Sigma_s^{1/2} \right)^{1/2} \Sigma_s^{-1/2}\\\mathbf{b} &= \mu_t - \mathbf{A} \mu_s\end{aligned}\end{align} \]- Parameters:
参考文献
[14] Knott, M. 和 Smith, C. S. “关于分布的最优映射”,优化理论与应用期刊 第43卷,1984年
[15] Peyré, G., & Cuturi, M. (2017). “计算最优运输”, 2018.
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- inverse_transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将目标样本 \(\mathbf{X_t}\) 转移到源样本 \(\mathbf{X_s}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xt – 被传输的目标样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xs – 运输源样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- class ot.da.MappingTransport(mu=1, eta=0.001, bias=False, metric='sqeuclidean', norm=None, kernel='linear', sigma=1, max_iter=100, tol=1e-05, max_inner_iter=10, inner_tol=1e-06, log=False, verbose=False, verbose2=False)[源]
MappingTransport:旨在联合估计最优传输耦合及相关映射的DA方法
- Parameters:
mu (float, 可选 (默认=1)) – 线性OT损失的权重 (>0)
eta (float, 可选 (默认=0.001)) – 线性映射 L 的正则化项 (>0)
偏差 (布尔值, 可选的 (默认=False)) – 估计具有恒定偏差的线性映射
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
核函数 (字符串, 可选 (默认="线性")) – 使用的核函数可以是线性或高斯
sigma (float, 可选 (默认=1)) – 高斯核参数
max_iter (int, 可选 (默认=100)) – BCD迭代的最大次数
tol (float, 可选 (默认=1e-5)) – 相对损失减少的停止阈值 (>0)
max_inner_iter (int, 可选 (默认=10)) – 最大迭代次数(内部CG求解器)
inner_tol (float, 可选 (默认=1e-6)) – 停止阈值在误差上 (内层CG求解器) (>0)
log (bool, 可选 (默认为False)) – 如果为True,则记录日志
verbose (bool, 可选 (默认=False)) – 在迭代过程中打印信息
verbose2 (bool, 可选 (默认=False)) – 在迭代过程中打印信息
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- mapping_
相关映射
数组类型,形状 (n_features (+ 1), n_features), (如果有偏差)当核函数为线性时
类数组,形状 (n_source_samples (+ 1), n_features), (如果有偏置) 当核 == 高斯时
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[8] M. Perrot, N. Courty, R. Flamary, A. Habrard, “离散最优传输的映射估计”, 神经信息处理系统 (NIPS), 2016.
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
构建最佳耦合并估计来自源样本和目标样本集的相关映射 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自身
- Return type:
- class ot.da.NearestBrenierPotential(strongly_convex_constant=0.6, gradient_lipschitz_constant=1.4, log=False, its=100, seed=None)[源]
光滑强凸最近Brenier势 (SSNB) 是一种来自 [58] 的方法,它计算具有L-利普希茨梯度的l-强凸势 \(\varphi\),使得 \(\nabla \varphi \# \mu \approx \nu\)。这种规则性只能在环境空间的一个划分的分量上被强加(由点类编码),这相比于强制全局规则性是一种放松。
SSNBs通过解决优化问题来接近目标度量:
\begin{gather*} \varphi \in \text{argmin}_{\varphi \in \mathcal{F}}\ \text{W}_2(\nabla \varphi \#\mu_s, \mu_t), \end{gather*}其中 \(\mathcal{F}\) 是在每个集合 \(E_k\) l-强凸的空间函数,具有L-Lipschitz梯度,给定 \((E_k)_{k \in [K]}\) 是环境源空间的一个划分。
该问题通过“拟合”源数据和目标数据来解决,使用凸二次约束二次规划,得到值
phi和源点处的梯度G。然后,通过在每个点上解决(更简单的)二次约束线性规划,使用拟合“参数”phi和G来找到“新”源样本的图像。我们提供了两种可能的图像,分别对应于“下限”和“上限势”([59], 定理 3.14)。这两种图像都是SSNB问题的最优解,并可以在实践中使用。警告
此函数需要CVXPY库
警告
接受任何后端,但会首先转换为Numpy,然后再转换回后端。
- Parameters:
参考文献
[58] François-Pierre Paty, Alexandre d’Aspremont, and Marco Cuturi. 正则性作为正则化: 在最优运输中的光滑和强凸Brenier势。发表于国际人工智能与统计会议,页码 1222–1232。PMLR,2020。
[59] Adrien B Taylor. 凸插值和一阶方法在凸优化中的性能估计。博士论文,洛万大学,洛万-拉-诺夫,比利时,2017年。
另请参见
ot.mapping.nearest_brenier_potential_fit在源数据和目标数据上拟合SSNB
ot.mapping.nearest_brenier_potential_predict_bounds在新源数据上预测SSNB图像
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
将平滑强凸最近布雷尼尔势能[58]拟合到源数据
Xs到目标数据Xt,分区由(可选的)标签ys给出。用于
ot.mapping.nearest_brenier_potential_fit的包装器。警告
此函数需要CVXPY库
警告
接受任何后端,但会首先转换为Numpy,然后再转换回后端。
- Parameters:
Xs (类似数组 (n, d)) – 用于计算最佳值 phi 和 G 的源点
ys (数组-like (n,), 可选) – 参考点的类别,默认为单一类别
Xt (类数组 (n, d)) – 在参考点 X 处的梯度值
yt (可选) – 被忽略。
- Returns:
self – 返回自我。
- Return type:
参考文献
[58] François-Pierre Paty, Alexandre d’Aspremont, and Marco Cuturi. 正则性作为正则化: 在最优运输中的光滑和强凸Brenier势。发表于国际人工智能与统计会议,页码 1222–1232。PMLR,2020。
另请参见
ot.mapping.nearest_brenier_potential_fit在源数据和目标数据上拟合SSNB
- transform(Xs, ys=None)[源]
计算经过拟合的平滑强凸最近布雷涅尔势(SSNB)[58]的类别
ys的新源样本Xs的影像。输出为两个SSNB最优映射的影像,称为“下”势和“上”势(来自[59],定理3.14)。用于
nearest_brenier_potential_predict_bounds的包装器。警告
此函数需要CVXPY库
警告
接受任何后端,但会首先转换为Numpy,然后再转换回后端。
- Parameters:
Xs (类数组 (m, d)) – 输入源点
ys (: array_like (m,), optional) – 输入源点的类别,默认为单个类别
- Returns:
G_lu – Y处的上下界潜力的梯度(源输入的图像)
- Return type:
类似数组 (2, m, d)
参考文献
[58] François-Pierre Paty, Alexandre d’Aspremont, and Marco Cuturi. 正则性作为正则化: 在最优运输中的光滑和强凸Brenier势。发表于国际人工智能与统计会议,页码 1222–1232。PMLR,2020。
[59] Adrien B Taylor. 凸插值和一阶方法在凸优化中的性能估计。博士论文,洛万大学,洛万-拉-诺夫,比利时,2017年。
另请参见
ot.mapping.nearest_brenier_potential_predict_bounds在新源数据上预测SSNB图像
- class ot.da.SinkhornL1l2Transport(reg_e=1.0, reg_cl=0.1, max_iter=10, max_inner_iter=200, tol=1e-08, verbose=False, log=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=10)[源]
基于Sinkhorn算法的领域适应OT方法 + L1L2类正则化。
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
reg_cl (浮点型, 可选的 (默认值=0.1)) – 类的正则化参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (bool, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=10)) – 控制半监督模式。不同类别的标记源样本与目标样本之间的传输将表现出无限成本 (是成本矩阵最大值的10倍)
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “用于领域适应的最优传输,”发表于IEEE 模式分析与机器智能学报, 第PP卷,第99期,页码1-1
[2] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- class ot.da.SinkhornLpl1Transport(reg_e=1.0, reg_cl=0.1, max_iter=10, max_inner_iter=200, log=False, tol=1e-08, verbose=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=inf)[源]
基于Sinkhorn算法的领域适应OT方法 + LpL1类正则化。
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
reg_cl (浮点型, 可选的 (默认值=0.1)) – 类的正则化参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
log (bool, 可选 (默认=False)) – 控制优化算法的日志
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=np.inf)) – 控制半监督模式。不同类别的标记源样本和目标样本之间的传输将表现出由 limit_max 定义的成本。
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “用于领域适应的最优传输,”发表于IEEE 模式分析与机器智能学报, 第PP卷,第99期,页码1-1
[2] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- class ot.da.SinkhornTransport(reg_e=1.0, method='sinkhorn_log', max_iter=1000, tol=1e-08, verbose=False, log=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='continuous', limit_max=inf)[源]
基于Sinkhorn算法的领域自适应OT方法
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
max_iter (int, float, 可选 (默认=1000)) – 如果优化算法尚未收敛,则停止优化之前的最小迭代次数
tol (float, 可选 (默认=10e-9)) – 停止优化算法所需的精度。
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (int, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,规范化基准度量以避免在大度量值时发生的数值错误。接受的值为 ‘median’, ‘max’, ‘log’ 和 ‘loglog’。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (string, optional (default="continuous")) – 将一个领域的交通样本应用于另一个领域的样本映射的类型。目前唯一的可能选项是“ferradans”,它使用在[6]中提出的最近邻方法,而“continuous”使用[66]和[19]中的超样本方法。
limit_max (float, 可选 (默认=np.inf)) – 控制半监督模式。不同类别的标记源和目标样本之间的传输将表现出由此变量定义的成本
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[2] M. Cuturi, Sinkhorn 距离 : 快速计算最优传输,神经信息处理系统进展 (NIPS) 26, 2013
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
[19] Seguy, V., Bhushan Damodaran, B., Flamary, R., Courty, N., Rolet, A. & Blondel, M. 大规模最优传输和映射估计. 国际学习表示会议 (2018)
[66] Pooladian, Aram-Alexandre, 和 Jonathan Niles-Weed. “最佳运输映射的熵估计。” arXiv 预印本 arXiv:2109.12004 (2021).
- fit(Xs=None, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- inverse_transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将目标样本 \(\mathbf{X_t}\) 转移到源样本 \(\mathbf{X_s}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (数组类型, 形状 (n_target_samples,)) –
目标的类标签。如果某些目标样本没有标签,将 \(\mathbf{y_t}\)的元素填充为 -1。
警告:请注意,由于这个约定,-1不能用作类标签。
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xt – 运输目标样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- transform(Xs=None, ys=None, Xt=None, yt=None, batch_size=128)[源]
将源样本 \(\mathbf{X_s}\) 转移到目标样本 \(\mathbf{X_t}\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 源输入样本。
ys (类数组, 形状 (n_source_samples,)) – 源样本的类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 目标输入样本。
yt (数组类型, 形状 (n_target_samples,)) –
目标的类标签。如果某些目标样本没有标签,将 \(\mathbf{y_t}\)的元素填充为 -1。
警告:请注意,由于这个约定,-1不能用作类标签。
batch_size (int, 可选 (默认=128)) – 用于样本外逆变换的批量大小
- Returns:
transp_Xs – 运输源样本。
- Return type:
类数组,形状 (n_source_samples, n_features)
- class ot.da.UnbalancedSinkhornTransport(reg_e=1.0, reg_m=0.1, method='sinkhorn', max_iter=10, tol=1e-09, verbose=False, log=False, metric='sqeuclidean', norm=None, distribution_estimation=<function distribution_estimation_uniform>, out_of_sample_map='ferradans', limit_max=10)[源]
基于Sinkhorn算法的领域适应不平衡优化传输方法
- Parameters:
reg_e (float, 可选 (默认=1)) – 熵正则化参数
reg_m (float, 可选 (默认=0.1)) – 质量正则化参数
方法 (str) – 求解器使用的方法,可以是‘sinkhorn’,‘sinkhorn_stabilized’或‘sinkhorn_epsilon_scaling’,请参见这些函数以获取具体参数
max_iter (int, float, 可选 (默认=10)) – 如果优化算法尚未收敛,则停止优化前的最小迭代次数
tol (浮点数, 可选 (默认=10e-9)) – 错误的停止阈值(内部sinkhorn求解器) (>0)
verbose (bool, 可选 (默认=False)) – 控制优化算法的详细程度
log (bool, 可选 (默认=False)) – 控制优化算法的日志
metric (string, 可选 (默认="sqeuclidean")) – Wasserstein 问题的基础度量
norm (string, optional (default=None)) – 如果给定,归一化地面度量以避免在大度量值时可能发生的数值误差。
distribution_estimation (callable, 可选 (默认为均匀分布)) – 要使用的分布估计的类型
out_of_sample_map (字符串, 可选的 (默认="ferradans")) – 要应用于将运输样本从一个领域映射到另一个领域的样本映射类型。目前唯一可能的选项是“ferradans”,它使用了[6]中提出的方法。
limit_max (float, 可选 (默认=10)) – 控制半监督模式。不同类别的标记源样本与目标样本之间的传输将表现出无限成本 (是成本矩阵最大值的10倍)
- coupling_
最佳耦合
- Type:
类数组,形状 (n_source_samples, n_target_samples)
- log_
日志的字典,如果参数 log 不为 True,则为空字典
- Type:
字典
参考文献
[1] Chizat, L., Peyré, G., Schmitzer, B., & Vialard, F. X. (2016). 用于不平衡运输问题的扩展算法。arXiv预印本 arXiv:1607.05816。
[6] Ferradans, S., Papadakis, N., Peyré, G., & Aujol, J. F. (2014). 正则化的离散最优传输。SIAM 成像科学杂志, 7(3), 1853-1882.
- fit(Xs, ys=None, Xt=None, yt=None)[源]
从源样本集和目标样本集构建耦合矩阵 \((\mathbf{X_s}, \mathbf{y_s})\) 和 \((\mathbf{X_t}, \mathbf{y_t})\)
- Parameters:
Xs (类数组, 形状 (n_source_samples, n_features)) – 训练输入样本。
ys (类数组, 形状 (n_source_samples,)) – 类别标签
Xt (类似数组, 形状 (n_target_samples, n_features)) – 训练输入样本。
yt (类似数组, 形状 (n_target_samples,)) –
类别标签。如果某些目标样本没有标签,则用 \(\mathbf{y_t}\) 的元素填充 -1。
警告:请注意,由于该约定,-1 不能作为类别标签
- Returns:
self – 返回自我。
- Return type:
- ot.da.distribution_estimation_uniform(X)[源]
从样本数组中估算一个均匀分布 \(\mathbf{X}\)
- Parameters:
X (类似数组, 形状 (样本数量, 特征数量)) – 样本数组
- Returns:
mu – 从 \(\mathbf{X}\) 估计的均匀分布
- Return type:
类似数组,形状为 (n_samples,)
- ot.da.emd_laplace(a, b, xs, xt, M, sim='knn', sim_param=None, reg='pos', eta=1, alpha=0.5, numItermax=100, stopThr=1e-09, numInnerItermax=100000, stopInnerThr=1e-09, log=False, verbose=False)[源]
解决带有拉普拉斯正则化的最优传输问题(OT)
\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \eta \cdot \Omega_\alpha(\gamma)\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]其中:
\(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重(总和为1)
\(\mathbf{x_s}\) 和 \(\mathbf{x_t}\) 是源样本和目标样本
\(\mathbf{M}\) 是 (ns, nt) 计量成本矩阵
\(\Omega_\alpha\) 是拉普拉斯正则化项
\[\Omega_\alpha = \frac{1 - \alpha}{n_s^2} \sum_{i,j} \mathbf{S^s}_{i,j} \|T(\mathbf{x}^s_i) - T(\mathbf{x}^s_j) \|^2 + \frac{\alpha}{n_t^2} \sum_{i,j} \mathbf{S^t}_{i,j} \|T(\mathbf{x}^t_i) - T(\mathbf{x}^t_j) \|^2\]其中 \(\mathbf{S^s}_{i,j}, \mathbf{S^t}_{i,j}\) 表示源和目标相似性矩阵,\(T(\cdot)\) 是一个重心映射。
用于解决该问题的算法是条件梯度算法,如[5]中提出的。
- Parameters:
a (类数组 (ns,)) – 源域中的样本权重
b (类数组 (nt,)) – 目标领域中的样本权重
xs (类似数组 (ns,d)) – 源领域中的样本
xt (类数组 (nt,d)) – 目标领域中的样本
M (数组-like (ns,nt)) – 损失矩阵
sim (string, optional) – 相似度的类型(‘knn’ 或 ‘gauss’),用于构建拉普拉斯算子。
sim_param (int 或 float, 可选) – 参数(用于计算拉普拉斯算子时,sim=’knn’的最近邻数量或sim=’gauss’的带宽)。
reg (string) – 拉普拉斯正则化的类型
eta (float) – 拉普拉斯正则化的正则化项
alpha (float) – 源域在正则化中的重要性正则化项
numItermax (int, 可选) – 最大迭代次数
stopThr (float, 可选) – 错误停止阈值(内部 emd 求解器)(>0)
numInnerItermax (int, 可选) – 最大迭代次数(内层CG求解器)
stopInnerThr (float, 可选) – 错误的停止阈值(内部CG求解器) (>0)
verbose (bool, 可选) – 在迭代过程中打印信息
log (bool, 可选) – 如果为真,则记录日志
- Returns:
gamma ((ns, nt) 类数组) – 给定参数的最优运输矩阵
log (字典) – 仅当参数中的 log==True 时返回日志字典
参考文献
[5] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优传输用于领域适应,”发表在IEEE 模式分析与机器智能学报, 第PP卷,第99期,第1-1页
[30] R. Flamary, N. Courty, D. Tuia, A. Rakotomamonjy, “带有拉普拉斯正则化的最优传输:应用于领域适应和形状匹配,” 在NIPS关于最优传输和机器学习OTML的研讨会,2014。
另请参见
ot.lp.emd未正则化的OT
ot.optim.cg通用正则化OT
- ot.da.sinkhorn_l1l2_gl(a, labels_a, b, M, reg, eta=0.1, numItermax=10, numInnerItermax=200, stopInnerThr=1e-09, eps=1e-12, verbose=False, log=False)[源]
解决带有群体套索正则化的熵正则化最优传输问题
该函数解决以下优化问题:
\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \mathrm{reg} \cdot \Omega_e(\gamma) + \eta \ \Omega_g(\gamma)\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]其中 :
\(\mathbf{M}\) 是 (ns, nt) 计量成本矩阵
\(\Omega_e\) 是熵正则化项 \(\Omega_e(\gamma)=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)
\(\Omega_g\) 是组套索正则化项 \(\Omega_g(\gamma)=\sum_{i,c} \|\gamma_{i,\mathcal{I}_c}\|^2\) 其中 \(\mathcal{I}_c\) 是源域中类别c的样本索引。
\(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重(总和为1)
用于解决该问题的算法是广义条件梯度,如[5, 7]中所提出的。
- Parameters:
a (类数组 (ns,)) – 源域中的样本权重
labels_a (类似数组 (ns,)) – 源域中样本的标签
b (类数组 (nt,)) – 目标域中的样本
M (数组-like (ns,nt)) – 损失矩阵
reg (float) – 熵正则化的正则化项 >0
eta (float, 可选) – 组套索正则化的正则化项 >0
numItermax (int, 可选) – 最大迭代次数
numInnerItermax (int, 可选) – 最大迭代次数(内部Sinkhorn求解器)
stopInnerThr (float, 可选) – 错误的停止阈值(内部Sinkhorn求解器) (>0)
eps (float, 可选 (默认=1e-12)) – 避免除以零的小值
verbose (bool, 可选) – 在迭代过程中打印信息
log (bool, 可选) – 如果为真,则记录日志
- Returns:
gamma ((ns, nt) 类数组) – 给定参数的最优运输矩阵
log (字典) – 仅当参数中的 log==True 时返回日志字典
参考文献
[5] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “最优运输用于领域适应,” 见于 IEEE Transactions on Pattern Analysis and Machine Intelligence , vol.PP, no.99, pp.1-1
[7] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
另请参见
ot.optim.gcgOT 问题的一般条件梯度
- ot.da.sinkhorn_lpl1_mm(a, labels_a, b, M, reg, eta=0.1, numItermax=10, numInnerItermax=200, stopInnerThr=1e-09, verbose=False, log=False)[源]
解决具有非凸组lasso正则化的熵正则化最优传输问题
该函数解决以下优化问题:
\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \mathrm{reg} \cdot \Omega_e(\gamma) + \eta \ \Omega_g(\gamma)\\s.t. \ \gamma \mathbf{1} = \mathbf{a}\\ \gamma^T \mathbf{1} = \mathbf{b}\\ \gamma \geq 0\end{aligned}\end{align} \]其中 :
\(\mathbf{M}\) 是 (ns, nt) 计量成本矩阵
\(\Omega_e\) 是熵正则化项 \(\Omega_e (\gamma)=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)
\(\Omega_g\) 是组lasso正则化项 \(\Omega_g(\gamma)=\sum_{i,c} \|\gamma_{i,\mathcal{I}_c}\|^{1/2}_1\) 其中 \(\mathcal{I}_c\) 是源域中来自类 c 的样本索引。
\(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重(总和为1)
用于解决问题的算法是广义条件梯度,如[5, 7]中提出的。
- Parameters:
a (类数组 (ns,)) – 源域中的样本权重
labels_a (类似数组 (ns,)) – 源域中样本的标签
b (类数组 (nt,)) – 目标领域中的样本权重
M (数组-like (ns,nt)) – 损失矩阵
reg (float) – 熵正则化的正则化项 >0
eta (float, 可选) – 组套索正则化的正则化项 >0
numItermax (int, 可选) – 最大迭代次数
numInnerItermax (int, 可选) – 最大迭代次数(内部Sinkhorn求解器)
stopInnerThr (float, 可选) – 错误的停止阈值(内部Sinkhorn求解器) (>0)
verbose (bool, 可选) – 在迭代过程中打印信息
log (bool, 可选) – 如果为真,则记录日志
- Returns:
gamma ((ns, nt) 类数组) – 给定参数的最优运输矩阵
log (字典) – 仅当参数中的 log==True 时返回日志字典
参考文献
[5] N. Courty; R. Flamary; D. Tuia; A. Rakotomamonjy, “用于领域适应的最优传输,”发表于IEEE 模式分析与机器智能学报, 第PP卷,第99期,页码1-1
[7] Rakotomamonjy, A., Flamary, R., & Courty, N. (2015). 广义条件梯度:收敛分析及应用。arXiv 预印本 arXiv:1510.06567。
另请参见
ot.lp.emd未正则化的OT
ot.bregman.sinkhorn熵正则化最优传输
ot.optim.cg通用正则化OT