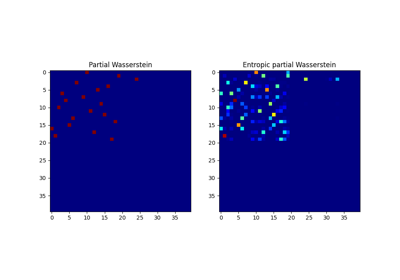
ot.partial

部分OT求解器

函数

ot.partial.entropic_partial_gromov_wasserstein(C1, C2, p, q, reg, m=None, G0=None, numItermax=1000, tol=1e-07, log=False, verbose=False)

返回部分Gromov-Wasserstein传输在 \((\mathbf{C_1}, \mathbf{p})\) 和 \((\mathbf{C_2}, \mathbf{q})\)之间

该函数解决以下优化问题：

\[\gamma = \mathop{\arg \min}_{\gamma} \quad \sum_{i,j,k,l} L(\mathbf{C_1}_{i,k}, \mathbf{C_2}_{j,l})\cdot \gamma_{i,j}\cdot\gamma_{k,l} + \mathrm{reg} \cdot\Omega(\gamma)\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma &\geq 0\\ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{C_1}\) 是源空间中的度量成本矩阵

• \(\mathbf{C_2}\) 是目标空间中的度量成本矩阵

• \(\mathbf{p}\) 和 \(\mathbf{q}\) 是样本权重

• L: 二次损失函数

• \(\Omega\) 是熵正则化项， \(\Omega=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• m 是要运输的质量量

GW问题的表述已在 [12]中提出，部分GW则在[29]中提出

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.entropic_partial_gromov_wasserstein 替代。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• reg (float) – 熵正则化参数

• m (float, 可选) – 要运输的质量量 (默认: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\))

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止阈值在误差上 (>0)

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(entropic_partial_gromov_wasserstein(C1, C2, a, b, 50), 2)
array([[0.12, 0.13, 0.  , 0.  ],
       [0.13, 0.12, 0.  , 0.  ],
       [0.  , 0.  , 0.25, 0.  ],
       [0.  , 0.  , 0.  , 0.25]])
>>> np.round(entropic_partial_gromov_wasserstein(C1, C2, a, b, 50,0.25), 2)
array([[0.02, 0.03, 0.  , 0.03],
       [0.03, 0.03, 0.  , 0.03],
       [0.  , 0.  , 0.03, 0.  ],
       [0.02, 0.02, 0.  , 0.03]])

Returns:

• 数学: gamma : (dim_a, dim_b) ndarray – 针对给定参数的最优运输矩阵

• log (dict) – 仅当 log 为 True 时返回日志字典

参考文献

[12]

Peyré, Gabriel, Marco Cuturi, 和 Justin Solomon, “Gromov-Wasserstein 平均化核与距离矩阵。” 国际机器学习会议 (ICML). 2016.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

另请参见

ot.partial.partial_gromov_wasserstein

精确的部分Gromov-Wasserstein

ot.partial.entropic_partial_gromov_wasserstein2(C1, C2, p, q, reg, m=None, G0=None, numItermax=1000, tol=1e-07, log=False, verbose=False)

返回\((\mathbf{C_1}, \mathbf{p})\)和\((\mathbf{C_2}, \mathbf{q})\)之间的部分Gromov-Wasserstein差异

该函数解决以下优化问题：

\[GW = \min_{\gamma} \quad \sum_{i,j,k,l} L(\mathbf{C_1}_{i,k}, \mathbf{C_2}_{j,l})\cdot \gamma_{i,j}\cdot\gamma_{k,l} + \mathrm{reg} \cdot\Omega(\gamma)\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma &\geq 0\\ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{C_1}\) 是源空间中的度量成本矩阵

• \(\mathbf{C_2}\) 是目标空间中的度量成本矩阵

• \(\mathbf{p}\) 和 \(\mathbf{q}\) 是样本权重

• L : 二次损失函数

• \(\Omega\) 是熵正则化项， \(\Omega=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• m 是要运输的质量量

GW问题的表述已在 [12]中提出，部分GW则在[29]中提出

注意

该函数将在不久的将来被弃用，请使用

请使用ot.gromov.entropic_partial_gromov_wasserstein2。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• reg (float) – 熵正则化参数

• m (float, 可选) – 要运输的质量量 (默认: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\))

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止阈值在误差上 (>0)

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

Returns:

• partial_gw_dist (float) – Gromov-Wasserstein 距离

• log (dict) – 仅当 log 为 True 时返回的日志字典

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(entropic_partial_gromov_wasserstein2(C1, C2, a, b,50), 2)
1.87

参考文献

[12]

Peyré, Gabriel, Marco Cuturi, 和 Justin Solomon, “Gromov-Wasserstein 平均化核与距离矩阵。” 国际机器学习会议 (ICML). 2016.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.entropic_partial_wasserstein(a, b, M, reg, m=None, numItermax=1000, stopThr=1e-100, verbose=False, log=False)

解决部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \mathrm{reg} \cdot\Omega(\gamma)\\\begin{split}s.t. \gamma \mathbf{1} &\leq \mathbf{a} \\ \gamma^T \mathbf{1} &\leq \mathbf{b} \\ \gamma &\geq 0 \\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\} \\\end{split}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\Omega\) 是熵正则化项， \(\Omega=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

• m 是要运输的质量量

该问题的表述已在 [3] (prop. 5) 中提出

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 成本矩阵

• reg (float) – 正则化项 > 0

• m (float, 可选) – 要运输的质量量

• numItermax (int, 可选) – 最大迭代次数

• stopThr (float, 可选) – 错误的停止阈值 (>0)

• verbose (bool, 可选) – 在迭代过程中打印信息

• log (bool, 可选) – 如果为真，则记录日志

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> a = [.1, .2]
>>> b = [.1, .1]
>>> M = [[0., 1.], [2., 3.]]
>>> np.round(entropic_partial_wasserstein(a, b, M, 1, 0.1), 2)
array([[0.06, 0.02],
       [0.01, 0.  ]])

参考文献

[3]

Benamou, J. D., Carlier, G., Cuturi, M., Nenna, L., & Peyré, G. (2015). 用于正则化运输问题的迭代Bregman投影。 SIAM科学计算杂志，37(2)，A1111-A1138。

另请参见

ot.partial.partial_wasserstein

精确部分瓦瑟斯坦

使用 ot.partial.entropic_partial_wasserstein 的示例

部分Wasserstein和Gromov-Wasserstein示例

部分沃瑟斯坦和格罗莫夫-沃瑟斯坦示例

ot.partial.gwgrad_partial(C1, C2, T)

计算GW梯度。注意：我们不能使用[12]中的技巧，因为边际可能无法总和为1。

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.gwggrad 代替。

Parameters:

• C1 (数组，形状（n_p，n_p）) – 源内（P）成本矩阵

• C2 (数组，形状 (n_u,n_u)) – 目标内部 (U) 成本矩阵

• T (数组，形状(n_p+nb_dummies, n_u) (默认: None)) – 运输矩阵

Returns:

梯度

Return type:

numpy.array 形状为 (n_p+nb_dummies, n_u)

参考文献

[12]

Peyré, Gabriel, Marco Cuturi, 和 Justin Solomon, “Gromov-Wasserstein 平均化核与距离矩阵。” 国际机器学习会议 (ICML). 2016.

ot.partial.gwloss_partial(C1, C2, T)

计算GW损失。

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.gwloss 替代。

Parameters:

• C1 (数组，形状（n_p，n_p）) – 源内（P）成本矩阵

• C2 (数组，形状 (n_u,n_u)) – 目标内部 (U) 成本矩阵

• T (数组，形状(n_p+nb_dummies, n_u) (默认: None)) – 运输矩阵

Return type:

GW损失

ot.partial.partial_gromov_wasserstein(C1, C2, p, q, m=None, nb_dummies=1, G0=None, thres=1, numItermax=1000, tol=1e-07, log=False, verbose=False, **kwargs)

解决部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\Omega\) 是熵正则化项， \(\Omega(\gamma) = \sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

• m 是要运输的质量量

该问题的公式已在 [29]中提出

注意

该函数将在不久的将来被弃用，请使用

请使用 ot.gromov.partial_gromov_wasserstein 代替。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• m (float, 可选) – 要运输的质量量（默认值: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\)）

• nb_dummies (int, 可选) – 要添加的虚拟点数（避免EMD求解器的不稳定性）

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• thres (float, 可选) – 当为0时，用于填充成本矩阵的梯度矩阵的分位数（默认值：1）

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止迭代的容忍度

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(partial_gromov_wasserstein(C1, C2, a, b),2)
array([[0.  , 0.25, 0.  , 0.  ],
       [0.25, 0.  , 0.  , 0.  ],
       [0.  , 0.  , 0.25, 0.  ],
       [0.  , 0.  , 0.  , 0.25]])
>>> np.round(partial_gromov_wasserstein(C1, C2, a, b, m=0.25),2)
array([[0.  , 0.  , 0.  , 0.  ],
       [0.  , 0.  , 0.  , 0.  ],
       [0.  , 0.  , 0.25, 0.  ],
       [0.  , 0.  , 0.  , 0.  ]])

参考文献

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.partial_gromov_wasserstein2(C1, C2, p, q, m=None, nb_dummies=1, G0=None, thres=1, numItermax=1000, tol=1e-07, log=False, verbose=False, **kwargs)

解决部分最优运输问题并返回部分Gromov-Wasserstein差异

该函数考虑以下问题：

\[GW = \min_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\Omega\) 是熵正则化项， \(\Omega(\gamma) = \sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

• m 是要运输的质量量

该问题的公式已在 [29]中提出

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.partial_gromov_wasserstein2 替代。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• m (float, 可选) – 要运输的质量量（默认值: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\)）

• nb_dummies (int, 可选) – 要添加的虚拟点数（避免EMD求解器的不稳定性）

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• thres (float, 可选) – 当为0时，用于填充成本矩阵的梯度矩阵的分位数（默认值：1）

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止迭代的容忍度

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• partial_gw_dist (float) – 部分GW差异

• log (dict) – 仅当 log 为 True 时返回的日志字典

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(partial_gromov_wasserstein2(C1, C2, a, b),2)
1.69
>>> np.round(partial_gromov_wasserstein2(C1, C2, a, b, m=0.25),2)
0.0

参考文献

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.partial_wasserstein(a, b, M, m=None, nb_dummies=1, log=False, **kwargs)

解决二次成本的部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源和目标不平衡分布

• m 是要运输的质量量

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 二次成本的成本矩阵

• m (float, 可选) – 要运输的质量量

• nb_dummies (int, 可选, 默认:1) – 要添加的储备点的数量（为了避免数值不稳定，如果出现错误，请增加其值）

• log (bool, 可选) – 如果为真，则记录日志

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> a = [.1, .2]
>>> b = [.1, .1]
>>> M = [[0., 1.], [2., 3.]]
>>> np.round(partial_wasserstein(a,b,M), 2)
array([[0.1, 0. ],
       [0. , 0.1]])
>>> np.round(partial_wasserstein(a,b,M,m=0.1), 2)
array([[0.1, 0. ],
       [0. , 0. ]])

参考文献

[28]

Caffarelli, L. A., & McCann, R. J. (2010) 最优运输和Monge-Ampere障碍问题中的自由边界。数学年鉴, 673-730.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

另请参见

ot.partial.partial_wasserstein_lagrange

部分瓦瑟斯坦（Wasserstein）与

正则化

ot.partial.entropic_partial_wasserstein

部分瓦瑟斯坦与 a

entropic

使用 ot.partial.partial_wasserstein 的示例

二维准确和熵不平衡最优传输的示例

精确和熵不平衡最优运输的二维示例

部分Wasserstein和Gromov-Wasserstein示例

部分沃瑟斯坦和格罗莫夫-沃瑟斯坦示例

ot.partial.partial_wasserstein2(a, b, M, m=None, nb_dummies=1, log=False, **kwargs)

解决二次成本的部分最优传输问题并返回部分GW差异

该函数考虑以下问题：

\[\gamma = \min_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源和目标不平衡分布

• m 是要运输的质量量

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 二次成本的成本矩阵

• m (float, 可选) – 要运输的质量量

• nb_dummies (int, 可选, 默认:1) – 要添加的储备点的数量（为了避免数值不稳定，如果出现错误，请增加其值）

• log (bool, 可选) – 如果为真，则记录日志

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• GW (float) – 部分GW差异

• log (dict) – 仅当 log 为 True 时返回日志字典

示例

>>> import ot
>>> a=[.1, .2]
>>> b=[.1, .1]
>>> M=[[0., 1.], [2., 3.]]
>>> np.round(partial_wasserstein2(a, b, M), 1)
0.3
>>> np.round(partial_wasserstein2(a,b,M,m=0.1), 1)
0.0

参考文献

[28]

Caffarelli, L. A., & McCann, R. J. (2010) 最优运输和Monge-Ampere障碍问题中的自由边界。数学年鉴, 673-730.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.partial_wasserstein_lagrange(a, b, M, reg_m=None, nb_dummies=1, log=False, **kwargs)

解决二次成本的部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, (\mathbf{M} - \lambda) \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m & \leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

或者等价地（见 Chizat, L., Peyré, G., Schmitzer, B., & Vialard, F. X. (2018). 一种在最优传输与费舍尔–拉奥度量之间的插值距离。计算数学基础, 18(1), 1-44。）

\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \sqrt{\frac{\lambda}{2} (\|\gamma \mathbf{1} - \mathbf{a}\|_1 + \|\gamma^T \mathbf{1} - \mathbf{b}\|_1)}\\\text{s.t.} \ \gamma \geq 0\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源和目标不平衡分布

• \(\lambda\) 是拉格朗日成本。调整其值可以实现要运输的给定质量 m

该问题的表述已在 [28]中提出

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 二次成本的成本矩阵

• reg_m (浮动, 可选) – 拉格朗日成本

• nb_dummies (int, 可选, 默认:1) – 要添加的储备点的数量（为了避免数值不稳定，如果出现错误，请增加其值）

• log (bool, 可选) – 如果为真，则记录日志

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> a = [.1, .2]
>>> b = [.1, .1]
>>> M = [[0., 1.], [2., 3.]]
>>> np.round(partial_wasserstein_lagrange(a,b,M), 2)
array([[0.1, 0. ],
       [0. , 0.1]])
>>> np.round(partial_wasserstein_lagrange(a,b,M,reg_m=2), 2)
array([[0.1, 0. ],
       [0. , 0. ]])

参考文献

[28]

Caffarelli, L. A., & McCann, R. J. (2010) 最优运输和Monge-Ampere障碍问题中的自由边界。数学年鉴, 673-730.

另请参见

ot.partial.partial_wasserstein

固定质量的部分瓦瑟斯坦距离

ot.partial.entropic_partial_gromov_wasserstein(C1, C2, p, q, reg, m=None, G0=None, numItermax=1000, tol=1e-07, log=False, verbose=False)

返回部分Gromov-Wasserstein传输在 \((\mathbf{C_1}, \mathbf{p})\) 和 \((\mathbf{C_2}, \mathbf{q})\)之间

该函数解决以下优化问题：

\[\gamma = \mathop{\arg \min}_{\gamma} \quad \sum_{i,j,k,l} L(\mathbf{C_1}_{i,k}, \mathbf{C_2}_{j,l})\cdot \gamma_{i,j}\cdot\gamma_{k,l} + \mathrm{reg} \cdot\Omega(\gamma)\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma &\geq 0\\ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{C_1}\) 是源空间中的度量成本矩阵

• \(\mathbf{C_2}\) 是目标空间中的度量成本矩阵

• \(\mathbf{p}\) 和 \(\mathbf{q}\) 是样本权重

• L: 二次损失函数

• \(\Omega\) 是熵正则化项， \(\Omega=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• m 是要运输的质量量

GW问题的表述已在 [12]中提出，部分GW则在[29]中提出

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.entropic_partial_gromov_wasserstein 替代。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• reg (float) – 熵正则化参数

• m (float, 可选) – 要运输的质量量 (默认: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\))

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止阈值在误差上 (>0)

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(entropic_partial_gromov_wasserstein(C1, C2, a, b, 50), 2)
array([[0.12, 0.13, 0.  , 0.  ],
       [0.13, 0.12, 0.  , 0.  ],
       [0.  , 0.  , 0.25, 0.  ],
       [0.  , 0.  , 0.  , 0.25]])
>>> np.round(entropic_partial_gromov_wasserstein(C1, C2, a, b, 50,0.25), 2)
array([[0.02, 0.03, 0.  , 0.03],
       [0.03, 0.03, 0.  , 0.03],
       [0.  , 0.  , 0.03, 0.  ],
       [0.02, 0.02, 0.  , 0.03]])

Returns:

• 数学: gamma : (dim_a, dim_b) ndarray – 针对给定参数的最优运输矩阵

• log (dict) – 仅当 log 为 True 时返回日志字典

参考文献

[12]

Peyré, Gabriel, Marco Cuturi, 和 Justin Solomon, “Gromov-Wasserstein 平均化核与距离矩阵。” 国际机器学习会议 (ICML). 2016.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

另请参见

ot.partial.partial_gromov_wasserstein

精确的部分Gromov-Wasserstein

ot.partial.entropic_partial_gromov_wasserstein2(C1, C2, p, q, reg, m=None, G0=None, numItermax=1000, tol=1e-07, log=False, verbose=False)

返回\((\mathbf{C_1}, \mathbf{p})\)和\((\mathbf{C_2}, \mathbf{q})\)之间的部分Gromov-Wasserstein差异

该函数解决以下优化问题：

\[GW = \min_{\gamma} \quad \sum_{i,j,k,l} L(\mathbf{C_1}_{i,k}, \mathbf{C_2}_{j,l})\cdot \gamma_{i,j}\cdot\gamma_{k,l} + \mathrm{reg} \cdot\Omega(\gamma)\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma &\geq 0\\ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{C_1}\) 是源空间中的度量成本矩阵

• \(\mathbf{C_2}\) 是目标空间中的度量成本矩阵

• \(\mathbf{p}\) 和 \(\mathbf{q}\) 是样本权重

• L : 二次损失函数

• \(\Omega\) 是熵正则化项， \(\Omega=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• m 是要运输的质量量

GW问题的表述已在 [12]中提出，部分GW则在[29]中提出

注意

该函数将在不久的将来被弃用，请使用

请使用ot.gromov.entropic_partial_gromov_wasserstein2。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• reg (float) – 熵正则化参数

• m (float, 可选) – 要运输的质量量 (默认: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\))

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止阈值在误差上 (>0)

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

Returns:

• partial_gw_dist (float) – Gromov-Wasserstein 距离

• log (dict) – 仅当 log 为 True 时返回的日志字典

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(entropic_partial_gromov_wasserstein2(C1, C2, a, b,50), 2)
1.87

参考文献

[12]

Peyré, Gabriel, Marco Cuturi, 和 Justin Solomon, “Gromov-Wasserstein 平均化核与距离矩阵。” 国际机器学习会议 (ICML). 2016.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.entropic_partial_wasserstein(a, b, M, reg, m=None, numItermax=1000, stopThr=1e-100, verbose=False, log=False)

解决部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \mathrm{reg} \cdot\Omega(\gamma)\\\begin{split}s.t. \gamma \mathbf{1} &\leq \mathbf{a} \\ \gamma^T \mathbf{1} &\leq \mathbf{b} \\ \gamma &\geq 0 \\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\} \\\end{split}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\Omega\) 是熵正则化项， \(\Omega=\sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

• m 是要运输的质量量

该问题的表述已在 [3] (prop. 5) 中提出

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 成本矩阵

• reg (float) – 正则化项 > 0

• m (float, 可选) – 要运输的质量量

• numItermax (int, 可选) – 最大迭代次数

• stopThr (float, 可选) – 错误的停止阈值 (>0)

• verbose (bool, 可选) – 在迭代过程中打印信息

• log (bool, 可选) – 如果为真，则记录日志

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> a = [.1, .2]
>>> b = [.1, .1]
>>> M = [[0., 1.], [2., 3.]]
>>> np.round(entropic_partial_wasserstein(a, b, M, 1, 0.1), 2)
array([[0.06, 0.02],
       [0.01, 0.  ]])

参考文献

[3]

Benamou, J. D., Carlier, G., Cuturi, M., Nenna, L., & Peyré, G. (2015). 用于正则化运输问题的迭代Bregman投影。 SIAM科学计算杂志，37(2)，A1111-A1138。

另请参见

ot.partial.partial_wasserstein

精确部分瓦瑟斯坦

ot.partial.gwgrad_partial(C1, C2, T)

计算GW梯度。注意：我们不能使用[12]中的技巧，因为边际可能无法总和为1。

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.gwggrad 代替。

Parameters:

• C1 (数组，形状（n_p，n_p）) – 源内（P）成本矩阵

• C2 (数组，形状 (n_u,n_u)) – 目标内部 (U) 成本矩阵

• T (数组，形状(n_p+nb_dummies, n_u) (默认: None)) – 运输矩阵

Returns:

梯度

Return type:

numpy.array 形状为 (n_p+nb_dummies, n_u)

参考文献

[12]

Peyré, Gabriel, Marco Cuturi, 和 Justin Solomon, “Gromov-Wasserstein 平均化核与距离矩阵。” 国际机器学习会议 (ICML). 2016.

ot.partial.gwloss_partial(C1, C2, T)

计算GW损失。

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.gwloss 替代。

Parameters:

• C1 (数组，形状（n_p，n_p）) – 源内（P）成本矩阵

• C2 (数组，形状 (n_u,n_u)) – 目标内部 (U) 成本矩阵

• T (数组，形状(n_p+nb_dummies, n_u) (默认: None)) – 运输矩阵

Return type:

GW损失

ot.partial.partial_gromov_wasserstein(C1, C2, p, q, m=None, nb_dummies=1, G0=None, thres=1, numItermax=1000, tol=1e-07, log=False, verbose=False, **kwargs)

解决部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\Omega\) 是熵正则化项， \(\Omega(\gamma) = \sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

• m 是要运输的质量量

该问题的公式已在 [29]中提出

注意

该函数将在不久的将来被弃用，请使用

请使用 ot.gromov.partial_gromov_wasserstein 代替。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• m (float, 可选) – 要运输的质量量（默认值: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\)）

• nb_dummies (int, 可选) – 要添加的虚拟点数（避免EMD求解器的不稳定性）

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• thres (float, 可选) – 当为0时，用于填充成本矩阵的梯度矩阵的分位数（默认值：1）

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止迭代的容忍度

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(partial_gromov_wasserstein(C1, C2, a, b),2)
array([[0.  , 0.25, 0.  , 0.  ],
       [0.25, 0.  , 0.  , 0.  ],
       [0.  , 0.  , 0.25, 0.  ],
       [0.  , 0.  , 0.  , 0.25]])
>>> np.round(partial_gromov_wasserstein(C1, C2, a, b, m=0.25),2)
array([[0.  , 0.  , 0.  , 0.  ],
       [0.  , 0.  , 0.  , 0.  ],
       [0.  , 0.  , 0.25, 0.  ],
       [0.  , 0.  , 0.  , 0.  ]])

参考文献

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.partial_gromov_wasserstein2(C1, C2, p, q, m=None, nb_dummies=1, G0=None, thres=1, numItermax=1000, tol=1e-07, log=False, verbose=False, **kwargs)

解决部分最优运输问题并返回部分Gromov-Wasserstein差异

该函数考虑以下问题：

\[GW = \min_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\Omega\) 是熵正则化项， \(\Omega(\gamma) = \sum_{i,j} \gamma_{i,j}\log(\gamma_{i,j})\)

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是样本权重

• m 是要运输的质量量

该问题的公式已在 [29]中提出

注意

该函数将在不久的将来被弃用，请使用

ot.gromov.partial_gromov_wasserstein2 替代。

Parameters:

• C1 (ndarray, shape (ns, ns)) – 源空间中的度量成本矩阵

• C2 (ndarray, shape (nt, nt)) – 目标空间中的度量成本矩阵

• p (ndarray, shape (ns,)) – 源空间中的分布

• q (ndarray, shape (nt,)) – 目标空间中的分布

• m (float, 可选) – 要运输的质量量（默认值: \(\min\{\|\mathbf{p}\|_1, \|\mathbf{q}\|_1\}\)）

• nb_dummies (int, 可选) – 要添加的虚拟点数（避免EMD求解器的不稳定性）

• G0 (ndarray, shape (ns, nt), optional) – 运输矩阵的初始化

• thres (float, 可选) – 当为0时，用于填充成本矩阵的梯度矩阵的分位数（默认值：1）

• numItermax (int, 可选) – 最大迭代次数

• tol (float, 可选) – 停止迭代的容忍度

• log (bool, optional) – 如果为 True，则返回日志

• verbose (bool, 可选) – 在迭代过程中打印信息

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• partial_gw_dist (float) – 部分GW差异

• log (dict) – 仅当 log 为 True 时返回的日志字典

示例

>>> import ot
>>> import scipy as sp
>>> a = np.array([0.25] * 4)
>>> b = np.array([0.25] * 4)
>>> x = np.array([1,2,100,200]).reshape((-1,1))
>>> y = np.array([3,2,98,199]).reshape((-1,1))
>>> C1 = sp.spatial.distance.cdist(x, x)
>>> C2 = sp.spatial.distance.cdist(y, y)
>>> np.round(partial_gromov_wasserstein2(C1, C2, a, b),2)
1.69
>>> np.round(partial_gromov_wasserstein2(C1, C2, a, b, m=0.25),2)
0.0

参考文献

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.partial_wasserstein(a, b, M, m=None, nb_dummies=1, log=False, **kwargs)

解决二次成本的部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源和目标不平衡分布

• m 是要运输的质量量

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 二次成本的成本矩阵

• m (float, 可选) – 要运输的质量量

• nb_dummies (int, 可选, 默认:1) – 要添加的储备点的数量（为了避免数值不稳定，如果出现错误，请增加其值）

• log (bool, 可选) – 如果为真，则记录日志

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> a = [.1, .2]
>>> b = [.1, .1]
>>> M = [[0., 1.], [2., 3.]]
>>> np.round(partial_wasserstein(a,b,M), 2)
array([[0.1, 0. ],
       [0. , 0.1]])
>>> np.round(partial_wasserstein(a,b,M,m=0.1), 2)
array([[0.1, 0. ],
       [0. , 0. ]])

参考文献

[28]

Caffarelli, L. A., & McCann, R. J. (2010) 最优运输和Monge-Ampere障碍问题中的自由边界。数学年鉴, 673-730.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

另请参见

ot.partial.partial_wasserstein_lagrange

部分瓦瑟斯坦（Wasserstein）与

正则化

ot.partial.entropic_partial_wasserstein

部分瓦瑟斯坦与 a

entropic

ot.partial.partial_wasserstein2(a, b, M, m=None, nb_dummies=1, log=False, **kwargs)

解决二次成本的部分最优传输问题并返回部分GW差异

该函数考虑以下问题：

\[\gamma = \min_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m &\leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源和目标不平衡分布

• m 是要运输的质量量

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 二次成本的成本矩阵

• m (float, 可选) – 要运输的质量量

• nb_dummies (int, 可选, 默认:1) – 要添加的储备点的数量（为了避免数值不稳定，如果出现错误，请增加其值）

• log (bool, 可选) – 如果为真，则记录日志

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• GW (float) – 部分GW差异

• log (dict) – 仅当 log 为 True 时返回日志字典

示例

>>> import ot
>>> a=[.1, .2]
>>> b=[.1, .1]
>>> M=[[0., 1.], [2., 3.]]
>>> np.round(partial_wasserstein2(a, b, M), 1)
0.3
>>> np.round(partial_wasserstein2(a,b,M,m=0.1), 1)
0.0

参考文献

[28]

Caffarelli, L. A., & McCann, R. J. (2010) 最优运输和Monge-Ampere障碍问题中的自由边界。数学年鉴, 673-730.

[29]

Chapel, L., Alaya, M., Gasso, G. (2020). “部分最优传输及其在正负标签学习中的应用”。NeurIPS.

ot.partial.partial_wasserstein_lagrange(a, b, M, reg_m=None, nb_dummies=1, log=False, **kwargs)

解决二次成本的部分最优运输问题并返回OT计划

该函数考虑以下问题：

\[\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, (\mathbf{M} - \lambda) \rangle_F\]

\[ \begin{align}\begin{aligned}s.t. \ \gamma \mathbf{1} &\leq \mathbf{a}\\ \gamma^T \mathbf{1} &\leq \mathbf{b}\\ \gamma &\geq 0\\ \mathbf{1}^T \gamma^T \mathbf{1} = m & \leq \min\{\|\mathbf{a}\|_1, \|\mathbf{b}\|_1\}\end{aligned}\end{align} \]

或者等价地（见 Chizat, L., Peyré, G., Schmitzer, B., & Vialard, F. X. (2018). 一种在最优传输与费舍尔–拉奥度量之间的插值距离。计算数学基础, 18(1), 1-44。）

\[ \begin{align}\begin{aligned}\gamma = \mathop{\arg \min}_\gamma \quad \langle \gamma, \mathbf{M} \rangle_F + \sqrt{\frac{\lambda}{2} (\|\gamma \mathbf{1} - \mathbf{a}\|_1 + \|\gamma^T \mathbf{1} - \mathbf{b}\|_1)}\\\text{s.t.} \ \gamma \geq 0\end{aligned}\end{align} \]

其中 :

• \(\mathbf{M}\) 是度量成本矩阵

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源和目标不平衡分布

• \(\lambda\) 是拉格朗日成本。调整其值可以实现要运输的给定质量 m

该问题的表述已在 [28]中提出

Parameters:

• a (np.ndarray (dim_a,)) – 未归一化的维度 dim_a 的直方图

• b (np.ndarray (dim_b,)) – 未归一化的维度 dim_b 的直方图

• M (np.ndarray (dim_a, dim_b)) – 二次成本的成本矩阵

• reg_m (浮动, 可选) – 拉格朗日成本

• nb_dummies (int, 可选, 默认:1) – 要添加的储备点的数量（为了避免数值不稳定，如果出现错误，请增加其值）

• log (bool, 可选) – 如果为真，则记录日志

• **kwargs (dict) – 参数可以直接传递给 emd 求解器

警告

当处理大量点时，EMD求解器可能会遇到一些不稳定性，特别是当与虚拟点相关的质量较大时。为了避免这些问题，请增加虚拟点的数量（允许在点之间更平滑地分配质量）。

Returns:

• gamma ((dim_a, dim_b) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 仅在 log 为 True 时返回的日志字典

示例

>>> import ot
>>> a = [.1, .2]
>>> b = [.1, .1]
>>> M = [[0., 1.], [2., 3.]]
>>> np.round(partial_wasserstein_lagrange(a,b,M), 2)
array([[0.1, 0. ],
       [0. , 0.1]])
>>> np.round(partial_wasserstein_lagrange(a,b,M,reg_m=2), 2)
array([[0.1, 0. ],
       [0. , 0. ]])

参考文献

[28]

Caffarelli, L. A., & McCann, R. J. (2010) 最优运输和Monge-Ampere障碍问题中的自由边界。数学年鉴, 673-730.

另请参见

ot.partial.partial_wasserstein

固定质量的部分瓦瑟斯坦距离