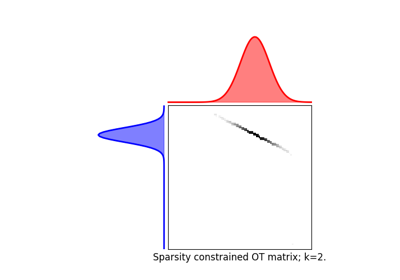
ot.smooth

平滑和稀疏（KL和L2正则化）以及稀疏约束的最优传输求解器。

实现： 平滑与稀疏的最优传输。 Mathieu Blondel, Vivien Seguy, Antoine Rolet。 发表于AISTATS 2018会议。 https://arxiv.org/abs/1710.06276

(原始代码来自 https://github.com/mblondel/smooth-ot/)

稀疏约束最优传输。刘, T., Puigcerver, J., & Blondel, M. (2023). 稀疏约束最优传输。第十一届国际学习表征会议 (ICLR) 论文集。 https://arxiv.org/abs/2209.15466

[17] Blondel, M., Seguy, V., & Rolet, A. (2018). 平滑与稀疏最优传输。第二十一届国际人工智能与统计会议（AISTATS）会议录。

[50] 刘, T., Puigcerver, J., & Blondel, M. (2023). 稀疏性约束的最优传输. 第十一届国际表示学习会议（ICLR）会议记录.

函数

ot.smooth.dual_obj_grad(alpha, beta, a, b, C, regul)

计算对偶目标的目标值和梯度。

Parameters:

• alpha (数组, 形状 = len(a))

• beta (array, shape = len(b)) – 当前双重潜能的迭代值。

• a (数组, 形状 = len(a))

• b (array, shape = len(b)) – 输入直方图（应该是非负的并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

Returns:

• obj (float) – 目标值（越高越好）。

• grad_alpha (array, shape = len(a)) – 关于 alpha 的梯度。

• grad_beta (array, shape = len(b)) – 关于 beta 的梯度。

ot.smooth.get_plan_from_dual(alpha, beta, C, regul)

从最优对偶潜力中获取最优运输计划。

Parameters:

• alpha (数组, 形状 = len(a))

• 贝塔 (数组, 形状 = len(b)) – 最优对偶势能。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

Returns:

T – 最优运输计划。

Return type:

数组，形状 = (len(a)， len(b))

ot.smooth.get_plan_from_semi_dual(alpha, b, C, regul)

从最优半对偶势中提取最优运输计划。

Parameters:

• alpha (array, shape = len(a)) – 最优半对偶势。

• b (array, shape = len(b)) – 第二个输入直方图（应该是非负的并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

Returns:

T – 最优运输计划。

Return type:

数组，形状 = (len(a)， len(b))

ot.smooth.projection_simplex(V, z=1, axis=None)

将 \(\mathbf{V}\) 投影到单纯形上，按 z 缩放

\[\begin{split}P\left(\mathbf{V}, z\right) = \mathop{\arg \min}_{\substack{\mathbf{y} >= 0 \\ \sum_i \mathbf{y}_i = z}} \quad \|\mathbf{y} - \mathbf{V}\|^2\end{split}\]

Parameters:

• V (ndarray, 2维)

• z (float 或 array) – 如果是数组，len(z) 必须与 \(\mathbf{V}\) 兼容

• axis (无 或 整数) –

  • axis=None: 通过 \(P(\mathbf{V}.\mathrm{ravel}(), z)\) 投影 \(\mathbf{V}\)

  • axis=1: 通过 \(P(\mathbf{V}_i, z_i)\) 投影每个 \(\mathbf{V}_i\)

  • axis=0: 通过 \(P(\mathbf{V}_{:, j}, z_j)\) 投影每个 \(\mathbf{V}_{:, j}\)

Returns:

投影

Return type:

ndarray, 形状 \(\mathbf{V}\).shape

ot.smooth.semi_dual_obj_grad(alpha, a, b, C, regul)

计算半对偶目标的目标值和梯度。

Parameters:

• alpha (array, shape = len(a)) – 当前半对偶势的迭代。

• a (数组, 形状 = len(a))

• b (array, shape = len(b)) – 输入直方图（应该是非负的并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 max_Omega(X) 方法。

Returns:

• obj (float) – 目标值（越高越好）。

• grad (array, shape = len(a)) – 关于 alpha 的梯度。

ot.smooth.smooth_ot_dual(a, b, M, reg, reg_type='l2', method='L-BFGS-B', stopThr=1e-09, numItermax=500, verbose=False, log=False, max_nz=None)

求解对偶中的正则化OT问题并返回OT矩阵

该函数求解平滑松弛对偶形式 (7) 在 [17]:

\[\max_{\alpha,\beta}\quad \mathbf{a}^T\alpha + \mathbf{b}^T\beta - \sum_j \delta_\Omega \left(\alpha+\beta_j-\mathbf{m}_j \right)\]

其中 :

• \(\mathbf{m}_j\) 是成本矩阵的第 j 列

• \(\delta_\Omega\) 是正则化项 \(\Omega\) 的凸共轭

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重（总和为1）

OT矩阵可以从\(\delta_\Omega\)的梯度中重建（见[17]命题1）。优化算法使用梯度下降（默认使用L-BFGS）。

Parameters:

• a (np.ndarray (ns,)) – 源域中的样本权重

• b (np.ndarray (nt,) 或 np.ndarray (nt,nbb)) - 目标域中的样本，如果\(\mathbf{b}\)是矩阵，则计算具有多个目标和固定\(\mathbf{M}\)的Sinkhorn（返回OT损失 + 对数中的对偶变量）

• M (np.ndarray (ns,nt)) – 损失矩阵

• reg (float) – 正则化项 >0

• reg_type (str) –

  正则化类型，可以为以下值（默认 =’l2’）：

  • ’kl’ : Kullback Leibler (~ 用于Sinkhorn的负熵 [2])

  • ’l2’ : 平方欧几里得正则化

  • ’sparsity_constrained’ : 稀疏约束正则化 [50]

• max_nz (int 或 None, 可选。在reg_type = 'sparsity_constrained'的情况下使用，指定每列的最大非零项数量;) – 对于其他正则化类型不使用。

• method (str) – 用于 scipy.optimize.minimize 的求解器

• numItermax (int, 可选) – 最大迭代次数

• stopThr (float, 可选) – 错误的停止阈值 (>0)

• verbose (bool, 可选) – 在迭代过程中打印信息

• log (bool, 可选) – 如果为真，则记录日志

Returns:

• gamma ((ns, nt) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 只有在参数中log==True时返回日志字典

参考文献

[2]

13. Cuturi, Sinkhorn距离：最优运输的快速计算，《神经信息处理系统进展》（NIPS）26，2013

[17]

Blondel, M., Seguy, V., & Rolet, A. (2018). 平滑与稀疏最优传输. 第二十一届人工智能与统计国际会议会议录 (AISTATS).

[50]

Liu, T., Puigcerver, J., & Blondel, M. (2023). 稀疏受限的最优传输。第十一届国际学习表征会议（ICLR）论文集。

另请参见

ot.lp.emd

未正则化的OT

ot.sinhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

使用 ot.smooth.smooth_ot_dual 的示例

平滑和稀疏OT示例

平滑与稀疏OT示例

ot.smooth.smooth_ot_semi_dual(a, b, M, reg, reg_type='l2', max_nz=None, method='L-BFGS-B', stopThr=1e-09, numItermax=500, verbose=False, log=False)

求解半对偶中的正则化OT问题并返回OT矩阵

该函数求解平滑放松的对偶形式 (10) 在 [17]:

\[\max_{\alpha}\quad \mathbf{a}^T\alpha- \mathrm{OT}_\Omega^*(\alpha, \mathbf{b})\]

其中 :

\[\mathrm{OT}_\Omega^*(\alpha,b)=\sum_j \mathbf{b}_j\]

• \(\mathbf{m}_j\) 是成本矩阵的第 j 列

• \(\mathrm{OT}_\Omega^*(\alpha,b)\) 在公式 (9) 中定义于 [17]

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重（总和为1）

OT 矩阵可以使用 [17] 命题 2 进行重构。优化算法使用梯度下降法（默认使用 L-BFGS）。

Parameters:

• a (np.ndarray (ns,)) – 源域中的样本权重

• b (np.ndarray (nt,) 或 np.ndarray (nt,nbb)) – 目标域中的样本，计算具有多个目标和固定:math:mathbf{M} 的sinkhorn，如果 \(\mathbf{b}\) 是矩阵（返回OT损失 + 对偶变量的对数）

• M (np.ndarray (ns,nt)) – 损失矩阵

• reg (float) – 正则化项 >0

• reg_type (str) –

  正则化类型，可以为以下值（默认 =’l2’）：

  • ’kl’ : Kullback Leibler (~ 用于Sinkhorn的负熵 [2])

  • ’l2’ : 平方欧几里得正则化

  • ’sparsity_constrained’ : 稀疏约束正则化 [50]

• max_nz (int 或 None, 可选。在reg_type = 'sparsity_constrained'的情况下使用，指定每列的最大非零项数量;) – 对于其他正则化类型不使用。

• method (str) – 用于 scipy.optimize.minimize 的求解器

• numItermax (int, 可选) – 最大迭代次数

• stopThr (float, 可选) – 错误的停止阈值 (>0)

• verbose (bool, 可选) – 在迭代过程中打印信息

• log (bool, 可选) – 如果为真，则记录日志

Returns:

• gamma ((ns, nt) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 只有在参数中log==True时返回日志字典

参考文献

[2]

13. Cuturi, Sinkhorn距离：最优运输的快速计算，《神经信息处理系统进展》（NIPS）26，2013

[17]

Blondel, M., Seguy, V., & Rolet, A. (2018). 平滑与稀疏最优传输. 第二十一届人工智能与统计国际会议会议录 (AISTATS).

[50]

Liu, T., Puigcerver, J., & Blondel, M. (2023). 稀疏受限的最优传输。第十一届国际学习表征会议（ICLR）论文集。

另请参见

ot.lp.emd

未正则化的OT

ot.sinhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.smooth.solve_dual(a, b, C, regul, method='L-BFGS-B', tol=0.001, max_iter=500, verbose=False)

求解“平滑”的对偶目标。

Parameters:

• a (数组, 形状 = (len(a), ))

• b (array, shape = (len(b), )) – 输入的直方图（应该是非负的，并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

• 方法 (str) – 使用的求解器 (传递给 scipy.optimize.minimize).

• tol (float) – 容差参数。

• max_iter (int) – 最大迭代次数。

Returns:

• alpha (数组，形状 = (len(a), ))

• beta (数组，形状 = (len(b), )) – 对偶势。

ot.smooth.solve_semi_dual(a, b, C, regul, method='L-BFGS-B', tol=0.001, max_iter=500, verbose=False)

求解“平滑”的半对偶目标。

Parameters:

• a (数组, 形状 = (len(a), ))

• b (array, shape = (len(b), )) – 输入的直方图（应该是非负的，并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 max_Omega(X) 方法。

• 方法 (str) – 使用的求解器 (传递给 scipy.optimize.minimize).

• tol (float) – 容差参数。

• max_iter (int) – 最大迭代次数。

Returns:

alpha – 半双重势能。

Return type:

数组，形状 = (len(a), )

类

class ot.smooth.NegEntropy(gamma=1.0)

负熵正则化

Omega(T)

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega(X)

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(X, b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.Regularization(gamma=1.0)

正则化对象的基类

备注

这个类并不打算直接使用，而是显然用于真正的正则化实现。

Omega()

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega()

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.SparsityConstrained(max_nz, gamma=1.0)

带稀疏约束的平方L2正则化

Omega(T)

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega(X)

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(X, b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.SquaredL2(gamma=1.0)

平方L2正则化

Omega(T)

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega(X)

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(X, b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.NegEntropy(gamma=1.0)

负熵正则化

Omega(T)

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega(X)

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(X, b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.Regularization(gamma=1.0)

正则化对象的基类

备注

这个类并不打算直接使用，而是显然用于真正的正则化实现。

Omega()

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega()

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.SparsityConstrained(max_nz, gamma=1.0)

带稀疏约束的平方L2正则化

Omega(T)

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega(X)

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(X, b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

class ot.smooth.SquaredL2(gamma=1.0)

平方L2正则化

Omega(T)

计算正则化项。

Parameters:

T (array, shape = len(a) x len(b)) – 输入数组。

Returns:

value – 正则化项。

Return type:

float

delta_Omega(X)

计算 \(\delta_\Omega(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\delta_\Omega(\mathbf{x}) = \sup_{\mathbf{y} >= 0} \ \mathbf{y}^T \mathbf{x} - \Omega(\mathbf{y})\]

Parameters:

X (array, shape = (len(a), len(b))) – 输入数组。

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \delta_\Omega(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \delta_\Omega(\mathbf{X}_{:, j})\)

max_Omega(X, b)

计算 \(\mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\) 对于每个 \(\mathbf{X}_{:, j}\)。

\[\mathrm{max}_{\Omega, j}(\mathbf{x}) = \sup_{\substack{\mathbf{y} >= 0 \ \sum_i \mathbf{y}_i = 1}} \mathbf{y}^T \mathbf{x} - \frac{1}{\mathbf{b}_j} \Omega(\mathbf{b}_j \mathbf{y})\]

Parameters:

• X (数组, 形状 = (len(a), len(b))) – 输入数组。

• b (数组, 形状 = (len(b), ))

Returns:

• v (数组, (len(b), )) – 值: \(\mathbf{v}_j = \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

• G (数组, (len(a), len(b))) – 梯度: \(\mathbf{G}_{:, j} = \nabla \mathrm{max}_{\Omega, j}(\mathbf{X}_{:, j})\)

ot.smooth.dual_obj_grad(alpha, beta, a, b, C, regul)

计算对偶目标的目标值和梯度。

Parameters:

• alpha (数组, 形状 = len(a))

• beta (array, shape = len(b)) – 当前双重潜能的迭代值。

• a (数组, 形状 = len(a))

• b (array, shape = len(b)) – 输入直方图（应该是非负的并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

Returns:

• obj (float) – 目标值（越高越好）。

• grad_alpha (array, shape = len(a)) – 关于 alpha 的梯度。

• grad_beta (array, shape = len(b)) – 关于 beta 的梯度。

ot.smooth.get_plan_from_dual(alpha, beta, C, regul)

从最优对偶潜力中获取最优运输计划。

Parameters:

• alpha (数组, 形状 = len(a))

• 贝塔 (数组, 形状 = len(b)) – 最优对偶势能。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

Returns:

T – 最优运输计划。

Return type:

数组，形状 = (len(a)， len(b))

ot.smooth.get_plan_from_semi_dual(alpha, b, C, regul)

从最优半对偶势中提取最优运输计划。

Parameters:

• alpha (array, shape = len(a)) – 最优半对偶势。

• b (array, shape = len(b)) – 第二个输入直方图（应该是非负的并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

Returns:

T – 最优运输计划。

Return type:

数组，形状 = (len(a)， len(b))

ot.smooth.projection_simplex(V, z=1, axis=None)

将 \(\mathbf{V}\) 投影到单纯形上，按 z 缩放

\[\begin{split}P\left(\mathbf{V}, z\right) = \mathop{\arg \min}_{\substack{\mathbf{y} >= 0 \\ \sum_i \mathbf{y}_i = z}} \quad \|\mathbf{y} - \mathbf{V}\|^2\end{split}\]

Parameters:

• V (ndarray, 2维)

• z (float 或 array) – 如果是数组，len(z) 必须与 \(\mathbf{V}\) 兼容

• axis (无 或 整数) –

  • axis=None: 通过 \(P(\mathbf{V}.\mathrm{ravel}(), z)\) 投影 \(\mathbf{V}\)

  • axis=1: 通过 \(P(\mathbf{V}_i, z_i)\) 投影每个 \(\mathbf{V}_i\)

  • axis=0: 通过 \(P(\mathbf{V}_{:, j}, z_j)\) 投影每个 \(\mathbf{V}_{:, j}\)

Returns:

投影

Return type:

ndarray, 形状 \(\mathbf{V}\).shape

ot.smooth.semi_dual_obj_grad(alpha, a, b, C, regul)

计算半对偶目标的目标值和梯度。

Parameters:

• alpha (array, shape = len(a)) – 当前半对偶势的迭代。

• a (数组, 形状 = len(a))

• b (array, shape = len(b)) – 输入直方图（应该是非负的并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 max_Omega(X) 方法。

Returns:

• obj (float) – 目标值（越高越好）。

• grad (array, shape = len(a)) – 关于 alpha 的梯度。

ot.smooth.smooth_ot_dual(a, b, M, reg, reg_type='l2', method='L-BFGS-B', stopThr=1e-09, numItermax=500, verbose=False, log=False, max_nz=None)

求解对偶中的正则化OT问题并返回OT矩阵

该函数求解平滑松弛对偶形式 (7) 在 [17]:

\[\max_{\alpha,\beta}\quad \mathbf{a}^T\alpha + \mathbf{b}^T\beta - \sum_j \delta_\Omega \left(\alpha+\beta_j-\mathbf{m}_j \right)\]

其中 :

• \(\mathbf{m}_j\) 是成本矩阵的第 j 列

• \(\delta_\Omega\) 是正则化项 \(\Omega\) 的凸共轭

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重（总和为1）

OT矩阵可以从\(\delta_\Omega\)的梯度中重建（见[17]命题1）。优化算法使用梯度下降（默认使用L-BFGS）。

Parameters:

• a (np.ndarray (ns,)) – 源域中的样本权重

• b (np.ndarray (nt,) 或 np.ndarray (nt,nbb)) - 目标域中的样本，如果\(\mathbf{b}\)是矩阵，则计算具有多个目标和固定\(\mathbf{M}\)的Sinkhorn（返回OT损失 + 对数中的对偶变量）

• M (np.ndarray (ns,nt)) – 损失矩阵

• reg (float) – 正则化项 >0

• reg_type (str) –

  正则化类型，可以为以下值（默认 =’l2’）：

  • ’kl’ : Kullback Leibler (~ 用于Sinkhorn的负熵 [2])

  • ’l2’ : 平方欧几里得正则化

  • ’sparsity_constrained’ : 稀疏约束正则化 [50]

• max_nz (int 或 None, 可选。在reg_type = 'sparsity_constrained'的情况下使用，指定每列的最大非零项数量;) – 对于其他正则化类型不使用。

• method (str) – 用于 scipy.optimize.minimize 的求解器

• numItermax (int, 可选) – 最大迭代次数

• stopThr (float, 可选) – 错误的停止阈值 (>0)

• verbose (bool, 可选) – 在迭代过程中打印信息

• log (bool, 可选) – 如果为真，则记录日志

Returns:

• gamma ((ns, nt) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 只有在参数中log==True时返回日志字典

参考文献

[2]

13. Cuturi, Sinkhorn距离：最优运输的快速计算，《神经信息处理系统进展》（NIPS）26，2013

[17]

Blondel, M., Seguy, V., & Rolet, A. (2018). 平滑与稀疏最优传输. 第二十一届人工智能与统计国际会议会议录 (AISTATS).

[50]

Liu, T., Puigcerver, J., & Blondel, M. (2023). 稀疏受限的最优传输。第十一届国际学习表征会议（ICLR）论文集。

另请参见

ot.lp.emd

未正则化的OT

ot.sinhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.smooth.smooth_ot_semi_dual(a, b, M, reg, reg_type='l2', max_nz=None, method='L-BFGS-B', stopThr=1e-09, numItermax=500, verbose=False, log=False)

求解半对偶中的正则化OT问题并返回OT矩阵

该函数求解平滑放松的对偶形式 (10) 在 [17]:

\[\max_{\alpha}\quad \mathbf{a}^T\alpha- \mathrm{OT}_\Omega^*(\alpha, \mathbf{b})\]

其中 :

\[\mathrm{OT}_\Omega^*(\alpha,b)=\sum_j \mathbf{b}_j\]

• \(\mathbf{m}_j\) 是成本矩阵的第 j 列

• \(\mathrm{OT}_\Omega^*(\alpha,b)\) 在公式 (9) 中定义于 [17]

• \(\mathbf{a}\) 和 \(\mathbf{b}\) 是源权重和目标权重（总和为1）

OT 矩阵可以使用 [17] 命题 2 进行重构。优化算法使用梯度下降法（默认使用 L-BFGS）。

Parameters:

• a (np.ndarray (ns,)) – 源域中的样本权重

• b (np.ndarray (nt,) 或 np.ndarray (nt,nbb)) – 目标域中的样本，计算具有多个目标和固定:math:mathbf{M} 的sinkhorn，如果 \(\mathbf{b}\) 是矩阵（返回OT损失 + 对偶变量的对数）

• M (np.ndarray (ns,nt)) – 损失矩阵

• reg (float) – 正则化项 >0

• reg_type (str) –

  正则化类型，可以为以下值（默认 =’l2’）：

  • ’kl’ : Kullback Leibler (~ 用于Sinkhorn的负熵 [2])

  • ’l2’ : 平方欧几里得正则化

  • ’sparsity_constrained’ : 稀疏约束正则化 [50]

• max_nz (int 或 None, 可选。在reg_type = 'sparsity_constrained'的情况下使用，指定每列的最大非零项数量;) – 对于其他正则化类型不使用。

• method (str) – 用于 scipy.optimize.minimize 的求解器

• numItermax (int, 可选) – 最大迭代次数

• stopThr (float, 可选) – 错误的停止阈值 (>0)

• verbose (bool, 可选) – 在迭代过程中打印信息

• log (bool, 可选) – 如果为真，则记录日志

Returns:

• gamma ((ns, nt) ndarray) – 给定参数的最优运输矩阵

• log (dict) – 只有在参数中log==True时返回日志字典

参考文献

[2]

13. Cuturi, Sinkhorn距离：最优运输的快速计算，《神经信息处理系统进展》（NIPS）26，2013

[17]

Blondel, M., Seguy, V., & Rolet, A. (2018). 平滑与稀疏最优传输. 第二十一届人工智能与统计国际会议会议录 (AISTATS).

[50]

Liu, T., Puigcerver, J., & Blondel, M. (2023). 稀疏受限的最优传输。第十一届国际学习表征会议（ICLR）论文集。

另请参见

ot.lp.emd

未正则化的OT

ot.sinhorn

熵正则化最优传输

ot.optim.cg

通用正则化OT

ot.smooth.solve_dual(a, b, C, regul, method='L-BFGS-B', tol=0.001, max_iter=500, verbose=False)

求解“平滑”的对偶目标。

Parameters:

• a (数组, 形状 = (len(a), ))

• b (array, shape = (len(b), )) – 输入的直方图（应该是非负的，并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 delta_Omega(X) 方法。

• 方法 (str) – 使用的求解器 (传递给 scipy.optimize.minimize).

• tol (float) – 容差参数。

• max_iter (int) – 最大迭代次数。

Returns:

• alpha (数组，形状 = (len(a), ))

• beta (数组，形状 = (len(b), )) – 对偶势。

ot.smooth.solve_semi_dual(a, b, C, regul, method='L-BFGS-B', tol=0.001, max_iter=500, verbose=False)

求解“平滑”的半对偶目标。

Parameters:

• a (数组, 形状 = (len(a), ))

• b (array, shape = (len(b), )) – 输入的直方图（应该是非负的，并且总和为1）。

• C (array, shape = (len(a), len(b))) – 地面成本矩阵。

• regul (正则化对象) – 应该实现一个 max_Omega(X) 方法。

• 方法 (str) – 使用的求解器 (传递给 scipy.optimize.minimize).

• tol (float) – 容差参数。

• max_iter (int) – 最大迭代次数。

Returns:

alpha – 半双重势能。

Return type:

数组，形状 = (len(a), )