快速入门指南
在以下内容中,我们提供了一些关于针对与最优传输(OT)和机器学习相关的不同问题该使用哪些函数和类的指引。我们会在可能的情况下引用文档中的具体例子,这些例子也可以在POT Github上作为笔记本获得。
注意
从版本0.8开始,POT提供了一个后端,可以自动解决一些与用户使用的工具箱(numpy/torch/jax)无关的OT问题。我们在后端部分中提供了关于哪些函数兼容的讨论。
为什么选择最优传输?
何时使用OT
最优传输(OT)是一个数学问题,由Gaspard Monge在1781年提出,旨在寻找在两个分布之间移动质量的最有效方式。将单位质量在两个位置之间移动的成本称为基础成本,目标是最小化将一个质量分布移动到另一个质量分布的整体成本。该优化问题可以用两个分布\(\mu_s\)和\(\mu_t\)表示。
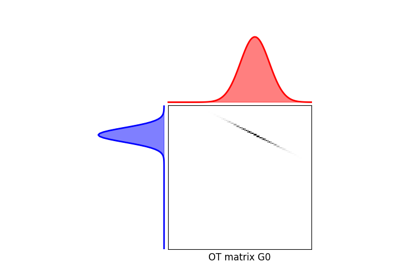
其中 \(c(\cdot,\cdot)\) 是基础成本,约束条件 \(m \# \mu_s = \mu_t\) 确保 \(\mu_s\) 被完全运输到 \(\mu_t\)。由于这个约束,这个问题特别难以解决,并且在实践中(在离散分布上)被一个更易解决的线性程序所替代。它对应于Kantorovitch形式,其中Monge映射 \(m\) 被一个联合分布(在下一节中表示的OT矩阵)所替代(见 解决最优运输问题)。
从上面的优化问题中我们可以看到,OT解决方案在实际应用中有两个主要方面:
最优值(Wasserstein 距离):衡量分布之间的相似性。
最优映射(Monge映射,OT矩阵):查找分布之间的对应关系。
在第一种情况下,OT可用于测量分布(或数据集)之间的相似性,在这种情况下使用的是Wasserstein距离(问题的最优值)。在第二种情况下,人们可能对质量在分布之间移动的方式(映射)感兴趣。然后可以使用这个映射在分布之间转移知识。
分布之间的Wasserstein距离
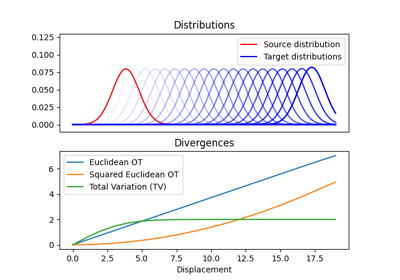
OT通常用于测量分布之间的相似性,尤其是当它们不共享相同的支持时。当分布之间的支持是不相交的,基于OT的Wasserstein距离相较于流行的f-散度,如流行的Kullback-Leibler散度、Jensen-Shannon散度和总变差距离,表现得更好。对于数据科学应用来说,特别有趣的是可以计算Wasserstein距离的有意义的次梯度。正因如此,它成为了一个非常有效的工具,适用于需要测量和优化经验分布之间相似性的机器学习应用。
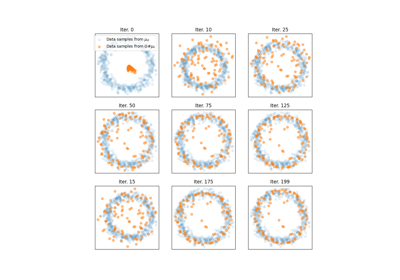
许多贡献利用这种方法是在机器学习(ML)文献中。例如 OT 被用于训练 生成对抗网络(GANs),以克服消失梯度问题。它还被用于寻找数据集的 判别 或 鲁棒 子空间。Wasserstein 距离也被用来测量 文档的词嵌入之间的相似性 或者 信号 或 光谱 之间的相似性。
用于映射估计的OT
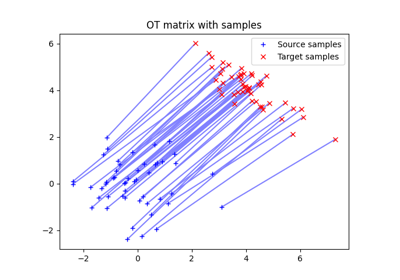
OT问题的一个很有趣的方面是OT映射本身。当计算离散分布之间的最优传输时,一个输出是OT矩阵,它将为您提供每个分布中样本之间的对应关系。
该对应关系是根据OT标准进行估算的,且以无监督的方式发现,这使其在数据集之间的迁移问题上非常有趣。它已被用于执行图像之间的颜色转移或在领域适应的背景下使用。更近期的应用包括使用OT的扩展(Gromov-Wasserstein)来找到词嵌入中语言之间的对应关系。
何时使用POT
POT的主要目标是为机器学习背景下快速增长的OT领域提供OT求解器。为此,我们实现了一些已在研究论文中提出的求解器。这样做我们旨在促进可重复的研究并推动新的发展。
POT 的一个非常重要的方面是其易于扩展的能力。比如,我们提供了一个非常通用的 OT 求解器 ot.optim.cg,可以解决具有任何平滑/连续正则项的 OT 问题,这使其特别适合研究目的。注意,这个通用求解器已被用于解决图拉普拉斯正则化 OT 和 Gromov Wasserstein [30]。
何时不使用POT
虽然POT在我们所知的范围内是最有效的精确OT求解器之一,但它并没有被设计用于处理大规模的OT问题。例如,OT问题的内存成本总是\(\mathcal{O}(n^2)\),因为需要计算成本矩阵。精确求解器的时间复杂度是\(\mathcal{O}(n^3\log(n))\),而Sinkhorn求解器的证明接近\(\mathcal{O}(n^2)\),这对于非常大规模的求解器来说仍然太复杂。
如果您需要解决样本数量较大的OT问题,我们建议使用熵正则化和Sinkhorn的内存高效实现,如GeomLoss中所提议的。这种实现与Pytorch兼容,可以处理大量样本。另一个估计非常大量样本的Wasserstein距离的方法是使用来自Wasserstein GAN的技巧,通过神经网络估计对偶变量来解决对偶中的问题。请注意,在这种情况下,您仅仅是在解决Wasserstein距离的一个近似,因为对偶上的1-Lipschitz约束无法被准确施加(通过过滤阈值或正则化进行近似)。最后,请注意,为了避免解决大规模OT问题,最近一些方法最小化了在小批量上的期望Wasserstein距离,这与Wasserstein不同,但具有更好的计算和统计性质。
最优传输和瓦瑟斯坦距离
注意
在POT中,解决OT或正则化OT问题的大多数函数有两个版本,返回OT矩阵或最优解的值。例如 ot.emd 返回OT矩阵,而 ot.emd2 返回Wasserstein距离。这种方法在所有返回OT矩阵的求解器中得到了实际应用(甚至Gromov-Wasserstein)。
解决最优运输
离散分布之间的最优传输问题通常表示为
其中:
\(M\in\mathbb{R}_+^{m\times n}\) 是定义从箱子 \(a_i\) 移动质量到箱子 \(b_j\) 的度量成本矩阵。
\(a\) 和 \(b\) 是定义在单纯形上的直方图(正值,和为1),表示源分布和目标分布中每个样本的权重。
解决上述线性程序可以使用函数 ot.emd,该函数将返回最优运输矩阵 \(\gamma^*\):
# a and b are 1D histograms (sum to 1 and positive)
# M is the ground cost matrix
T = ot.emd(a, b, M) # exact linear program
解决OT问题的方法是网络单纯形法。它是用C语言实现的,来源于[1]。它的复杂度是\(O(n^3)\),但是求解器非常高效,并利用了解的稀疏性。
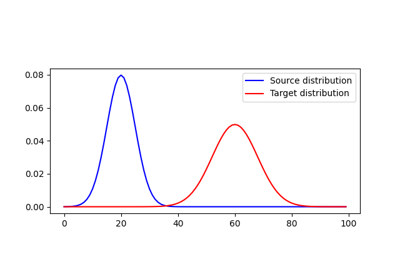
使用ot.emd的示例
计算Wasserstein距离
OT解决方案的价值通常比OT矩阵更有趣:
它可以从已经估计的OT矩阵计算得出,使用 np.sum(T*M) 或直接使用函数 ot.emd2。
# a and b are 1D histograms (sum to 1 and positive)
# M is the ground cost matrix
W = ot.emd2(a, b, M) # Wasserstein distance / EMD value
请注意,已知的Wasserstein距离在分布a和b之间被定义为
\[ \begin{align}\begin{aligned}W_p(a,b)=(\min_{\gamma \in \mathbb{R}_+^{m\times n}} \sum_{i,j}\gamma_{i,j}\|x_i-y_j\|_p)^\frac{1}{p}\\\text{满足} \gamma 1 = a; \gamma^T 1= b; \gamma\geq 0\end{aligned}\end{align} \]
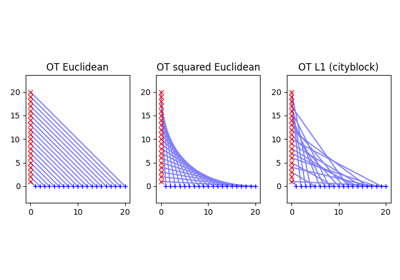
这意味着如果你想计算 \(W_2\),你需要计算 ot.emd2 的平方根,当提供 M = ot.dist(xs, xt) 时,默认使用平方欧几里得距离。计算 \(W_1\) Wasserstein 距离可以直接使用 ot.emd2,当提供 M = ot.dist(xs, xt, metric='euclidean') 以使用欧几里得距离。
使用ot.emd2的示例
特殊情况
请注意,OT问题和相应的Wasserstein距离在某些特定情况下可以非常高效地计算。
例如,当样本是一维时,可以通过简单的排序在
\(O(n\log(n))\)中解决OT问题。在这种情况下,我们提供
函数 ot.emd_1d 和 ot.emd2_1d 分别返回OT
矩阵和值。请注意,由于解非常稀疏,sparse
参数在ot.emd_1d中允许解决并返回非常大的问题的解。请注意,为了直接计算一维中的\(W_p\)
Wasserstein距离,我们提供函数 ot.wasserstein_1d,它
将p作为参数。
另一个用于估计OT和Monge映射的特殊情况是高斯分布之间。在这种情况下,Remark 2.29中提供了一个闭合形式的解决方案,见[15],并且Monge映射是一个仿射函数,也可以从源分布和目标分布的协方差和均值中计算。在有限样本数据集假设为高斯的情况下,我们提供ot.gaussian.bures_wasserstein_mapping,返回Monge映射的参数。
正则化最优传输
最近的发展表明,正则化最优运输(OT)在计算和统计属性方面都引起了兴趣。 我们在这一部分讨论可以表达为正则化OT问题的内容。
其中 :
\(M\in\mathbb{R}_+^{m\times n}\) 是定义从箱 \(a_i\) 移动质量到箱 \(b_j\) 的度量成本矩阵。
\(a\) 和 \(b\) 是直方图(正值,总和为1),表示源分布和目标分布中每个样本的权重。
\(\Omega\) 是正则化项。
我们将在下面讨论可以根据正则化项使用的特定算法。
熵正则化的OT
这是最常用的最优传输正则化。它在机器学习社区中由Marco Cuturi在他的开创性论文中提出[2]。该正则化的表达式如下
上述正则化项在优化问题中的使用有着非常强的影响。首先,它使得问题光滑,这导致了新的优化程序,如著名的Sinkhorn算法 [2] 或 L-BFGS(见 ot.smooth)。接下来,它使得问题严格凸,意味着将会有一个唯一的解。最后,得到的优化问题的解可以表达为:
其中 \(u\) 和 \(v\) 是向量,\(K=\exp(-M/\lambda)\),其中\(\exp\) 是逐个分量计算的。为了求解优化问题,可以使用一种替代的投影算法,称为 Sinkhorn-Knopp,对于大的正则化值,这种算法可能非常高效。
Sinkhorn-Knopp 算法在 ot.sinkhorn 和 ot.sinkhorn2 中实现,分别返回 OT 矩阵和线性项的值。请注意,上述方程中的正则化参数 \(\lambda\) 是通过参数 reg 传递给这些函数的。
>>> import ot
>>> a = [.5, .5]
>>> b = [.5, .5]
>>> M = [[0., 1.], [1., 0.]]
>>> ot.sinkhorn(a, b, M, 1)
array([[ 0.36552929, 0.13447071],
[ 0.13447071, 0.36552929]])
关于所使用算法的更多细节在以下说明中给出。
注意
解决熵正则化OT的主要函数是 ot.sinkhorn。这个函数是一个包装器,参数 method 允许您选择用于解决问题的实际算法:
method='sinkhorn'调用ot.bregman.sinkhorn_knopp经典算法 [2]。method='sinkhorn_log'调用ot.bregman.sinkhorn_log的 sinkhorn 算法在对数空间 [2],该算法更稳定,但在 numpy 中可能会较慢,因为 logsumexp 并没有并行实现。 这是推荐的求解器,适用于需要 可微分性且迭代次数较少的应用。method='sinkhorn_stabilized'调用ot.bregman.sinkhorn_stabilized算法的日志稳定版本 [9].method='sinkhorn_epsilon_scaling'调用ot.bregman.sinkhorn_epsilon_scaling算法的epsilon缩放版本 [9]。method='greenkhorn'调用ot.bregman.greenkhorn贪婪的Sinkhorn版本的算法 [22]。method='screenkhorn'调用ot.bregman.screenkhorn算法的筛选Sinkhorn版本 [26]。
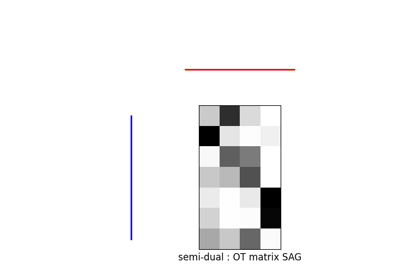
除了所有这些Sinkhorn的变体,我们还有另一种实现,解决在ot.smooth中的光滑对偶或半对偶问题。这个求解器使用scipy.optimize.minimize
函数利用L-BFGS-B算法解决光滑问题。要使用
这个求解器,请使用函数ot.smooth.smooth_ot_dual或
ot.smooth.smooth_ot_semi_dual,并将参数reg_type='kl'设置为
选择熵/Kullback-Leibler正则化。
选择一个Sinkhorn求解器
默认情况下,当使用一个不太小的正则化参数时,默认的 Sinkhorn 求解器应该足够。如果您需要使用较小的正则化来获得更尖锐的 OT 矩阵,您应该使用
ot.bregman.sinkhorn_stabilized 求解器,以避免数值错误。这个求解器在实践中可能非常慢,甚至可能在有限的时间内无法收敛到合理的 OT 矩阵。这就是为什么
ot.bregman.sinkhorn_epsilon_scaling 依赖于迭代正则化值(并使用热启动)有时能够导致更好的解决方案。请注意,Sinkhorn 的贪婪版本
ot.bregman.greenkhorn 也可以带来加速,而 Sinkhorn 的筛选版本 ot.bregman.screenkhorn 旨在提供 Sinkhorn 问题的快速近似。对于使用 GPU 和小迭代次数的梯度计算,我们强烈推荐
ot.bregman.sinkhorn_log 求解器,因为它无需检查数值问题。
最近,Genevay 等人 [23] 引入了 Sinkhorn 散度,它基于熵正则化,用于计算经验分布之间的快速且可微分的几何散度。请注意,我们提供了一个直接计算经验分布的 Sinkhorn 散度的函数(无需预计算 M 矩阵),该函数位于 ot.bregman.empirical_sinkhorn_divergence。类似地,可以分别使用 ot.bregman.empirical_sinkhorn 和 ot.bregman.empirical_sinkhorn2 计算经验分布的 OT 矩阵和损失。
最后请注意,我们在 ot.stochastic 中提供了多个随机求解器的实现,用于熵正则化OT [18] [19]。这些纯Python的实现虽然没有针对速度进行优化,但提供了在 [18] [19] 中算法的稳健实现。
使用 ot.sinkhorn 的示例
ot.sinkhorn2的使用示例
其他正则化
虽然熵最优传输是实践中最常见和被青睐的,但还存在其他类型的正则化。我们在POT中提供了两种特定的求解器用于其他正则化项,即二次正则化和组Lasso正则化。但我们还在 ot.optim 中提供了两种通用求解器,允许在实践中解决任何平滑正则化。
二次正则化
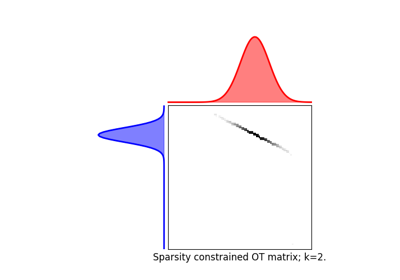
我们可以解决的第一个一般正则化项是以下形式的二次正则化
这个正则化项的作用类似于熵正则化,通过强化OT矩阵,但它保持了一定的稀疏性,而这种稀疏性在熵正则化中一旦\(\lambda>0\)就会丧失[17]。这个问题可以通过POT与ot.smooth中的求解器来解决,更具体地说是使用函数ot.smooth.smooth_ot_dual或ot.smooth.smooth_ot_semi_dual,并使用参数reg_type='l2'来选择二次正则化。
二次正则化的使用示例
组Lasso正则化
近年来使用的另一种正则化方法是组Lasso正则化
其中 \(\mathcal{G}\) 包含了OT矩阵中互不重叠的线组。 在[5]中提出的这种正则化促进了组级别的稀疏性,例如,会迫使目标样本从少量组中获取质量。 注意,精确的OT解已经是稀疏的,因此如果不与熵正则化结合使用,这种正则化是没有意义的。 根据p和q的选择,可以使用不同的方法来解决问题。 当q=1且p<1时,该问题是非凸的,但可以使用高效的上界最小化方法通过ot.sinkhorn_lpl1_mm解决。 当q=2且p=1时,我们恢复了凸组套索,并提供使用广义条件梯度算法的求解器[7],在函数ot.da.sinkhorn_l1l2_gl中。
组Lasso正则化的示例
通用求解器
最后我们在POT中提出了通用求解器,可以用于解决任何正则化,只要您能够提供一个计算正则化的函数和一个计算其梯度(或次梯度)的函数。
为了解决
您可以使用函数 ot.optim.cg,该函数将使用条件梯度,如在 [6] 中提出的。您需要将正则化函数作为参数 f 提供,并将其梯度作为参数 df。请注意,条件梯度依赖于通过使用精确的 ot.emd 迭代解决问题的线性化,因此在实践中可能会相当缓慢。然而,作为一种内部点算法,它始终返回一个不会违反边际的运输矩阵。
提出了一种通用求解器来解决此问题:
其中 \(\Omega_e\) 是熵正则化。在这种情况下,我们使用在 ot.optim.gcg 中实现的广义条件梯度 [7],它不对熵项进行线性化,而是依赖于 ot.sinkhorn 进行迭代。
通用求解器的示例
瓦瑟斯坦重心
瓦瑟斯坦重心是一个分布,它最小化与其他分布的瓦瑟斯坦距离 [16]。它对应于通过寻找一个分布 \(\mu\) 来最小化以下问题
在实际中,我们用有限数量的支持位置来建模一个分布:
其中 \(a\) 是单纯形上的直方图,\(\{x_i\}\) 是支撑的位置。我们可以清楚地看到,在这里优化 \(\mu\) 可以通过寻找最优权重 \(a\) 或最优支撑 \(\{x_i\}\) 来完成(同时优化两者也是一种选择)。我们在 POT 中提供解算器以估计在这两种情况下的离散 Wasserstein 重心。
具有固定支撑的重心
当对具有固定支持的重心进行优化时,优化问题可以表示为
其中 \(b_k\) 也是在简单形状中的权重。在非正则化情况下,上述问题是一个经典的线性规划。在这种情况下,我们提出了一个求解器 ot.lp.barycenter(),它依赖于通用的线性规划求解器。默认情况下,该函数使用 scipy.optimize.linprog,但可以通过更改参数 solver 来使用来自 cvxopt 的更高效的线性规划求解器。请注意,这个问题需要解决一个非常大的线性规划,在实际操作中可能会非常慢。
与OT问题类似,OT重心可以在正则化的情况下计算。当使用熵正则化时,可以通过基于Bregman投影的Sinkhorn算法的推广来解决该问题[3]。该算法在函数ot.bregman.barycenter中提供,也可以作为ot.barycenter获得。在这种情况下,该算法更适合处理大规模分布,并仅依赖于可以并行执行的矩阵乘法。
除了正则化带来的加速外,当支持具有可分离结构时,也可以大大加快Wasserstein重心的估计 [21]。以二维图像为例,可以用卷积算子替换Bregman投影中的矩阵向量乘法。我们提供了该算法的实现,函数为 ot.bregman.convolutional_barycenter2d。
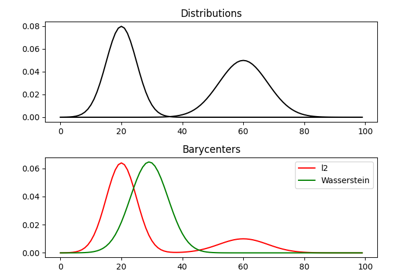
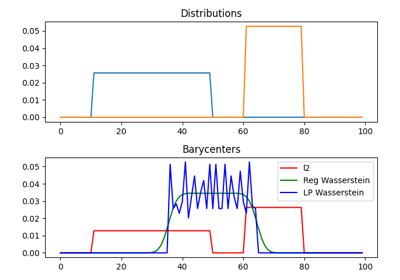
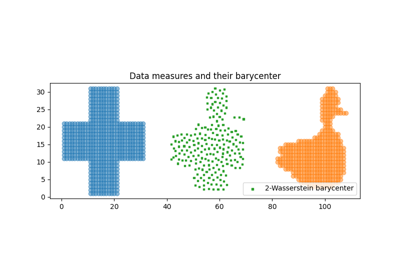
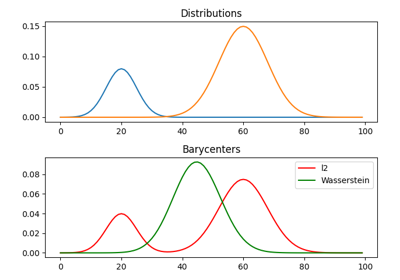
瓦瑟斯坦和正则化瓦瑟斯坦重心的例子
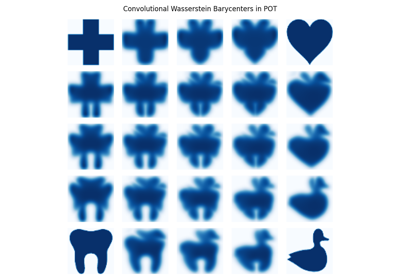
卷积重心的示例 (ot.bregman.convolutional_barycenter2d) 计算
自由支撑的重心
用自由支持但固定权重来估计Wasserstein重心相当于解决以下优化问题:
我们提供一个基于 [20] 的求解器在
ot.lp.free_support_barycenter。这个函数最小化问题并返回一个局部最优支持 \(\{x_i\}\) 用于均匀或给定的权重
\(a\)。
免费支持重心估计的示例
Monge映射和领域适应
由加斯帕尔·蒙日研究的原始运输问题是寻找一个映射函数,该函数在源分布和目标分布之间进行映射(或运输),但最小化运输损失。这种最优映射的存在性和唯一性在一般情况下仍然是一个未解的问题,但在光滑分布的情况下被布伦尼尔在他的同名定理中证明了。我们在ot.da中提供了几种用于光滑蒙日映射估计和从离散分布中进行领域适应的求解器。
蒙日映射估计
我们现在讨论在POT中实现的几种方法,以估计或近似来自有限分布的Monge映射。
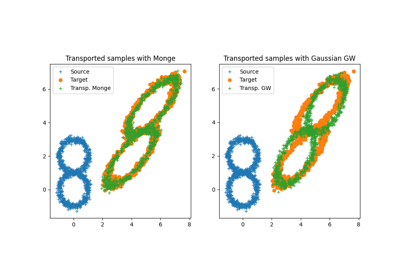
首先请注意,当源分布和目标分布被认为是高斯分布时,存在一个映射的闭合形式解,它是一个仿射函数 [14],形式为 \(T(x)=Ax+b\)。在这种情况下,我们提供函数 ot.gaussian.bures_wasserstein_mapping,该函数返回算子 \(A\) 和向量 \(b\)。请注意,如果样本数量过小,则有一个参数 reg,它为协方差矩阵的估计提供正则化。
为了更一般的映射估计,我们还提供了在 [6] 中提出的重心映射。它在 ot.da.EMDTransport 类中实现,以及在 ot.da 中的其他基于传输的类。关于这些类的讨论在下面会有更多内容,但它们遵循与 scikit-learn 类似的接口。最后,在 [8] 中提出的一种方法,估计一个连续映射以近似重心映射,其线性映射在 ot.da.joint_OT_mapping_linear 中提供,非线性映射在 ot.da.joint_OT_mapping_kernel 中提供。
领域适应类
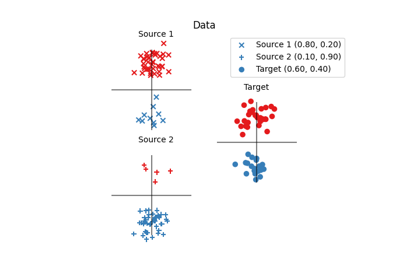
使用最优传输进行领域适应(OTDA)首次在 [5] 中提出,该文献还引入了组Lasso正则化。OTDA的主要思想是估计源分布和目标分布之间样本的映射,这允许将带标签的源样本传输到没有标签的目标分布上。
我们提供多个基于 ot.da.BaseTransport 的类,这些类提供多种 OT 和映射估计。 这些类的接口类似于 scikit-learn 中的分类器。 在初始化时,可以设置多个参数,例如正则化参数值。 然后需要使用函数 ot.da.BaseTransport.fit 估计映射。 最后,可以使用 ot.da.BaseTransport.transform 将样本从源映射到目标,并使用 ot.da.BaseTransport.inverse_transform 从目标映射到源。
这里是类 ot.da.EMDTransport 的一个例子:
ot_emd = ot.da.EMDTransport()
ot_emd.fit(Xs=Xs, Xt=Xt)
Xs_mapped = ot_emd.transform(Xs=Xs)
以下说明中提供了实现的列表。
注意
以下是继承自
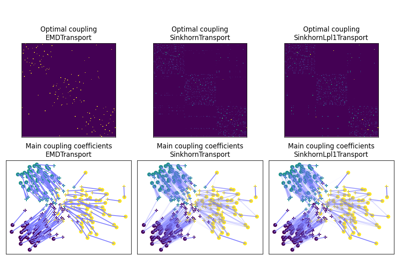
ot.da.BaseTransport的OT映射类列表
ot.da.EMDTransport: 基于EMD传输的重心映射ot.da.SinkhornTransport: 使用Sinkhorn传输的重心映射ot.da.SinkhornL1l2Transport: 使用Sinkhorn + 群体Lasso正则化的重心映射 [5]ot.da.SinkhornLpl1Transport: 使用Sinkhorn和非凸组Lasso正则化的重心映射 [5]ot.da.LinearTransport: 高斯之间的线性映射估计 [14]ot.da.MappingTransport: 非线性映射估计 [8]
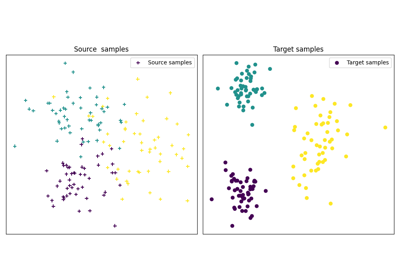
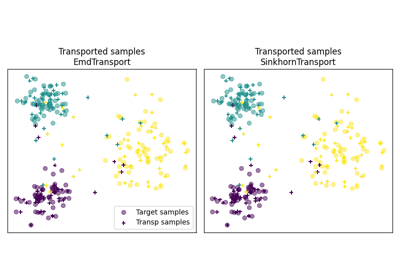
OTDA类的使用示例
不平衡和部分OT
不平衡最优传输
不平衡OT是熵正则化OT问题的一种放松形式,其中对边际的约束违反被添加到优化问题的目标中。两个不平衡直方图a和b之间的不平衡OT度量定义为[25] [10]:
其中 KL 是 Kullback-Leibler 散度。这个公式允许计算不具有相同质量的分布之间的近似映射。有趣的是,问题可以通过 Bregman 投影算法的推广来解决 [10]。我们为不平衡 OT 提供了一个求解器在 ot.unbalanced 中。计算最优运输方案或运输成本与平衡情况类似。Sinkhorn-Knopp 算法在 ot.sinkhorn_unbalanced 和 ot.sinkhorn_unbalanced2 中实现,分别返回 OT 矩阵和线性项的值。
注意
解决熵正则化UOT的主要功能是 ot.sinkhorn_unbalanced。该函数是一个封装器,参数 method 帮助您选择用于解决问题的实际算法:
method='sinkhorn'调用ot.unbalanced.sinkhorn_knopp_unbalanced广义的Sinkhorn算法 [25] [10]。method='sinkhorn_stabilized'调用ot.unbalanced.sinkhorn_stabilized_unbalanced该算法的对数稳定版本 [10]。
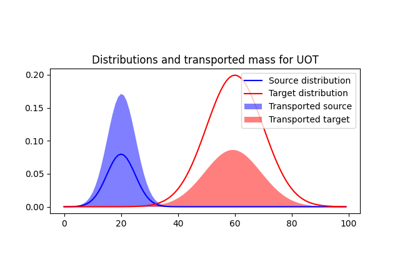
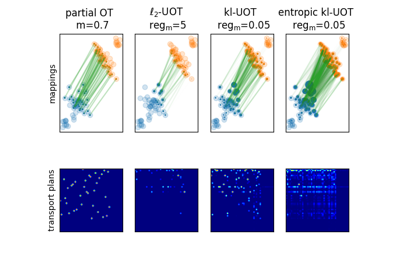
不平衡OT的示例
不平衡重心
与平衡分布类似,我们可以将具有不同质量的一组直方图的重心定义为Fréchet均值:
\[\min_{\mu} \quad \sum_{k} w_kW_u(\mu,\mu_k)\]
其中 \(W_u\) 是上述定义的非平衡Wasserstein度量。这个问题
也可以使用Sinkhorn算法的广义版本来解决,并且它在主函数 ot.barycenter_unbalanced 中实现。
注意
计算UOT重心的主要函数是 ot.barycenter_unbalanced。这个函数是一个包装器,参数 method 帮助您选择用于解决问题的实际算法:
method='sinkhorn'调用ot.unbalanced.barycenter_unbalanced_sinkhorn_unbalanced()广义的Sinkhorn算法 [10]。method='sinkhorn_stabilized'调用ot.unbalanced.barycenter_unbalanced_stabilized算法的对数稳定版本 [10]。
不平衡OT重心的示例
部分最优传输
部分最优运输是最优运输问题的一种变体,当仅需运输固定数量的质量 m 时。两个直方图 a 和 b 之间的部分最优运输度量定义为 [28]:
有趣的是,通过添加储量点,可以将这个问题转化为一个常规的OT问题,在这些储量点中,过剩的质量被发送[29]。我们提供了一个用于部分OT的求解器ot.partial。问题的精确解在ot.partial.partial_wasserstein和ot.partial.partial_wasserstein2中计算,分别返回OT矩阵和线性项的值。问题的熵解在ot.partial.entropic_partial_wasserstein中计算(见[3])。
问题的部分Gromov-Wasserstein公式化
在ot.partial.partial_gromov_wasserstein和ot.partial.entropic_partial_gromov_wasserstein中计算,当考虑问题的熵正则化时。
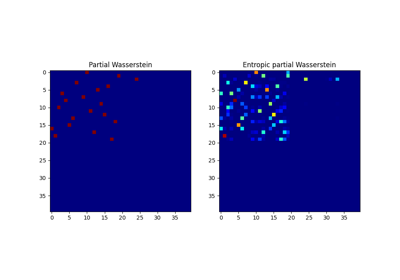
部分OT的示例
格罗莫夫-瓦瑟斯坦及其扩展
格罗莫夫-瓦瑟斯坦(GW)
Gromov Wasserstein (GW) 是 OT 的一种推广,适用于不在同一空间中的分布 [13]。在这种情况下,无法计算来自两个分布的样本之间的距离。[13] 提出了通过计算距离矩阵之间的传输来重新对齐度量空间。两个分布之间的 Gromov Wasserstein 对齐可以表示为最小化:
其中:\(C1\) 是源分布中样本之间的距离矩阵,\(C2\) 是目标中样本之间的距离矩阵,\(L(C1_{i,k},C2_{j,l})\) 是常用的相似度度量,通常选择为\(L(C1_{i,k},C2_{j,l})=\|C1_{i,k}-C2_{j,l}\|^2\)。上述优化问题是一个非凸二次规划,但我们提供了一个求解器,使用条件梯度在 ot.gromov.gromov_wasserstein 中找到局部最小值。还有一种提出的具有熵正则化的GW变体存在于[12],我们在 ot.gromov.entropic_gromov_wasserstein 中提供了他们算法的实现。
GW、正则化G和FGW的计算示例
格罗莫夫-瓦瑟斯坦重心
请注意,与Wasserstein距离类似,GW允许定义GW重心,可以表示为
其中 \(Ck\) 是分布中样本之间的距离矩阵 \(k\)。值得注意的是,重心被定义为对称正矩阵。我们提供了一个区块坐标优化程序在 ot.gromov.gromov_barycenters 和 ot.gromov.entropic_gromov_barycenters 中,分别用于非正则化和正则化的重心。
最后请注意,最近提出了一种Wasserstein和GW的融合,称为融合Gromov-Wasserstein(FGW)[24]。它可以计算那些仅部分在同一空间中的对象之间的相似性。因此,它可以用于测量标记图之间的相似性,并提供可计算的重心。FGW和FGW重心的实现提供在函数ot.gromov.fused_gromov_wasserstein和ot.gromov.fgw_barycenters中。
GW、正则化G和FGW重心的示例
其他应用
我们在下面讨论几个与OT相关的问题以及在OT和机器学习社区提出的工具。
瓦瑟斯坦判别分析
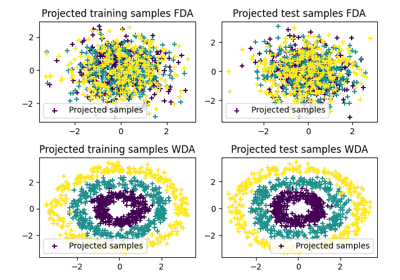
Wasserstein 判别分析 [11] 是 Fisher 线性判别分析 的一种推广,允许对不可线性分离的类进行区分。它的目的是找到一个线性投影器,以优化以下标准
其中 \(\#\) 是推前算子,\(OT_e\) 是熵OT损失,\(\mu_i\) 是来自类别 \(i\) 的样本分布。\(P\) 也被限制在斯蒂费尔流形中。WDA可以使用函数 ot.dr.wda 在POT中求解。它要求安装 pymanopt 和 autograd 以进行流形优化和自动微分。请注意,我们还在 ot.dr.fda 中提供了费舍尔判别估计器以便于比较。
警告
注意,由于对 pymanopt 和 autograd 的强依赖,ot.dr 并未默认导入。如果你想使用它,你必须特别导入它,使用 import ot.dr 。
WDA的使用示例
在CPU/GPU上使用多个后端解决OT
自版本0.8以来,POT提供了一个后端,允许独立于输入数组类型编写求解器。其思想是为用户提供一个无缝工作的包,当函数的输入为Pytorch张量时,返回的解实例将是Pytorch张量。
它是如何工作的
后端的目的是独立于输入数组的类型使用相同的函数。
例如,当执行以下代码时
# a and b are 1D histograms (sum to 1 and positive)
# M is the ground cost matrix
T = ot.emd(a, b, M) # exact linear program
w = ot.emd2(a, b, M) # Wasserstein computation
函数 ot.emd 和 ot.emd2 可以接受的输入类型为 numpy.array, torch.tensor 或 jax.numpy.array。函数的输出将与输入相同类型,并在相同设备上。当可能时,所有计算都在同一设备上进行,并且当可能时,输出将对函数的输入可微。
GPU加速
后端为大多数POT函数提供自动计算/兼容性,支持GPU。 请注意,所有依赖于C++精确OT求解器的求解器将需要在CPU上解决问题,这可能会导致一些内存复制开销,并且在所有其他计算在GPU上进行时可能远非最佳。它们仍然可以在GPU上的数组上工作,因为复制是自动完成的。
一些依赖于精确 C++ 求解器的函数包括:
兼容的后端列表
Numpy (所有函数和求解器)
Pytorch(所有输出相对于输入是可微分的)
Jax (某些函数是可微分的,某些需要一个包装器)
Tensorflow (所有输出相对于输入可微分)
Cupy(无微分,只有GPU)
该库会自动检测可用的后端。后端仅在必要时延迟实例化,以防止不必要的 GPU 内存分配。您还可以使用环境变量 POT_BACKEND_DISABLE_
兼容模块列表
这个列表会随着新版本的发布而变长,并且希望在POT完全与后端实现后消失。
常见问题
如何解决离散最优传输问题?
离散OT的求解器是函数
ot.emd,它返回 OT传输矩阵。如果您想解决一个正则化的OT,可以 使用ot.sinkhorn。这是一个简单的用例:
# a和b是1D直方图(和为1且为正) # M是基础费用矩阵 T = ot.emd(a, b, M) # 精确线性规划 T_reg = ot.sinkhorn(a, b, M, reg) # 熵正则化OT
可以在这个示例中看到更详细的例子: 二维经验分布之间的最优传输
pip安装POT失败,错误:ImportError: 没有名为Cython.Build的模块
如在README文件中简要讨论的,POT<0.8需要安装
numpy和cython才能构建。这个特殊情况尚未被pip处理, 因此您需要在安装POT之前先安装这两个库。请注意,当使用conda-forge时,这个问题不会发生,因为那里的软件包是预编译的。
有关更多细节,请查看问题 #59。
为什么Sinkhorn比EMD慢?
这可能与正则化项的选择有关。Sinkhorn的收敛速度直接依赖于这个项 [22]。当正则化变得非常小的时候,问题试图逼近精确的OT,这导致收敛慢以及数值问题。换句话说,对于较大的正则化,Sinkhorn的收敛速度非常快;而对于较小的正则化(当你需要一个接近真实OT的OT矩阵时),使用EMD求解器可能会更快。
还需注意,Sinkhorn的numpy实现可以根据系统配置使用并行计算,但通过使用GPU实现可以获得非常重要的速度提升,因为所有操作都是矩阵/向量乘法。