ot.utils

各种实用功能

函数

ot.utils.check_params(**kwargs)[源]

check_params: 检查是否缺少某些参数

ot.utils.check_random_state(seed)[源]

将 seed 转换为一个 np.random.RandomState 实例

Parameters:

seed (None | int | 实例 of RandomState) – 如果 seed 是 None, 返回 np.random 使用的 RandomState 单例。 如果 seed 是一个整数, 返回一个用 seed 初始化的新 RandomState 实例。 如果 seed 已经是一个 RandomState 实例, 返回它。 否则引发 ValueError。

ot.utils.clean_zeros(a, b, M)[源]

移除\(\mathbf{a}\)和\(\mathbf{b}\)中所有权重为零的组件

ot.utils.cost_normalization(C, norm=None, return_value=False, value=None)[源]

对损失矩阵应用归一化

Parameters:

  • C (ndarray, shape (n1, n2)) – 要归一化的成本矩阵。

  • norm (str) – 归一化类型，从‘median’，‘max’，‘log’，‘loglog’中选择。其他值将不进行归一化。

Returns:

C – 按照给定范数归一化的输入成本矩阵。

Return type:

ndarray, 形状 (n1, n2)

ot.utils.dist(x1, x2=None, metric='sqeuclidean', p=2, w=None)[源]

计算样本之间的距离在 \(\mathbf{x_1}\) 和 \(\mathbf{x_2}\)

注意

此函数与后端兼容，并且适用于所有兼容后端的数组。

Parameters:

  • x1 (类数组, 形状 (n1,d)) – 具有n1个样本，大小为d的矩阵

  • x2 (类数组, 形状 (n2,d), 可选) – 大小为d的n2个样本的矩阵 (如果为None，则\(\mathbf{x_2} = \mathbf{x_1}\))

  • metric (str | 可调用, 可选) – ‘sqeuclidean’ 或 ‘euclidean’ 在所有后端上。在 numpy 中，该函数还接受来自 scipy.spatial.distance.cdist 函数的：‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulczynski1’, ‘mahalanobis’, ‘matching’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘wminkowski’, ‘yule’.

  • p (float, 可选) – Minkowski 和加权 Minkowski 度量的 p-norm。默认值为 2。

  • w (类数组, 1阶) – 加权指标的权重。

Returns:

M – 使用给定度量计算的距离矩阵

Return type:

类似数组，形状 (n1, n2)

ot.utils.dist0(n, method='lin_square')[源]

计算OT问题的标准成本矩阵，大小为 (n, n)

Parameters:

  • n (int) – 成本矩阵的大小。

  • 方法 (str, 可选) –

    选择的损失矩阵类型：

    • ’lin_square’ : 在 0 和 n-1 之间的线性采样，二次损失

Returns:

M – 使用给定度量计算的距离矩阵。

Return type:

ndarray, 形状 (n1, n2)

使用 ot.utils.dist0 的示例

一维 Wasserstein 重心演示

1D Wasserstein 重心演示

去偏倚的Sinkhorn重心演示

去偏差的Sinkhorn重心演示

1D 沃瑟斯坦重心：精确线性规划与熵正则化

1D Wasserstein 重心：精确线性规划与熵正则化

不平衡分布的1D Wasserstein重心演示

不平衡分布的1D Wasserstein 重心演示
ot.utils.dots(*args)[源]

多个矩阵相乘的dots函数

ot.utils.euclidean_distances(X, Y, squared=False)[源]

考虑到\(\mathbf{X}\)（和\(\mathbf{Y} = \mathbf{X}\)）的行作为向量，计算每对向量之间的距离矩阵。

注意

此函数与后端兼容，并且适用于所有兼容后端的数组。

Parameters:

  • X (类似数组, 形状 (n_samples_1, n_features))

  • Y (类数组, 形状 (n_samples_2, n_features))

  • 平方 (布尔值, 可选) – 返回平方欧几里得距离。

Returns:

距离

Return type:

类似数组，形状（n_samples_1, n_samples_2）

ot.utils.get_coordinate_circle(x)[源]

对于 \(x\in S^1 \subset \mathbb{R}^2\)，返回坐标 依次 (在 [0,1[ 中)。

\[u = \frac{\pi + \mathrm{atan2}(-x_2,-x_1)}{2\pi}\]
Parameters:

x (ndarray, shape (n, 2)) – 环上的样本，带有环境坐标

Returns:

x_t – 坐标在 [0,1[ 上

Return type:

ndarray，形状 (n,)

示例

>>> u = np.array([[0.2,0.5,0.8]]) * (2 * np.pi)
>>> x1, y1 = np.cos(u), np.sin(u)
>>> x = np.concatenate([x1, y1]).T
>>> get_coordinate_circle(x)
array([0.2, 0.5, 0.8])
ot.utils.get_lowrank_lazytensor(Q, R, d=None, nx=None)[源]

获取一个低秩的 LazyTensor T=Q@R^T 或 T=Q@diag(d)@R^T

Parameters:

  • Q (ndarray, shape (n, r)) – 低秩张量的第一个因子

  • R (ndarray, shape (m, r)) – 低秩张量的第二个因子

  • d (ndarray, shape (r,), optional) – 低秩张量的对角线

  • nx (后端, 可选) – 用于减少的后端

Returns:

T – 低秩张量 T=Q@R^T 或 T=Q@diag(d)@R^T

Return type:

LazyTensor

ot.utils.get_parameter_pair(parameter)[源]

从给定参数中提取一对参数 用于不平衡的OT和COOT求解器 以处理边际正则化和熵正则化。

Parameters:

  • 参数 (浮点数 或 可索引对象)

  • nx (后端对象)

Returns:

  • param_1 (float)

  • param_2 (float)

ot.utils.is_all_finite(*args)[源]

逐个测试所有参数的有限性。

ot.utils.kernel(x1, x2, method='gaussian', sigma=1, **kwargs)[源]

计算核矩阵

ot.utils.label_normalization(y, start=0, nx=None)[源]

将标签变换为从给定值开始

Parameters:

  • y (类数组, 形状 (n, )) – 要归一化的标签向量。

  • start (int) – 在\(\mathbf{y}\)中所需的最小标签的值（默认为0）

  • nx (后端, 可选) – 用于执行计算的后端。如果省略，则后端默认为y的后端。

Returns:

y – 根据给定起始值规范化的标签输入向量。

Return type:

类似数组，形状 (n1, )

ot.utils.labels_to_masks(y, type_as=None, nx=None)[源]

将(n_samples,)标签向量转换为(n_samples, n_labels)掩码矩阵。

Parameters:

  • y (类似数组, 形状 (样本数量, )) – 标签的向量。

  • type_as (array_like) – 与预期输出相同类型的数组。

  • nx (后端, 可选) – 用于执行计算的后端。如果省略，则后端默认为y的后端。

Returns:

masks – 标签掩码的 (n_samples, n_labels) 矩阵。

Return type:

类似数组的对象，形状为 (n_samples, n_labels)

ot.utils.laplacian(x)[源]

计算拉普拉斯矩阵

ot.utils.list_to_array(*lst, nx=None)[源]

如果为numpy格式，请转换列表

ot.utils.parmap(f, X, nprocs='default')[源]

用于多进程的并行映射。该函数已被弃用，只执行常规映射。

ot.utils.proj_SDP(S, nx=None, vmin=0.0)[源]

将对称矩阵投影到特征值大于或等于vmin的对称矩阵空间。

Parameters:

  • S (array_like (n, d, d) 或 (d, d)) – 输入的对称矩阵或矩阵组。

  • nx (模块, 可选) – 要使用的数值后端模块。如果未提供，将从输入矩阵 S 中获取后端。

  • vmin (float, 可选) – 特征值的最小值。低于此值的特征值将被截断至 vmin。

  • 注意: (..) – 该函数与后端兼容，并将在数组上工作：来自所有兼容的后端。

Returns:

P – 预测的对称正定矩阵。

Return type:

ndarray (n, d, d) 或 (d, d)

使用 ot.utils.proj_SDP

GMM流程

GMM流程
ot.utils.proj_simplex(v, z=1)[源]

计算向量 \(\mathbf{v}\) 关于欧几里得距离在广义 (n-1)-单形上的最近点（正交投影），因此求解：

\[ \begin{align}\begin{aligned}\mathcal{P}(w) \in \mathop{\arg \min}_\gamma \| \gamma - \mathbf{v} \|_2\\s.t. \ \gamma^T \mathbf{1} = z\\ \gamma \geq 0\end{aligned}\end{align} \]

如果 \(\mathbf{v}\) 是一个二维数组，计算相对于轴 0 的所有投影

注意

此函数与后端兼容，并且适用于所有兼容后端的数组。

Parameters:

  • v ({类数组}, 形状 (n, d))

  • z (int, 可选) – 简单形的“大小”（每个向量的和为 z，默认为 1）

Returns:

h – 简单x上的投影数组

Return type:

ndarray, 形状 (n, d)

使用 ot.utils.proj_simplex 的示例

使用PyTorch进行Wasserstein去混合

使用PyTorch进行Wasserstein解混合

使用 PyTorch 的 Wasserstein 1D（流和重心）

使用PyTorch的Wasserstein 1D（流动和重心）

使用PyTorch优化Gromov-Wasserstein距离

使用PyTorch优化Gromov-Wasserstein距离

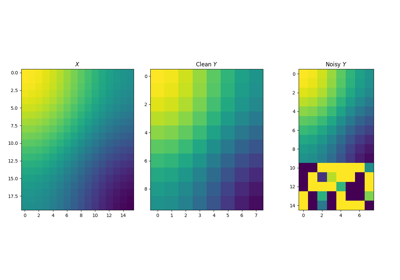
通过学习样本边际分布使用共同最优运输来检测异常值，并使用不平衡共同最优运输

通过学习样本的边际分布来检测异常值，使用CO-Optimal Transport和不平衡的Co-Optimal Transport

GMM流程

GMM流程
ot.utils.projection_sparse_simplex(V, max_nz, z=1, axis=None, nx=None)[源]

将 \(\mathbf{V}\) 投影到具有基数约束（非零元素的最大数量）的小 simplex 上，然后按 z 进行缩放。

\[\begin{split}P\left(\mathbf{V}, max_nz, z\right) = \mathop{\arg \min}_{\substack{\mathbf{y} >= 0 \\ \sum_i \mathbf{y}_i = z} \\ ||p||_0 \le \text{max_nz}} \quad \|\mathbf{y} - \mathbf{V}\|^2\end{split}\]
Parameters:

  • V (1维 或 2维 ndarray)

  • z (float 或 array) – 如果是数组，len(z) 必须与 \(\mathbf{V}\) 兼容

  • 轴 (无 或 整数) –

    • 轴=无: 通过 \(P(\mathbf{V}.\mathrm{ravel}(), max_nz, z)\) 投影 \(\mathbf{V}\)

    • 轴=1: 通过 \(P(\mathbf{V}_i, max_nz, z_i)\) 投影每个 \(\mathbf{V}_i\)

    • 轴=0: 通过 \(P(\mathbf{V}_{:, j}, max_nz, z_j)\) 投影每个 \(\mathbf{V}_{:, j}\)

Returns:

  • projection (ndarray, shape \(\mathbf{V}\).shape)

  • 参考文献 – 稀疏投影到简单形 Anastasios Kyrillidis, Stephen Becker, Volkan Cevher 和 Christoph Koch ICML 2013 https://arxiv.org/abs/1206.1529

ot.utils.reduce_lazytensor(a, func, axis=None, nx=None, batch_size=100)[源]

沿着一个轴使用函数 fun 和批次减少 LazyTensor。

当 axis=None 时，将 LazyTensor 减少为一个标量，作为沿 dim 进行批次处理的 fun 的总和。

警告

此函数适用于任意阶的张量，但可以在前两个轴（或全局）上进行缩减。同时，为了工作，它要求在要缩减的轴上（或如果axis=None则为轴0）有大小为batch_size的切片能够被计算并且适合内存。

Parameters:

  • a (LazyTensor) – 用于减少的LazyTensor

  • func (callable) – 应用到 LazyTensor 的函数

  • axis (int, 可选) – 用于减少LazyTensor的轴。如果为None，将LazyTensor减少为一个标量，作为沿着轴0的批次的fun的和。如果为0或1，将LazyTensor减少为一个向量/矩阵，作为沿着轴的批次的fun的和。

  • nx (后端, 可选) – 用于减少的后端

  • batch_size (int, 可选) – 用于减少的批量大小（默认=100）

Returns:

res – 减少的结果

Return type:

类似数组

ot.utils.tic()[源]

Matlab tic()函数的Python实现

ot.utils.toc(message='Elapsed time : {} s')[源]

Matlab toc() 函数的 Python 实现

ot.utils.toq()[源]

Python实现的Julia toc()函数

ot.utils.unif(n, type_as=None)[源]

返回长度为 n 的均匀直方图（单纯形）。

Parameters:

  • n (int) – 直方图中的箱子数量

  • type_as (array_like) – 与期望输出相同类型的数组 (numpy/pytorch/jax)

Returns:

h – 长度为 n 的直方图，使得 \(\forall i, \mathbf{h}_i = \frac{1}{n}\)

Return type:

类数组 (n,)

类

class ot.utils.BaseEstimator[源]

POT中大多数对象的基类

代码改编自sklearn BaseEstimator类

备注

所有估计器应在其 __init__ 中将所有可以在类级别设置的参数指定为显式关键字参数（不使用 *args 或 **kwargs）。

get_params(deep=True)[源]

获取此估计器的参数。

Parameters:

deep (bool, 可选) – 如果为真，将返回此估计器的参数和包含的子对象（它们也是估计器）。

Returns:

params – 参数名称映射到它们的值。

Return type:

字符串到任意类型的映射

set_params(**params)[源]

设置此估计器的参数。

该方法适用于简单估计器以及嵌套对象（例如管道）。后者具有形式为<component>__<parameter>的参数，因此可以更新嵌套对象的每个组件。

Return type:

自己

使用 ot.utils.BaseEstimator 的示例

用于领域适应的拉普拉斯正则化的OT

用于领域适应的拉普拉斯正则化的OT

图像颜色适应的OT

图像颜色适配的OT

领域适应的OT映射估计

用于领域适应的OT映射估计

用于图像颜色适应的映射估计的OT

用于图像颜色适应的OT与映射估计

OTDA 无监督与半监督设置

OTDA 无监督与半监督设置

线性OT映射估计

线性OT映射估计

用于领域适应的OT

用于领域适应的OT

用于经验分布域适应的OT

用于经验分布的领域适应的 OT

多源目标转移的OT

多源目标偏移的OT
class ot.utils.LazyTensor(shape, getitem, **kwargs)[源]

惰性张量是指未存储在内存中的张量。相反，它由一个函数定义，该函数根据切片动态计算其值。

Parameters:

  • shape (tuple) – 张量的形状

  • getitem (可调用) – 计算索引/切片和张量作为参数的值的函数

  • kwargs (dict) – 函数的命名参数，这些名称将作为LazyTensor对象的属性使用

示例

>>> import numpy as np
>>> v = np.arange(5)
>>> def getitem(i,j, v):
...     return v[i,None]+v[None,j]
>>> T = LazyTensor((5,5),getitem, v=v)
>>> T[1,2]
array([3])
>>> T[1,:]
array([[1, 2, 3, 4, 5]])
>>> T[:]
array([[0, 1, 2, 3, 4],
       [1, 2, 3, 4, 5],
       [2, 3, 4, 5, 6],
       [3, 4, 5, 6, 7],
       [4, 5, 6, 7, 8]])
class ot.utils.OTResult(potentials=None, value=None, value_linear=None, value_quad=None, plan=None, log=None, backend=None, sparse_plan=None, lazy_plan=None, status=None, batch_size=100)[源]

OT结果的基类。

Parameters:

  • potentials（数组类型的元组，形状为（n1，n2））– 对偶势， 即边际约束的拉格朗日乘数。 这对数组具有与输入权重“a”和“b”相同的形状、数值类型和属性。

  • 值 (浮点数, 类似数组) – 完整的运输成本，包括可能的正则化项和 Gromov Wasserstein 解决方案的二次项。

  • value_linear (float, array-like) – 运输成本的线性部分，即运输计划和成本之间的积。

  • value_quad (float, array-like) – Gromov-Wasserstein 解决方案的运输成本的二次部分。

  • plan （类似数组，形状（n1, n2））– 运输计划，编码为密集数组。

  • log (dict) – 包含关于求解器的潜在信息的字典。

  • 后端 (Backend) – 用于计算结果的后端。

  • sparse_plan (类数组, 形状 (n1, n2)) – 交通计划，编码为稀疏数组。

  • lazy_plan (LazyTensor) – 运输计划，以符号POT或KeOps LazyTensor编码。

  • status (int 或 str) – 求解器的状态。

  • batch_size (int) – 用于计算LazyTensor结果/边际的批量大小。

potentials

对偶潜力，即边际约束的拉格朗日乘子。 这一对数组具有与输入权重“a”和“b”相同的形状、数值类型和属性。

Type:

类似数组的元组，形状为 (n1, n2)

potential_a

第一个双重电位，与“源”测量“a”相关。

Type:

类数组，形状 (n1,)

potential_b

第二个双潜力，与“目标”度量“b”相关。

Type:

类似数组，形状 (n2,)

value

包含可能的正则化项和Gromov Wasserstein解的二次项的总运输成本。

Type:

float, 像数组的

value_linear

运输成本的线性部分，即运输计划与成本之间的乘积。

Type:

float, 像数组的

value_quad

Gromov-Wasserstein 解的运输成本的二次部分。

Type:

float, 像数组的

plan

运输计划，编码为稠密数组。

Type:

类似数组，形状 (n1, n2)

sparse_plan

运输计划，以稀疏数组编码。

Type:

类似数组，形状 (n1, n2)

lazy_plan

运输计划，编码为符号POT或KeOps LazyTensor。

Type:

LazyTensor

marginals

运输计划的边际：对于平衡的OT，应该非常接近“a”和“b”。

Type:

类数组的元组，形状为 (n1,), (n2,)

marginal_a

运输计划的“源”测量“a”的边际。

Type:

类数组，形状 (n1,)

marginal_b

“目标”测量“b”的运输计划的边际。

Type:

类似数组，形状 (n2,)

property a_to_b

第一个测量到第二个测量的位移向量。

property b_to_a

从第二次测量到第一次测量的位移向量。

property citation

该结果的适当引用，使用普通文本和BibTex格式。

property lazy_plan

运输计划，编码为符号的 KeOps LazyTensor。

property log

包含有关求解器的潜在信息的字典。

property marginal_a

运输计划的第一个边际，与“a”的形状相同。

property marginal_b

运输计划的第二个边际，与“b”的形状相同。

property marginals

对于平衡的OT，应该非常接近“a”和“b”。

Type:

运输计划的边际

property plan

运输计划，编码为稠密数组。

property potential_a

第一个双重电位，与“源”测量“a”相关。

property potential_b

第二个双潜力，与“目标”度量“b”相关。

property potentials

双重潜力，即边际约束的拉格朗日乘数。

这一对数组具有与输入权重“a”和“b”相同的形状、数值类型和属性。

property sparse_plan

运输计划，以稀疏数组编码。

property status

求解器的优化状态。

property value

包含可能的正则化项和Gromov Wasserstein解的二次项的总运输成本。

property value_linear

“最小”运输成本，即运输计划与成本之间的乘积。

property value_quad

Gromov-Wasserstein 解决方案的运输成本的二次部分。

class ot.utils.deprecated(extra='')[源]

装饰器，用于标记函数或类为不推荐使用。

来自 scikit-learn 包的已弃用类 https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/utils/deprecation.py 当调用该函数/实例化该类时发出警告，并 将警告添加到文档字符串中。 可选的额外参数将附加到弃用消息 和文档字符串中。

注意

要使用默认值的额外参数，请使用空括号：

>>> from ot.deprecation import deprecated  
>>> @deprecated()  
... def some_function(): pass
Parameters:

extra (str) – 将被添加到弃用消息中。

异常

UndefinedParameter

旨在引发异常，当调用未定义的参数时
class ot.utils.BaseEstimator[源]

POT中大多数对象的基类

代码改编自sklearn BaseEstimator类

备注

所有估计器应在其 __init__ 中将所有可以在类级别设置的参数指定为显式关键字参数（不使用 *args 或 **kwargs）。

get_params(deep=True)[源]

获取此估计器的参数。

Parameters:

deep (bool, 可选) – 如果为真，将返回此估计器的参数和包含的子对象（它们也是估计器）。

Returns:

params – 参数名称映射到它们的值。

Return type:

字符串到任意类型的映射

set_params(**params)[源]

设置此估计器的参数。

该方法适用于简单估计器以及嵌套对象（例如管道）。后者具有形式为<component>__<parameter>的参数，因此可以更新嵌套对象的每个组件。

Return type:

自己

class ot.utils.LazyTensor(shape, getitem, **kwargs)[源]

惰性张量是指未存储在内存中的张量。相反，它由一个函数定义，该函数根据切片动态计算其值。

Parameters:

  • shape (tuple) – 张量的形状

  • getitem (可调用) – 计算索引/切片和张量作为参数的值的函数

  • kwargs (dict) – 函数的命名参数，这些名称将作为LazyTensor对象的属性使用

示例

>>> import numpy as np
>>> v = np.arange(5)
>>> def getitem(i,j, v):
...     return v[i,None]+v[None,j]
>>> T = LazyTensor((5,5),getitem, v=v)
>>> T[1,2]
array([3])
>>> T[1,:]
array([[1, 2, 3, 4, 5]])
>>> T[:]
array([[0, 1, 2, 3, 4],
       [1, 2, 3, 4, 5],
       [2, 3, 4, 5, 6],
       [3, 4, 5, 6, 7],
       [4, 5, 6, 7, 8]])
class ot.utils.OTResult(potentials=None, value=None, value_linear=None, value_quad=None, plan=None, log=None, backend=None, sparse_plan=None, lazy_plan=None, status=None, batch_size=100)[源]

OT结果的基类。

Parameters:

  • potentials（数组类型的元组，形状为（n1，n2））– 对偶势， 即边际约束的拉格朗日乘数。 这对数组具有与输入权重“a”和“b”相同的形状、数值类型和属性。

  • 值 (浮点数, 类似数组) – 完整的运输成本，包括可能的正则化项和 Gromov Wasserstein 解决方案的二次项。

  • value_linear (float, array-like) – 运输成本的线性部分，即运输计划和成本之间的积。

  • value_quad (float, array-like) – Gromov-Wasserstein 解决方案的运输成本的二次部分。

  • plan （类似数组，形状（n1, n2））– 运输计划，编码为密集数组。

  • log (dict) – 包含关于求解器的潜在信息的字典。

  • 后端 (Backend) – 用于计算结果的后端。

  • sparse_plan (类数组, 形状 (n1, n2)) – 交通计划，编码为稀疏数组。

  • lazy_plan (LazyTensor) – 运输计划，以符号POT或KeOps LazyTensor编码。

  • status (int 或 str) – 求解器的状态。

  • batch_size (int) – 用于计算LazyTensor结果/边际的批量大小。

potentials

对偶潜力，即边际约束的拉格朗日乘子。 这一对数组具有与输入权重“a”和“b”相同的形状、数值类型和属性。

Type:

类似数组的元组，形状为 (n1, n2)

potential_a

第一个双重电位，与“源”测量“a”相关。

Type:

类数组，形状 (n1,)

potential_b

第二个双潜力，与“目标”度量“b”相关。

Type:

类似数组，形状 (n2,)

value

包含可能的正则化项和Gromov Wasserstein解的二次项的总运输成本。

Type:

float, 像数组的

value_linear

运输成本的线性部分，即运输计划与成本之间的乘积。

Type:

float, 像数组的

value_quad

Gromov-Wasserstein 解的运输成本的二次部分。

Type:

float, 像数组的

plan

运输计划，编码为稠密数组。

Type:

类似数组，形状 (n1, n2)

sparse_plan

运输计划，以稀疏数组编码。

Type:

类似数组，形状 (n1, n2)

lazy_plan

运输计划，编码为符号POT或KeOps LazyTensor。

Type:

LazyTensor

marginals

运输计划的边际：对于平衡的OT，应该非常接近“a”和“b”。

Type:

类数组的元组，形状为 (n1,), (n2,)

marginal_a

运输计划的“源”测量“a”的边际。

Type:

类数组，形状 (n1,)

marginal_b

“目标”测量“b”的运输计划的边际。

Type:

类似数组，形状 (n2,)

property a_to_b

第一个测量到第二个测量的位移向量。

property b_to_a

从第二次测量到第一次测量的位移向量。

property citation

该结果的适当引用，使用普通文本和BibTex格式。

property lazy_plan

运输计划，编码为符号的 KeOps LazyTensor。

property log

包含有关求解器的潜在信息的字典。

property marginal_a

运输计划的第一个边际，与“a”的形状相同。

property marginal_b

运输计划的第二个边际，与“b”的形状相同。

property marginals

对于平衡的OT，应该非常接近“a”和“b”。

Type:

运输计划的边际

property plan

运输计划，编码为稠密数组。

property potential_a

第一个双重电位，与“源”测量“a”相关。

property potential_b

第二个双潜力，与“目标”度量“b”相关。

property potentials

双重潜力，即边际约束的拉格朗日乘数。

这一对数组具有与输入权重“a”和“b”相同的形状、数值类型和属性。

property sparse_plan

运输计划，以稀疏数组编码。

property status

求解器的优化状态。

property value

包含可能的正则化项和Gromov Wasserstein解的二次项的总运输成本。

property value_linear

“最小”运输成本，即运输计划与成本之间的乘积。

property value_quad

Gromov-Wasserstein 解决方案的运输成本的二次部分。

exception ot.utils.UndefinedParameter[源]

旨在引发异常，当调用未定义的参数时

ot.utils.check_params(**kwargs)[源]

check_params: 检查是否缺少某些参数

ot.utils.check_random_state(seed)[源]

将 seed 转换为一个 np.random.RandomState 实例

Parameters:

seed (None | int | 实例 of RandomState) – 如果 seed 是 None, 返回 np.random 使用的 RandomState 单例。 如果 seed 是一个整数, 返回一个用 seed 初始化的新 RandomState 实例。 如果 seed 已经是一个 RandomState 实例, 返回它。 否则引发 ValueError。

ot.utils.clean_zeros(a, b, M)[源]

移除\(\mathbf{a}\)和\(\mathbf{b}\)中所有权重为零的组件

ot.utils.cost_normalization(C, norm=None, return_value=False, value=None)[源]

对损失矩阵应用归一化

Parameters:

  • C (ndarray, shape (n1, n2)) – 要归一化的成本矩阵。

  • norm (str) – 归一化类型，从‘median’，‘max’，‘log’，‘loglog’中选择。其他值将不进行归一化。

Returns:

C – 按照给定范数归一化的输入成本矩阵。

Return type:

ndarray, 形状 (n1, n2)

class ot.utils.deprecated(extra='')[源]

装饰器，用于标记函数或类为不推荐使用。

来自 scikit-learn 包的已弃用类 https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/utils/deprecation.py 当调用该函数/实例化该类时发出警告，并 将警告添加到文档字符串中。 可选的额外参数将附加到弃用消息 和文档字符串中。

注意

要使用默认值的额外参数，请使用空括号：

>>> from ot.deprecation import deprecated  
>>> @deprecated()  
... def some_function(): pass
Parameters:

extra (str) – 将被添加到弃用消息中。

ot.utils.dist(x1, x2=None, metric='sqeuclidean', p=2, w=None)[源]

计算样本之间的距离在 \(\mathbf{x_1}\) 和 \(\mathbf{x_2}\)

注意

此函数与后端兼容，并且适用于所有兼容后端的数组。

Parameters:

  • x1 (类数组, 形状 (n1,d)) – 具有n1个样本，大小为d的矩阵

  • x2 (类数组, 形状 (n2,d), 可选) – 大小为d的n2个样本的矩阵 (如果为None，则\(\mathbf{x_2} = \mathbf{x_1}\))

  • metric (str | 可调用, 可选) – ‘sqeuclidean’ 或 ‘euclidean’ 在所有后端上。在 numpy 中，该函数还接受来自 scipy.spatial.distance.cdist 函数的：‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulczynski1’, ‘mahalanobis’, ‘matching’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘wminkowski’, ‘yule’.

  • p (float, 可选) – Minkowski 和加权 Minkowski 度量的 p-norm。默认值为 2。

  • w (类数组, 1阶) – 加权指标的权重。

Returns:

M – 使用给定度量计算的距离矩阵

Return type:

类似数组，形状 (n1, n2)

ot.utils.dist0(n, method='lin_square')[源]

计算OT问题的标准成本矩阵，大小为 (n, n)

Parameters:

  • n (int) – 成本矩阵的大小。

  • 方法 (str, 可选) –

    选择的损失矩阵类型：

    • ’lin_square’ : 在 0 和 n-1 之间的线性采样，二次损失

Returns:

M – 使用给定度量计算的距离矩阵。

Return type:

ndarray, 形状 (n1, n2)

ot.utils.dots(*args)[源]

多个矩阵相乘的dots函数

ot.utils.euclidean_distances(X, Y, squared=False)[源]

考虑到\(\mathbf{X}\)（和\(\mathbf{Y} = \mathbf{X}\)）的行作为向量，计算每对向量之间的距离矩阵。

注意

此函数与后端兼容，并且适用于所有兼容后端的数组。

Parameters:

  • X (类似数组, 形状 (n_samples_1, n_features))

  • Y (类数组, 形状 (n_samples_2, n_features))

  • 平方 (布尔值, 可选) – 返回平方欧几里得距离。

Returns:

距离

Return type:

类似数组，形状（n_samples_1, n_samples_2）

ot.utils.get_coordinate_circle(x)[源]

对于 \(x\in S^1 \subset \mathbb{R}^2\)，返回坐标 依次 (在 [0,1[ 中)。

\[u = \frac{\pi + \mathrm{atan2}(-x_2,-x_1)}{2\pi}\]
Parameters:

x (ndarray, shape (n, 2)) – 环上的样本，带有环境坐标

Returns:

x_t – 坐标在 [0,1[ 上

Return type:

ndarray，形状 (n,)

示例

>>> u = np.array([[0.2,0.5,0.8]]) * (2 * np.pi)
>>> x1, y1 = np.cos(u), np.sin(u)
>>> x = np.concatenate([x1, y1]).T
>>> get_coordinate_circle(x)
array([0.2, 0.5, 0.8])
ot.utils.get_lowrank_lazytensor(Q, R, d=None, nx=None)[源]

获取一个低秩的 LazyTensor T=Q@R^T 或 T=Q@diag(d)@R^T

Parameters:

  • Q (ndarray, shape (n, r)) – 低秩张量的第一个因子

  • R (ndarray, shape (m, r)) – 低秩张量的第二个因子

  • d (ndarray, shape (r,), optional) – 低秩张量的对角线

  • nx (后端, 可选) – 用于减少的后端

Returns:

T – 低秩张量 T=Q@R^T 或 T=Q@diag(d)@R^T

Return type:

LazyTensor

ot.utils.get_parameter_pair(parameter)[源]

从给定参数中提取一对参数 用于不平衡的OT和COOT求解器 以处理边际正则化和熵正则化。

Parameters:

  • 参数 (浮点数 或 可索引对象)

  • nx (后端对象)

Returns:

  • param_1 (float)

  • param_2 (float)

ot.utils.is_all_finite(*args)[源]

逐个测试所有参数的有限性。

ot.utils.kernel(x1, x2, method='gaussian', sigma=1, **kwargs)[源]

计算核矩阵

ot.utils.label_normalization(y, start=0, nx=None)[源]

将标签变换为从给定值开始

Parameters:

  • y (类数组, 形状 (n, )) – 要归一化的标签向量。

  • start (int) – 在\(\mathbf{y}\)中所需的最小标签的值（默认为0）

  • nx (后端, 可选) – 用于执行计算的后端。如果省略，则后端默认为y的后端。

Returns:

y – 根据给定起始值规范化的标签输入向量。

Return type:

类似数组，形状 (n1, )

ot.utils.labels_to_masks(y, type_as=None, nx=None)[源]

将(n_samples,)标签向量转换为(n_samples, n_labels)掩码矩阵。

Parameters:

  • y (类似数组, 形状 (样本数量, )) – 标签的向量。

  • type_as (array_like) – 与预期输出相同类型的数组。

  • nx (后端, 可选) – 用于执行计算的后端。如果省略，则后端默认为y的后端。

Returns:

masks – 标签掩码的 (n_samples, n_labels) 矩阵。

Return type:

类似数组的对象，形状为 (n_samples, n_labels)

ot.utils.laplacian(x)[源]

计算拉普拉斯矩阵

ot.utils.list_to_array(*lst, nx=None)[源]

如果为numpy格式，请转换列表

ot.utils.parmap(f, X, nprocs='default')[源]

用于多进程的并行映射。该函数已被弃用，只执行常规映射。

ot.utils.proj_SDP(S, nx=None, vmin=0.0)[源]

将对称矩阵投影到特征值大于或等于vmin的对称矩阵空间。

Parameters:

  • S (array_like (n, d, d) 或 (d, d)) – 输入的对称矩阵或矩阵组。

  • nx (模块, 可选) – 要使用的数值后端模块。如果未提供，将从输入矩阵 S 中获取后端。

  • vmin (float, 可选) – 特征值的最小值。低于此值的特征值将被截断至 vmin。

  • 注意: (..) – 该函数与后端兼容，并将在数组上工作：来自所有兼容的后端。

Returns:

P – 预测的对称正定矩阵。

Return type:

ndarray (n, d, d) 或 (d, d)

ot.utils.proj_simplex(v, z=1)[源]

计算向量 \(\mathbf{v}\) 关于欧几里得距离在广义 (n-1)-单形上的最近点（正交投影），因此求解：

\[ \begin{align}\begin{aligned}\mathcal{P}(w) \in \mathop{\arg \min}_\gamma \| \gamma - \mathbf{v} \|_2\\s.t. \ \gamma^T \mathbf{1} = z\\ \gamma \geq 0\end{aligned}\end{align} \]

如果 \(\mathbf{v}\) 是一个二维数组，计算相对于轴 0 的所有投影

注意

此函数与后端兼容，并且适用于所有兼容后端的数组。

Parameters:

  • v ({类数组}, 形状 (n, d))

  • z (int, 可选) – 简单形的“大小”（每个向量的和为 z，默认为 1）

Returns:

h – 简单x上的投影数组

Return type:

ndarray, 形状 (n, d)

ot.utils.projection_sparse_simplex(V, max_nz, z=1, axis=None, nx=None)[源]

将 \(\mathbf{V}\) 投影到具有基数约束（非零元素的最大数量）的小 simplex 上，然后按 z 进行缩放。

\[\begin{split}P\left(\mathbf{V}, max_nz, z\right) = \mathop{\arg \min}_{\substack{\mathbf{y} >= 0 \\ \sum_i \mathbf{y}_i = z} \\ ||p||_0 \le \text{max_nz}} \quad \|\mathbf{y} - \mathbf{V}\|^2\end{split}\]
Parameters:

  • V (1维 或 2维 ndarray)

  • z (float 或 array) – 如果是数组，len(z) 必须与 \(\mathbf{V}\) 兼容

  • 轴 (无 或 整数) –

    • 轴=无: 通过 \(P(\mathbf{V}.\mathrm{ravel}(), max_nz, z)\) 投影 \(\mathbf{V}\)

    • 轴=1: 通过 \(P(\mathbf{V}_i, max_nz, z_i)\) 投影每个 \(\mathbf{V}_i\)

    • 轴=0: 通过 \(P(\mathbf{V}_{:, j}, max_nz, z_j)\) 投影每个 \(\mathbf{V}_{:, j}\)

Returns:

  • projection (ndarray, shape \(\mathbf{V}\).shape)

  • 参考文献 – 稀疏投影到简单形 Anastasios Kyrillidis, Stephen Becker, Volkan Cevher 和 Christoph Koch ICML 2013 https://arxiv.org/abs/1206.1529

ot.utils.reduce_lazytensor(a, func, axis=None, nx=None, batch_size=100)[源]

沿着一个轴使用函数 fun 和批次减少 LazyTensor。

当 axis=None 时，将 LazyTensor 减少为一个标量，作为沿 dim 进行批次处理的 fun 的总和。

警告

此函数适用于任意阶的张量，但可以在前两个轴（或全局）上进行缩减。同时，为了工作，它要求在要缩减的轴上（或如果axis=None则为轴0）有大小为batch_size的切片能够被计算并且适合内存。

Parameters:

  • a (LazyTensor) – 用于减少的LazyTensor

  • func (callable) – 应用到 LazyTensor 的函数

  • axis (int, 可选) – 用于减少LazyTensor的轴。如果为None，将LazyTensor减少为一个标量，作为沿着轴0的批次的fun的和。如果为0或1，将LazyTensor减少为一个向量/矩阵，作为沿着轴的批次的fun的和。

  • nx (后端, 可选) – 用于减少的后端

  • batch_size (int, 可选) – 用于减少的批量大小（默认=100）

Returns:

res – 减少的结果

Return type:

类似数组

ot.utils.tic()[源]

Matlab tic()函数的Python实现

ot.utils.toc(message='Elapsed time : {} s')[源]

Matlab toc() 函数的 Python 实现

ot.utils.toq()[源]

Python实现的Julia toc()函数

ot.utils.unif(n, type_as=None)[源]

返回长度为 n 的均匀直方图（单纯形）。

Parameters:

  • n (int) – 直方图中的箱子数量

  • type_as (array_like) – 与期望输出相同类型的数组 (numpy/pytorch/jax)

Returns:

h – 长度为 n 的直方图，使得 \(\forall i, \mathbf{h}_i = \frac{1}{n}\)

Return type:

类数组 (n,)