ot.dr

使用OT进行降维

警告

请注意，默认情况下该模块未在 ot 中导入。为了使用它，您需要显式导入 ot.dr

函数

ot.dr.dist(x1, x2)[源]

计算样本之间的平方欧几里得距离（自动求导）

ot.dr.ewca(X, U0=None, reg=1, k=2, method='BCD', sinkhorn_method='sinkhorn', stopThr=1e-06, maxiter=100, maxiter_sink=1000, maxiter_MM=10, verbose=0)[源]

熵瓦瑟斯坦成分分析 [52].

该函数解决以下优化问题：

\[\mathbf{U} = \mathop{\arg \min}_\mathbf{U} \quad W(\mathbf{X}, \mathbf{U}\mathbf{U}^T \mathbf{X})\]

其中 :

  • \(\mathbf{U}\) 是 Stiefel(p, d) 流形中的一个矩阵

  • \(W\) 是熵正则化的Wasserstein距离

  • \(\mathbf{X}\) 是样本

Parameters:

  • X (ndarray, shape (n, d)) – 来自测量的样本 \(\mu\)。

  • U0 (ndarray, shape (d, k), optional) – 投影的初始起点。

  • reg (float, 可选) – 正则化项 >0（熵正则化）。

  • k (int, 可选) – 子空间维度。

  • 方法 (str, 可选) – 选择‘BCD’或‘MM’（块坐标下降法或主化-最小化法）。当d很大时，优先选择MM。

  • sinkhorn_method (str) – 用于Sinkhorn求解器的方法，详见 ot.bregman.sinkhorn。

  • stopThr (float, 可选) – 错误的停止阈值 (>0)。

  • maxiter (int, 可选) – BCD/MM的最大迭代次数。

  • maxiter_sink (int, 可选) – Sinkhorn 求解器的最大迭代次数。

  • maxiter_MM (int, 可选) – MM的最大迭代次数（仅在method='MM'时使用）。

  • verbose (int, optional) – 在迭代过程中打印信息。

Returns:

  • pi (ndarray, shape (n, n)) – 给定参数的最优运输矩阵。

  • U (ndarray, shape (d, k)) – Stiefel 流形矩阵。

参考文献

使用 ot.dr.ewca 的示例

熵瓦瑟坦分量分析

熵瓦瑟斯坦分量分析
ot.dr.fda(X, y, p=2, reg=1e-16)[源]

费舍尔判别分析

Parameters:

  • X (ndarray, shape (n, d)) – 训练样本。

  • y (ndarray, shape (n,)) – 训练样本的标签。

  • p (int, 可选) – 维度减少的大小。

  • reg (float, 可选) – 正则化项 >0 （岭正则化）

Returns:

  • P (ndarray, shape (d, p)) – 给定参数的最优运输矩阵

  • proj (callable) – 包含均值中心化的投影函数

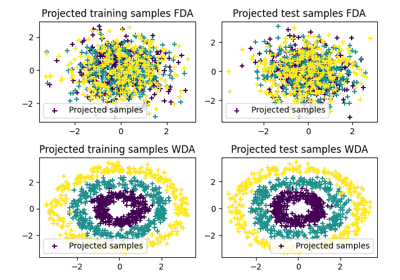
使用 ot.dr.fda 的示例

瓦瑟斯坦判别分析

瓦瑟斯坦判别分析
ot.dr.logsumexp(M, axis)[源]

与自动求导兼容的对数求和指数归约（无numpy实现）

ot.dr.projection_robust_wasserstein(X, Y, a, b, tau, U0=None, reg=0.1, k=2, stopThr=0.001, maxiter=100, verbose=0, random_state=None)[源]

投影鲁棒Wasserstein距离 [32]

该函数解决以下优化问题：

\[\max_{U \in St(d, k)} \ \min_{\pi \in \Pi(\mu,\nu)} \quad \sum_{i,j} \pi_{i,j} \|U^T(\mathbf{x}_i - \mathbf{y}_j)\|^2 - \mathrm{reg} \cdot H(\pi)\]

  • \(U\) 是Stiefel(d, k)流形中的线性投影算子

  • \(H(\pi)\) 是熵正则化器

  • \(\mathbf{x}_i\), \(\mathbf{y}_j\) 分别是测量值 \(\mu\) 和 \(\nu\) 的样本

Parameters:

  • X (ndarray, shape (n, d)) – 来自测量 \(\mu\) 的样本

  • Y (ndarray, shape (n, d)) – 来自测量 \(\nu\) 的样本

  • a (ndarray, shape (n, )) – 测量的权重 \(\mu\)

  • b (ndarray, shape (n, )) – 用于衡量 \(\nu\) 的权重

  • tau (float) – Riemannian梯度下降的步长

  • U0 (ndarray, shape (d, p)) – 投影的初始起点。

  • reg (float, optional) – 正则化项 >0 （熵正则化）

  • k (int) – 子空间维度

  • stopThr (float, 可选) – 错误的停止阈值 (>0)

  • verbose (int, optional) – 在迭代过程中打印信息。

  • random_state (int, RandomState 实例 或 None, 默认=None) – 确定当未给定 U0 时投影算子的初始值的随机数生成。

Returns:

  • pi (ndarray, shape (n, n)) – 给定参数的最优化运输矩阵

  • U (ndarray, shape (d, k)) – 投影操作符。

参考文献

ot.dr.sinkhorn(w1, w2, M, reg, k)[源]

固定迭代次数的Sinkhorn算法（自动求导）

ot.dr.sinkhorn_log(w1, w2, M, reg, k)[源]

具有固定迭代次数的对数域中的Sinkhorn算法（自动求导）

ot.dr.split_classes(X, y)[源]

按\(\mathbf{y}\)中的类别分割\(\mathbf{X}\)中的样本

ot.dr.wda(X, y, p=2, reg=1, k=10, solver=None, sinkhorn_method='sinkhorn', maxiter=100, verbose=0, P0=None, normalize=False)[源]

瓦瑟斯坦判别分析 [11]

该函数解决以下优化问题：

\[\mathbf{P} = \mathop{\arg \min}_\mathbf{P} \quad \frac{\sum\limits_i W(P \mathbf{X}^i, P \mathbf{X}^i)}{\sum\limits_{i, j \neq i} W(P \mathbf{X}^i, P \mathbf{X}^j)}\]

其中 :

  • \(P\) 是Stiefel(p, d)流形中的一个线性投影算子

  • \(W\) 是熵正则化的Wasserstein距离

  • \(\mathbf{X}^i\) 是对应于类别 i 的数据集中的样本

选择一个Sinkhorn求解器

默认情况下，当使用的正则化参数不是太小的时候，默认的 sinkhorn 求解器应该足够。如果您需要使用较小的正则化以获得稀疏的成本矩阵，您应该使用ot.dr.sinkhorn_log() 求解器，这可以避免数值错误，但在实际中可能会很慢。

Parameters:

  • X (ndarray, shape (n, d)) – 训练样本。

  • y (ndarray, shape (n,)) – 训练样本的标签。

  • p (int, 可选) – 维度减少的大小。

  • reg (float, optional) – 正则化项 >0 （熵正则化）

  • solver (无 | str, 可选) – 无用于最陡下降或‘TrustRegions’用于信任区域算法 否则应为一个 pymanopt.solvers

  • sinkhorn_method (str) – 用于Sinkhorn求解器的方法，可以是‘sinkhorn’或‘sinkhorn_log’

  • P0 (ndarray, shape (d, p)) – 投影的初始起点。

  • normalize (bool, 可选) – 通过 P0 上的平均距离归一化 Wasserstein 距离（默认值：False）

  • verbose (int, optional) – 在迭代过程中打印信息。

Returns:

  • P (ndarray, shape (d, p)) – 为给定参数的最优运输矩阵

  • proj (callable) – 包含均值中心化的投影函数。

参考文献

使用 ot.dr.wda 的示例

瓦瑟斯坦判别分析

瓦瑟斯坦判别分析
ot.dr.dist(x1, x2)[源]

计算样本之间的平方欧几里得距离（自动求导）

ot.dr.ewca(X, U0=None, reg=1, k=2, method='BCD', sinkhorn_method='sinkhorn', stopThr=1e-06, maxiter=100, maxiter_sink=1000, maxiter_MM=10, verbose=0)[源]

熵瓦瑟斯坦成分分析 [52].

该函数解决以下优化问题：

\[\mathbf{U} = \mathop{\arg \min}_\mathbf{U} \quad W(\mathbf{X}, \mathbf{U}\mathbf{U}^T \mathbf{X})\]

其中 :

  • \(\mathbf{U}\) 是 Stiefel(p, d) 流形中的一个矩阵

  • \(W\) 是熵正则化的Wasserstein距离

  • \(\mathbf{X}\) 是样本

Parameters:

  • X (ndarray, shape (n, d)) – 来自测量的样本 \(\mu\)。

  • U0 (ndarray, shape (d, k), optional) – 投影的初始起点。

  • reg (float, 可选) – 正则化项 >0（熵正则化）。

  • k (int, 可选) – 子空间维度。

  • 方法 (str, 可选) – 选择‘BCD’或‘MM’（块坐标下降法或主化-最小化法）。当d很大时，优先选择MM。

  • sinkhorn_method (str) – 用于Sinkhorn求解器的方法，详见 ot.bregman.sinkhorn。

  • stopThr (float, 可选) – 错误的停止阈值 (>0)。

  • maxiter (int, 可选) – BCD/MM的最大迭代次数。

  • maxiter_sink (int, 可选) – Sinkhorn 求解器的最大迭代次数。

  • maxiter_MM (int, 可选) – MM的最大迭代次数（仅在method='MM'时使用）。

  • verbose (int, optional) – 在迭代过程中打印信息。

Returns:

  • pi (ndarray, shape (n, n)) – 给定参数的最优运输矩阵。

  • U (ndarray, shape (d, k)) – Stiefel 流形矩阵。

参考文献

ot.dr.fda(X, y, p=2, reg=1e-16)[源]

费舍尔判别分析

Parameters:

  • X (ndarray, shape (n, d)) – 训练样本。

  • y (ndarray, shape (n,)) – 训练样本的标签。

  • p (int, 可选) – 维度减少的大小。

  • reg (float, 可选) – 正则化项 >0 （岭正则化）

Returns:

  • P (ndarray, shape (d, p)) – 给定参数的最优运输矩阵

  • proj (callable) – 包含均值中心化的投影函数

ot.dr.logsumexp(M, axis)[源]

与自动求导兼容的对数求和指数归约（无numpy实现）

ot.dr.projection_robust_wasserstein(X, Y, a, b, tau, U0=None, reg=0.1, k=2, stopThr=0.001, maxiter=100, verbose=0, random_state=None)[源]

投影鲁棒Wasserstein距离 [32]

该函数解决以下优化问题：

\[\max_{U \in St(d, k)} \ \min_{\pi \in \Pi(\mu,\nu)} \quad \sum_{i,j} \pi_{i,j} \|U^T(\mathbf{x}_i - \mathbf{y}_j)\|^2 - \mathrm{reg} \cdot H(\pi)\]

  • \(U\) 是Stiefel(d, k)流形中的线性投影算子

  • \(H(\pi)\) 是熵正则化器

  • \(\mathbf{x}_i\), \(\mathbf{y}_j\) 分别是测量值 \(\mu\) 和 \(\nu\) 的样本

Parameters:

  • X (ndarray, shape (n, d)) – 来自测量 \(\mu\) 的样本

  • Y (ndarray, shape (n, d)) – 来自测量 \(\nu\) 的样本

  • a (ndarray, shape (n, )) – 测量的权重 \(\mu\)

  • b (ndarray, shape (n, )) – 用于衡量 \(\nu\) 的权重

  • tau (float) – Riemannian梯度下降的步长

  • U0 (ndarray, shape (d, p)) – 投影的初始起点。

  • reg (float, optional) – 正则化项 >0 （熵正则化）

  • k (int) – 子空间维度

  • stopThr (float, 可选) – 错误的停止阈值 (>0)

  • verbose (int, optional) – 在迭代过程中打印信息。

  • random_state (int, RandomState 实例 或 None, 默认=None) – 确定当未给定 U0 时投影算子的初始值的随机数生成。

Returns:

  • pi (ndarray, shape (n, n)) – 给定参数的最优化运输矩阵

  • U (ndarray, shape (d, k)) – 投影操作符。

参考文献

ot.dr.sinkhorn(w1, w2, M, reg, k)[源]

固定迭代次数的Sinkhorn算法（自动求导）

ot.dr.sinkhorn_log(w1, w2, M, reg, k)[源]

具有固定迭代次数的对数域中的Sinkhorn算法（自动求导）

ot.dr.split_classes(X, y)[源]

按\(\mathbf{y}\)中的类别分割\(\mathbf{X}\)中的样本

ot.dr.wda(X, y, p=2, reg=1, k=10, solver=None, sinkhorn_method='sinkhorn', maxiter=100, verbose=0, P0=None, normalize=False)[源]

瓦瑟斯坦判别分析 [11]

该函数解决以下优化问题：

\[\mathbf{P} = \mathop{\arg \min}_\mathbf{P} \quad \frac{\sum\limits_i W(P \mathbf{X}^i, P \mathbf{X}^i)}{\sum\limits_{i, j \neq i} W(P \mathbf{X}^i, P \mathbf{X}^j)}\]

其中 :

  • \(P\) 是Stiefel(p, d)流形中的一个线性投影算子

  • \(W\) 是熵正则化的Wasserstein距离

  • \(\mathbf{X}^i\) 是对应于类别 i 的数据集中的样本

选择一个Sinkhorn求解器

默认情况下，当使用的正则化参数不是太小的时候，默认的 sinkhorn 求解器应该足够。如果您需要使用较小的正则化以获得稀疏的成本矩阵，您应该使用ot.dr.sinkhorn_log() 求解器，这可以避免数值错误，但在实际中可能会很慢。

Parameters:

  • X (ndarray, shape (n, d)) – 训练样本。

  • y (ndarray, shape (n,)) – 训练样本的标签。

  • p (int, 可选) – 维度减少的大小。

  • reg (float, optional) – 正则化项 >0 （熵正则化）

  • solver (无 | str, 可选) – 无用于最陡下降或‘TrustRegions’用于信任区域算法 否则应为一个 pymanopt.solvers

  • sinkhorn_method (str) – 用于Sinkhorn求解器的方法，可以是‘sinkhorn’或‘sinkhorn_log’

  • P0 (ndarray, shape (d, p)) – 投影的初始起点。

  • normalize (bool, 可选) – 通过 P0 上的平均距离归一化 Wasserstein 距离（默认值：False）

  • verbose (int, optional) – 在迭代过程中打印信息。

Returns:

  • P (ndarray, shape (d, p)) – 为给定参数的最优运输矩阵

  • proj (callable) – 包含均值中心化的投影函数。

参考文献