在两个时间序列中寻找保守模式#
AB-连接#
本教程改编自Matrix Profile I论文,并复制了图9和图10。
之前,我们介绍了一个概念叫做 time series motifs,它是在单个时间序列 \(T\) 中发现的保留模式,可以通过计算其 matrix profile 来发现,使用 STUMPY。这个使用单个时间序列计算矩阵分析的过程通常被称为“自连接”,因为时间序列 \(T\) 中的子序列仅与自身进行比较。然而,如果你有两个时间序列 \(T_{A}\) 和 \(T_{B}\),你想知道在 \(T_{A}\) 中是否有任何子序列也可以在 \(T_{B}\) 中找到,你该怎么做呢?通过扩展,涉及两个时间序列的模式发现过程通常被称为“AB-连接”,因为时间序列 \(T_{A}\) 中的所有子序列都与时间序列 \(T_{B}\) 中的所有子序列进行比较。
事实证明,“自连接”可以简单地推广到“AB连接”,生成的矩阵剖面为 \(T_{A}\) 中的每个子序列标注其在 \(T_{B}\) 中最近的子序列邻居,可以用来识别任何两个时间序列之间的相似(或唯一)子序列。此外,只要 \(T_{A}\) 和 \(T_{B}\) 的长度都大于或等于子序列长度 \(m\),则两个时间序列的长度不必相同。
在这个简短的教程中,我们将演示如何使用 STUMPY 在两个独立的时间序列中找到一个保守的模式。
开始使用#
让我们导入需要加载、分析和绘制数据的包。
%matplotlib inline
import stumpy
from stumpy import core
import pandas as pd
import numpy as np
from IPython.display import IFrame
import matplotlib.pyplot as plt
plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')
使用 STUMPY 查找音乐中的相似性#
在本教程中,我们将分析两首歌曲,“Under Pressure”由Queen和David Bowie演唱,以及“Ice Ice Baby”由Vanilla Ice演唱。对于那些不熟悉的人来说,在1990年,Vanilla Ice被指控未经原作者授权采样了“Under Pressure”的贝斯线,版权索赔后来庭外和解。请看这个简短的视频,看看你能否听出这两首歌之间的相似之处:
IFrame(width="560", height="315", src="https://www.youtube.com/embed/HAA__AW3I1M")
这两首歌确实有一些相似之处!但是,在我们继续之前,想象一下如果你是主持这个法庭案件的法官。为了使你深信不疑地确信存在不当行为,你需要看到什么分析结果?
正在加载音乐数据#
为了简化事情,我们将只使用已转换为单频率通道的音频,而不是每首歌的原始音乐音频(即,采样率为100Hz的第2个MFCC通道)。
queen_df = pd.read_csv("https://zenodo.org/record/4294912/files/queen.csv?download=1")
vanilla_ice_df = pd.read_csv("https://zenodo.org/record/4294912/files/vanilla_ice.csv?download=1")
print("Length of Queen dataset : " , queen_df.size)
print("Length of Vanilla ice dataset : " , vanilla_ice_df.size)
Length of Queen dataset : 24289
Length of Vanilla ice dataset : 23095
可视化音频频率#
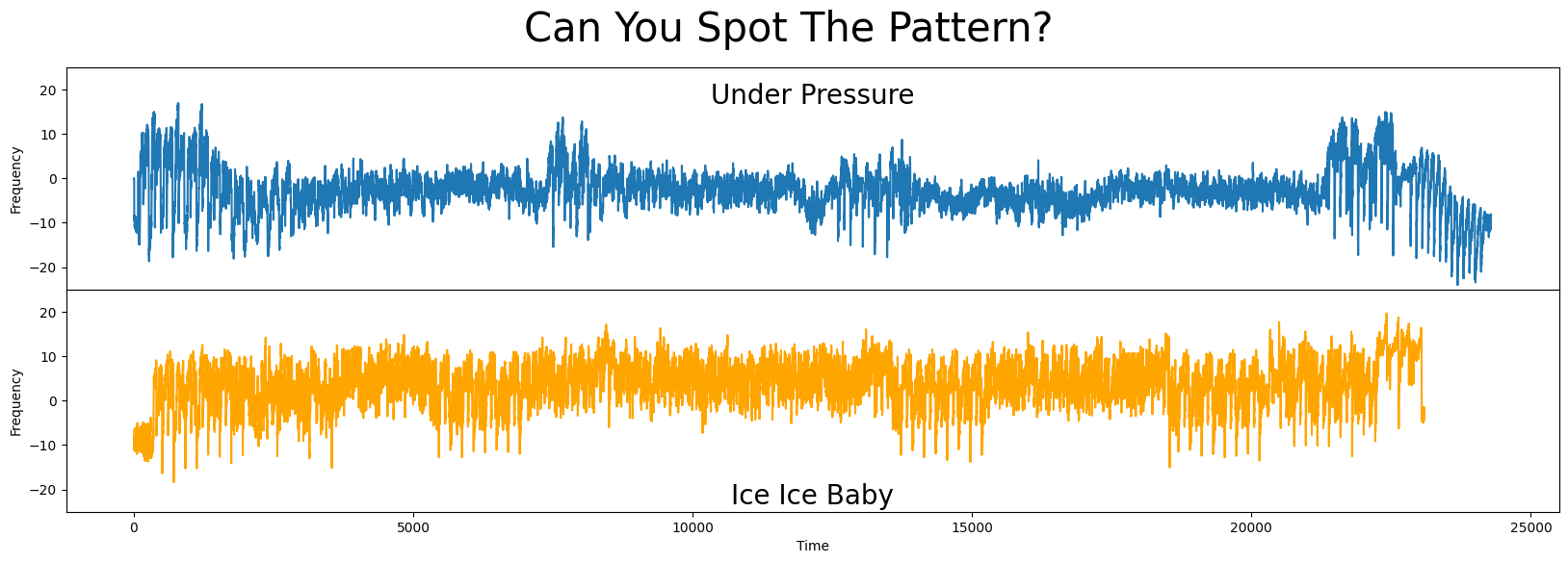
在之前的视频中,很明显这两首歌之间有很强的相似性。然而,即使有这个先前的知识,由于数据量庞大,确实很难发现相似之处(如下):
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Can You Spot The Pattern?', fontsize='30')
axs[0].set_title('Under Pressure', fontsize=20, y=0.8)
axs[1].set_title('Ice Ice Baby', fontsize=20, y=0)
axs[1].set_xlabel('Time')
axs[0].set_ylabel('Frequency')
axs[1].set_ylabel('Frequency')
ylim_lower = -25
ylim_upper = 25
axs[0].set_ylim(ylim_lower, ylim_upper)
axs[1].set_ylim(ylim_lower, ylim_upper)
axs[0].plot(queen_df['under_pressure'])
axs[1].plot(vanilla_ice_df['ice_ice_baby'], c='orange')
plt.show()
使用 STUMPY 执行 AB-Join#
幸运的是,使用 stumpy.stump 函数,我们可以通过执行 AB-连接快速计算矩阵轮廓,这将帮助我们轻松识别和定位这两首歌之间的相似子序列:
m = 500
queen_mp = stumpy.stump(T_A = queen_df['under_pressure'],
m = m,
T_B = vanilla_ice_df['ice_ice_baby'],
ignore_trivial = False)
上述内容中,我们通过指定两个时间序列 T_A = queen_df['under_pressure'] 和 T_B = vanilla_ice_df['ice_ice_baby'] 调用 stumpy.stump。遵循原始发表的工作,我们使用的子序列窗口长度为 m = 500,并且由于这不是自连接,我们设置 ignore_trivial = False。生成的矩阵轮廓 queen_mp 本质上作为对 T_A 的注释,因此对于 T_A 中的每个子序列,我们找到它在 T_B 中的最近子序列。
作为矩阵剖面数据结构的简要提醒,queen_mp 中的每一行对应于 T_A 中的每个子序列,queen_mp 中的第一列记录了 T_A 中每个子序列的矩阵剖面值(即到其在 T_B 中最近邻的距离),而 queen_mp 中的第二列记录了 T_B 中最近邻子序列的索引位置。
另一个附加说明是,AB-连接通常是不对称的。也就是说,与自连接不同,输入时间序列的顺序是重要的。因此,AB-连接将产生与BA-连接不同的矩阵轮廓(即,对于T_B中的每个子序列,我们找到其在T_A中最接近的子序列)。
可视化矩阵轮廓#
正如我们在过去所做的那样,我们现在可以查看从我们的AB连接计算出的矩阵剖面,queen_mp:
queen_motif_index = queen_mp[:, 0].argmin()
plt.xlabel('Subsequence')
plt.ylabel('Matrix Profile')
plt.scatter(queen_motif_index,
queen_mp[queen_motif_index, 0],
c='red',
s=100)
plt.plot(queen_mp[:,0])
plt.show()
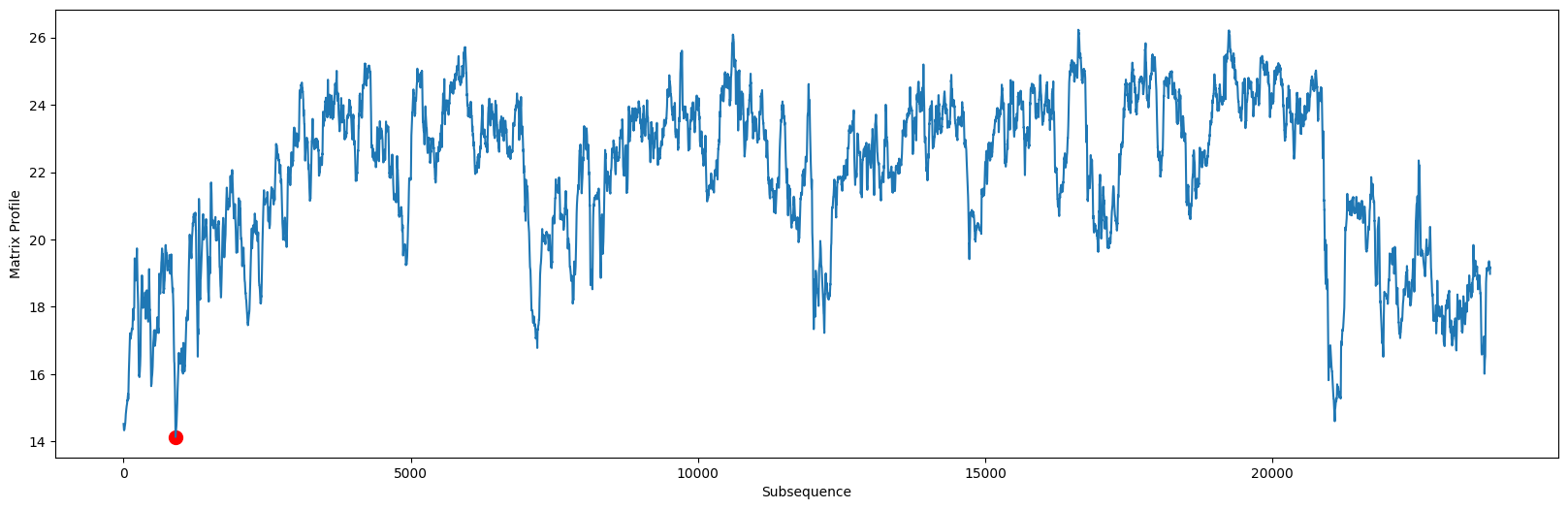
现在,为了发现全局模体(即,最保守的模式),queen_motif_index,我们只需识别queen_mp 矩阵轮廓中最低距离值的索引位置(见上面的红色圆圈)。
queen_motif_index = queen_mp[:, 0].argmin()
print(f'The motif is located at index {queen_motif_index} of "Under Pressure"')
The motif is located at index 904 of "Under Pressure"
事实上,它在“冰冰宝贝”中最近邻的索引位置存储在 queen_mp[queen_motif_index, 1]:
vanilla_ice_motif_index = queen_mp[queen_motif_index, 1]
print(f'The motif is located at index {vanilla_ice_motif_index} of "Ice Ice Baby"')
The motif is located at index 288 of "Ice Ice Baby"
在STUMPY版本1.12.0之后添加
可以通过 P_ 属性直接访问矩阵谱距离,通过 I_ 属性访问矩阵谱索引:
mp = stumpy.stump(T, m)
print(mp.P_, mp.I_) # print the matrix profile and the matrix profile indices
此外,左侧和右侧矩阵轮廓索引还可以通过 left_I_ 和 right_I_ 属性分别访问。
叠加最佳匹配的主题#
在识别出主题并从每首歌曲中获取索引位置后,让我们将这两个子序列叠加在一起,看看它们彼此之间有多相似:
queen_z_norm_motif = core.z_norm(queen_df.iloc[queen_motif_index : queen_motif_index + m].values)
vanilla_ice_z_norm_motif = core.z_norm(vanilla_ice_df.iloc[vanilla_ice_motif_index:vanilla_ice_motif_index+m].values)
plt.plot(queen_z_norm_motif, label='Under Pressure')
plt.plot(vanilla_ice_z_norm_motif, label='Ice Ice Baby')
plt.xlabel('Time')
plt.ylabel('Frequency')
plt.legend()
plt.show()
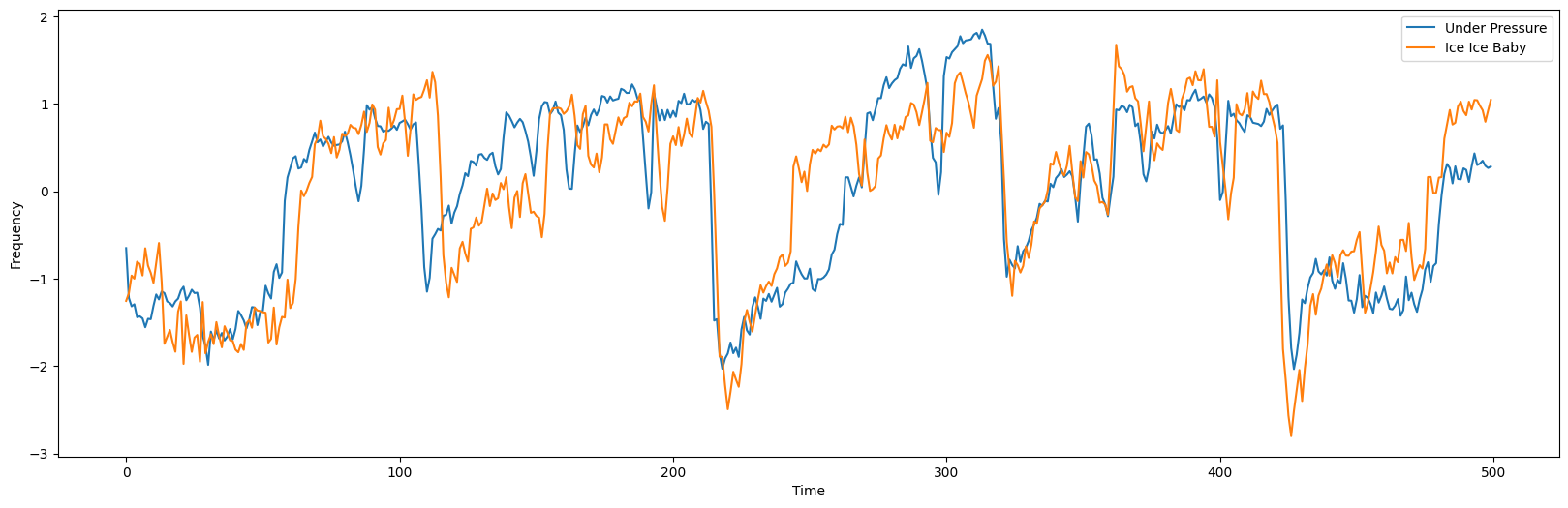
在绘图之前对你的子序列进行Z标准化
默认情况下,stumpy 在比较它们的矩阵轮廓距离之前,会对所有子序列进行z标准化(即,normalize=True)。因此,在我们可视化匹配的子序列之前,我们也必须先对它们进行z标准化。如果不这样做,子序列将以非标准化幅度进行绘制。子序列的z标准化可以通过使用 core.z_norm 辅助函数轻松完成:
from stumpy import core
core.z_norm(T[idx : idx + m])
然而,当计算矩阵轮廓距离时,如果normalize参数被设置为False,则应该省略此z标准化步骤。
哇,结果叠加显示了两个子序列之间非常强的相关性!你信服吗?
总结#
就这样!仅仅几行代码,你就学会了如何使用 STUMPY 计算两个时间序列的矩阵轮廓,并识别它们之间最保守的行为。虽然本教程主要集中在音频数据上,但还有许多其他应用,比如通过与已知的实验或历史故障数据集进行比较,检测传感器数据中的即将发生的机械问题,或者找到商品或股票价格中的匹配运动,仅举几例。
现在您可以导入此软件包并在自己的项目中使用。祝您编码愉快!
