矩阵剖面#

奠定基础#

在其核心，STUMPY库有效地计算一种称为 矩阵剖面，这是一个存储 z-标准化欧几里得距离 的向量，表示时间序列中任何子序列与其最近邻之间的距离。

要完全理解这意味着什么，让我们退一步，从一个简单的示例和一些基本定义开始：

长度为 n = 13 的时间序列#

time_series = [0, 1, 3, 2, 9, 1, 14, 15, 1, 2, 2, 10, 7]
n = len(time_series)

要分析这个长度为 n = 13 的时间序列，我们可以可视化数据或计算全局摘要统计（即均值、中位数、众数、最小值、最大值）。如果你有一个更长的时间序列，那么你可能甚至会想建立一个 ARIMA 模型、执行异常检测或尝试一个预测模型，但这些方法可能会很复杂，并且往往会有假阳性或没有可解释的见解。

Time Series Visualization

然而，如果我们应用奥卡姆剃刀，那么我们能采取的最简单和直观的方法来分析这个时间序列是什么？

要回答这个问题，我们先从我们的第一个定义开始：

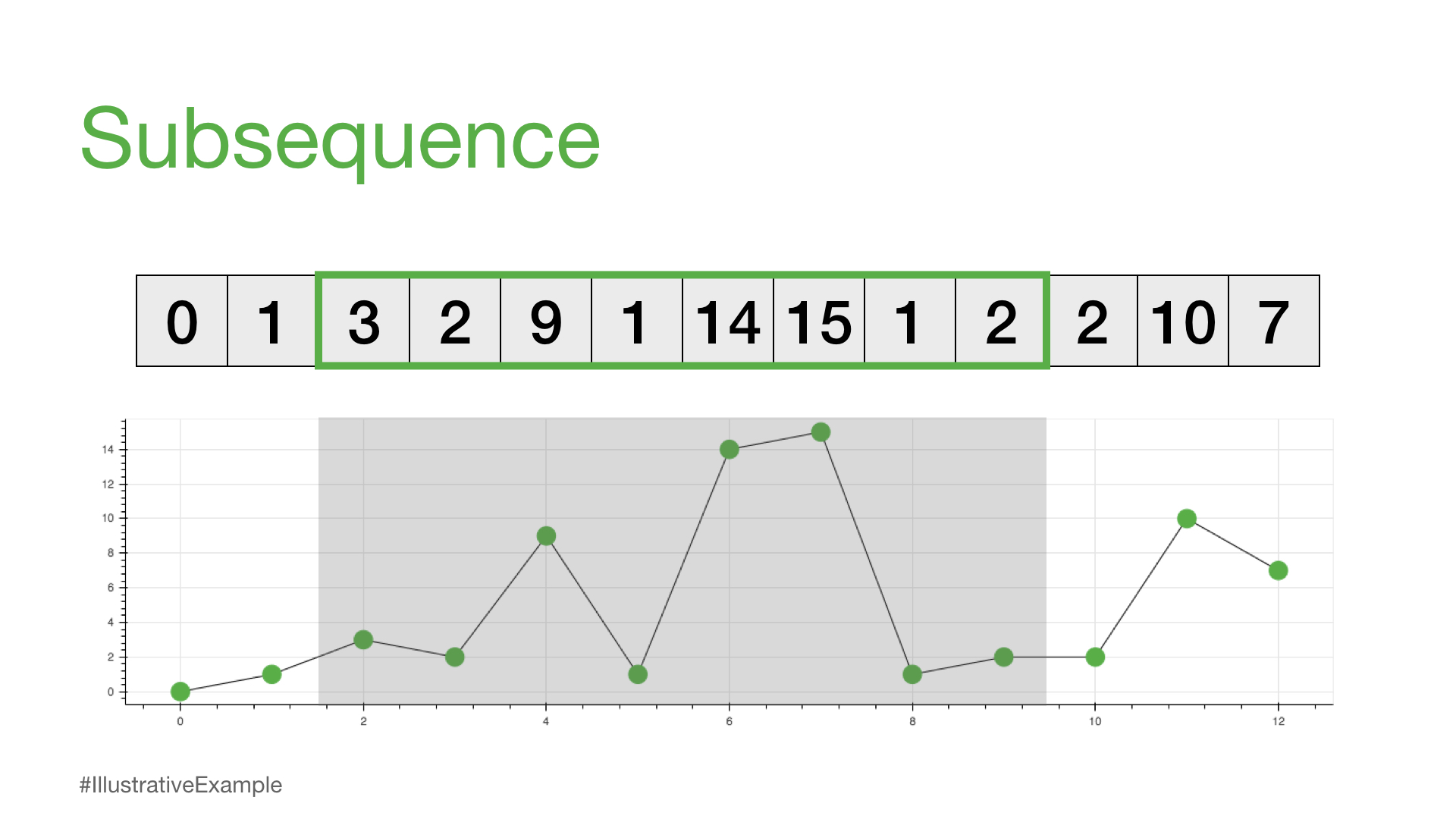
子序列 /ˈsəbsəkwəns/ 名词#

完整时间序列的一个部分或区域#

因此，以下内容都被认为是我们的 time_series 的子序列，因为它们都可以在上述时间序列中找到。

Subsequence 3 Subsequence 3 Subsequence 3

print(time_series[0:2])
print(time_series[4:7])
print(time_series[2:10])

[0, 1]
[9, 1, 14]
[3, 2, 9, 1, 14, 15, 1, 2]

我们可以看到，每个子序列可以有不同的序列长度，我们称之为 m。所以，例如，如果我们选择 m = 4，那么我们可以考虑如何比较任何两个相同长度的子序列。

m = 4
i = 0  # starting index for the first subsequence
j = 8  # starting index for the second subsequence

subseq_1 = time_series[i:i+m]
subseq_2 = time_series[j:j+m]

print(subseq_1, subseq_2)

[0, 1, 3, 2] [1, 2, 2, 10]

Subsequences

比较任何两个子序列的一种方法是计算所谓的欧几里得距离。

欧几里得距离 /yo͞oˈklidēən/ /ˈdistəns/ 名词#

两点之间的直线距离#

Euclidean Distance

import math

D = 0
for k in range(m):
    D += (time_series[i+k] - time_series[j+k])**2
print(f"The square root of {D} = {math.sqrt(D)}")

The square root of 67 = 8.18535277187245

距离剖面 - 成对欧几里得距离#

现在，我们可以更进一步，将一个子序列保持不变（参考子序列），以滑动窗口的方式改变第二个子序列，并计算每个窗口的欧几里得距离。得到的成对欧几里得距离向量也被称为距离轮廓。

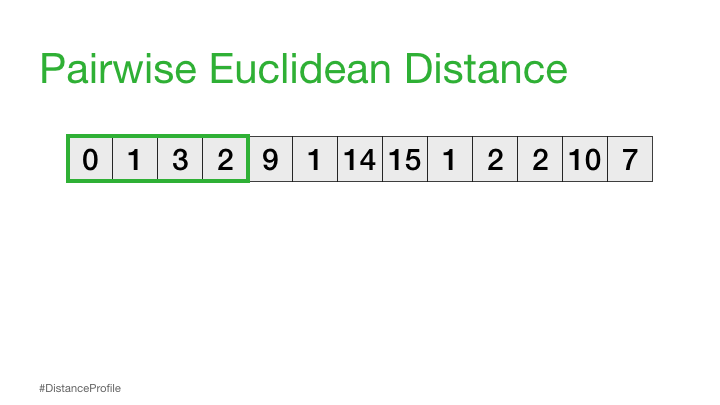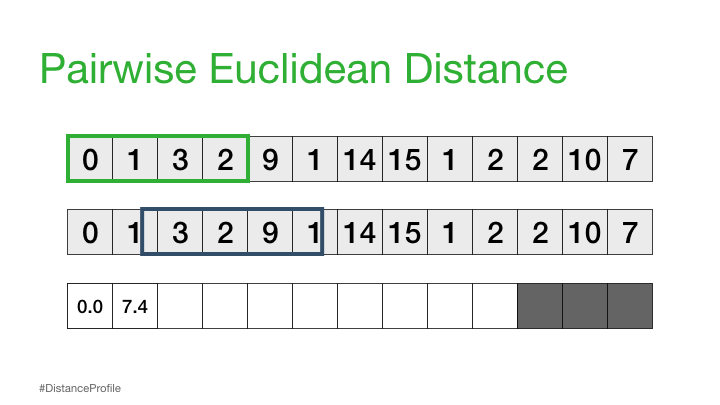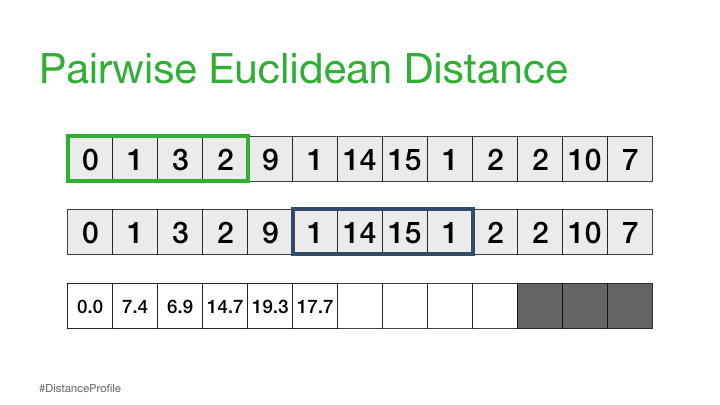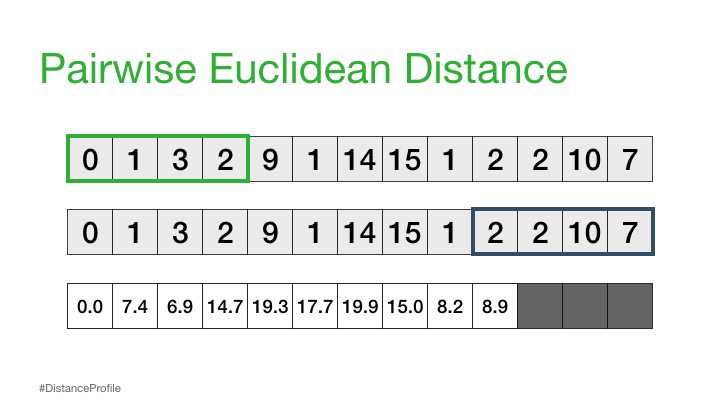
Pairwise Euclidean Distance

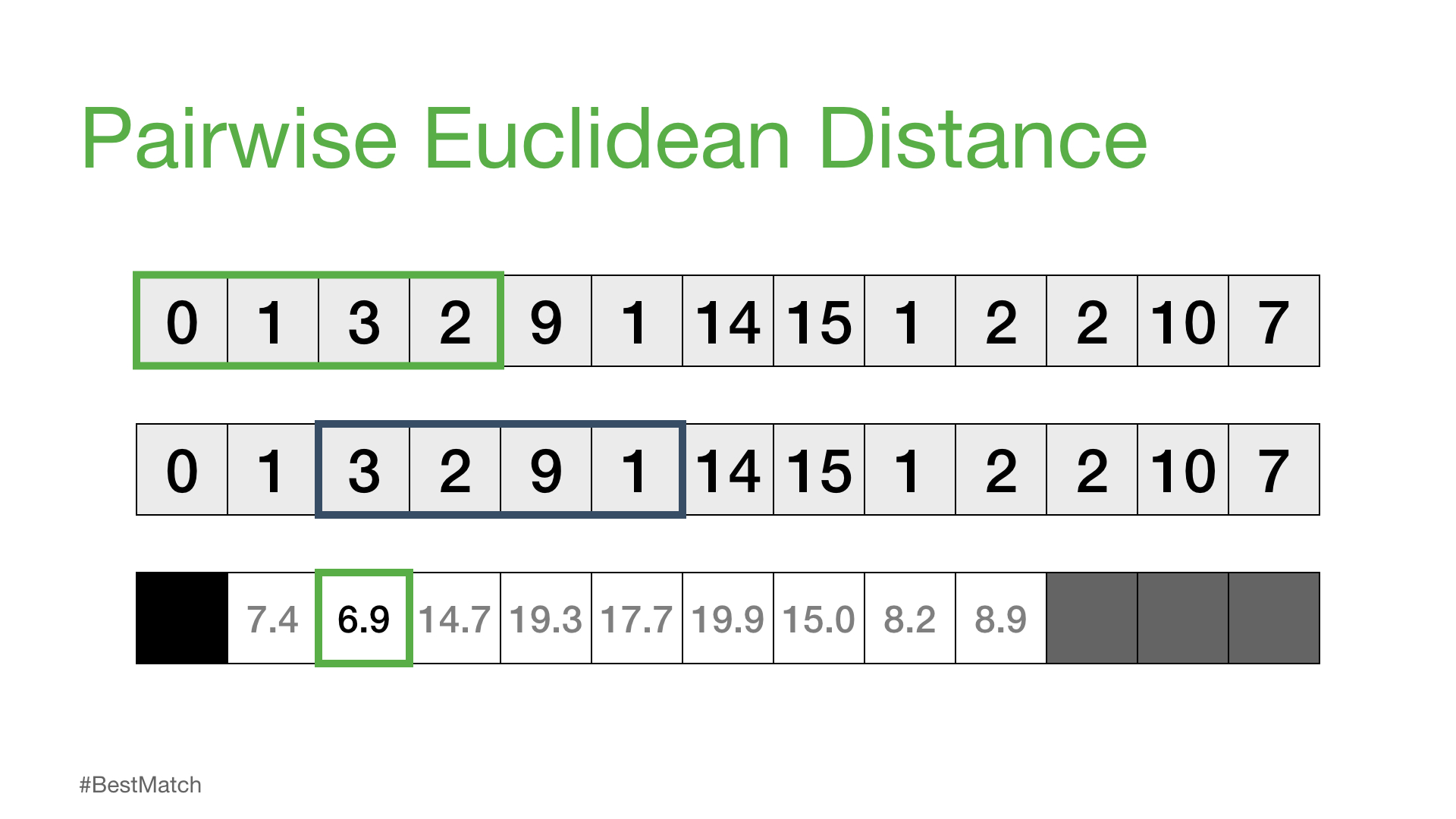
当然，并不是所有这些距离都是有用的。具体来说，自匹配（或平凡匹配）的距离并没有信息，因为当你将一个子序列与自身进行比较时，距离总是为零。因此，我们将忽略它，而是注意距离概况中下一个最小的距离，并将其作为我们最好的匹配：

Trivial Match

接下来，我们可以将参考子序列向右移动一个元素，并重复相同的滑动窗口过程，以计算每个新参考子序列的距离轮廓。

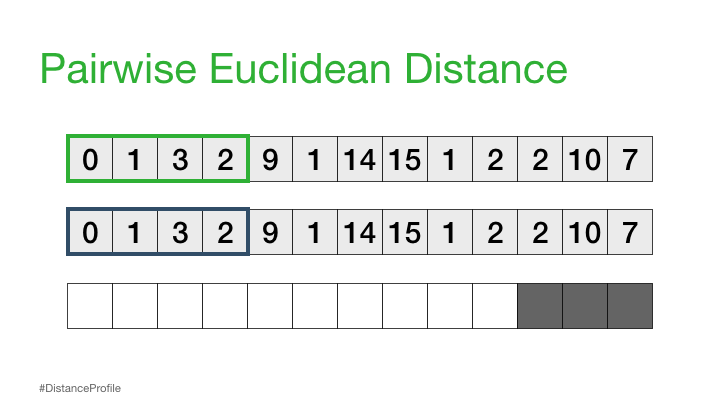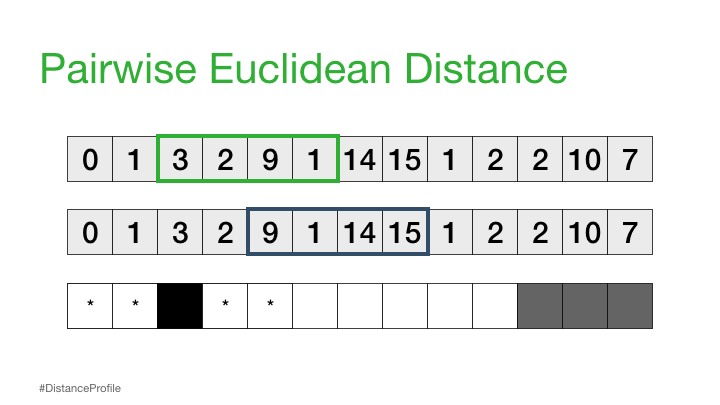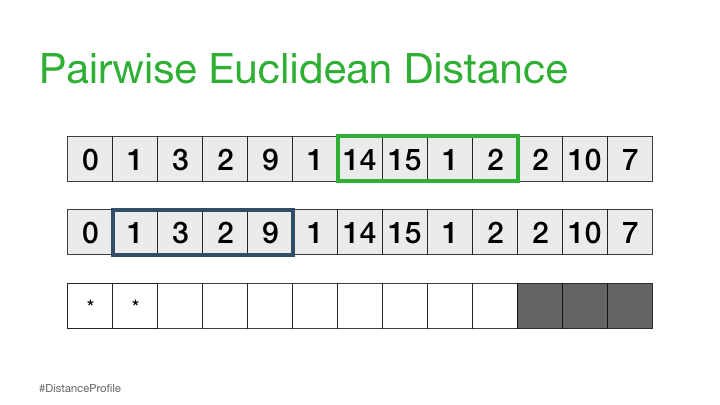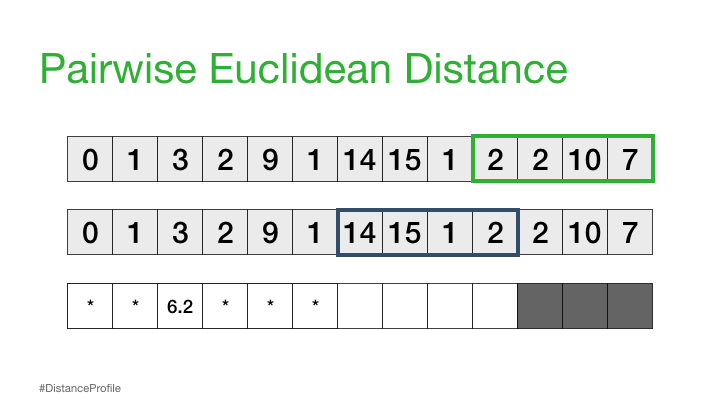
Distance Profiles

距离矩阵#

如果我们将为每个参考子序列计算的所有距离轮廓堆叠在一起，那么我们会得到一个称为 距离矩阵 的东西

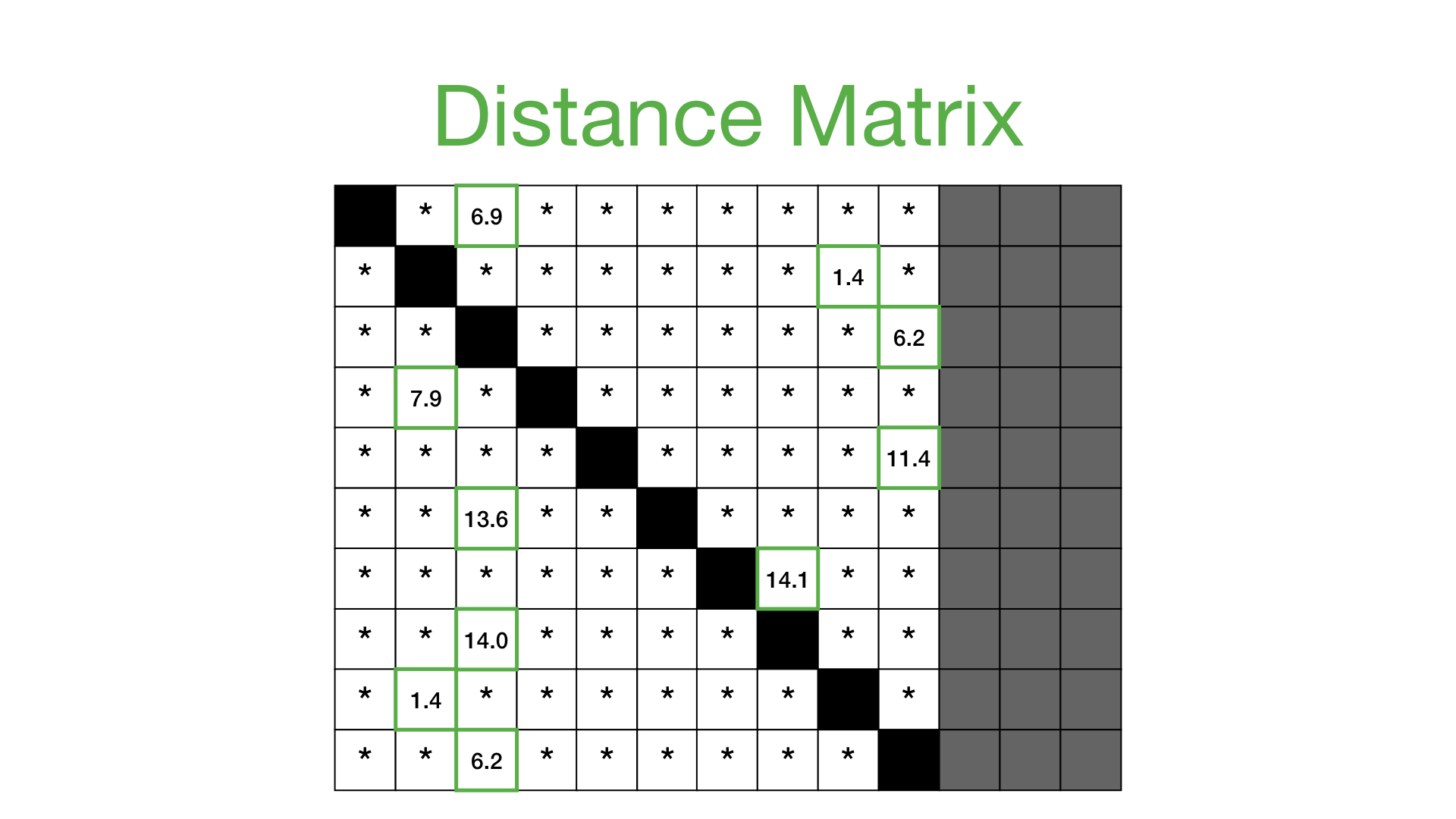
Distance Matrix

现在，我们可以通过仅查看每个子序列的最近邻来简化这个距离矩阵，这将引导我们进入下一个概念：

矩阵轮廓 /ˈmātriks/ /ˈprōˌfīl/ 名词#

一个向量，用于存储时间序列中任意子序列与其最近邻(z标准化)欧几里得距离#

实际上，这意味着矩阵剖面只关注存储每个距离剖面的最小非平凡距离，这显著降低了空间复杂度到 O(n)：

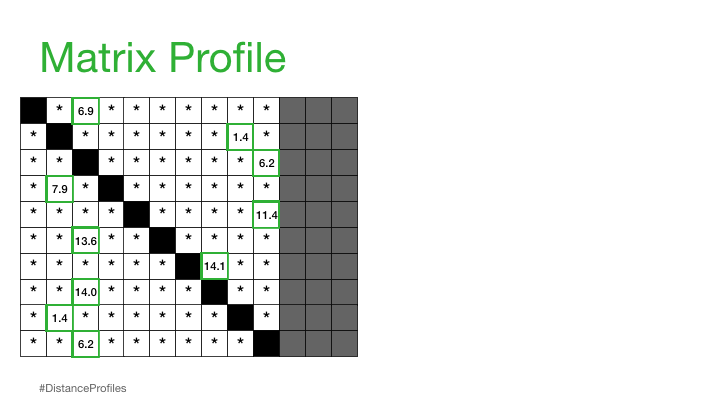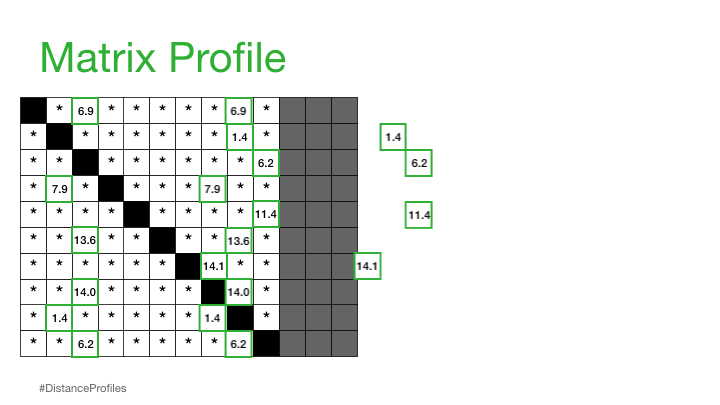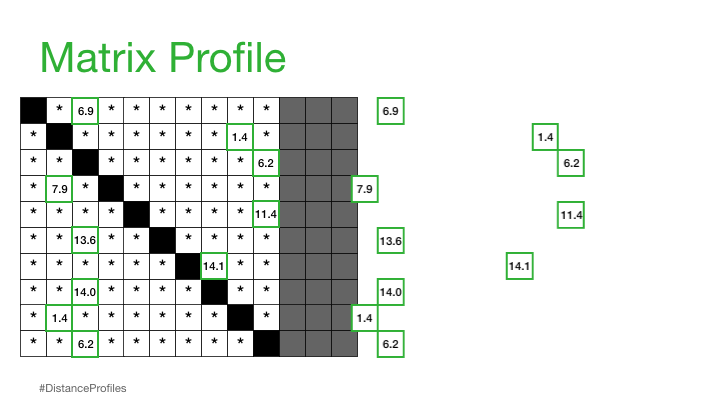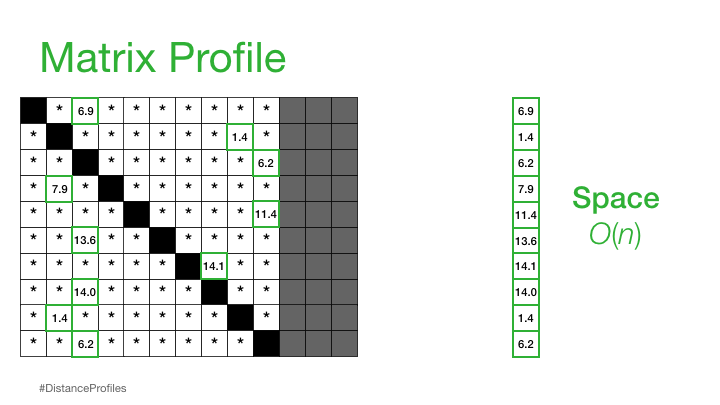
Matrix Profile

我们现在可以在我们原始时间序列下绘制这个矩阵配置文件。而且，事实证明，具有小矩阵配置文件值的参考子序列（即，它有一个明显“接近”的最近邻）可能表明一个可能的模式，而具有大矩阵配置文件值的参考子序列（即，它的最近邻显著“远离”）可能暗示存在异常。

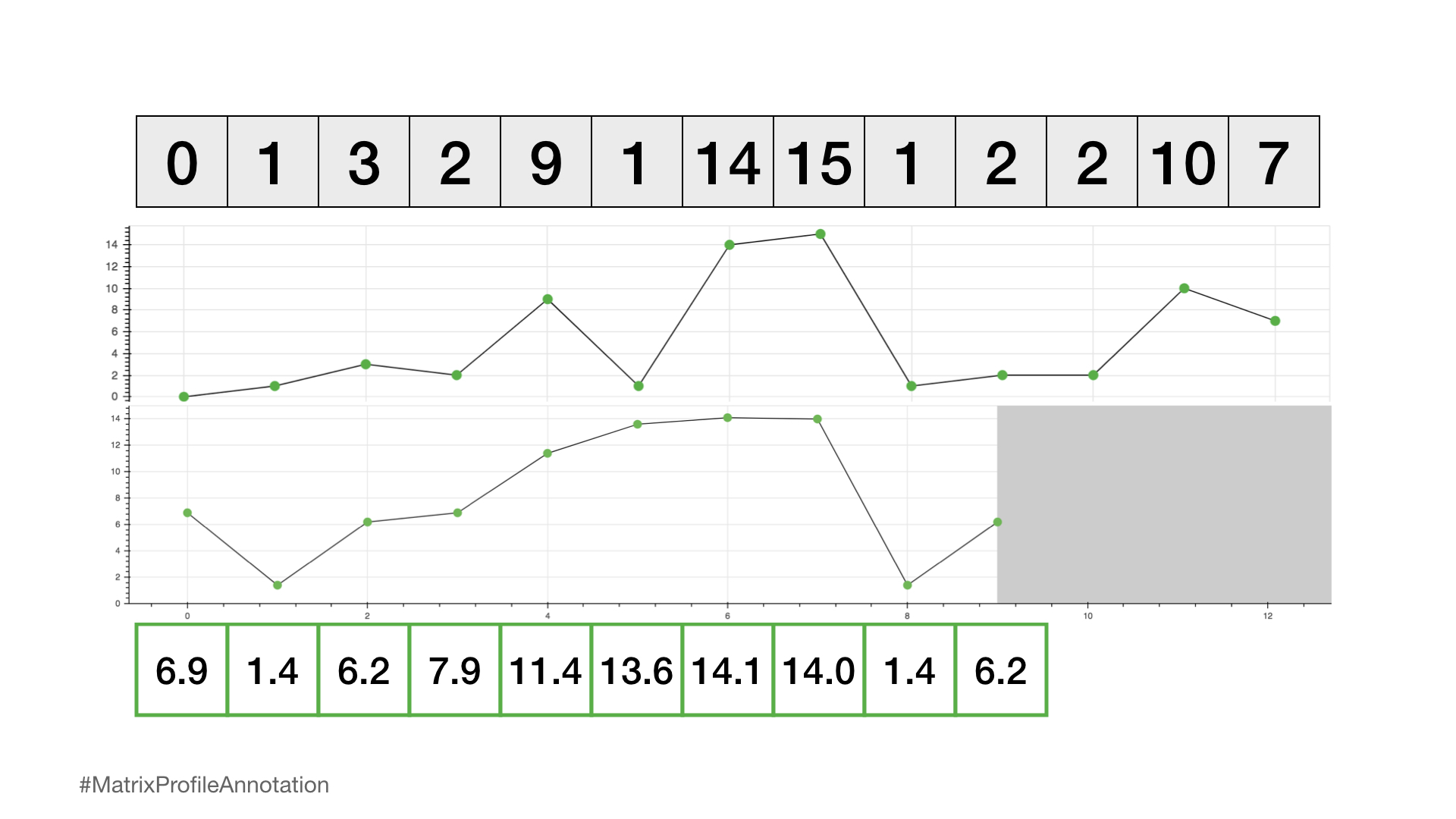
Time Series Matrix Profile

所以，仅仅通过计算和检查矩阵轮廓，就可以轻松地挑选出最优模式（全局最小值）和最稀有异常（全局最大值）。这只是计算矩阵轮廓后潜在可能性的一个小窗口！

真正的问题 - 粗暴搜索方法#

现在，这看起来可能相当简单，但我们需要考虑如何高效地计算完整的距离矩阵。让我们从暴力方法开始：

for i in range(n-m+1):
    for j in range(n-m+1):
        D = 0
        for k in range(m):
            D += (time_series[i+k] - time_series[j+k])**2
        D = math.sqrt(D)

乍一看，这可能看起来并不是太糟糕，但如果我们开始考虑计算复杂度和空间复杂度，那么我们就开始理解真正的问题。事实证明，对于较长的时间序列（即，n >> 10,000），计算复杂度为O(n2m)（如上面的代码中的三个for循环所证明的）而存储完整距离矩阵的空间复杂度为O(n2)。

为了更好地理解这一点，想象一下如果你有一个单一的传感器，在5年的时间里每分钟收集20次数据。这将导致：

n = 20 * 60 * 24 * 364 * 5  # 20 times/min x 60 mins/hour x 24 hours/day x 365 days/year x 5 years
print(f"There would be n = {n} data points")

There would be n = 52416000 data points

假设内循环中的每次计算需要0.0000001秒，那么这将需要：

time = 0.0000001 * (n * n - n)/2
print(f"It would take {time} seconds to compute")

It would take 137371850.1792 seconds to compute

这相当于1,598.7天（或4.4年）和11.1 PB的内存来计算！ 所以，显然使用我们简单粗暴的方法来计算距离矩阵是不可行的。相反，我们需要想办法通过有效生成矩阵剖面来降低这种计算复杂性，这就是STUMPY发挥作用的地方。

树桩#

在2016年秋季，加州大学河滨分校和新墨西哥大学的研究人员发表了一组优美的背靠背论文，描述了一种称为STOMP的精确方法，用于计算任何时间序列的矩阵轮廓，其计算复杂度为O(n2)！他们还进一步利用GPU进行了演示，并称这种更快的方法为GPU-STOMP。

考虑到学术界、数据科学家和开发者，我们基于已发表的研究，开发并开源了STUMPY，这是一款强大且可扩展的库，可以高效地计算矩阵剖面。此外，得益于其他开源软件，如 Numba 和 Dask，我们的实现具有高度的并行性（适用于具有多个CPU的单台服务器，或者多台GPU），以及高度的分布性（在多台服务器上使用多个CPU）。我们在多达256个CPU核心（分布在32台服务器上）或16个NVIDIA GPU设备（在同一DGX-2服务器上）上测试了STUMPY，并达到了与已发表的GPU-STOMP工作相似的 performance。

结论#

根据原作者的说法，“这些是过去二十年中时间序列数据挖掘的最佳想法”，并且“考虑到矩阵剖面， 大多数时间序列数据挖掘问题在几行代码中很容易解决”。

根据我们的经验，这绝对是真的，我们很高兴能与您分享STUMPY！请与我们联系，让我们知道STUMPY如何使您的时间序列分析工作得以实现，我们很想听听您的意见！

附加说明#

为了完整起见，我们将为那些希望将自己的矩阵轮廓实现与STUMPY进行比较的人提供更多的评论。然而，由于原始论文中省略了许多细节，我们强烈建议您使用STUMPY。

在我们上述的解释中，我们仅排除了简单匹配的考虑。然而，这是不够的，因为附近的子序列（即，i ± 1）可能非常相似，我们需要将此扩展到相对于对角线简单匹配的更大的“排除区域”。在这里，我们可以可视化不同的排除区域的样子：

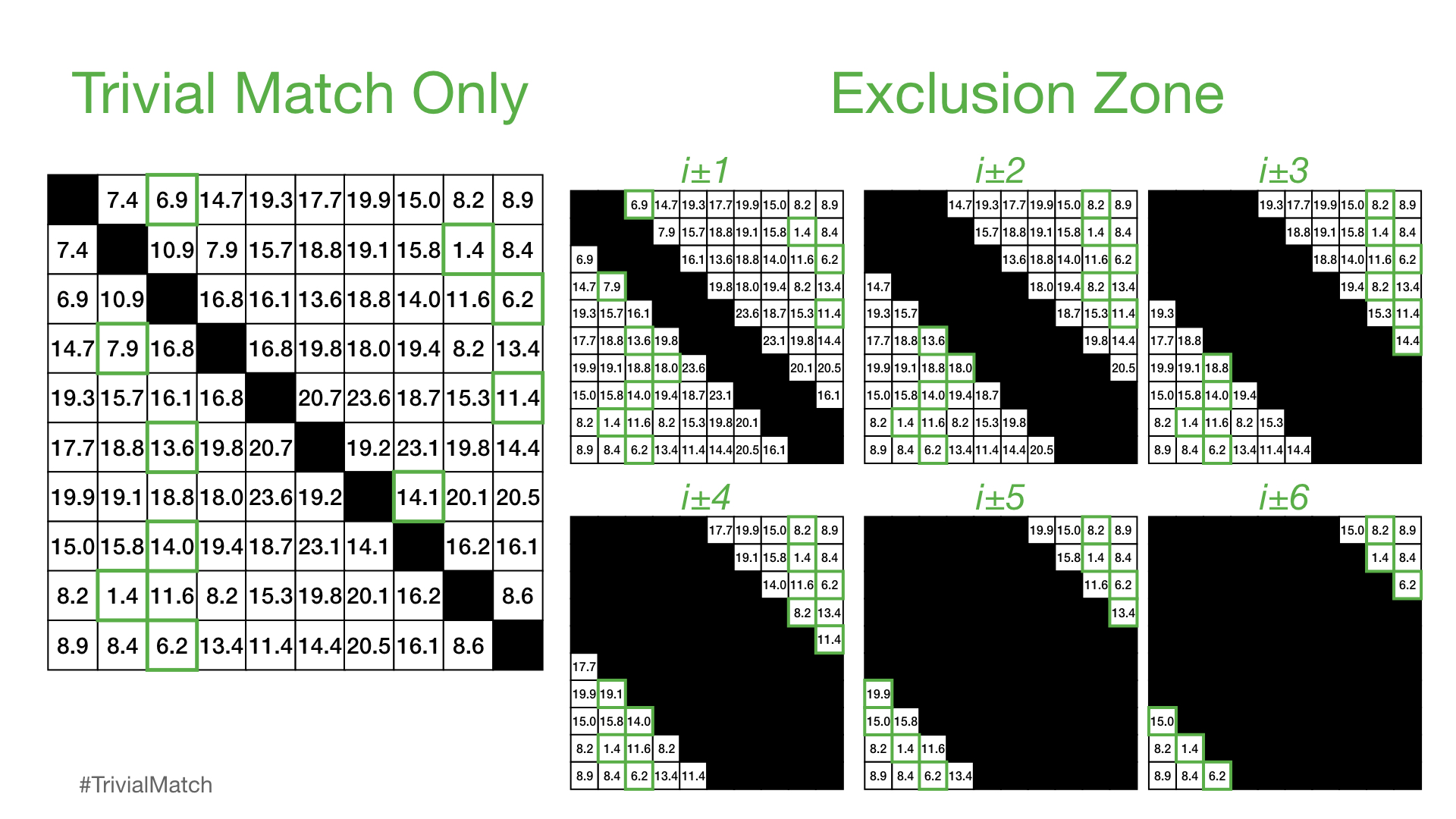
Exclusion Zone

然而，在实践中发现，i ± int(np.ceil(m / 4)) 的排除区工作良好（其中 m 是子序列窗口大小），并且在提取ith子序列的矩阵轮廓值之前，该区域中计算出的距离被设置为 np.inf。因此，窗口大小越大，排除区就越大。此外，请注意，由于NumPy索引具有包括起始索引但排除结束索引，因此确保对称排除区的正确方法是：

excl_zone = int(np.ceil(m / 4))
zone_start = i - excl_zone
zone_end = i + excl_zone + 1  # Notice that we add one since this is exclusive
distance_profile[zone_start : zone_end] = np.inf

最后，用户需要更改默认排除区域的情况非常罕见。然而，在极其少见的情况下，排除区域可以通过config.STUMPY_EXCL_ZONE_DENOM参数在STUMPY中全局更改，其中所有排除区域的计算为i ± int(np.ceil(m / config.STUMPY_EXCL_ZONE_DENOM))：

import stumpy
from stumpy import config

config.STUMPY_EXCL_ZONE_DENOM = 4  # The exclusion zone is i ± int(np.ceil(m / 4)) and is the same as the default setting
mp = stumpy.stump(T, m)

config.STUMPY_EXCL_ZONE_DENOM = 1  # The exclusion zone is i ± m
mp = stumpy.stump(T, m)

config.STUMPY_EXCL_ZONE_DENOM = np.inf  # The exclusion zone is i ± 0 and is the same as applying no exclusion zone
mp = stumpy.stump(T, m)

资源#

STUMPY 文档

STUMPY 矩阵概况 GitHub 代码库