使用SCRUMP快速近似矩阵概要#

Binder

在 这篇文章中，提出了一种称为“SCRIMP++”的新方法，该方法以增量方式计算矩阵轮廓。当仅需要一个近似矩阵轮廓时，该算法利用矩阵轮廓计算的某些特性大大减少了总计算时间，在本教程中，我们将演示这种方法如何足够满足您的应用。

stumpy 实现了这个方法，用于自连接和 AB 连接在 stumpy.scrump 函数中，并允许在需要更高分辨率输出时轻松优化矩阵剖面。

开始使用#

首先，让我们导入一些我们将用于数据加载、分析和绘图的包。

%matplotlib inline

import pandas as pd
import stumpy
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle

plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')

加载Steamgen数据集#

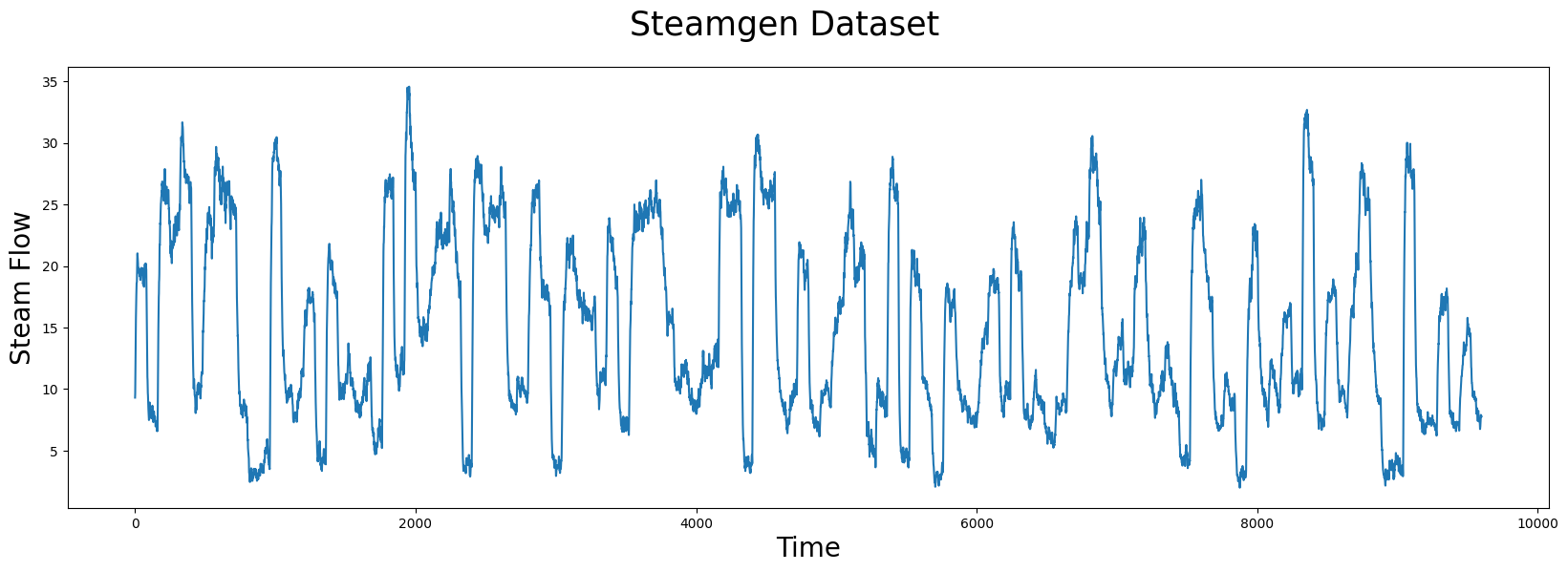
这些数据是使用模糊模型生成的，旨在模拟位于伊利诺伊州香槟的阿博特发电厂的蒸汽发生器。我们感兴趣的数据特征是输出蒸汽流量的遥测，单位为kg/s，数据每三秒“采样”一次，总共有9,600个数据点。

steam_df = pd.read_csv("https://zenodo.org/record/4273921/files/STUMPY_Basics_steamgen.csv?download=1")
steam_df.head()
鼓压力 过剩氧气 水位 蒸汽流量
0 320.08239 2.506774 0.032701 9.302970
1 321.71099 2.545908 0.284799 9.662621
2 320.91331 2.360562 0.203652 10.990955
3 325.00252 0.027054 0.326187 12.430107
4 326.65276 0.285649 0.753776 13.681666

可视化Steamgen数据集#

plt.suptitle('Steamgen Dataset', fontsize='25')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Steam Flow', fontsize='20')
plt.plot(steam_df['steam flow'].values)
plt.show()
_images/c3d73d643029d9a53d31bf169893cd871788d6a1581bc0a98f776425dff90ee9.png

计算真实矩阵剖面#

现在，作为比较的基准，我们将使用 stumpy.stump 函数计算完整的矩阵简介，窗口大小为 m=640。

m = 640
mp = stumpy.stump(steam_df['steam flow'], m)
true_P = mp[:, 0]

fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Motif (Pattern) Discovery', fontsize='25')

axs[0].plot(steam_df['steam flow'].values)
axs[0].set_ylabel('Steam Flow', fontsize='20')
rect = Rectangle((643, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((8724, 0), m, 40, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Matrix Profile', fontsize='20')
axs[1].axvline(x=643, linestyle="dashed")
axs[1].axvline(x=8724, linestyle="dashed")
axs[1].plot(true_P)
plt.show()
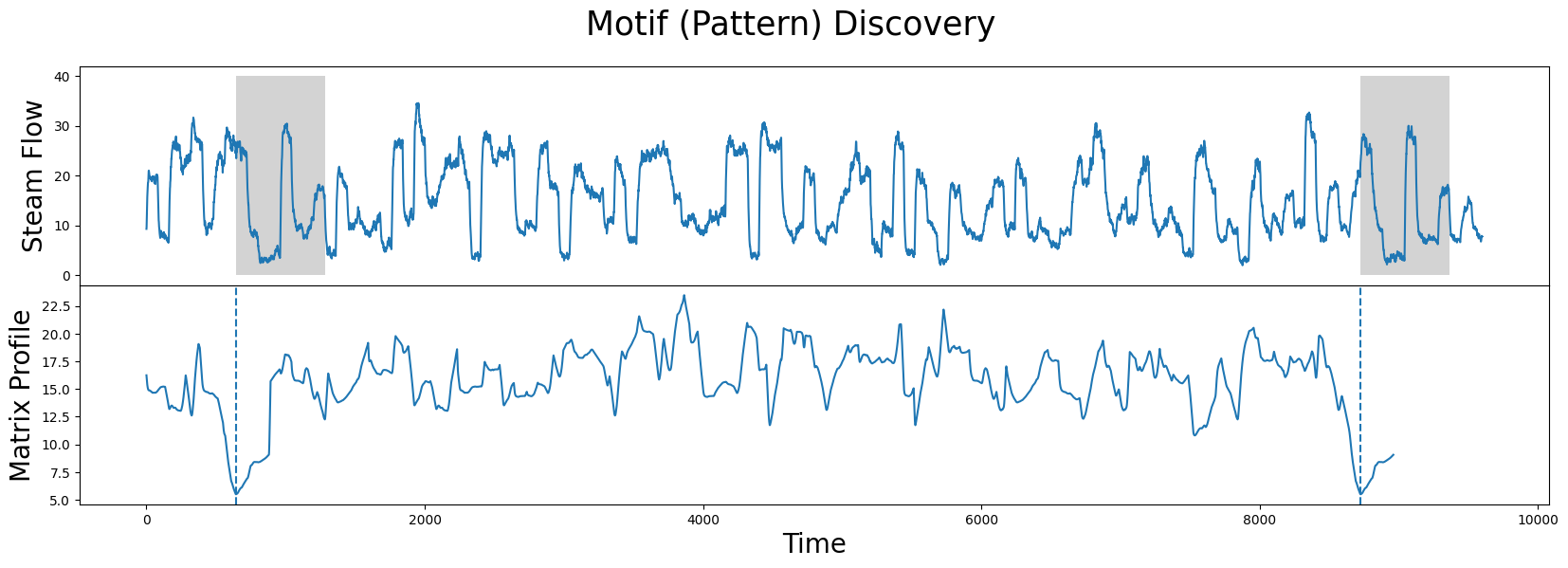
_images/7a24b1de6a56bf4f302f4d265cc1f9b4852026d236c136ba28d153fc9ef373d8.png

矩阵剖面的全局最小值，用虚线表示，是最重要的模式的索引，即最相似的两个子序列。在许多应用中，使用矩阵剖面时，这两个子序列是最重要的，我们将看到如何使用 stumpy.scrump 在极短的时间内快速得出近似的矩阵剖面。

此外，我们将使用下面的助手函数来直观比较真实的矩阵轮廓（true_P - 通过 stumpy.stump 计算得出）与近似的矩阵轮廓（approx_P - 通过 stumpy.scrump 计算得出）。

def compare_approximation(true_P, approx_P):
    fig, ax = plt.subplots(gridspec_kw={'hspace': 0})

    ax.set_xlabel('Time', fontsize ='20')
    ax.axvline(x=643, linestyle="dashed")
    ax.axvline(x=8724, linestyle="dashed")
    ax.set_ylim((5, 28))
    ax.plot(approx_P, color='C1', label="Approximate Matrix Profile")
    ax.plot(true_P, label="True Matrix Profile")
    ax.legend()
    plt.show()

在STUMPY版本1.12.0之后添加

可以通过 P_ 属性直接访问矩阵谱距离，通过 I_ 属性访问矩阵谱索引：

mp = stumpy.stump(T, m)
print(mp.P_, mp.I_)  # print the matrix profile and the matrix profile indices

使用SCRUMP计算近似矩阵剖面#

要计算完整的矩阵轮廓，必须计算整个距离矩阵（即所有子序列对之间的成对距离）。然而，stumpy.scrump 是以对角线的方式计算这个距离矩阵，但只使用所有对角线的一个子集（因此，仅使用所有距离的一个子集）。您希望沿对角线计算多少个成对距离由 percentage 参数控制。计算的距离越多，近似值就越好，但这也意味着更高的计算成本。选择 1.0 的值，即所有距离的100%，会产生完整精确的矩阵轮廓（相当于 stumpy.stump 的输出）。重要的是要注意，即使计算的成对距离较少，也没有成对距离被近似。也就是说，当 percentage <= 1.0 时，您始终保证 approx_P >= true_P，并且在 percentage=1.0 时， approx_P == true_P（即，它是精确的）。

现在，我们来调用 stumpy.scrump 并通过仅计算 1% 的所有距离（即 percentage=0.01）来近似完整的矩阵特征：

approx = stumpy.scrump(steam_df['steam flow'], m, percentage=0.01, pre_scrump=False)

有几点需要注意。首先，我们传入了一个 pre_scrump 参数，这是 stumpy.scrump 的预处理步骤，当设置为 True 时，可以大大改善近似效果。目前，我们为演示目的关闭了预处理步骤，并将在下一节中重新讨论它。其次， stumpy.scrump 初始化并返回一个 scrump 对象，而不是直接返回矩阵轮廓，我们将看到这为什么有用。

要获取第一个近似值（即，从所有距离的1%计算得到的矩阵轮廓），我们只需调用 .update() 方法：

approx.update()

我们可以通过 .P_ 和 .I_ 属性访问更新后的矩阵剖面和矩阵剖面索引：

approx_P = approx.P_

请记住，近似矩阵轮廓是通过随机计算沿着一部分对角线的距离来计算的。因此，每次通过调用 stumpy.scrump 初始化一个新的 scrump 对象时，这将随机打乱计算距离的顺序，这不可避免地导致不同的近似矩阵轮廓（除非 percentage=1.0）。根据您的用例，为了确保可重复的结果，您可以考虑在调用 stumpy.scrump 之前设置随机种子：

seed = np.random.randint(100000)
np.random.seed(seed)
approx = stumpy.scrump(steam_df['steam flow'], m, percentage=0.01, pre_scrump=False)

接下来，让我们在 true_P 上绘制 approx_P 以查看它们的比较效果： 

compare_approximation(true_P, approx_P)
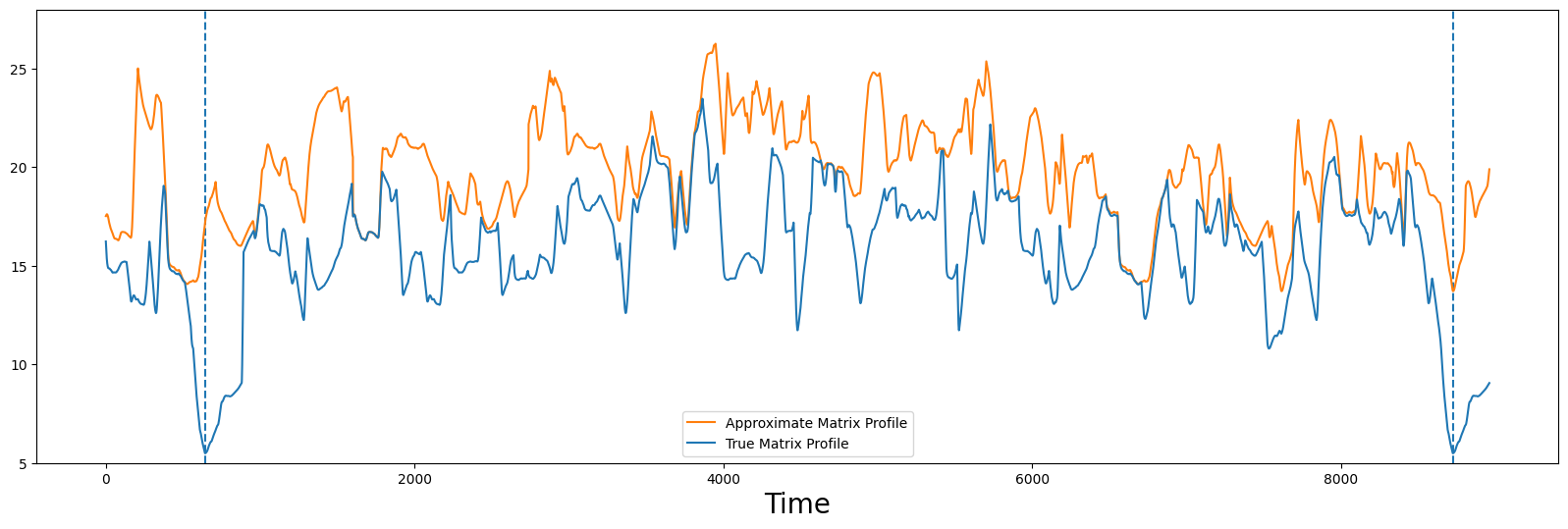
_images/5cbfd34acaa6f56c58b0f2356cf2615d1375fee0e9aca1d417c8c999e0578fb9.png

我们可以看到，这个近似（橙色）还远不完美，但两者之间确实有一些相似之处。然而，该近似中的最低点仍然与真实的最小值不对应。

优化矩阵轮廓#

然而，我们可以通过再调用 .update() 九次（即 10 * 0.01 = 0.10）来逐步改进近似值，因此我们的新近似矩阵轮廓将大约使用完整距离矩阵中所有成对距离的10%进行计算。

for _ in range(9):
    approx.update()
    
approx_P = approx.P_

compare_approximation(true_P, approx_P)
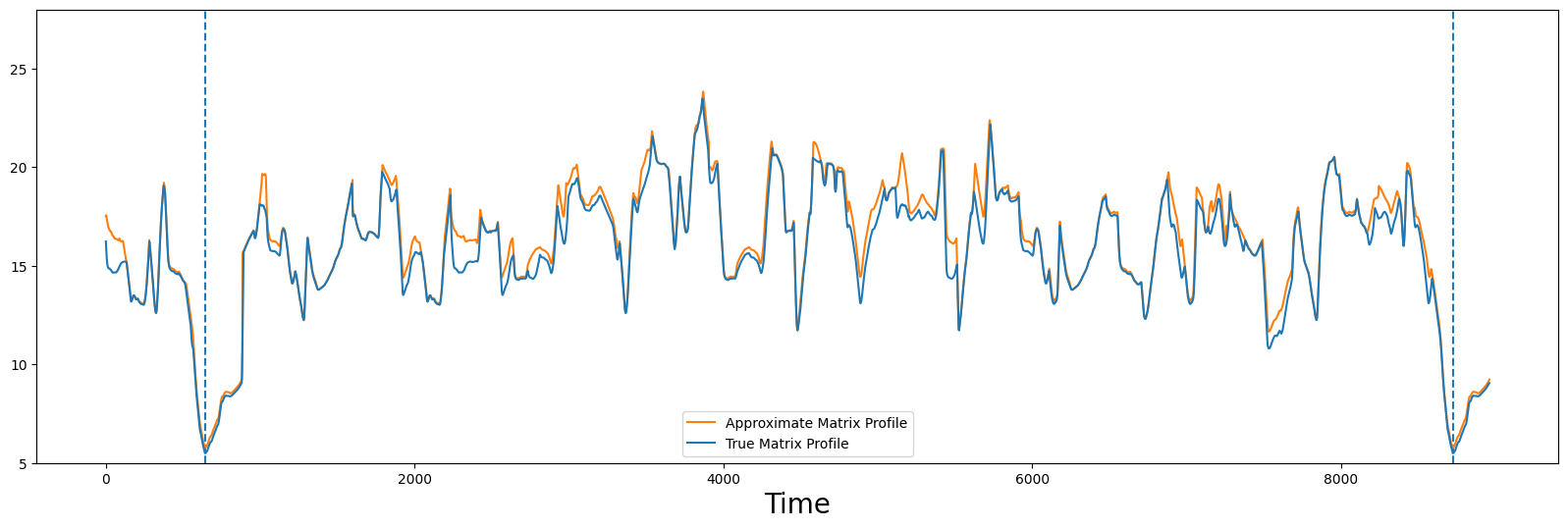
_images/297ca8bc4e8d0811a598e1e4bc38d6d0714c527ba86f5d92586910add0d1f111.png

现在，这个结果更具说服力，而且只计算了所有成对距离的10%！我们可以看到这两个轮廓非常相似，特别是像全局最小值这样的重要特征几乎处于相等的位置，如果不是相等的话。对于大多数应用来说，这已经足够，因为几点的偏移通常并不重要，而且必须计算的距离数量减少了十倍！实际上，我们可以做得更好！

预处理的力量#

到目前为止，我们只运行了 stumpy.scrump 而没有强大的 “PRESCRIMP” 预处理步骤。“PRESCRIMP” 是一种以复杂度 O(n log(n) / s) 对时间序列数据进行预处理的算法，其中 n 是数据点的数量，而 s 被称为采样率。 stumpy.stump 和 stumpy.scrump（没有 PRESCRIMP）都是 O(n^2) 的复杂度，因此，一般来说，预处理是“便宜的”。PRESCRIMP 已经计算了一些成对距离的距离，而采样率控制了计算多少。通常，一个好的值是 s=m/4，与典型的排除区域大小相同，如果你将 None 传递给 scrimp.scrump 函数调用，则会使用这个值。

下面我们将再次近似矩阵轮廓，使用1%的所有对角线，但这次我们将通过设置 pre_scrimp=True 来启用预处理。显然，这将需要更多的时间来计算，因为必须执行更多的计算：

approx = stumpy.scrump(steam_df['steam flow'], m, percentage=0.01, pre_scrump=True, s=None)
approx.update()
approx_P = approx.P_

compare_approximation(true_P, approx_P)
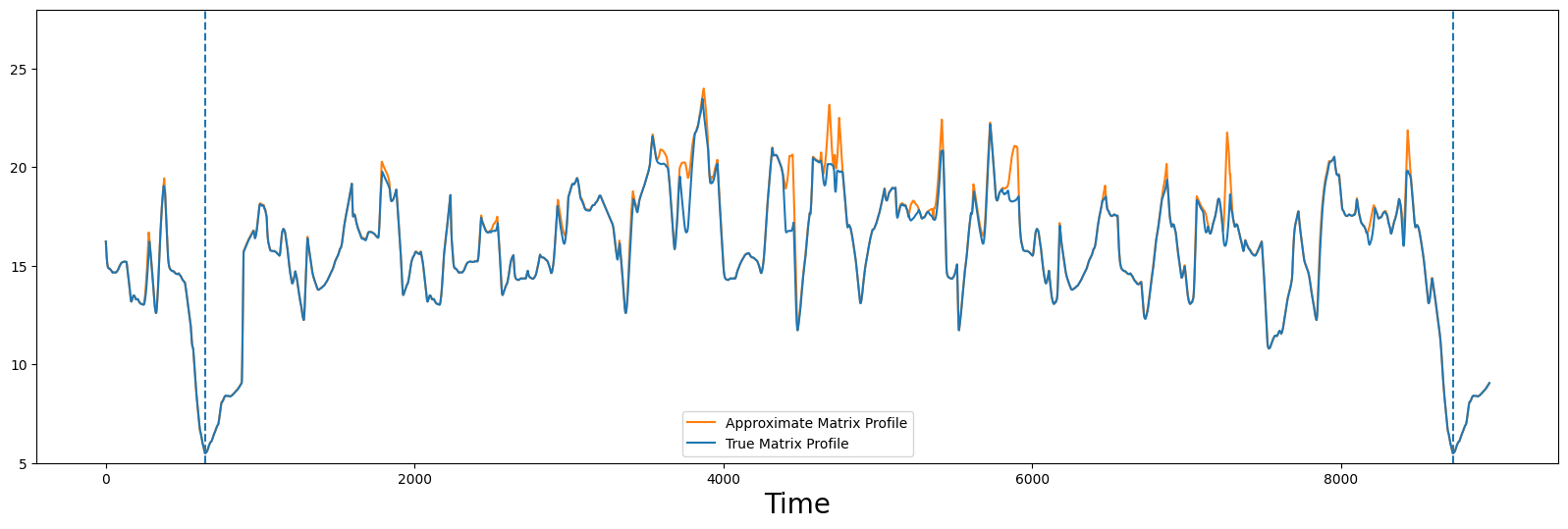
_images/a0563125dbf1a184513d080cb51ee82c34dd134c925fd2c037b7d918b47a2bed.png

然而，人在这个例子中可以看到，经过预处理后，仅计算1%的成对距离（即，只调用一次 .update()），近似矩阵轮廓和真实矩阵轮廓在视觉上几乎无法区分。随着时间序列长度的增加，使用预处理的好处进一步增加。当然，具体取决于您需要分析的时间序列数据的大小和可用的计算资源，计算更高比例的距离可能是值得的，以确保近似结果已收敛。

总结#

就是这样！您已经学习了如何使用 stumpy.scrump 来近似矩阵剖面，并希望能在您的应用中使用近似的矩阵剖面。

资源#

矩阵剖面 XI

STUMPY 文档

STUMPY 矩阵概况 GitHub 代码库