带注释向量的引导模体搜索#
本教程总结了Matrix Profile V论文的研究结果,并复制了一些提供的案例研究。
时间序列模式,如在STUMPY Basics教程中所述,是时间序列中大致重复的子序列。虽然模式发现的概念对许多领域至关重要,但在现实世界中,模式发现的过程通常并不像我们希望的那样干净,并且在大多数实际的模式发现使用中,我们发现一些模式比其他模式更受欢迎。例如,考虑Amazon Customer Reviews Dataset,它包含了来自亚马逊网站的数百万客户评价。如果我们将所有文本评论结合起来,以揭示平台上使用最频繁的词汇,毫无疑问,我们会发现“Amazon”这个词大约位于列表的顶部,可能在几个其他更常用的词汇之后,比如“the”、“and”和“is”。虽然这个结果显而易见,但确实没有用。为了产生更有洞察力的结果,我们需要过滤结果,以排除不太受欢迎或“stop words”,为更受欢迎的词汇让路。
当涉及到时间序列模式发现时,我们可以使用与上述描述相似的方法。虽然我们不能“过滤”时间序列,但我们可以偏好或“引导”识别更有趣的模式,并惩罚那些不那么有趣的模式。本教程将简要介绍注释向量并探讨它们在引导模式搜索中的作用。
什么是注释向量?#
注释向量包含介于0.0和1.0之间的实值数(包括0.0和1.0),可以用来区分时间序列中重要和不重要的子序列(0表示不理想的子序列,1表示理想的子序列)。时间序列的注释向量可以与矩阵剖面结合形成修正后的矩阵剖面,我们可以用它来识别理想的模式。修正后的矩阵剖面可以使用以下公式获得:
其中 \(CMP\) 是修正后的矩阵轮廓, \(MP\) 是原始未更改的矩阵轮廓, \(AV\) 是注释向量,而 \(max(MP)\) 是原始矩阵轮廓的最大值。 本质上,这个公式通过将不希望的距离向允许的最大矩阵轮廓值 \(max(MP)\) 进行偏移,来转换原始矩阵轮廓,从而消除/弱化那些对应的子序列作为潜在的模式。
开始使用#
让我们导入需要加载、分析和绘制数据的包。
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
import stumpy
plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')
血红蛋白浓度数据集#
考虑由 UCLA 医疗中心生产的 fNIRS 脑成像数据集。 fNIRS,或 功能性近红外光谱,是一种用于测量大脑中血红蛋白浓度的光学成像技术。
df = pd.read_csv('https://zenodo.org/record/5045218/files/hemoglobin.csv?download=1')
df = df[6000:14000]
df = df.reset_index(drop=True)
df.head()
| 血红蛋白浓度 | 传感器加速度 | |
|---|---|---|
| 0 | 4578.0 | 7861.0 |
| 1 | 4579.0 | 8008.0 |
| 2 | 4580.0 | 7959.0 |
| 3 | 4581.0 | 7959.0 |
| 4 | 4582.0 | 7959.0 |
该数据集包含两列:血红蛋白浓度和传感器加速度数据,后者我们稍后会讨论。我们可以首先可视化血红蛋白浓度的时间序列。
plt.plot(df['Hemoglobin Concentration'])
plt.xlabel('Time', fontsize="20")
plt.ylabel('Intensity', fontsize="20")
plt.title('Hemoglobin Concentration', fontsize="30")
plt.show()
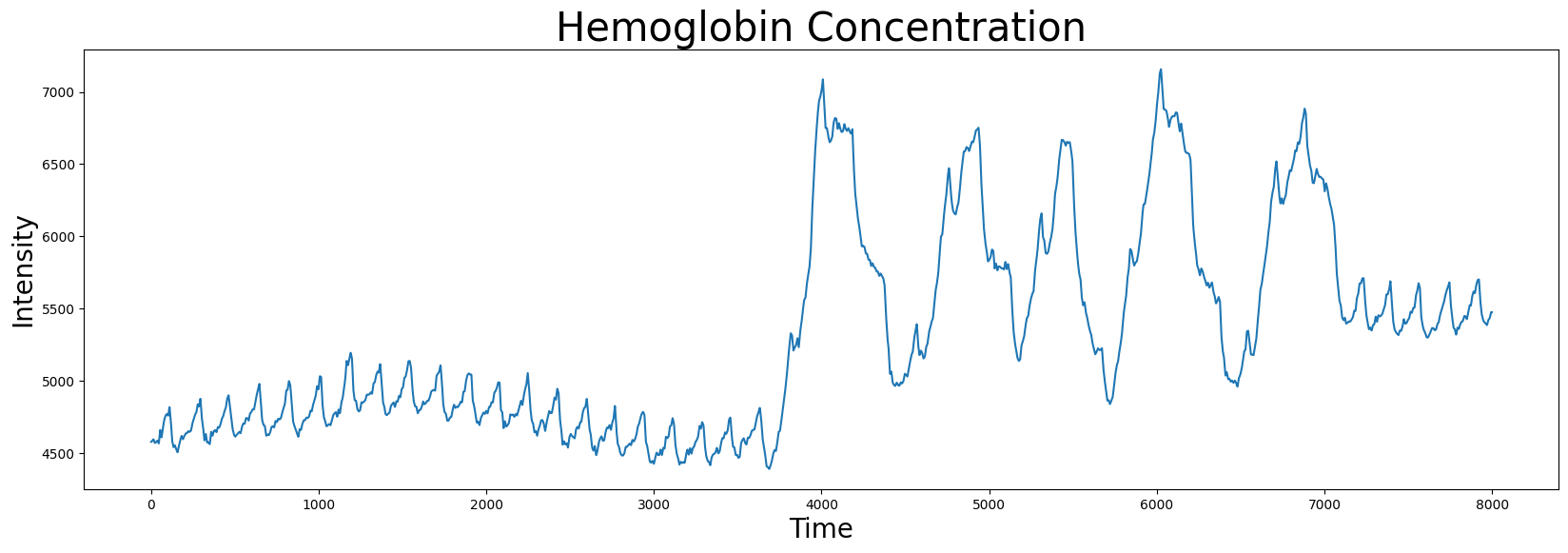
我们可以使用 stumpy.stump 函数来计算这个时间序列的矩阵轮廓,并确定其最近邻的索引位置:
m = 600
mp = stumpy.stump(df['Hemoglobin Concentration'], m)
motif_idx = np.argmin(mp[:, 0])
nn_idx = mp[motif_idx, 1]
现在我们知道了图案/最近邻对的索引位置,我们可以将它们一起可视化:
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Motif (Pattern) Discovery', fontsize='30')
axs[0].plot(df['Hemoglobin Concentration'])
axs[0].set_ylabel('Intensity', fontsize='20')
rect = Rectangle((motif_idx, 4000), m, 4000, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((nn_idx, 4000), m, 4000, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Matrix Profile', fontsize='20')
axs[1].axvline(x=motif_idx, linestyle="dashed")
axs[1].axvline(x=nn_idx, linestyle="dashed")
axs[1].plot(mp[:, 0])
plt.show()
plt.show()

在没有进一步上下文的情况下,结果看起来正是我们想要的。这两个子序列(灰色)实际上是最接近的匹配。
然而,事实证明,上述识别的模式/最近邻对属于时间序列中没有医学意义的一部分。在此期间,大脑成像传感器所捕捉到的只是受试者身体运动引起的红外辐射变化,而不是大脑中的血红蛋白浓度。这可以通过可视化伴随的传感器加速度数据来验证,该数据揭示了在4000和7000时间点之间的快速移动:
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
axs[0].plot(df['Hemoglobin Concentration'])
axs[0].set_ylabel('Intensity', fontsize="20")
axs[0].set_title('Hemoglobin Concentration', fontsize="30")
axs[1].plot(df['Sensor Acceleration'])
axs[1].set_ylabel("Sensor\nAcceleration", fontsize="20")
axs[1].set_xlabel("Time", fontsize="20")
rect = Rectangle((3500, 6200), 3750, 3000, facecolor='lightgrey')
axs[1].add_patch(rect)
plt.show()

那么,在给定这些数据的情况下,我们如何排除这个不理想的高方差区间(灰色)?换句话说,我们如何从这个传感器加速度数据中生成一个注释向量,以保持理想区域并移除不理想区域?
我们可以通过简单地计算传感器加速度数据的滑动方差来实现这一点:
variance = pd.Series(df['Sensor Acceleration']).rolling(m).var().dropna().values
然后找到局部方差异常高的区间(即由于测试对象的物理移动)并在这些区域将我们的注释向量设置为零。同样,如果局部方差小于说, 10000,那么这表示一个可靠的区域,因此我们将其注释为我们注释向量中的1.0:
annotation_vector = (variance < 10000).astype(np.float64)
请注意,注释向量和矩阵剖面应该具有完全相同的长度。接下来,让我们组合这些信息,看看它的样子:
fig, axs = plt.subplots(3, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle("Annotation Vector Generation", fontsize="30")
axs[0].plot(df["Sensor Acceleration"])
axs[0].set_ylabel("Sensor\nAcceleration", fontsize="20")
axs[1].plot(variance)
axs[1].set_ylabel("Variance", fontsize="20")
axs[2].plot(annotation_vector)
axs[2].set_ylabel("Annotation\nValue", fontsize="20")
axs[2].set_xlabel('Time', fontsize="20")
plt.show()
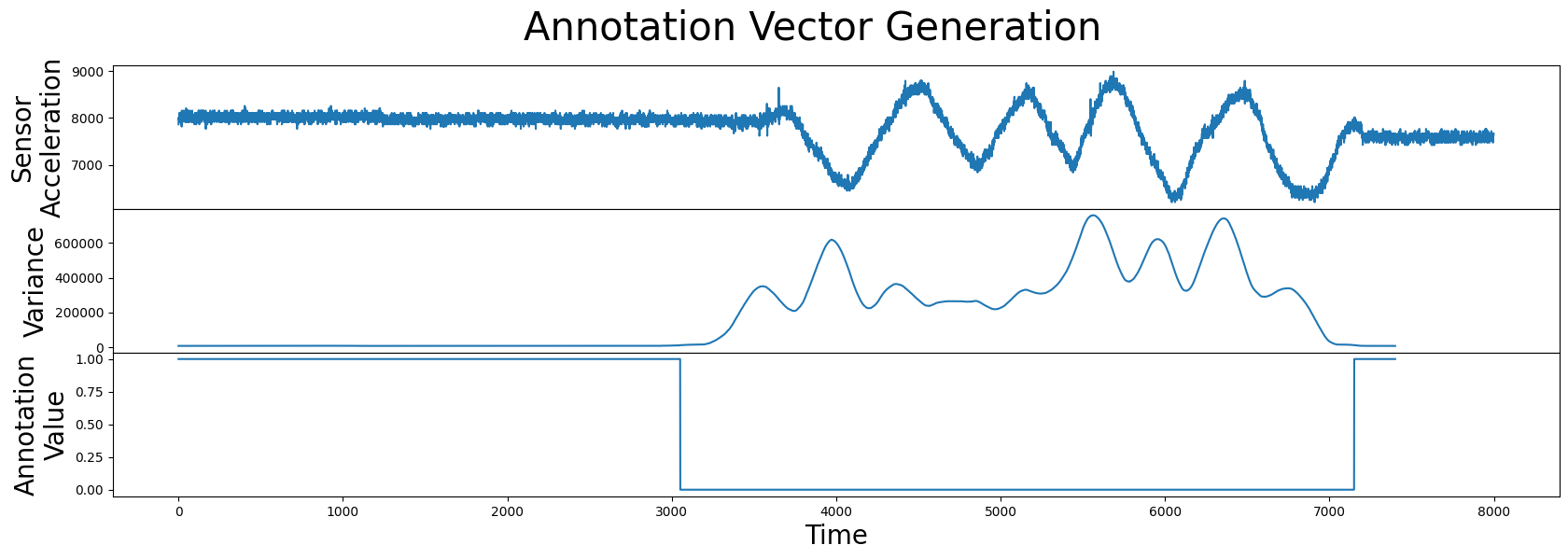
太好了!现在我们有一个注释向量,可以用来排除物理运动的区域,我们可以使用之前介绍的公式来计算校正后的矩阵轮廓:
corrected_mp = mp[:, 0] + ((1 - annotation_vector) * np.max(mp[:, 0]))
我们可以绘制修正后的矩阵轮廓,以看到原始矩阵轮廓是如何被注释向量改变的:
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Matrix Profile Comparison', fontsize="30")
axs[0].plot(mp[:, 0], linestyle='--')
axs[0].plot(corrected_mp, color='C1', linewidth=3)
axs[0].set_ylabel("(Corrected)\nMatrix Profile", fontsize="20")
axs[1].plot(annotation_vector)
axs[1].set_xlabel("Time", fontsize="20")
axs[1].set_ylabel("Annotation\nValue", fontsize="20")
plt.show()
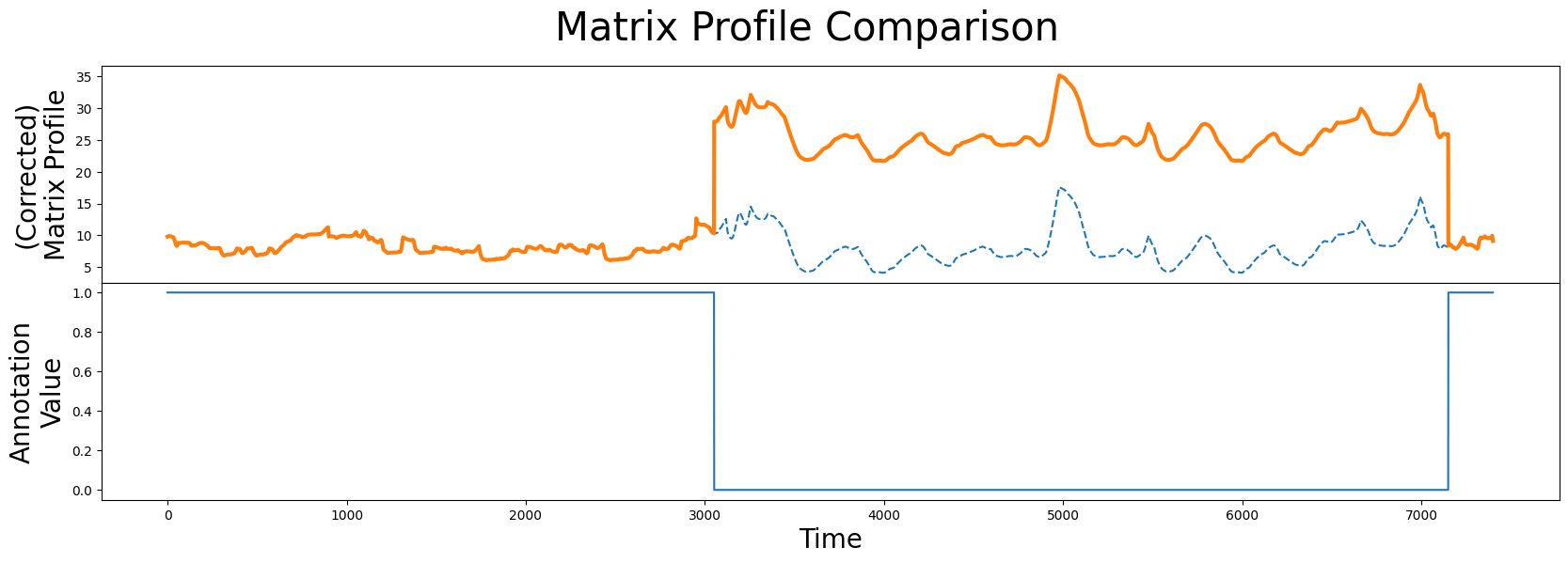
正如我们所看到的,修正后的矩阵轮廓(橙色线)在运动区域附近显著提升。得益于惩罚区域(实心蓝线),原始未修改的矩阵轮廓(虚线)中的最低点不再位于测试对象实际运动的区间内。现在,我们可以使用这个修正后的矩阵轮廓代替我们原来的矩阵轮廓来定位我们的主要模式,就像我们之前做的那样:
motif_idx = np.argmin(corrected_mp)
nn_idx = mp[motif_idx, 1]
并绘制结果:
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Motif (Pattern) Discovery', fontsize='30')
axs[0].plot(df['Hemoglobin Concentration'])
axs[0].set_ylabel('Intensity', fontsize='20')
rect = Rectangle((motif_idx, 4000), m, 4000, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((nn_idx, 4000), m, 4000, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Corrected\nMatrix Profile', fontsize='20')
axs[1].axvline(x=motif_idx, linestyle="dashed")
axs[1].axvline(x=nn_idx, linestyle="dashed")
axs[1].plot(corrected_mp)
plt.show()
plt.show()

正如我们所见,样式/最近邻对(灰色)已向左移动,接近于对应于更理想数据的小峰值,因此,我们成功地将物理运动区域从我们的样式搜索中排除!
在上述例子中,我们生成了一个注释向量,该向量完全忽略了我们不想要的区域。不过,有时我们可能不想完全从主题搜索中移除一个区域,而只是想“劝阻/降低其重要性”。下一个例子探讨了这种情况。
眼电图数据集#
考虑包含左眼电位数据的EOG数据集,采样频率为50 Hz。EOG,或电眼图记录,是一种用于测量人眼前后之间存在的电位的技术。我们可以下载并可视化数据,以更好地理解其趋势:
df = pd.read_csv('https://zenodo.org/record/5045252/files/eog.csv?download=1')
df.head()
| 电势 | |
|---|---|
| 0 | -0.980 |
| 1 | 2.941 |
| 2 | 2.941 |
| 3 | 2.941 |
plt.plot(df['Electric Potential'])
plt.xlabel('Time', fontsize="20")
plt.ylabel('Voltage', fontsize="20")
plt.show()
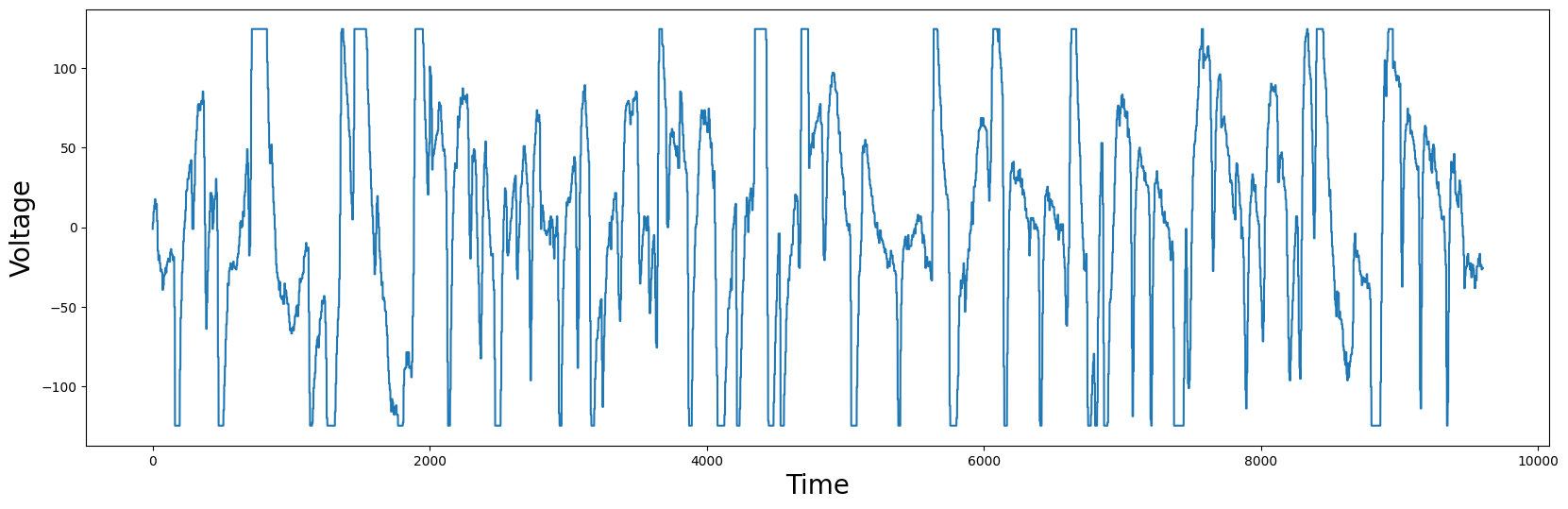
你应该注意到图中的某些点有平坦的顶部或底部。从医学角度来看,这并不反映现实。平坦的顶部和底部仅仅是截断区域,因为测量值超过了浮点数的测量范围。尽管如此,我们仍然可以盲目计算矩阵剖面并定位最佳模式:
m = 450
mp = stumpy.stump(df['Electric Potential'], m)
motif_idx = np.argmin(mp[:, 0])
nn_idx = mp[motif_idx, 1]
并可视化结果:
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Motif (Pattern) Discovery', fontsize='30')
axs[0].plot(df['Electric Potential'])
axs[0].set_ylabel('Voltage', fontsize='20')
rect = Rectangle((motif_idx, -150), m, 300, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((nn_idx, -150), m, 300, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Matrix Profile', fontsize='20')
axs[1].axvline(x=motif_idx, linestyle="dashed")
axs[1].axvline(x=nn_idx, linestyle="dashed")
axs[1].plot(mp[:, 0])
plt.show()
plt.show()
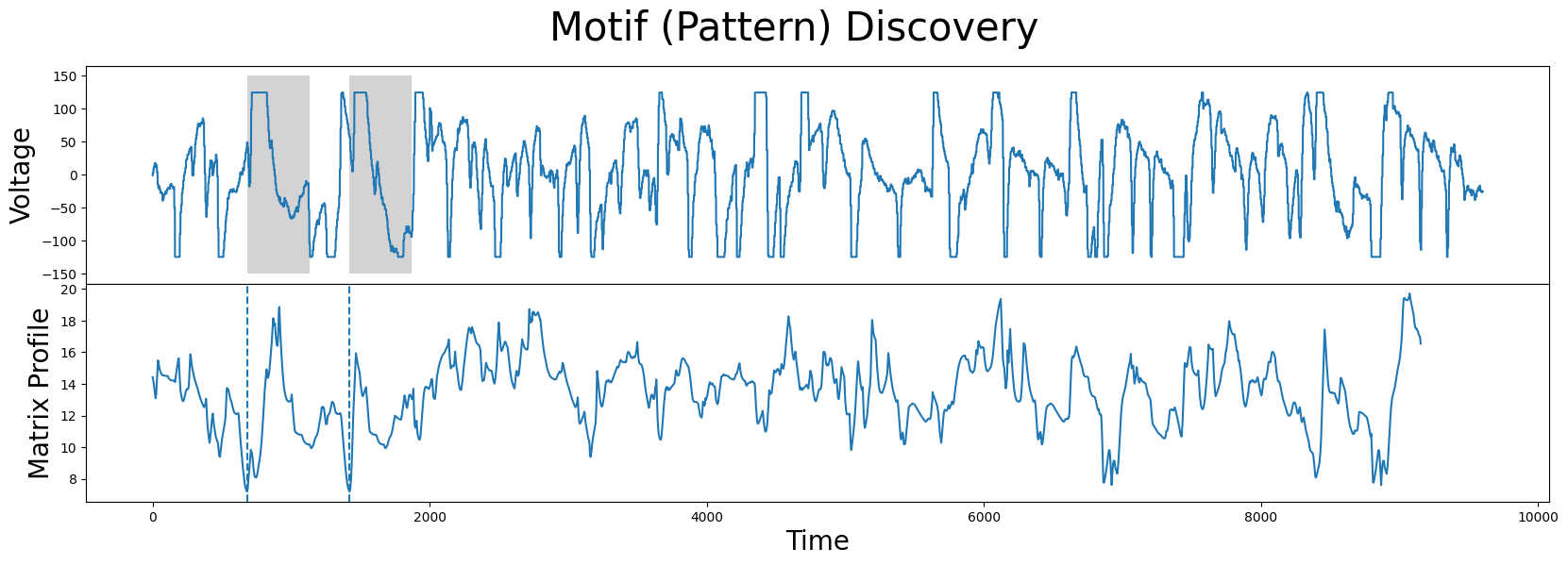
毫不奇怪,图案/最近邻对包含时间序列中最大的平顶。这是有道理的,因为两个平顶之间的距离非常小。
当然,由于平坦的顶部或底部是电势的实际值不明确的区域,我们希望使其成为一种不太受欢迎的主题。但是,前一个血红蛋白示例与当前示例之间的区别在于,我们并不想完全忽略这些裁剪区域。相反,我们只希望对它们进行轻微惩罚。我们通过构造一个真实值的注释向量来实现这一点,这与前一个示例中限制为仅为0或1的情况不同。因此,对于每个子序列,我们统计与全局最小值或最大值相等的值的数量。数量越高,子序列的注释向量值就设置得越低,反之亦然:
global_min = df["Electric Potential"].min()
global_max = df["Electric Potential"].max()
count_minmax = lambda x: np.count_nonzero(x == global_max) + np.count_nonzero(x == global_min)
annotation_vector = df["Electric Potential"].rolling(m).apply(count_minmax).dropna().values
annotation_vector = 1 - (annotation_vector - np.min(annotation_vector)) / np.max(annotation_vector)
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
axs[0].plot(df["Electric Potential"])
axs[0].set_ylabel("Voltage", fontsize="20")
axs[1].plot(annotation_vector)
axs[1].set_ylabel("Annotation\nValue", fontsize="20")
axs[1].set_xlabel('Time', fontsize="20")
plt.show()
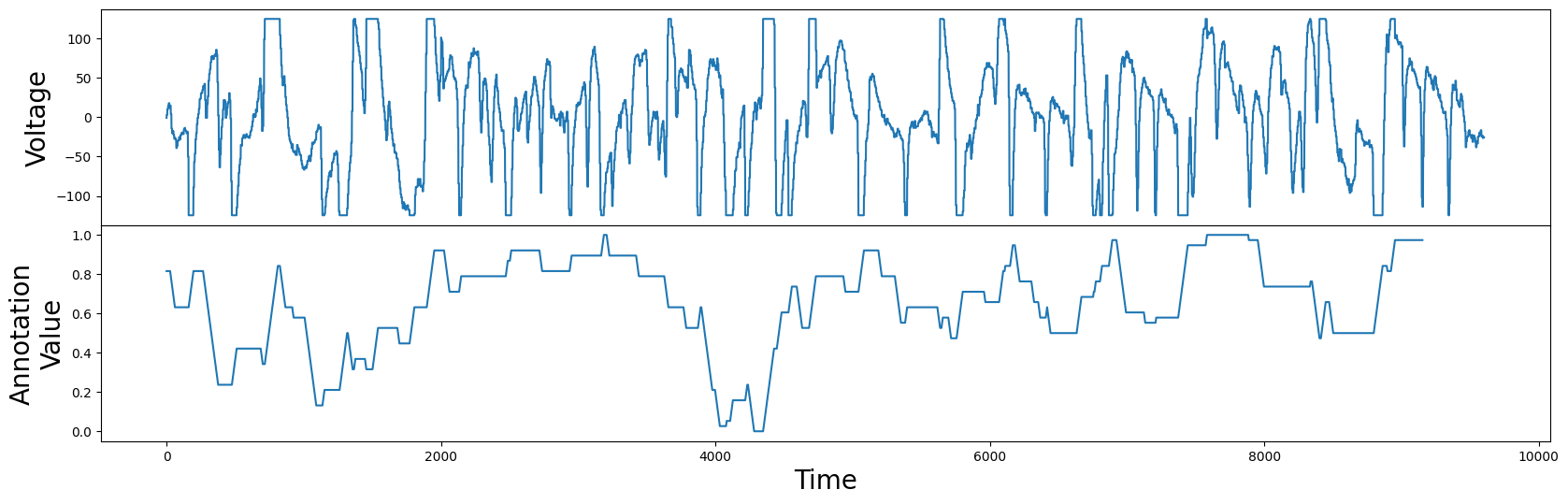
现在我们有一个注释向量,在包含平顶或平底的子序列中较低,而在没有平顶或平底的地方较高。与为血红蛋白浓度示例生成的注释向量相比,这个注释向量可以取0到1之间的任何实值数。我们现在可以像之前一样,使用这个注释向量生成校正后的矩阵剖面:
corrected_mp = mp[:, 0] + ((1 - annotation_vector) * np.max(mp[:, 0]))
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Matrix Profile Comparison', fontsize="30")
axs[0].plot(mp[:, 0], linestyle='--')
axs[0].plot(corrected_mp, color='C1', linewidth=3)
axs[0].set_ylabel("(Corrected)\nMatrix Profile", fontsize="20")
axs[1].plot(annotation_vector)
axs[1].set_xlabel("Time", fontsize="20")
axs[1].set_ylabel("Annotation\nValue", fontsize="20")
plt.show()
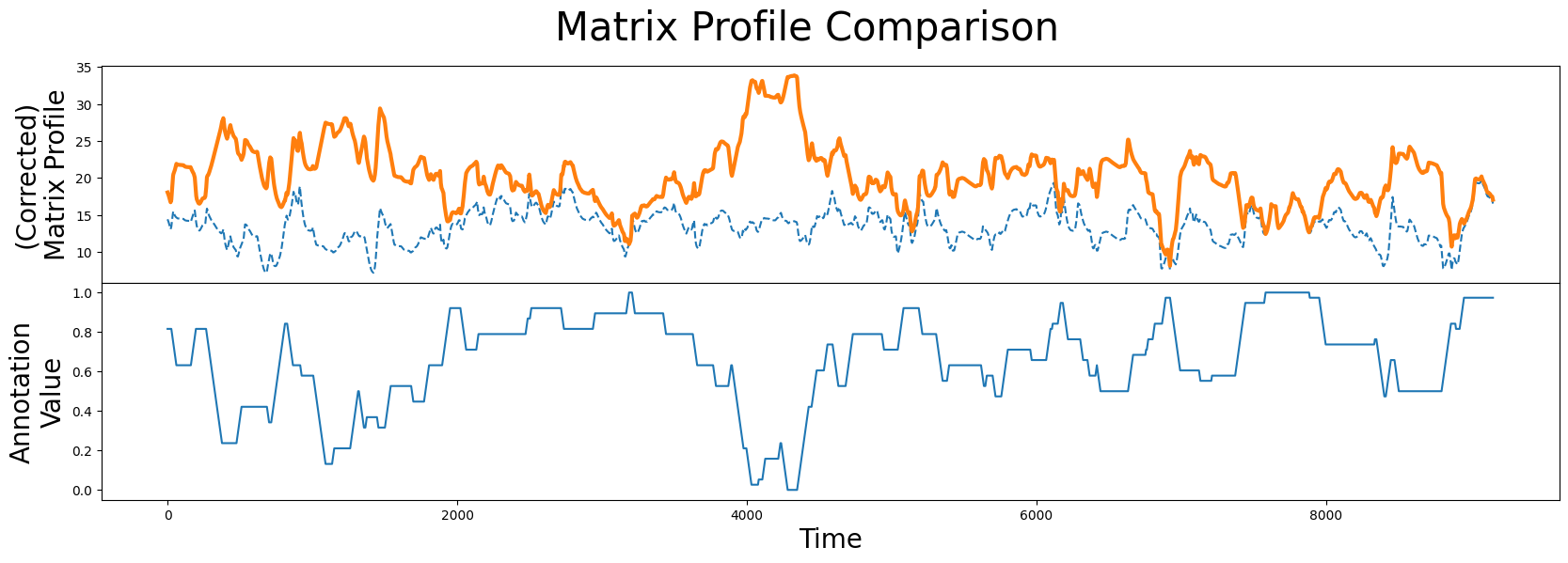
当我们比较原始未改变的矩阵轮廓(虚线)和修正后的矩阵轮廓(橙色线)时,我们清楚地看到具有最低矩阵轮廓值的子序列已经改变。现在我们准备再次使用修正后的矩阵轮廓计算最佳模式:
motif_idx = np.argmin(corrected_mp)
nn_idx = mp[motif_idx, 1]
fig, axs = plt.subplots(2, sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Motif (Pattern) Discovery', fontsize='30')
axs[0].plot(df['Electric Potential'])
axs[0].set_ylabel('Voltage', fontsize='20')
rect = Rectangle((motif_idx, -150), m, 300, facecolor='lightgrey')
axs[0].add_patch(rect)
rect = Rectangle((nn_idx, -150), m, 300, facecolor='lightgrey')
axs[0].add_patch(rect)
axs[1].set_xlabel('Time', fontsize ='20')
axs[1].set_ylabel('Matrix Profile', fontsize='20')
axs[1].axvline(x=motif_idx, linestyle="dashed")
axs[1].axvline(x=nn_idx, linestyle="dashed")
axs[1].plot(corrected_mp)
plt.show()
plt.show()
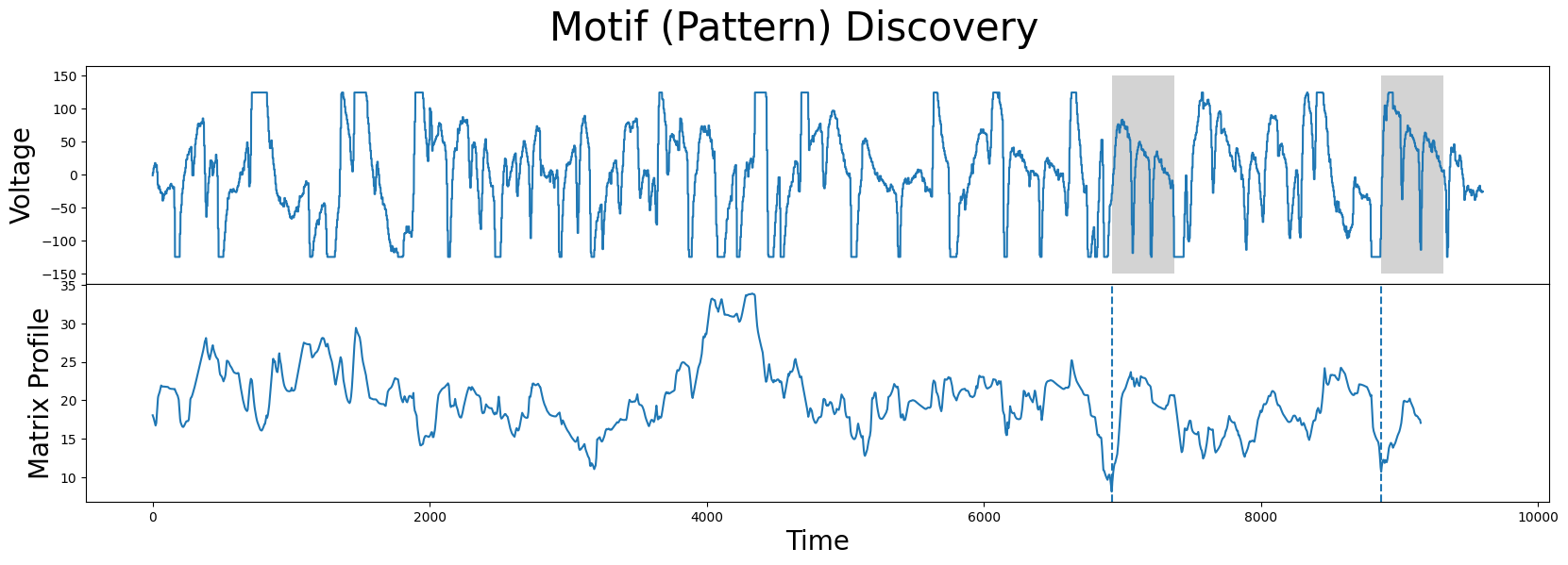
正如我们所看到的,新图案(灰色)不再位于平顶或平底区域,并且,我们再次成功地引导了我们的图案搜索,以找到更有趣的图案。
总结#
就这样!你现在已经学习了带注释向量的引导图案搜索的基础知识,你现在可以利用这个简单的方法并在自己的项目中使用它。祝你编码愉快!
