时间序列链#
使用锚定时间序列链(ATSC)预测网络查询数据#
这个例子改编自网络查询量案例研究:“网络如丛林:共进化在线活动的非线性动力系统”,并利用了矩阵剖面 VII研究论文的主要收获。
开始使用#
让我们导入需要加载、分析和绘制数据的包。
%matplotlib inline
import pandas as pd
import numpy as np
import stumpy
from scipy.io import loadmat
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle, FancyArrowPatch
import itertools
plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')
什么是时间序列链?#
时间序列链可以非正式地视为随时间演化或漂移的主题。下图说明了时间序列主题(左侧)和时间序列链(右侧)之间的区别。
x = np.random.rand(20)
y = np.random.rand(20)
n = 10
motifs_x = 0.5 * np.ones(n) + np.random.uniform(-0.05, 0.05, n)
motifs_y = 0.5 * np.ones(n) + np.random.uniform(-0.05, 0.05, n)
sin_x = np.linspace(0, np.pi/2, n+1)
sin_y = np.sin(sin_x)/4
chains_x = 0.5 * np.ones(n+1) + 0.02 * np.arange(n+1)
chains_y = 0.5 * np.ones(n+1) + sin_y
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].scatter(x, y, color='lightgrey')
axes[0].scatter(motifs_x, motifs_y, color='red')
axes[1].scatter(x, y, color='lightgrey')
axes[1].scatter(chains_x[0], chains_y[0], edgecolor='red', color='white')
axes[1].scatter(chains_x[1:n], chains_y[1:n], color='red')
axes[1].scatter(chains_x[n], chains_y[n], edgecolor='red', color='white', marker='*', s=200)
plt.show()
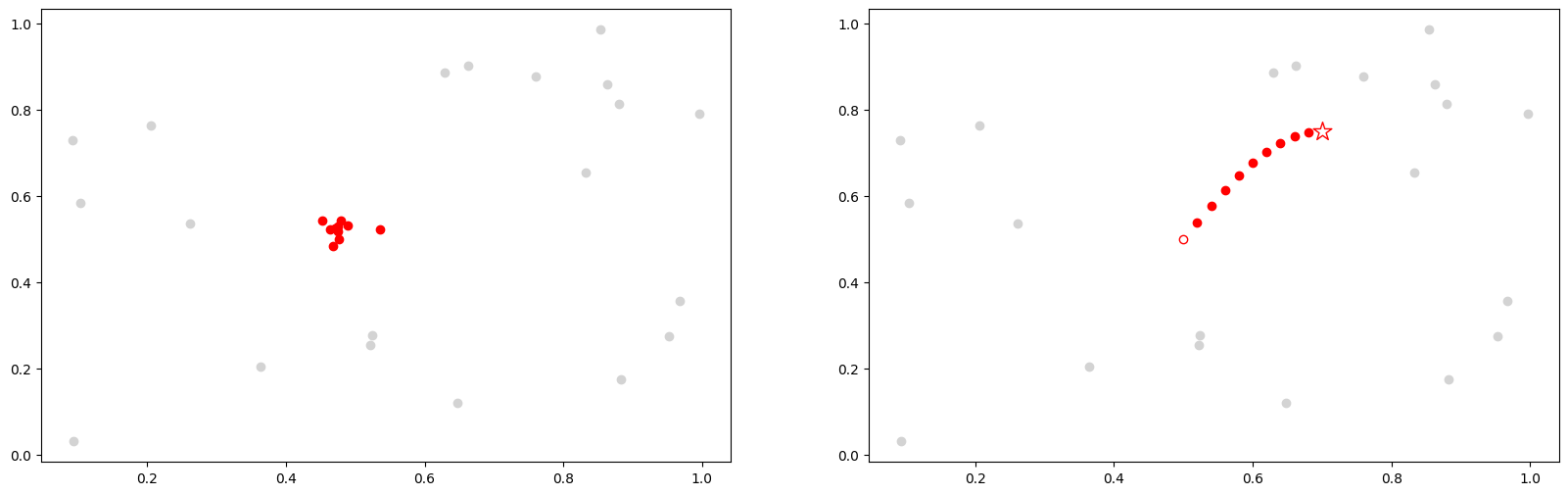
上述,我们将时间序列子序列可视化为高维空间中的点。左侧显示的是时间序列模式,可以被视为一个逼近理想模型的点的集合。相反,右侧描绘的是时间序列链,可以被视为空间中点的演变轨迹。这里,开放的红色圆圈代表链中的第一个链接,即锚。模式和链都有一个特性,即每个子序列与其最近邻相对接近。然而,模式集(左侧)也具有相对较小的直径。相对而言,链中的点集合(右侧)的直径要大于每个成员与其最近邻的平均距离,而且,链具有重要的方向性特性。例如,在模式的情况下,如果向模式集中添加一个额外的成员,其位置也将接近理想模型,但与之前的子序列无关。相对而言,在链的情况下,链中下一个成员的位置将位于最后一个红色圆圈之后,可能在开放的红色星星所在的位置。
简化示例#
改编自Matrix Profile VII论文,考虑以下时间序列:
47, 32, 1, 22, 2, 58, 3, 36, 4, -5, 5, 40
假设子序列的长度为1,并且两个子序列之间的距离仅仅是它们之间的绝对差。为了明确,我们在这里做这些简单和病态的假设纯粹是为了阐明目的;我们实际上目标是更长的子序列长度,并在我们的应用中使用z归一化的欧几里得距离。为了捕捉时间序列链的方向性,我们需要将左侧和右侧最近邻信息存储到左(IL)和右(IR)矩阵轮廓索引中:
索引 |
值 |
左索引 (IL) |
右索引 (IR) |
|---|---|---|---|
1 |
47 |
- |
12 |
2 |
32 |
1 |
8 |
3 |
1 |
2 |
5 |
4 |
22 |
2 |
8 |
5 |
2 |
3 |
7 |
6 |
58 |
1 |
12 |
7 |
3 |
5 |
9 |
8 |
36 |
2 |
12 |
9 |
4 |
7 |
11 |
10 |
-5 |
3 |
11 |
11 |
5 |
9 |
12 |
12 |
40 |
8 |
- |
在这种垂直/转置表示中,index 列显示时间序列中每个子序列的位置,value 列包含我们上面时间序列的原始数字,IL 列显示左矩阵轮廓索引,IR 是右矩阵轮廓索引。例如,IR[2] = 8 意味着 index = 2 的右最近邻(其 value = 32)位于 index = 8(其 value = 36)。类似地,IL[3] = 2 意味着 index = 3 的左最近邻(其 value = 1)位于 index = 2(其 value = 32)。为了更好地可视化左右矩阵轮廓索引,我们使用箭头将时间序列中的每个子序列与其左、右最近邻相连接:
nearest_neighbors = np.array([[1, 47, np.nan, 12],
[2, 32, 1, 8],
[3, 1, 2, 5],
[4, 22, 2, 8],
[5, 2, 3, 7],
[6, 58, 1, 12],
[7, 3, 5, 9],
[8, 36, 2, 12],
[9, 4, 7, 11],
[10, -5, 3, 11],
[11, 5, 9, 12],
[12, 40, 8, np.nan]])
colors = [['C1', 'C1'],
['C2', 'C5'],
['C3', 'C5'],
['C4', 'C4'],
['C3', 'C2'],
['C5', 'C3'],
['C3', 'C2'],
['C2', 'C1'],
['C3', 'C2'],
['C6', 'C1'],
['C6', 'C2'],
['C1', 'C1']]
style="Simple, tail_width=0.5, head_width=6, head_length=8"
kw = dict(arrowstyle=style, connectionstyle="arc3, rad=-.5",)
xs = np.arange(nearest_neighbors.shape[0]) + 1
ys = np.zeros(nearest_neighbors.shape[0])
plt.plot(xs, ys, markerfacecolor="None", markeredgecolor="None", linewidth=0)
x0, x1, y0, y1 = plt.axis()
plot_margin = 5.0
plt.axis((x0 - plot_margin,
x1 + plot_margin,
y0 - plot_margin,
y1 + plot_margin))
plt.axis('off')
for x, y, nearest_neighbor, color in zip(xs, ys, nearest_neighbors, colors):
plt.text(x, y, str(int(nearest_neighbor[1])), color="black", fontsize=20)
# Plot right matrix profile indices
if not np.isnan(nearest_neighbor[3]):
arrow = FancyArrowPatch((x, 0.5), (nearest_neighbor[3], 0.5), color=color[0], **kw)
plt.gca().add_patch(arrow)
# Plot left matrix profile indices
if not np.isnan(nearest_neighbor[2]):
arrow = FancyArrowPatch((x, 0.0), (nearest_neighbor[2], 0.0), color=color[1], **kw)
plt.gca().add_patch(arrow)
plt.show()
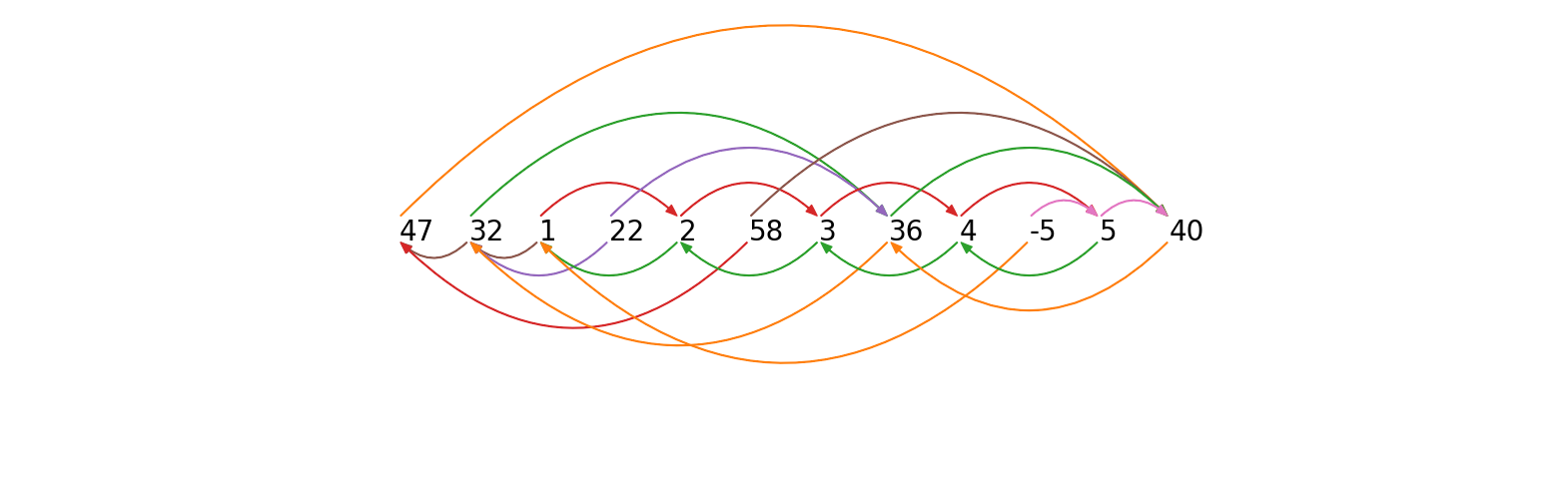
从一个数字指向其右侧最近邻的箭头(上方时间序列中显示的箭头)可以称为向前箭头,而从一个数字指向其左侧最近邻的箭头(下方时间序列中显示的箭头)可以称为向后箭头。根据时间序列链的正式定义(请参阅 Matrix Profile VII 以获取详细定义和讨论),链中每对连续子序列必须由向前箭头和向后箭头连接。一个敏锐的眼光会注意到,我们简化例子中的最长链是:
nearest_neighbors = np.array([[1, 47, np.nan, np.nan],
[2, 32, np.nan, np.nan],
[3, 1, np.nan, 5],
[4, 22, np.nan, np.nan],
[5, 2, 3, 7],
[6, 58, np.nan, np.nan],
[7, 3, 5, 9],
[8, 36, np.nan, np.nan],
[9, 4, 7, 11],
[10, -5, np.nan, np.nan],
[11, 5, 9, np.nan],
[12, 40, np.nan, np.nan]])
colors = [['C1', 'C1'],
['C2', 'C5'],
['C3', 'C5'],
['C4', 'C4'],
['C3', 'C2'],
['C5', 'C3'],
['C3', 'C2'],
['C2', 'C1'],
['C3', 'C2'],
['C6', 'C1'],
['C6', 'C2'],
['C1', 'C1']]
style="Simple, tail_width=0.5, head_width=6, head_length=8"
kw = dict(arrowstyle=style, connectionstyle="arc3, rad=-.5",)
xs = np.arange(nearest_neighbors.shape[0]) + 1
ys = np.zeros(nearest_neighbors.shape[0])
plt.plot(xs, ys, markerfacecolor="None", markeredgecolor="None", linewidth=0)
x0, x1, y0, y1 = plt.axis()
plot_margin = 5.0
plt.axis((x0 - plot_margin,
x1 + plot_margin,
y0 - plot_margin,
y1 + plot_margin))
plt.axis('off')
for x, y, nearest_neighbor, color in zip(xs, ys, nearest_neighbors, colors):
plt.text(x, y, str(int(nearest_neighbor[1])), color="black", fontsize=20)
# Plot right matrix profile indices
if not np.isnan(nearest_neighbor[3]):
arrow = FancyArrowPatch((x, 0.5), (nearest_neighbor[3], 0.5), color=color[0], **kw)
plt.gca().add_patch(arrow)
# Plot left matrix profile indices
if not np.isnan(nearest_neighbor[2]):
arrow = FancyArrowPatch((x, 0.0), (nearest_neighbor[2], 0.0), color=color[1], **kw)
plt.gca().add_patch(arrow)
plt.show()
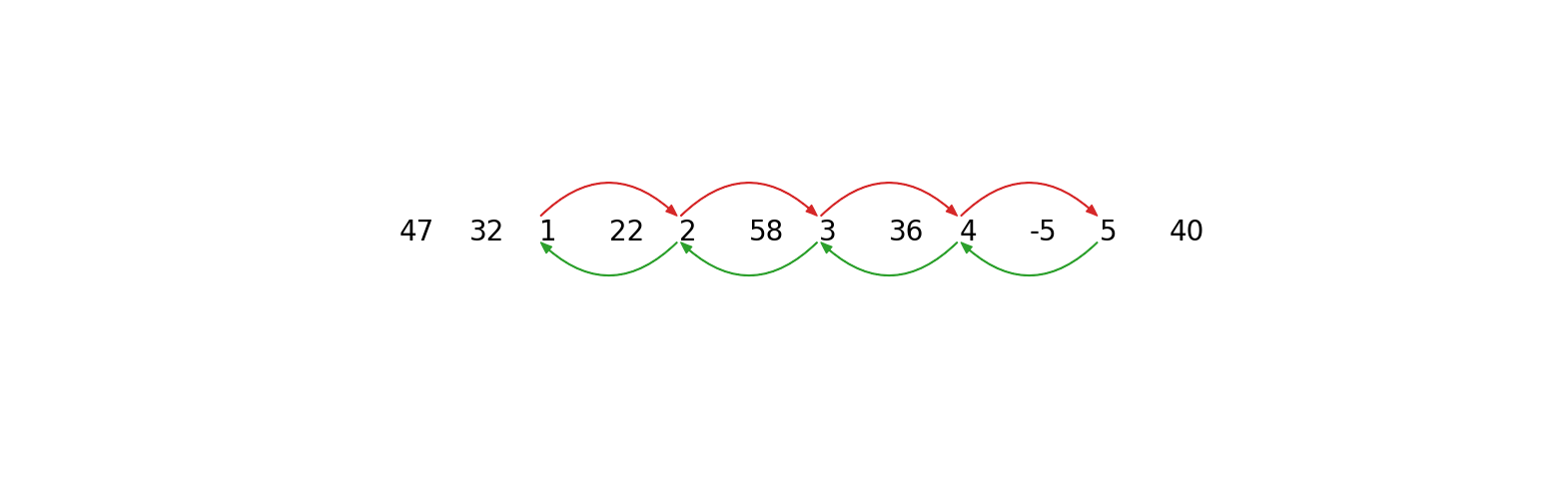
因此,最长的提取链是 1 ⇌ 2 ⇌ 3 ⇌ 4 ⇌ 5。请注意,我们看到数据呈现出逐渐单调增加的趋势,但实际上,漂移的增加或减少可能以任意复杂的方式发生,这可以通过时间序列链方法来检测。漂移的关键组成部分是时间序列必须包含具有明确方向性的链。
STUMPY能够计算:
锚定时间序列链 (ATSC) - 从用户指定的锚(即,特定子序列)增长一个链
全链集合 (ALLC) - 一组锚定的时间序列链(即,每个链都以特定的子序列开始),这些链不被另一个更长的链所包含
无锚时间序列链 - 时间序列中无条件的最长链(请注意,如果有多个相同长度的链,则可能会有多个链,但只返回一个)
那么,这在实时序列的背景下意味着什么呢?我们来看一个来自网络查询数据的真实例子!
获取数据#
我们将看看一个嘈杂的数据集,它的样本不足并且有一个增长趋势,这将完美地说明关于时间序列链的概念。数据包含了十年的GoogleTrend查询量(在2004-2014年期间每周收集)对于关键词Kohl’s,一个美国零售连锁店。首先,我们将下载数据,提取数据,并将其插入到一个pandas数据框中。
df = pd.read_csv("https://zenodo.org/record/4276348/files/Time_Series_Chains_Kohls_data.csv?download=1")
df.head()
| 音量 | |
|---|---|
| 0 | 0.010417 |
| 1 | 0.010417 |
| 2 | 0.010417 |
| 3 | 0.000000 |
| 4 | 0.000000 |
可视化数据#
plt.plot(df['volume'], color='black')
plt.xlim(0, df.shape[0]+12)
color = itertools.cycle(['white', 'gainsboro'])
for i, x in enumerate(range(0, df.shape[0], 52)):
plt.text(x+12, 0.9, str(2004+i), color="black", fontsize=20)
rect = Rectangle((x, -1), 52, 2.5, facecolor=next(color))
plt.gca().add_patch(rect)
plt.show()
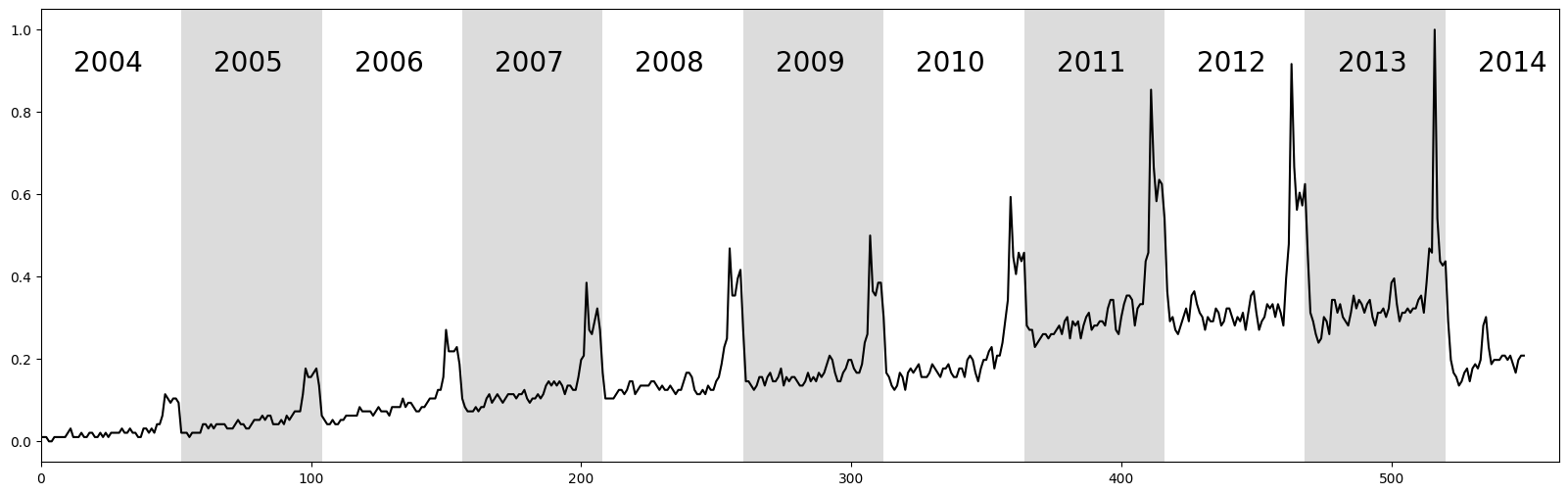
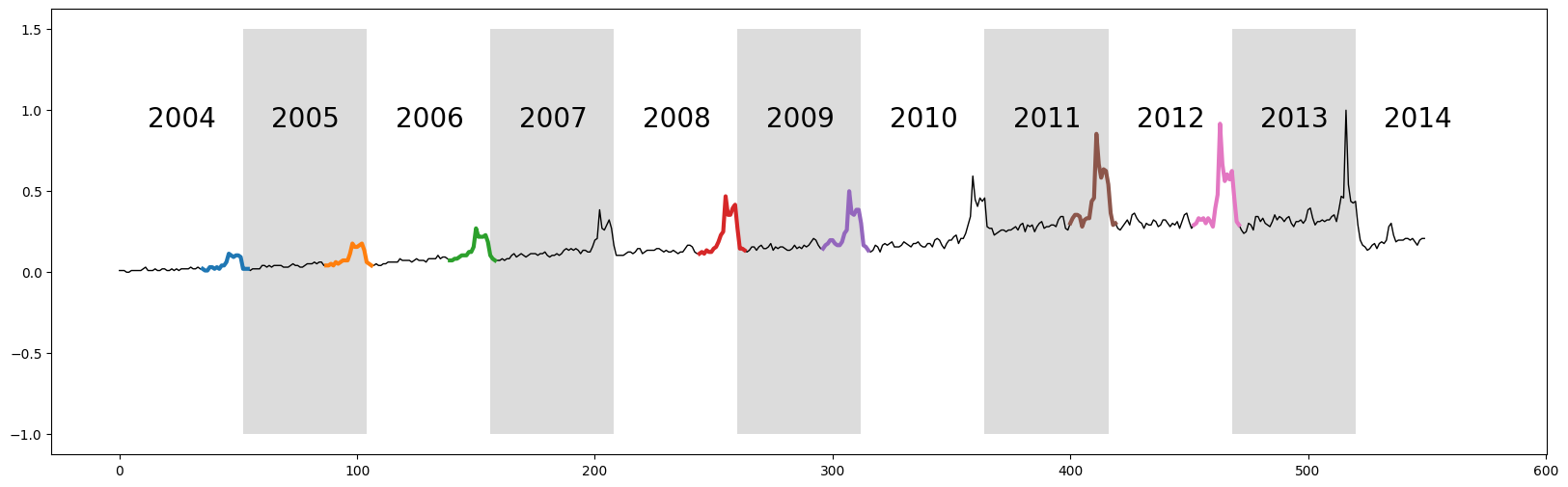
上面的原始时间序列显示了“Kohl's”这个关键词十年的网络查询量,其中每个交替的白色和灰色垂直条带代表从2004年到2014年的52周周期。如图所示,该时间序列具有显著但并不意外的“年末假期高峰”。联系回时间序列链,我们可以看到这个高峰随着时间的推移普遍在增加,因此我们可能能够在计算无锚链时捕捉到这一点。
然而,正如我们上面所学的,为了计算任何时间序列链,我们还需要左侧和右侧矩阵轮廓索引。幸运的是,根据文档字符串,stump 函数不仅返回(双向)矩阵轮廓和 NumPy 数组的第一和第二列中的矩阵轮廓索引,而且第三和第四列分别包含左侧矩阵轮廓索引和右侧矩阵轮廓索引。
计算左矩阵剖面索引和右矩阵剖面索引#
那么,让我们继续计算矩阵轮廓索引,我们将设置窗口大小,m = 20,这大约是一个“隆起”的长度。
m = 20
mp = stumpy.stump(df['volume'], m=m)
计算无锚链#
现在,拥有我们的左边和右边矩阵简介后,我们准备调用全链集合函数,allc,该函数不仅返回全链集合,而且作为额外收益,它还返回无条件最长链,也被称为无锚链。后者实际上是我们最感兴趣的内容。
all_chain_set, unanchored_chain = stumpy.allc(mp[:, 2], mp[:, 3])
在STUMPY版本1.12.0之后添加
在数组切片(即, mp[:, 2], mp[:, 3])的地方,左侧和右侧矩阵剖面索引也可以通过 left_I_ 和 right_I_ 属性分别访问。
mp = stumpy.stump(T, m)
print(mp.left_I_, mp.right_I_) # print the left and right matrix profile indices
此外,您还可以通过 P_ 属性直接访问矩阵轮廓距离,矩阵轮廓索引可以通过 I_ 属性访问。
可视化未锚定链#
plt.plot(df['volume'], linewidth=1, color='black')
for i in range(unanchored_chain.shape[0]):
y = df['volume'].iloc[unanchored_chain[i]:unanchored_chain[i]+m]
x = y.index.values
plt.plot(x, y, linewidth=3)
color = itertools.cycle(['white', 'gainsboro'])
for i, x in enumerate(range(0, df.shape[0], 52)):
plt.text(x+12, 0.9, str(2004+i), color="black", fontsize=20)
rect = Rectangle((x, -1), 52, 2.5, facecolor=next(color))
plt.gca().add_patch(rect)
plt.show()
plt.axis('off')
for i in range(unanchored_chain.shape[0]):
data = df['volume'].iloc[unanchored_chain[i]:unanchored_chain[i]+m].reset_index().values
x = data[:, 0]
y = data[:, 1]
plt.axvline(x=x[0]-x.min()+(m+5)*i + 11, alpha=0.3)
plt.axvline(x=x[0]-x.min()+(m+5)*i + 15, alpha=0.3, linestyle='-.')
plt.plot(x-x.min()+(m+5)*i, y-y.min(), linewidth=3)
plt.show()
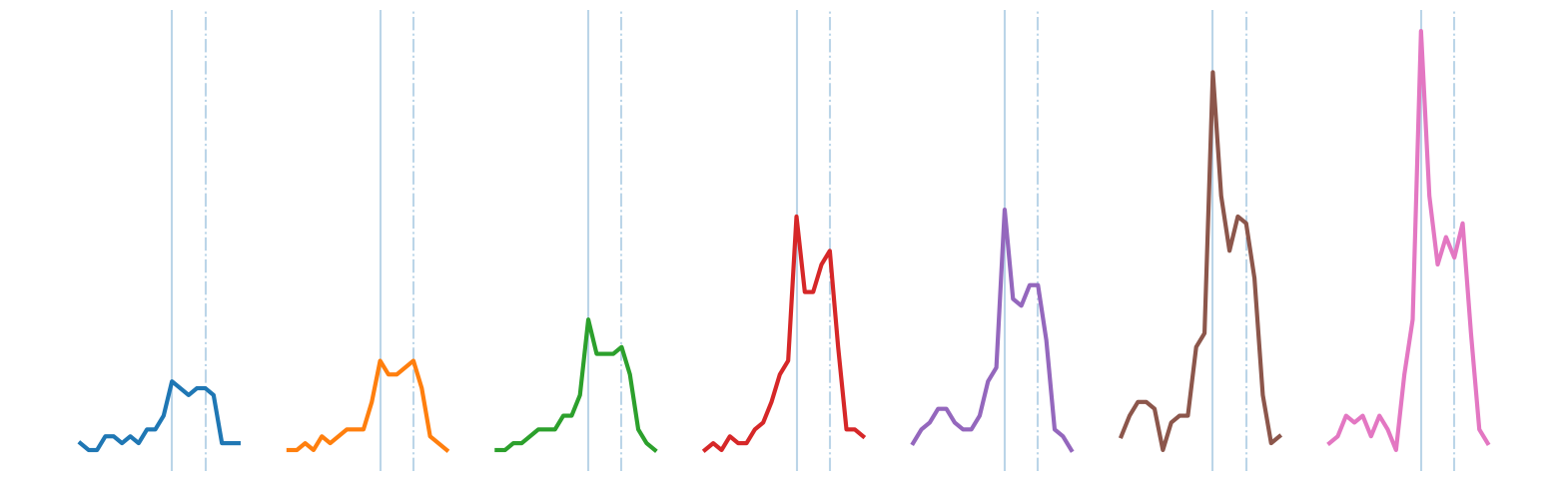
发现的链条显示,在过去十年中,峰值过渡从覆盖感恩节(实线垂直线)和圣诞节(虚线垂直线)之间的平滑峰值,变为一个更集中于感恩节的尖锐峰值。这似乎反映了“网络星期一”的日益重要,这是一种指感恩节后星期一的营销术语。这一短语是由营销公司创造的,目的是为了说服消费者在线购物。该术语于2005年11月28日在一份名为“网络星期一迅速成为一年中最大的在线购物日之一”的新闻稿中首次出现。请注意,这个日期与我们链条中尖锐峰值的首次出现是重合的。
看来我们可能“遗漏”了链条中的几个链接。然而,请注意数据是嘈杂和欠抽样的,而这些“遗漏”的波动过于扭曲,无法符合一般的演变趋势。这个嘈杂的例子实际上说明了时间序列链技术的鲁棒性。正如之前所提到的,我们并不需要“完美”的数据来找到有意义的链条。即使某些链接严重扭曲,发现的链条仍然能够包含所有其他演变的模式。
最后一个考虑因素是链条在预测未来中的潜在用途。人们可以利用链条中不断发展的链接来预测下一个波峰的形状。我们建议读者参考Matrix Profile VII以获取关于此主题的进一步讨论。
总结#
就是这样!您刚刚学习了如何使用矩阵分析指标识别数据中的方向趋势(也称为链)的基本知识,并利用 allc。
