快速模式匹配#
超越矩阵剖面#
在STUMPY的核心中,可以将任何时间序列数据有效地计算出一种称为矩阵剖面的东西,它基本上使用一个固定窗口大小的m沿着整个时间序列扫描,并找到时间序列中每个子序列的确切最近邻。矩阵剖面使您能够确定数据中是否存在任何保留的行为(即,保留的子序列/模式),如果存在,它可以告诉您它们在时间序列中的确切位置。在之前的教程中,我们演示了如何使用STUMPY轻松获得矩阵剖面,学习如何解释结果,并发现有意义的主题和异常。虽然这种蛮力方法在您不知道要寻找什么模式或保留行为时可能非常有用,但对于足够大的数据集,执行这种详尽的成对搜索可能会变得相当昂贵。
然而,如果您已经有一个特定的用户定义模式,那么您实际上不需要计算完整的矩阵剖面!例如,您可能已基于历史股市数据识别出一个有趣的交易策略,并且您想查看该特定模式在过去是否曾在一个或多个股票代码中观察到。在这种情况下,搜索已知模式或“查询”实际上非常简单,并且可以通过使用STUMPY中的精彩stumpy.mass函数快速完成。
在这个简短的教程中,我们将采用一个简单的已知模式(即查询子序列),并在一个独立的时间序列中搜索该模式。让我们开始吧!
开始使用#
让我们导入需要加载、分析和绘制数据的包
%matplotlib inline
import pandas as pd
import stumpy
import numpy as np
import numpy.testing as npt
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')
加载索尼AIBO机器人狗数据集#
时间序列数据(如下),T_df,包含n = 13000个数据点,数据是从Sony AIBO机器狗内部的加速度计收集的,它跟踪了机器人狗从水泥表面走到地毯表面,然后最后回到水泥表面的过程:
T_df = pd.read_csv("https://zenodo.org/record/4276393/files/Fast_Pattern_Searching_robot_dog.csv?download=1")
T_df.head()
| 加速度 | |
|---|---|
| 0 | 0.89969 |
| 1 | 0.89969 |
| 2 | 0.89969 |
| 3 | 0.89969 |
| 4 | 0.89969 |
可视化索尼AIBO机器人狗数据集#
plt.suptitle('Sony AIBO Robot Dog Dataset, T_df', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
plt.plot(T_df)
plt.text(2000, 4.5, 'Cement', color="black", fontsize=20)
plt.text(10000, 4.5, 'Cement', color="black", fontsize=20)
ax = plt.gca()
rect = Rectangle((5000, -4), 3000, 10, facecolor='lightgrey')
ax.add_patch(rect)
plt.text(6000, 4.5, 'Carpet', color="black", fontsize=20)
plt.show()
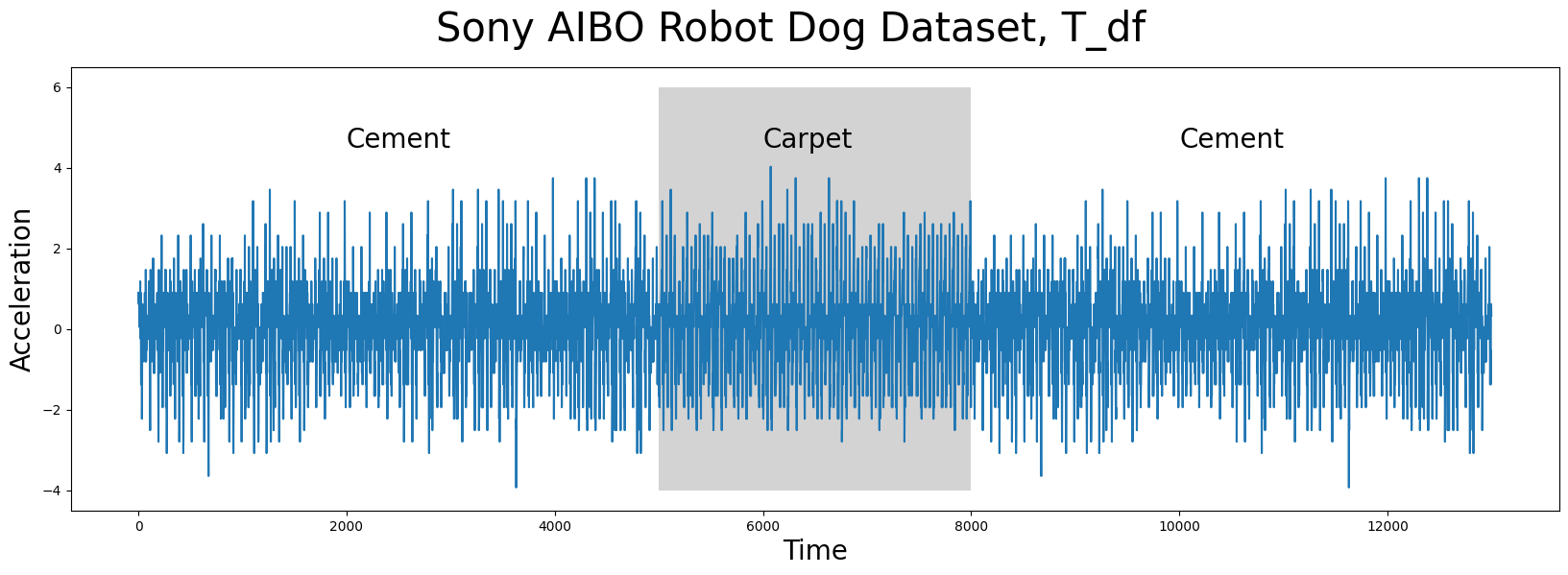
在上面的图中,机器人狗在水泥上行走的时间段以白色背景显示,而机器人狗在地毯上行走的时间段则以灰色背景突出显示。你注意到在不同表面行走之间有明显的差异吗?你能用肉眼观察到任何有趣的见解吗?这个时间序列中是否存在任何保留的模式,如果有,它们在哪里?
你见过这个模式吗?#
我们感兴趣的在时间序列中搜索的子序列模式或查询(如下)看起来是这样的:
Q_df = pd.read_csv("https://zenodo.org/record/4276880/files/carpet_query.csv?download=1")
plt.suptitle('Pattern or Query Subsequence, Q_df', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
plt.plot(Q_df, lw=2, color="C1") # Walking on cement
plt.show()

该模式,Q_df,具有一个窗口长度为m = 100,并且它是从一个完全独立的行走样本中提取的。它看起来有点熟悉吗?在我们之前的时间序列中,有类似的模式存在吗,T_df?你能告诉这个查询样本采集时机器人狗走的表面是什么吗?
为了回答这些问题中的一些,你可以通过计算一种叫做“距离轮廓”的东西,将这个特定的查询子序列或模式与完整的时间序列进行比较。本质上,你将这个单一的查询, Q_df,与 T_df 中的每一个子序列进行比较,方法是计算所有可能的(z标准化的欧几里得)成对距离。因此,距离轮廓只是一个一维向量,它准确地告诉你 Q_df 与 T_df 中找到的每个(相同长度的)子序列有多相似/不相似。现在,计算距离轮廓的一个天真的算法将需要 O(n*m) 的时间来处理,但幸运的是,我们可以做得更好,因为存在一种超高效的方法叫做 “Mueen’s Algorithm for Similarity Search”(MASS),能够以更快的 O(n*log(n)) 时间(log 基数为 2)计算距离轮廓。现在,如果你只有少数短时间序列需要分析,这可能不算什么,但如果你需要多次重复这个过程,并使用不同的查询子序列,那么事情可能会迅速累积。事实上,当时间序列的长度 n 和/或查询子序列的长度 m 变得更长时,天真的算法会花费过多的时间!
使用MASS计算距离轮廓#
所以,给定一个查询子序列, Q_df,和一个时间序列, T_df,我们可以使用 STUMPY 中的 stumpy.mass 函数执行快速相似性搜索并计算距离轮廓:
distance_profile = stumpy.mass(Q_df["Acceleration"], T_df["Acceleration"])
而且,既然 distance_profile 包含了 Q_df 和 T_df 中每个子序列之间的全列表对距离,我们可以通过在 distance_profile 中找到最小距离值并提取其位置索引来检索 T_df 中最相似的子序列:
idx = np.argmin(distance_profile)
print(f"The nearest neighbor to `Q_df` is located at index {idx} in `T_df`")
The nearest neighbor to `Q_df` is located at index 7479 in `T_df`
因此,为了回答我们之前的问题“在我们早期的时间序列 T_df 中是否存在类似的模式?”,让我们继续绘制在 T_df 中最相似的子序列,它位于索引 7479(蓝色),并将其叠加在我们的查询模式 Q_df(橙色)上:
# Since MASS computes z-normalized Euclidean distances, we should z-normalize our subsequences before plotting
Q_z_norm = stumpy.core.z_norm(Q_df.values)
nn_z_norm = stumpy.core.z_norm(T_df.values[idx:idx+len(Q_df)])
plt.suptitle('Comparing The Query To Its Nearest Neighbor', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
plt.plot(Q_z_norm, lw=2, color="C1", label="Query Subsequence, Q_df")
plt.plot(nn_z_norm, lw=2, label="Nearest Neighbor Subsequence From T_df")
plt.legend()
plt.show()

请注意,尽管查询子序列与其最近邻并不完全匹配,STUMPY 仍然能够找到它!然后,为了回答“你能告诉我当这个查询样本被收集时,机器人狗走的是什么表面?”的第二个问题,我们可以准确地查看 idx 在 T_df 中的位置:
plt.suptitle('Sony AIBO Robot Dog Dataset, T_df', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
plt.plot(T_df)
plt.text(2000, 4.5, 'Cement', color="black", fontsize=20)
plt.text(10000, 4.5, 'Cement', color="black", fontsize=20)
ax = plt.gca()
rect = Rectangle((5000, -4), 3000, 10, facecolor='lightgrey')
ax.add_patch(rect)
plt.text(6000, 4.5, 'Carpet', color="black", fontsize=20)
plt.plot(range(idx, idx+len(Q_df)), T_df.values[idx:idx+len(Q_df)], lw=2, label="Nearest Neighbor Subsequence")
plt.legend()
plt.show()
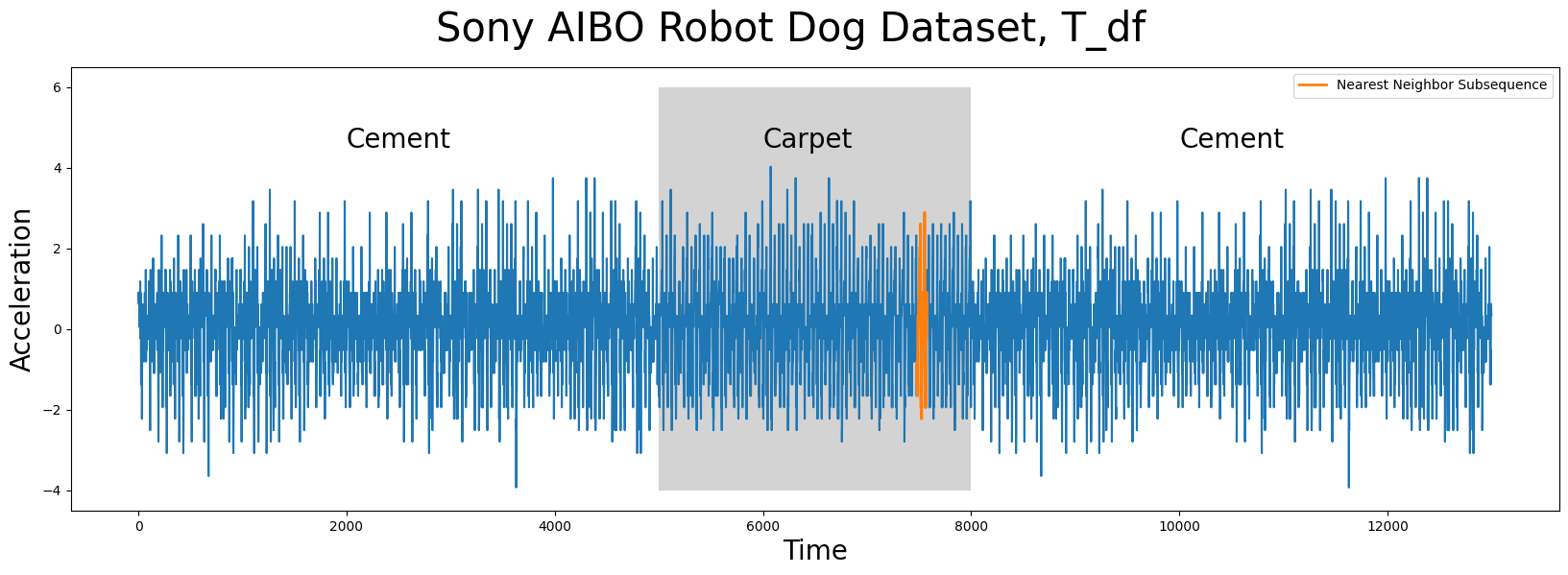
正如我们上面所看到的,离Q_df最近的邻居(橙色)是一个子序列,当机器人狗在地毯上行走时发现的,事实证明,Q_df是从一个独立样本中收集的,该样本也是机器人狗在地毯上行走时收集的!为了进一步说明,我们不仅可以提取最近的邻居,还可以查看前k = 16个最近邻居的位置:
# This simply returns the (sorted) positional indices of the top 16 smallest distances found in the distance_profile
k = 16
idxs = np.argpartition(distance_profile, k)[:k]
idxs = idxs[np.argsort(distance_profile[idxs])]
然后让我们根据它们的索引位置绘制所有这些子序列:
plt.suptitle('Sony AIBO Robot Dog Dataset, T_df', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
plt.plot(T_df)
plt.text(2000, 4.5, 'Cement', color="black", fontsize=20)
plt.text(10000, 4.5, 'Cement', color="black", fontsize=20)
ax = plt.gca()
rect = Rectangle((5000, -4), 3000, 10, facecolor='lightgrey')
ax.add_patch(rect)
plt.text(6000, 4.5, 'Carpet', color="black", fontsize=20)
for idx in idxs:
plt.plot(range(idx, idx+len(Q_df)), T_df.values[idx:idx+len(Q_df)], lw=2)
plt.show()

毫不奇怪,顶部 k = 16 最近邻居的 Q_df(或最佳匹配,以上以多种颜色显示)都可以在机器人狗走在地毯(灰色)时找到!
利用 STUMPY 为您做一些工作#
直到现在,你已经学习了如何使用原始距离轮廓来搜索与你的查询相似的匹配。虽然这可行,但 STUMPY 为你提供了一个超级强大的函数,叫做 stumpy.match,它能为你做更多的工作。使用 stumpy.match 的一个好处是,当它发现每个新邻居时,它会在周围应用一个排除区域,这确保了返回的每个匹配实际上都是你输入查询的唯一出现。在本节中,我们将探讨如何使用它来产生与上述相同的结果。
首先,我们将仅使用两个必需的参数调用 stumpy.match,Q,你的查询,以及 T,你想要搜索的时间序列:
matches = stumpy.match(Q_df["Acceleration"], T_df["Acceleration"])
stumpy.match 返回一个 2D numpy 数组 matches,其中包含所有与 Q 在 T 中的匹配,并按距离排序。第一列表示每个匹配与 Q 的 (z 标准化) 距离,而第二列表示匹配在 T 中的起始索引。如果我们看第一行,我们会看到 Q 在 T 中的最佳匹配从位置 7479 开始,z 标准化距离为 3.955。这正好对应之前的最佳匹配!
现在,您可能会想知道哪些子序列的 T 被认为是 Q 的匹配。之前,我们手动将距离轮廓按升序进行排序,并定义前 16 个匹配为具有最低距离的 16 个子序列。虽然我们可以使用 stumpy.match 模拟此行为(请参见本节末尾),但首选的方法是返回在 T 中所有距离小于某个阈值的子序列。此阈值是通过指定 max_distance 参数来控制的。
STUMPY 尝试找到一个合理的默认值,但通常这非常困难,因为它在很大程度上取决于您特定的数据集和/或领域。例如,如果您拥有一个病人的心电图数据,并且您想匹配一个特定的心跳,那么您可以考虑使用较小的阈值,因为您的时间序列可能非常规律。另一方面,如果您尝试在语音录音中匹配一个特定的单词,那么您可能需要使用较大的阈值,因为您匹配的确切形状可能会受到说话者发音方式的影响。
让我们绘制所有发现的 matches 以查看是否需要调整我们的阈值:
# Since MASS computes z-normalized Euclidean distances, we should z-normalize our subsequences before plotting
Q_z_norm = stumpy.core.z_norm(Q_df.values)
plt.suptitle('Comparing The Query To All Matches (Default max_distance)', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
for match_distance, match_idx in matches:
match_z_norm = stumpy.core.z_norm(T_df.values[match_idx:match_idx+len(Q_df)])
plt.plot(match_z_norm, lw=2)
plt.plot(Q_z_norm, lw=4, color="black", label="Query Subsequence, Q_df")
plt.legend()
plt.show()
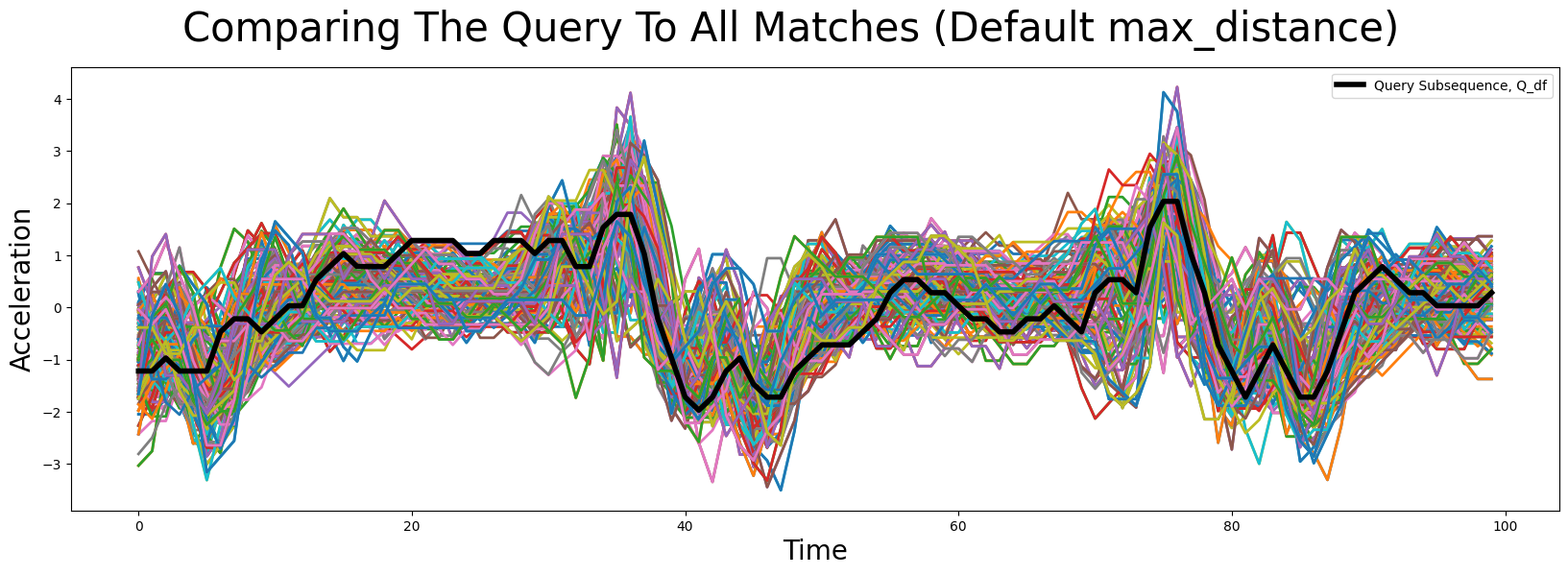
虽然一些主要特征在所有匹配的子序列中有所保留,但似乎还有很多伪影。
使用 stumpy.match,您可以选择两种控制匹配阈值的选项。您可以指定一个常量值(例如,max_distance = 5.0)或提供一个自定义函数。这个函数必须接受一个参数,即距离剖面,D,它是在 Q 和 T 之间计算的。这样,您可以将一些对距离剖面的依赖编码到您的最大距离阈值中。默认的最大距离是 max_distance = max(np.mean(D) - 2 * np.std(D), np.min(D))。这通常是“均值以下两个标准差”。
当然,人们必须稍微实验一下什么是可接受的最大距离,所以让我们尝试将其增加到“低于均值的四个标准差”(即,更小的最大距离)。
matches_improved_max_distance = stumpy.match(
Q_df["Acceleration"],
T_df["Acceleration"],
max_distance=lambda D: max(np.mean(D) - 4 * np.std(D), np.min(D))
)
# Since MASS computes z-normalized Euclidean distances, we should z-normalize our subsequences before plotting
Q_z_norm = stumpy.core.z_norm(Q_df.values)
plt.suptitle('Comparing The Query To All Matches (Improved max_distance)', fontsize='30')
plt.xlabel('Time', fontsize ='20')
plt.ylabel('Acceleration', fontsize='20')
for match_distance, match_idx in matches_improved_max_distance:
match_z_norm = stumpy.core.z_norm(T_df.values[match_idx:match_idx+len(Q_df)])
plt.plot(match_z_norm, lw=2)
plt.plot(Q_z_norm, lw=4, color="black", label="Query Subsequence, Q_df")
plt.legend()
plt.show()
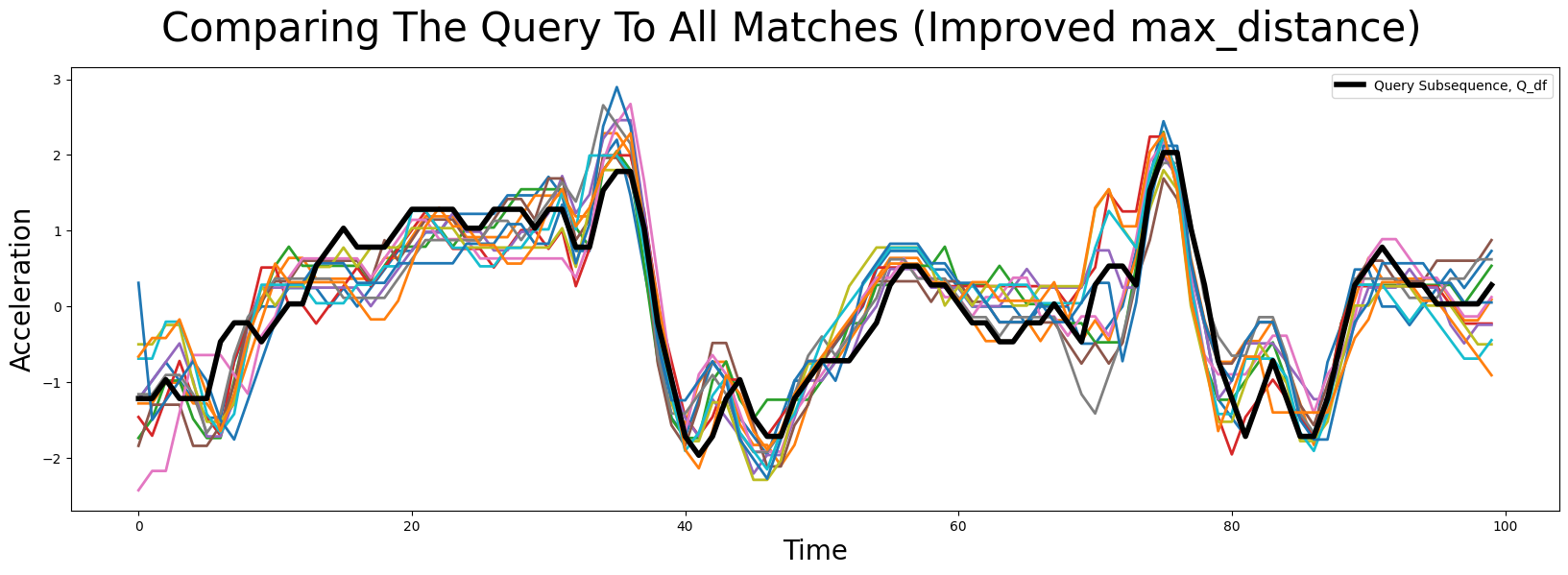
我们看到这看起来更有希望,我们确实找到了非常相似的匹配。有时,有人仍然对指定区域中的所有匹配项不感兴趣。调整此项的最简单方法是将 max_matches 设置为您想要的最大匹配数。默认情况下, max_matches = None,这意味着将返回所有匹配项。
模拟查找所有 Top-k 匹配项#
有时,您可能还没有决定什么是一个好的阈值,因此您可能仍然想找到前k个匹配。在这些情况下,您可能发现需要完全停用默认排除区域,以便找到可能非常接近彼此的匹配(即,接近的索引值)在 T 中。这可以通过将 m / 4(其中 m 是窗口大小)的默认排除区域更改为零来完成。在 STUMPY 中,由于排除区域被计算为 int(np.ceil(m / config.STUMPY_EXCL_ZONE_DENOM)),我们可以通过在计算距离之前显式设置 stumpy.config.STUMPY_EXCL_ZONE_DENOM 来更改排除区域:
m = Q_df["Acceleration"].size
# To set the exclusion zone to zero, set the denominator to np.`inf`
stumpy.config.STUMPY_EXCL_ZONE_DENOM = np.inf
matches_top_16 = stumpy.match(
Q_df["Acceleration"],
T_df["Acceleration"],
max_distance=np.inf, # set the threshold to infinity include all subsequences
max_matches=16, # find the top 16 matches
)
stumpy.config.STUMPY_EXCL_ZONE_DENOM = 4 # Reset the denominator to its default value
为了证明这与我们在教程第一部分所做的相同,我们将断言新找到的索引等于我们使用stumpy.mass方法找到的索引。
npt.assert_equal(matches_top_16[:,1], idxs)
没有错误,这意味着它们确实返回了相同的匹配项!
总结#
就这样!你现在已经使用 STUMPY 的 stumpy.mass 运行了一个已知的兴趣模式(或查询),并能够快速在另一个时间序列中搜索这个模式。此外,你还学会了如何使用 stumpy.match 函数,让 stumpy 为你处理大量的工作。凭借这项新知识,你现在可以去自己的时间序列项目中搜索模式。编码愉快!
附加说明 - 使用非标准化的欧几里得距离的距离轮廓#
有时候,您可能希望使用非标准化的欧几里得距离作为相似性/不相似性的度量,因此您可以通过在调用 stumpy.mass 时简单地设置 normalize=False 来实现。这同样的 normalize=False 参数在以下一组 STUMPY 函数中也可用: stumpy.stump、 stumpy.stumped、 stumpy.gpu_stump 和 stumpy.stumpi。此外, normalize=False 也可以在 stumpy.match 中使用。
附加部分 - 什么使得MASS如此快速?#
MASS比朴素方法快得多的原因是因为MASS使用快速傅里叶变换(FFT)将数据转换到频域,并执行所谓的“卷积”,这将m操作减少到log(n)操作。您可以在原始Matrix Profile I paper中了解更多信息。
这是一个计算距离轮廓的简单实现:
import time
def compute_naive_distance_profile(Q, T):
Q = Q.copy()
T = T.copy()
n = len(T)
m = len(Q)
naive_distance_profile = np.empty(n - m + 1)
start = time.time()
Q = stumpy.core.z_norm(Q)
for i in range(n - m + 1):
naive_distance_profile[i] = np.linalg.norm(Q - stumpy.core.z_norm(T[i:i+m]))
naive_elapsed_time = time.time()-start
print(f"For n = {n} and m = {m}, the naive algorithm takes {np.round(naive_elapsed_time, 2)}s to compute the distance profile")
return naive_distance_profile
对于一个随机时间序列, T_random,具有100万个数据点和一个随机查询子序列, Q_random:
Q_random = np.random.rand(100)
T_random = np.random.rand(1_000_000)
naive_distance_profile = compute_naive_distance_profile(Q_random, T_random)
For n = 1000000 and m = 100, the naive algorithm takes 39.39s to compute the distance profile
朴素算法需要一些时间来计算!然而,MASS 可以在转瞬之间处理这些(甚至更大的数据集):
start = time.time()
mass_distance_profile = stumpy.mass(Q_random, T_random)
mass_elapsed_time = time.time()-start
print(f"For n = {len(T_random)} and m = {len(Q_random)}, the MASS algorithm takes {np.round(mass_elapsed_time, 2)}s to compute the distance profile")
For n = 1000000 and m = 100, the MASS algorithm takes 0.19s to compute the distance profile
为了确保万无一失,让我们确保并检查两种方法的输出是否相同:
npt.assert_almost_equal(naive_distance_profile, mass_distance_profile)
成功,没有错误!这意味着两个输出是相同的。继续尝试吧!
