多维模式发现#
在多维时间序列数据中使用MSTUMP寻找模式#
本教程利用了Matrix Profile VI研究论文中的主要要点,要求使用STUMPY v1.6.1或更高版本。此外,“维度”一词在多维时间序列中是过载的,因为它通常用于指代时间序列的数量和子序列中数据点的数量。为了清晰起见,我们将“维度”的使用限制为仅指时间序列的数量,而不是数据点的数量。
之前,我们介绍了一个概念叫做 时间序列模式,这是在一维时间序列 \(T\) 中发现的保守模式,可以通过计算其 矩阵剖面 使用 STUMPY 来发现。计算一个时间序列的矩阵剖面的过程通常被称为“自连接”,因为时间序列 \(T\) 中的子序列仅与自身进行比较。自从2002年首次引入一维模式发现算法以来,已经进行了大量的努力将模式发现推广到多维情况,但生成多维矩阵剖面是计算上昂贵的,因此必须小心处理以最小化增加的时间复杂性。此外,虽然在所有可用维度中寻找模式可能很诱人(即,一个模式必须存在于所有维度中并同时发生),但已经证明,这样做很少产生有意义的模式,除非是在最复杂的情况下。相反,给定一组时间序列维度,我们应该在将子序列分配为模式之前,将其过滤到一个“有用”维度的子集。例如,看看这个拳击手的动作捕捉,他正在出拳:
from IPython.display import IFrame
IFrame(width="560", height="315", src="https://www.youtube.com/embed/2CQttFf2OhU")
如果我们严格关注拳击手的右臂,在这两种情况下,这两拳几乎是相同的。右肩、右肘和右手的位置(一个三维时间序列)基本上是无法区分的。因此,当我们仅限于所有可用身体运动维度的一个子集时,识别这一击打模式相对简单。然而,如果我们结合来自所有肢体的完整动作捕捉标记(即,将维度数量从三增加),左臂捕捉到的差异以及脚步的细微噪声实际上掩盖了右臂动作的相似性,使得之前的击打模式变得无法找到。这个例子表明经典的多维模式发现算法可能会失败,因为它们试图利用所有可用的维度。因此,我们不仅需要一个有效的算法来计算多维矩阵配置文件,还需要建立一个明智的方法来指导我们选择用于识别多维模式的相关维度子集。
在本教程中,我们将准确解释多维矩阵剖面是什么,然后我们将学习如何使用 mstump 函数(即“多维 STUMP”)通过探索一个简单的玩具数据集来计算它。最后,我们将看看我们是否能够在这个多维时间序列数据中识别出一个有意义的子维度模式(即,仅使用一部分维度)。
开始使用#
让我们导入需要加载、分析和绘制数据的包。
%matplotlib inline
import pandas as pd
import numpy as np
import stumpy
import matplotlib.pyplot as plt
plt.style.use('https://raw.githubusercontent.com/TDAmeritrade/stumpy/main/docs/stumpy.mplstyle')
加载和可视化玩具数据#
在这个示例数据中,我们有一个标记为 T1、T2 和 T3 的三维时间序列。你能找出图案的位置吗?这个图案存在于一个、两个还是全部三个维度中?
df = pd.read_csv("https://zenodo.org/record/4328047/files/toy.csv?download=1")
df.head()
| T1 | T2 | T3 | |
|---|---|---|---|
| 0 | 0.565117 | 0.637180 | 0.741822 |
| 1 | 0.493513 | 0.629415 | 0.739731 |
| 2 | 0.469350 | 0.539220 | 0.718757 |
| 3 | 0.444100 | 0.577670 | 0.730169 |
| 4 | 0.373008 | 0.570180 | 0.752406 |
fig, axs = plt.subplots(df.shape[1], sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Can You Spot The Multi-dimensional Motif?', fontsize='30')
for i in range(df.shape[1]):
axs[i].set_ylabel(f'T{i + 1}', fontsize='20')
axs[i].set_xlabel('Time', fontsize ='20')
axs[i].plot(df[f'T{i + 1}'])
plt.show()
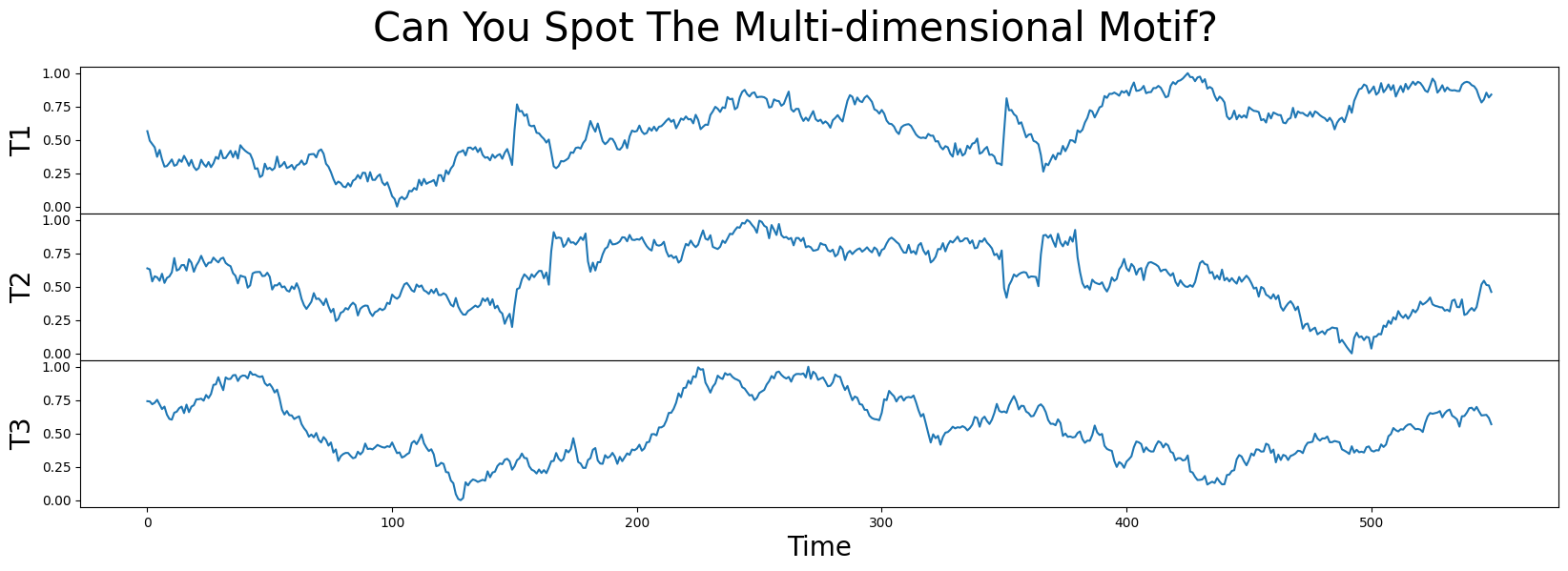
快速的一维探索#
在进行多维矩阵轮廓分析之前,让我们采取一种简单的方法,并在每个维度上独立地运行经典的一维模式发现算法,stumpy.stump(使用窗口大小为m = 30),并提取一维模式对:
m = 30
mps = {} # Store the 1-dimensional matrix profiles
motifs_idx = {} # Store the index locations for each pair of 1-dimensional motifs (i.e., the index location of two smallest matrix profile values within each dimension)
for dim_name in df.columns:
mps[dim_name] = stumpy.stump(df[dim_name], m)
motif_distance = np.round(mps[dim_name][:, 0].astype(float).min(), 1)
print(f"The motif pair matrix profile value in {dim_name} is {motif_distance}")
motifs_idx[dim_name] = np.argsort(mps[dim_name][:, 0])[:2]
The motif pair matrix profile value in T1 is 1.1
The motif pair matrix profile value in T2 is 1.0
The motif pair matrix profile value in T3 is 1.1
当我们再次绘制原始时间序列(如下)以及它们独立发现的模式(粗红线)时,我们可以正确匹配在 T1 和 T2 中视觉上明显的模式对,起始位置接近 150 和 350(虚线垂直线)。请注意,这两个模式的时间并不完美对齐(即,它们并不是同时发生的),但它们彼此相当接近,并且它们的模式对值分别为 1.1 和 1.0。这是一个很好的开始!
fig, axs = plt.subplots(len(mps), sharex=True, gridspec_kw={'hspace': 0})
for i, dim_name in enumerate(list(mps.keys())):
axs[i].set_ylabel(dim_name, fontsize='20')
axs[i].plot(df[dim_name])
axs[i].set_xlabel('Time', fontsize ='20')
for idx in motifs_idx[dim_name]:
axs[i].plot(df[dim_name].iloc[idx:idx+m], c='red', linewidth=4)
axs[i].axvline(x=idx, linestyle="dashed", c='black')
plt.show()

然而,当我们检查 T3 时,它的基序对在位置 50 附近开始重叠(虚线垂直线),并且与在 T1 和 T2 中发现的基序相对较远。哦,不!
事实上,T3 实际上是一个“随机游走”时间序列,它是故意包含在这一组中的诱饵,并且与 T1 和 T2 不同,T3 完全不包含任何保守的行为,尽管它的特征对之间的距离是 1.1,这是一个红鲱鱼。这表明了几个重要的观点:
如果存在额外的不相关维度(即,
T3),如果你不忽视/否定那些干扰维度,你在发现多维模式方面的表现大致与随机机会相当如果你怀疑只有一部分时间序列中存在模式,你如何知道哪些维度相关,或者你甚至如何知道有多少维度是相关的?
在所有维度上进行模体搜索几乎总是保证会产生毫无意义的结果,即使某些维度具有明确而清晰的模体(就像我们上面的例子)
对文献中所有当前多维模式发现算法的快速调查(见Matrix Profile VI中的第二节)显示,它们速度慢、近似、并且对不相关维度脆弱。相比之下,我们需要的是一个快速、精确并且对数百个不相关维度和虚假数据鲁棒的算法。这就是stumpy.mstump可以提供帮助的地方!
多维矩阵剖面#
在Matrix Profile VI论文中提供的多维矩阵剖面的定义是无可替代的(见第III节和第IV节),因此我们建议读者参考这个基础资源以获得详细的信息。不过,为了培养一些基本的直觉,我们将分享一个用于计算多维矩阵剖面的过于简单化的描述,但请知道,stumpy.mstump函数提供了一个高效、准确且可扩展的变体,以替代这里提供的幼稚解释。
首先,我们必须从消除一个关于多维矩阵轮廓的常见误解开始:
多维矩阵剖面不是一个个堆叠在一起的一维矩阵剖面!
那么,多维矩阵剖面是什么?要回答这个问题,让我们暂时离开我们的玩具数据示例,假设我们有一个“多维时间序列”,\(T = [T1, T2, T3, T4]\),它具有\(d = 4\)个维度和长度\(n = 7\)(即,每个维度内有七个数据点或“位置”)。然后,\(T\)的形状简单为\(d\times n\)(或\(4\times 7\))。如果我们选择窗口大小\(m = 3\),那么我们可以将\(i^{th}\)“多维子序列”定义为从位置\(i\)开始的长度为\(m\)的\(T\)中值的连续子集,其整体形状为\(d\times m\)(或\(4\times 3\))。你可以将每个多维子序列视为\(T\)的一个矩形切片,并且\(T\)只能有恰好\(l = n - m + 1\)个多维子序列。在我们的示例中,\(T\)恰好有\(l = 5\)个多维子序列(即,我们只能在\(T\)的长度上滑动一个\(4\times 3\)形状的矩形\(5\)次,直到到达\(T\)的末尾),对于\(i^{th}\)个多维子序列,我们可以独立遍历其每个维度,并计算一个聚合的“多维距离剖面”(即,四个1-dimensional distance profiles叠在一起)。本质上,\(i^{th}\)个多维距离剖面的形状为\(d\times l\)(或\(4\times 5\)),它为你提供了\(i^{th}\)个多维子序列与\(T\)中所有其他可能的多维子序列之间的成对距离。
请记住,我们的最终目标是输出一种称为“多维矩阵轮廓”(及其相应的“多维矩阵轮廓索引”)的东西,其整体形状为 \(d\times l\)(即,每个 \(l\) 多维子序列对应一组 \(d\) 值)。事实证明,多维矩阵轮廓的 \(i^{th}\) 列中的值直接来源于 \(i^{th}\) 多维距离轮廓。继续我们的例子,我们来用下面的虚构数组来表示 \(i^{th}\) 多维子序列的典型多维距离轮廓,来说明这个过程:
ith_distance_profile = np.ndarray([[0.4, 0.2, 0.6, 0.5, 0.2, 0.1, 0.9],
[0.7, 0.0, 0.2, 0.6, 0.1, 0.2, 0.9],
[0.6, 0.7, 0.1, 0.5, 0.8, 0.3, 0.4],
[0.7, 0.4, 0.3, 0.1, 0.2, 0.1, 0.7]])
通过这个,我们现在可以识别出形成多维矩阵轮廓第 \(i^{th}\) 列向量的 \(d\) 值集合,该矩阵的形状为 \(d\times 1\)(或 \(4\times 1\))。第一个维度的值通过提取 ith_distance_profile 每列中的最小值找到,然后返回缩减集合中的最小值。然后,第二个维度的值通过提取 ith_distance_profile 每列中的两个最小值,计算这两个值的平均值,然后返回缩减集合中的最小平均值找到。最后,第 \(k^{th}\) 个维度的值通过提取 ith_distance_profile 每列中的 \(k\) 个最小值,计算这 \(k\) 个值的平均值,然后返回缩减集合中的最小平均值找到。一个简单的算法可能看起来像这样:
ith_matrix_profile = np.full(d, np.inf)
ith_indices = np.full(d, -1, dtype=np.int64)
for k in range(1, d + 1):
smallest_k = np.partition(ith_distance_profile, k, axis=0)[:k] # retrieves the smallest k values in each column
averaged_smallest_k = smallest_k.mean(axis=0)
min_val = averaged_smallest_k.min()
if min_val < ith_matrix_profile[k - 1]:
ith_matrix_profile[k - 1] = min_val
ith_indices[k - 1] = averaged_smallest_k.argmin()
因此,只需沿着 \(T\) 的整个长度推进 \(i^{th}\) 多维子序列,然后计算其对应的 \(i^{th}\) 多维矩阵轮廓(及其索引),我们就可以轻松填充完整的多维矩阵轮廓和多维矩阵轮廓索引。希望你能同意我们的初始声明:
多维矩阵轮廓不是一个个堆叠在一起的一维矩阵轮廓!
那么,多个维度的矩阵轮廓的每个维度究竟告诉我们什么呢?本质上,多个维度的矩阵轮廓的\(k^{th}\)维度(或行)存储每个子序列与其最近邻之间的距离(这个距离是通过我们上面看到的\(k\)维度距离函数计算得出的)。我们应该指出,针对多个维度的矩阵轮廓的\(k^{th}\)维度,仅选择了一部分时间序列维度(即从\(d\)个维度中选择\(k\)个),而这个选择的维度子集可以随着您改变\(i^{th}\)多个维度的子序列和/或\(k\)而变化。
现在我们更好地理解了什么是多维矩阵轮廓,接下来我们只需在我们的原始玩具数据集上调用 stumpy.mstump 函数来计算它:
mps, indices = stumpy.mstump(df, m)
因此,“\(k\)维图样”可以通过定位对应的\(k\)维矩阵剖面的最低值来找到,mps:
motifs_idx = np.argmin(mps, axis=1)
并且“\(k\)维最近邻”的索引位置可以通过以下方式找到:
nn_idx = indices[np.arange(len(motifs_idx)), motifs_idx]
最后,我们可以绘制所有可能的 \(k\) 维矩阵概况(橙色线)和原始时间序列数据(蓝色线):
fig, axs = plt.subplots(mps.shape[0] * 2, sharex=True, gridspec_kw={'hspace': 0})
for k, dim_name in enumerate(df.columns):
axs[k].set_ylabel(dim_name, fontsize='20')
axs[k].plot(df[dim_name])
axs[k].set_xlabel('Time', fontsize ='20')
axs[k + mps.shape[0]].set_ylabel(dim_name.replace('T', 'P'), fontsize='20')
axs[k + mps.shape[0]].plot(mps[k], c='orange')
axs[k + mps.shape[0]].set_xlabel('Time', fontsize ='20')
axs[k].axvline(x=motifs_idx[1], linestyle="dashed", c='black')
axs[k].axvline(x=nn_idx[1], linestyle="dashed", c='black')
axs[k + mps.shape[0]].axvline(x=motifs_idx[1], linestyle="dashed", c='black')
axs[k + mps.shape[0]].axvline(x=nn_idx[1], linestyle="dashed", c='black')
if dim_name != 'T3':
axs[k].plot(range(motifs_idx[k], motifs_idx[k] + m), df[dim_name].iloc[motifs_idx[k] : motifs_idx[k] + m], c='red', linewidth=4)
axs[k].plot(range(nn_idx[k], nn_idx[k] + m), df[dim_name].iloc[nn_idx[k] : nn_idx[k] + m], c='red', linewidth=4)
axs[k + mps.shape[0]].plot(motifs_idx[k], mps[k, motifs_idx[k]] + 1, marker="v", markersize=10, color='red')
axs[k + mps.shape[0]].plot(nn_idx[k], mps[k, nn_idx[k]] + 1, marker="v", markersize=10, color='red')
else:
axs[k + mps.shape[0]].plot(motifs_idx[k], mps[k, motifs_idx[k]] + 1, marker="v", markersize=10, color='black')
axs[k + mps.shape[0]].plot(nn_idx[k], mps[k, nn_idx[k]] + 1, marker="v", markersize=10, color='black')
plt.show()

请注意,(植入的) 有语义的图案(厚重的红线)可以通过检查最低点的位置(红色箭头)在 P1 或 P2 矩阵轮廓中可视化地找到,但 P3 的情况在一个有效随机的位置识别了图案(黑色箭头),这进一步强化了我们之前提出的观点:
如果存在额外的不相关维度(即,
T3),如果你不忽视/否定那些干扰维度,你在发现多维模式方面的表现大致与随机机会相当
此外,这可能看起来违反直觉,但正如上面所示,较低维度的模式可能不是更高维度模式的一个子集,因为较低维度的模式对可能比更高维度模式对中的任何维度子集更接近。一般来说,这是一个微妙但重要的观点,需要牢记。
寻找 \(k\) - 天真的方法#
那么我们如何选择“合适的” \(k\) 呢?一种简单的方法是将此转化为一个经典的肘部/膝盖寻找问题,通过绘制每个维度中最小矩阵轮廓值与 \(k\) 的关系,然后寻找“转折点”(即最大曲率点):
plt.plot(mps[range(mps.shape[0]), motifs_idx], c='red', linewidth='4')
plt.xlabel('k (zero-based)', fontsize='20')
plt.ylabel('Matrix Profile Value', fontsize='20')
plt.xticks(range(mps.shape[0]))
plt.plot(1, 1.3, marker="v", markersize=10, color='red')
plt.show()
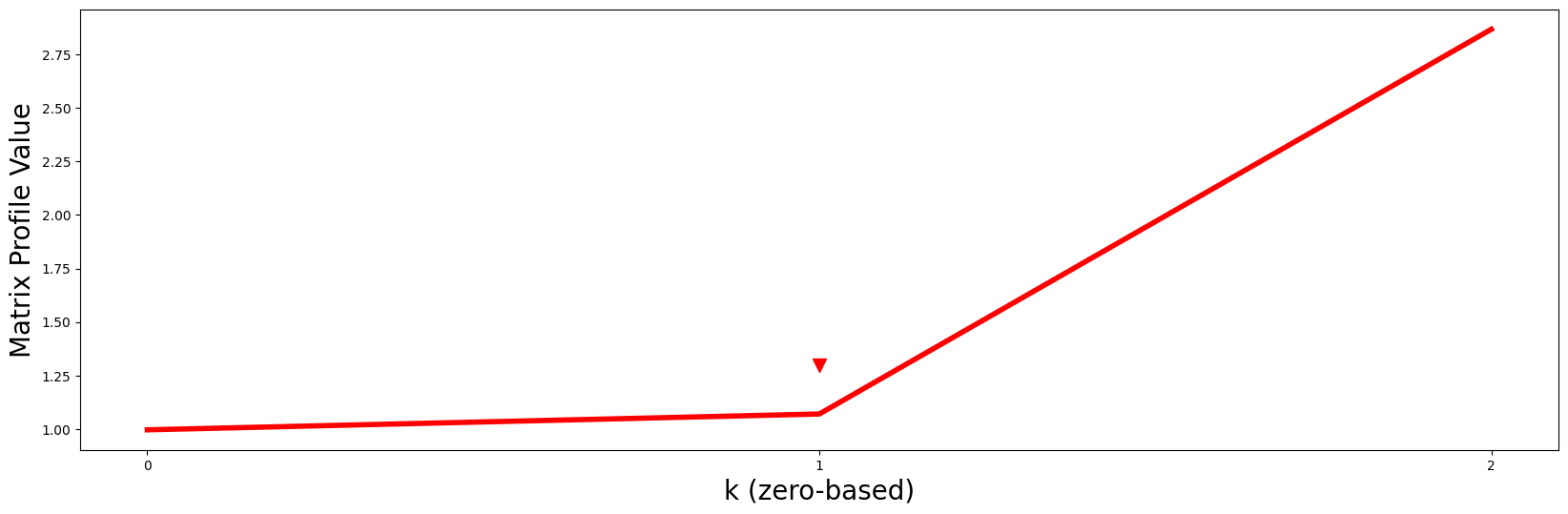
请注意,在\(k = 1\)(红色箭头)之后,红线急剧向上弯曲,就像一个“曲棍球棒”,因此,自然地,我们应该选择\(P2\)及其图案作为所有可能的\(k\)维图案中最好的图案。
寻找 \(k\) - 最小描述长度方法#
不幸的是,上述简单的肘部查找方法并不稳健,无法轻易自动化,因此Matrix Profile VI论文的作者建议计算一种叫做“最小描述长度”(MDL)的东西,这是一种花哨的说法,意思是:“对于给定的动机对,如果您只能使用\(k\)维度中的一个来自多维子序列来压缩其最近邻的\(k\)维子序列,那么结果压缩大小是多少?” 换句话说,\(k\)维动机对有多相似?当我们通过利用MDL来回答这个问题时,我们会发现,高相似度的\(k\)维动机对将允许最大的信息/数据压缩,位数或“位大小”通常会低于同类同伴。因此,如果我们使用MDL框架为给定动机对计算每个k维度的位大小,那么我们需要做的就是寻找全局最小值。对于我们的例子,让我们使用stumpy.mdl计算MDL:
mdls, subspaces = stumpy.mdl(df, m, motifs_idx, nn_idx)
这里, mdls 包含每个 \(k\) 的位数,而 subspaces 是一个列表,确切告诉你用于计算第 \(k\) 个 MDL 值的所有维度的哪一个子集。现在,让我们可视化 MDL 结果:
plt.plot(np.arange(len(mdls)), mdls, c='red', linewidth='4')
plt.xlabel('k (zero-based)', fontsize='20')
plt.ylabel('Bit Size', fontsize='20')
plt.xticks(range(mps.shape[0]))
plt.plot(1, 1520, marker="v", markersize=10, color='red')
plt.show()
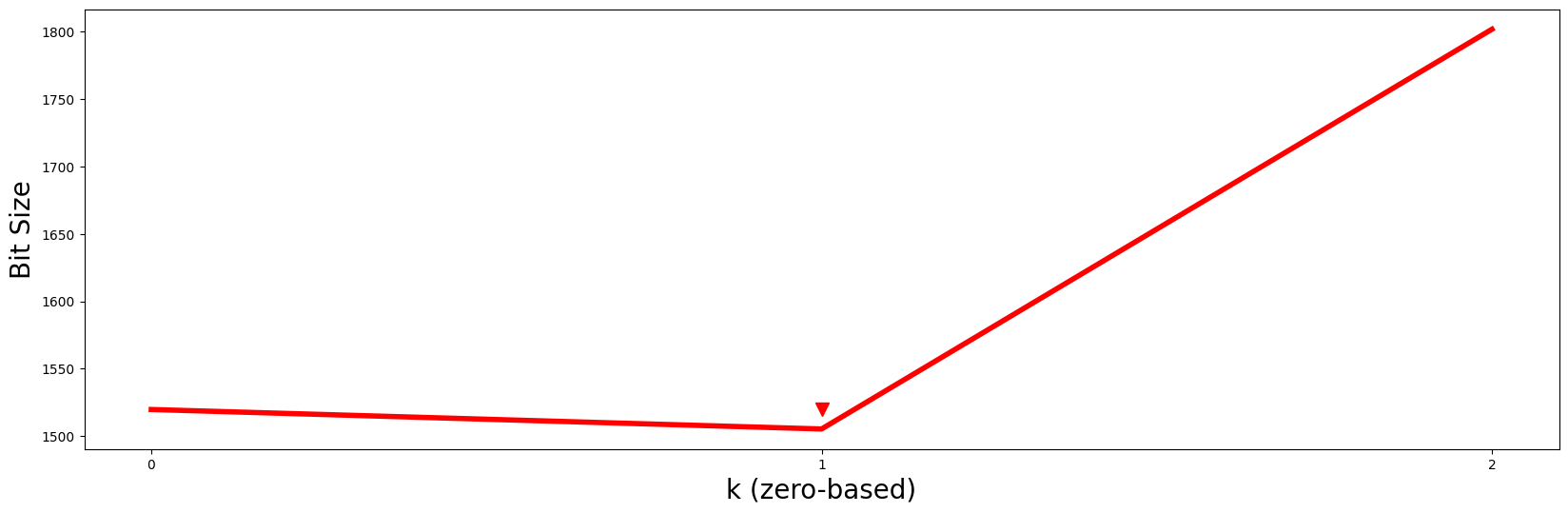
本质上,通过寻找最小位数的 \(k\) 的值,我们应该选择 \(P2\) 及其模式作为所有可能的 \(k\) 维模式中的最佳模式。此外,为这个 \(k = 1\) 模式选择的维度子集(即,subspaces[k])可以从 subspaces 中轻松检索:
k = np.argmin(mdls)
print(df.columns[subspaces[k]])
Index(['T2', 'T1'], dtype='object')
因此,符合我们上述讨论的内容,列 T2 和 T1 包含了最佳的模式!为了更加明确这一点,让我们为我们的玩具数据集添加更多的随机游走诱饵,随机打乱列的顺序,并再次比较最小的 \(k\)-维矩阵轮廓值:
for i in range(4, 11):
df[f'T{i}'] = np.random.uniform(0.1, -0.1, size=df.shape[0]).cumsum()
df = df.sample(frac=1, axis="columns") # Randomly shuffle the columns
fig, axs = plt.subplots(df.shape[1], sharex=True, gridspec_kw={'hspace': 0})
plt.suptitle('Can You Still Spot The Multi-dimensional Motif?', fontsize='30')
for i, colname in enumerate(df.columns):
axs[i].set_ylabel(colname, fontsize='20')
axs[i].set_xlabel('Time', fontsize ='20')
axs[i].plot(df[colname])
plt.show()
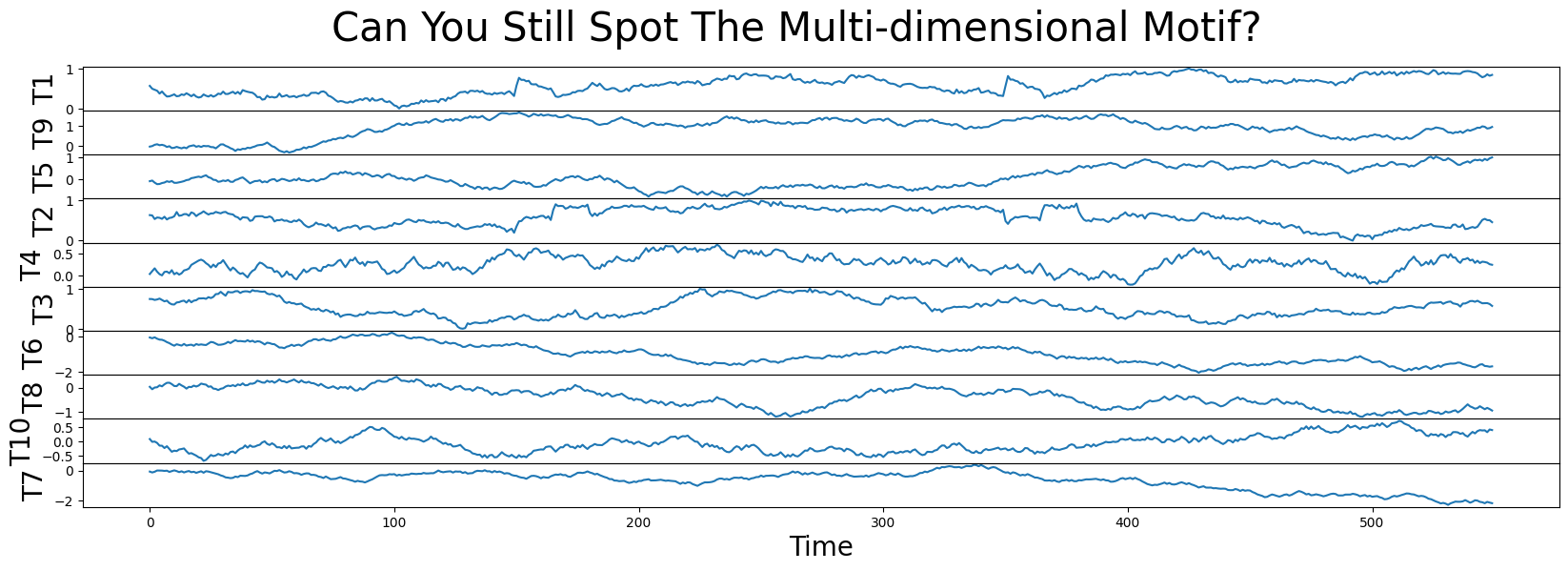
mps, indices = stumpy.mstump(df, m)
motifs_idx = np.argmin(mps, axis=1)
nn_idx = indices[np.arange(len(motifs_idx)), motifs_idx]
mdls, subspaces = stumpy.mdl(df, m, motifs_idx, nn_idx)
k = np.argmin(mdls)
plt.plot(np.arange(len(mdls)), mdls, c='red', linewidth='4')
plt.xlabel('k (zero-based)', fontsize='20')
plt.ylabel('Bit Size', fontsize='20')
plt.xticks(range(mps.shape[0]))
plt.plot(k, 1.01 * mdls[k], marker="v", markersize=10, color='red')
plt.show()
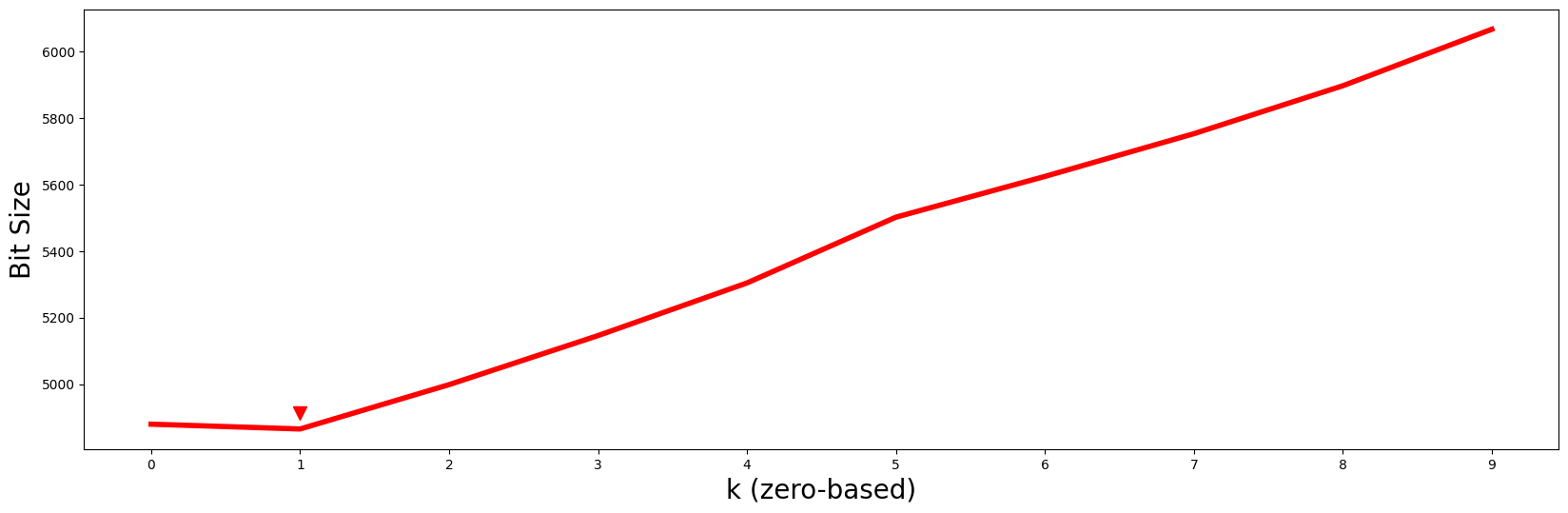
即使增加了7个额外的诱饵,最小的MDL位大小仍然发生在 \(k = 1\) (红色箭头)处,因此我们应该继续选择 \(P2\) 及其motif作为所有可能的 \(k\) 维motif中最好的motif。再说一次,尽管我们的数据列已经被随机打乱,但相应的子空间仍然可以通过以下方式轻松检索:
k = np.argmin(mdls)
print(df.columns[subspaces[k]])
Index(['T2', 'T1'], dtype='object')
矩阵剖面子空间#
有时您可能会发现需要计算(单一的)“\(k\)维矩阵剖面子空间”,而无需计算MDL(例如,如果您由于某些先前知识或约束而已经心中有一个特定的\(k\)值)。幸运的是,STUMPY便捷函数,stumpy.subspace,可以帮助我们!
要使用 stumpy.subspace,我们只需传入:
用于计算多维矩阵剖面的多维时间序列,
df窗口大小,
m,用于计算多维矩阵剖面第 \(k^{th}\) 维度的模式对的索引,
motifs_idx[k]和nn_idx[k](来自indices[np.arange(len(motifs_idx)), motifs_idx[k]])期望的(零为基础)维度,
k
k = 1
subspace = stumpy.subspace(df, m, motifs_idx[k], nn_idx[k], k)
print(f"For k = {k}, the {k + 1}-dimensional subspace includes subsequences from {df.columns[subspace].values}")
For k = 1, the 2-dimensional subspace includes subsequences from ['T2' 'T1']
所以,在使用 mstump 计算多维矩阵概况并选择第二个维度(即,\(k = 1\))后,根据 \(k\) 维子空间,应该从所有可能的时间序列维度中提取 T2 和 T1 的模式。
奖金部分#
MSTUMPED - 分布式 MSTUMP#
根据维度总数和时间序列数据的长度,生成多维矩阵剖面可能计算开销较大。因此,您可以通过尝试 mstumped 来克服这一点,这是一个基于 Dask distributed 的 mstump 的分布式和并行实现。
import stumpy
from dask.distributed import Client
if __name__ == "__main__":
with Client() as dask_client:
mps, indices = stumpy.mstumped(dask_client, df, m) # Note that a dask client is needed
受限搜索#
可能会有一些情况,您希望在\(k\)维度上寻找最佳模式,但您希望明确“包括”或“排除”一组特定的维度。在简单的排除情况下,只需在调用mstump之前省略不需要的时间序列维度:
mps, indices = stumpy.mstump(df[df.columns.difference(['T3'])], m) # This excludes the `T3` dimension
然而,在包含的情况下,用户可能有特定的时间序列维度,他们总是希望在多维矩阵特征输出中包含或优先考虑,因此您可以提供一个(零基)维度的列表作为参数:
mps, indices = stumpy.mstump(df, m, include=[0, 1])
motifs_idx = np.argmin(mps, axis=1)
nn_idx = indices[np.arange(len(motifs_idx)), motifs_idx)
因此,在这个例子中,我们指示 mstump include=[0, 1](即 T1 和 T2),当 \(k\ge 1\) 时,\(k^{th}\) 维矩阵配置子空间:
k = 2
S = stumpy.subspace(df, m, motifs_idx[k], nn_idx[k], k, include=[0, 1])
将始终包括 T1 和 T2。类似地,\(k\lt 1\) 将包括 T1 或 T2。
警告
当您使用include参数指定在计算多维矩阵概要时要包含哪些时间序列维度时,您生成了一个“特定于包含”的多维矩阵概要,因此,您必须记得在其他也接受include参数的互补函数中设置相同的include参数。换句话说,如果您使用include生成一个“特定于包含”的多维矩阵概要来搜索样式,而您忘记在例如stumpy.mdl、stumpy.subspace或stumpy.mmotifs中也设置相同的include参数,那么您的结果可能完全错误/无意义。在使用include参数时必须格外小心。
最后,除了搜索模式之外,还可以让 mstump 通过简单地传递 discords=True 参数来搜索异常:
mps, indices = stumpy.mstump(df, m, discords=True)
discords_idx = np.argmax(mps, axis=1)
nn_idx = indices[np.arange(len(discords_idx)), discords_idx)
k = 2
S = stumpy.subspace(df, m, discords_idx[k], nn_idx[k], k, discords=True)
此函数返回的是在\(k\)个维度中最大的平均距离,而不是返回最小的平均距离。然而,请注意我们使用np.argmax来专注于异常值。返回异常值的能力是STUMPY的独特之处,并未在原始论文中发表。
警告
当您使用 discord=True 计算多维矩阵轮廓时,您生成了一个“特定于异常”的多维矩阵轮廓,因此,您必须在所有地方设置 discords=True。换句话说,您不能使用这个“特定于异常”的多维矩阵轮廓来搜索模式。相反,您必须重新计算一个“特定于模式”的多维矩阵轮廓(即,通过在所有地方设置 discords=False)。在使用 discords 参数时必须格外小心。
还要注意,可以同时包含特定维度并搜索不和谐之处:
mps, indices = stumpy.mstump(df, m, include=[0, 1], discords=True)
discords_idx = np.argmax(mps, axis=1)
nn_idx = indices[np.arange(len(discords_idx)), discords_idx)
k = 2
S = stumpy.subspace(df, m, discords_idx[k], nn_idx[k], k, include=[0, 1], discords=True)
在这种情况下,在 include 中列出的维度优先得到尊重,然后所有后续维度按它们在 \(k\) 维度上的最大平均距离进行排序。
总结#
就这样!您刚刚学习了如何使用 stumpy.mstump (或 stumpy.mstumped)分析多维时间序列数据的基础知识。祝编码愉快!
