具有多个昂贵治疗臂的Qini曲线

本笔记本展示了使用maq包中提供的多臂Qini指标（可在https://github.com/grf-labs/maq获取）来评估来自causalML的多臂CATE估计器的方法。

该指标是将熟悉的Qini曲线推广到我们拥有多个处理臂的设置中，并且根据某些已知的成本结构，分配处理的成本可能因单位和处理臂而异。从高层次来看，该指标基本上允许您通过进行成本效益分析来量化使用更多处理臂进行定向的价值，该分析使用您的CATE估计值在各种预算约束下将处理臂分配给最具成本效益的单位。

本笔记本简要概述了统计设置，并通过一个简单的模拟示例进行了演练。

要使用此功能，您首先需要从GitHub安装maq Python包。可以使用以下命令安装最新的源代码版本：

pip install "git+https://github.com/grf-labs/maq.git#egg=maq&subdirectory=python-package"

# Treatment effect estimators (R-learner with Causal ML + XGBoost)
from causalml.inference.meta import BaseRRegressor
from xgboost import XGBRFRegressor

# Generalized Qini curves
from maq import MAQ, get_ipw_scores

import numpy as np
np.random.seed(42)

统计设置

让 \(k = 1, \ldots K\) 表示 \(K\) 个互斥且成本高昂的治疗组之一，\(k = 0\) 表示一个（无成本的）对照组。让 \(Y_i(k)\) 表示单位 i 在第 \(k\) 组的潜在结果，\(X_i\) 表示一组可观察的特征。

让函数 \(\hat \tau(\cdot)\) 成为从训练集中获得的条件平均处理效应（CATE）的估计，其中第 \(k\) 个元素估计

\[\tau_k(X_i) = E[Y_i(k) - Y(0) ~|~ X_i].\]

Qini曲线\(Q(B)\)量化了根据我们的估计函数\(\hat \tau(\cdot)\)在不同预算约束\(B\)下分配治疗的价值。在单一治疗组\(K=1\)的情况下，我们可以将其形式化为

\[Q(B) = E[ \pi_B(X_i)\left( Y_i(1) - Y_i(0) )\right] = E[\pi_B(X_i) \tau(X_i)],\]

其中 \(\pi_B(X_i) \in \{0, 1\}\) 是策略，它将治疗（=1）分配给那些由 \(\hat \tau(\cdot)\) 预测为受益最多的单位，这样我们平均承担的成本最多为 B。如果我们让 \(C(\cdot)\) 表示我们已知的成本函数（例如，\(C(X_i) = 4.2\) 表示在某个选择的成本单位下，分配给第 \(i\) 个单位的治疗成本为 4.2），那么 \(\pi_B\) 将如下所示

\[\pi_B = argmax_{\pi} \left\{ E[\pi_B(X_i) \hat \tau(X_i)] : E[\pi_B(X_i) C(X_i)] \leq B \right\}\]

虽然正式写下来有点令人生畏，但事实证明表达\(\pi_B\)非常简单：它基本上归结为一个阈值规则：对于给定的\(B\)，处理那些预测的成本效益比\(\frac{\hat \tau(X_i)}{C(X_i)}\)高于截止值的单位。Qini曲线可以用来量化价值，通过使用估计函数\(\hat \tau(\cdot)\)和成本结构\(C(\cdot)\)来分配治疗时，与为每个单位分配控制臂相比的预期增益来衡量，随着我们改变可用预算\(B\)。

在多个治疗组 \(K > 1\)的情况下，我们感兴趣的对象，即Qini曲线，是相同的，我们只需要在符号中添加一个内积 \(\langle,\rangle\)

\[Q(B) = E[\langle \pi_B(X_i),~ \tau(X_i) \rangle],\]

表示\(\pi_B(X_i)\)现在是一个\(K\)长度的选择向量，如果我们在给定的预算约束下预测将第\(i\)个单位分配到该臂是最优的，则在第\(k\)个条目中为1。与上面类似，\(\pi_B\)采用以下形式

\[\pi_B = argmax_{\pi} \left\{ E[\langle \pi_B(X_i),~ \hat \tau(X_i)\rangle] : E[\langle \pi_B(X_i),~ C(X_i)\rangle] \leq B \right\}.\]

表达 \(\pi_B\) 现在变得更加复杂，因为对于每个预算约束 \(B\)，\(\pi_B\) 必须做出类似“我应该为第 \(i\) 个单位分配初始臂，或者如果第 \(j\) 个单位已经被分配了一个臂：我应该将这个人升级到一个更昂贵但更有效的臂吗？”的决策。事实证明，可以将 \(\pi_B\) 表达为阈值规则（详情请参阅这篇 论文），从而为多臂治疗规则构建Qini曲线提供了可行的方法。

示例

在训练集上拟合CATE函数

生成一些简单的（合成的）数据，其中\(K=2\)个治疗组，第二个组在平均上更有效。

n = 20000
p = 5

# Draw a treatment assignment from {0, 1, 2} uniformly
W = np.random.choice([0, 1, 2], n)
# Generate p observable characteristics where some are related to the CATE
X = np.random.rand(n, p)
Y = X[:, 1] + X[:, 2]*(W == 1) + 1.5*X[:, 3]*(W == 2) + np.random.randn(n)
# (in this example, the true arm 2 CATE is 1.5*X[:, 3])

# Generate a train/test split
n_train = 15000
ix = np.random.permutation(n)
train, test = ix[:n_train], ix[n_train:]

通过在训练集上拟合一个CATE估计器（例如使用R-learner）来获得\(\hat \tau(\cdot)\)。

# Use known propensities (1/3)
W_hat = np.repeat(1 / 3, n_train)
propensities = {0: W_hat, 1: W_hat, 2: W_hat}

tau_function = BaseRRegressor(XGBRFRegressor(), random_state=42)
tau_function.fit(X[train, :], W[train], Y[train], propensities)

在测试集上估计Q(B)

在高层面上，估计Qini曲线\(Q(B)\)涉及两个任务。第一个是估计基础策略\(\pi_B\)，第二个是估计该策略的价值。

正如前一节所述，由于存在多个昂贵的治疗臂，策略\(\pi_B\)的计算比单臂情况更为复杂，因为给定一个治疗效果函数（从某个训练集获得）和一个成本结构，我们需要在每个预算约束下确定将哪个臂分配给哪个单元。maq包通过一个算法执行这个第一步，该算法给出了多臂策略\(\pi_B\)的路径。

在估计此政策价值的第二步中，我们需要构建一个合适的评估分数矩阵（我们用\(\Gamma\)表示），这些分数具有在平均时作为处理效果估计的特性。

如果我们知道治疗随机化概率 \(P[W_i=k~|~X_i]\)，那么构建这些分数就变得容易了：我们可以简单地使用逆概率加权（IPW）。对于 \(K\) 个治疗组，第 \(k\) 组的分数采用以下形式

\[\Gamma_{i,k} = \frac{1(W_i=k)Y_i}{P[W_i=k~|~X_i]} - \frac{1(W_i=0)Y_i}{P[W_i=0~|~X_i]},\]

其中 \(W_i\) 和 \(Y_i\) 是测试集单元 i 的处理分配和观察结果。第 \(k\) 个臂的 ATE 估计由这些分数的平均值给出：\(\frac{1}{n_{test}} \sum_{i=1}^{n_{test}} \Gamma_{i,k}\)。基于 IPW 的 \(Q(B)\) 估计将是这些分数的平均值，这些分数“匹配”基础政策处方 \(\pi_B\)。

maq 包有一个简单的便利工具 get_ipw_scores，可以通过 IPW 来构建这些（默认情况下假设臂具有均匀分配概率 \(\frac{1}{K+1}\)）。

注意：如果随机化概率未知（如在观察性研究中可能发生的情况），则可以通过将倾向得分的估计值代入上述表达式来形成得分，这是一种更稳健的替代方法，即使用增强逆倾向加权（AIPW），从而获得Qini曲线的双重稳健估计。此处不涵盖此方法，详情请参阅论文。

# Construct an n_test*K matrix of evaluation scores
IPW_scores = get_ipw_scores(Y[test], W[test])

# Predict CATEs on the test set
tau_hat = tau_function.predict(X[test, :])

# Specify our cost structure,
# assume the cost of assigning each unit the first arm is 0.2
# and the cost of assigning each unit the second more effective arm is 0.5
# (these can also be array-valued if costs vary by unit)
cost = [0.2, 0.5]

# Start by fitting a baseline Qini curve that only considers the average treatment effects and costs
qini_baseline = MAQ(target_with_covariates=False, n_bootstrap=200)
qini_baseline.fit(tau_hat, cost, IPW_scores)

qini_baseline.plot()

这条曲线在\(B=0.2\)处有一个拐点：第一段描绘了低成本臂的平均处理效应（ATE），第二段描绘了成本较高但平均效果更好的臂的平均处理效应。曲线上的点表示针对任意一组单位时的平均单位效益。

例如，在平均支出为0.2时，我们的收益（以及标准误差）等于臂1的平均处理效应（ATE）

qini_baseline.average_gain(0.2)

(0.49665725358631685, 0.047913821952266705)

接下来，我们为臂1拟合一个Qini曲线

tau_hat_1 = tau_hat[:, 0]
cost_1 = cost[0]
IPW_scores_1 = IPW_scores[:, 0]

qini_1 = MAQ(n_bootstrap=200).fit(tau_hat_1, cost_1, IPW_scores_1)

qini_baseline.plot(show_ci=False)
# Plot curve with 95% confidence bars
qini_1.plot(color="blue", label="arm 1")

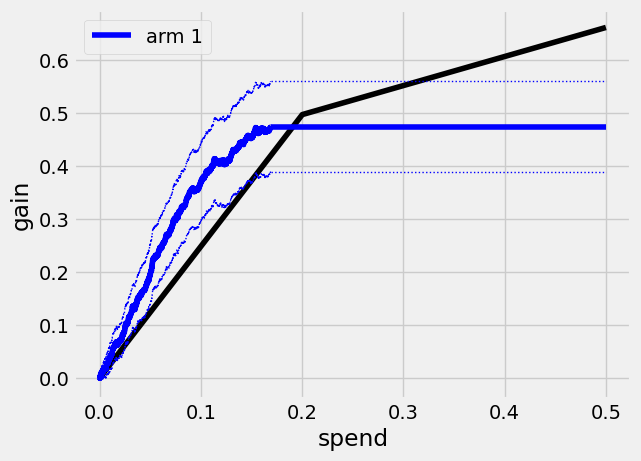
这个臂的Qini曲线在花费大约

print(qini_1.path_spend_[-1])

0.168840000000009

这意味着在这个支出水平上，我们已经对所有预测会从治疗中受益的单位进行了治疗（即tau_hat_1大于0）。我们可以从曲线上读取估计值和标准误差，例如在每单位支出\(B=0.1\)时，每单位的估计平均治疗效果是

qini_1.average_gain(0.1)

(0.36935574662263526, 0.037401976389534526)

（这些标准误差是基于估计函数 \(\hat \tau(\cdot)\) 的，并量化了在估计Qini曲线时测试集的不确定性）。

我们可以通过估计蓝线和黑线之间的垂直差异来评估在不同支出水平下使用臂1进行定向的价值。让我们将臂1的Qini曲线称为\(Q_1(B)\)，基线策略的Qini曲线称为\(\overline Q(B)\)。在\(B=0.1\)时，\(Q_1(0.1) - \overline Q(0.1)\)的估计值为

est, std_err = qini_1.difference_gain(qini_baseline, 0.1)
est, std_err

(0.12102711982945671, 0.024068445449392815)

也就是说，在每单位预算为0.1的情况下，使用给定的臂1 CATE函数进行目标定位相对于随机目标定位时增益增加的95%置信区间为

[est - 1.96*std_err, est + 1.96*std_err]

[0.0738529667486468, 0.16820127291026662]

（任意曲线上的点可以使用difference_gain方法进行比较，生成配对的标准误差，这些误差考虑了在同一测试数据上拟合的Qini曲线之间的相关性）。

同样地，我们可以为第二个成本较高的臂估计一个Qini曲线 \(Q_2(B)\)

tau_hat_2 = tau_hat[:, 1]
cost_2 = cost[1]
IPW_scores_2 = IPW_scores[:, 1]

qini_2 = MAQ(n_bootstrap=200).fit(tau_hat_2, cost_2, IPW_scores_2)

qini_baseline.plot(show_ci=False) # Leave out CIs for legibility
qini_1.plot(color="blue", label="arm 1", show_ci=False)
qini_2.plot(color="red", label="arm 2", show_ci=False)

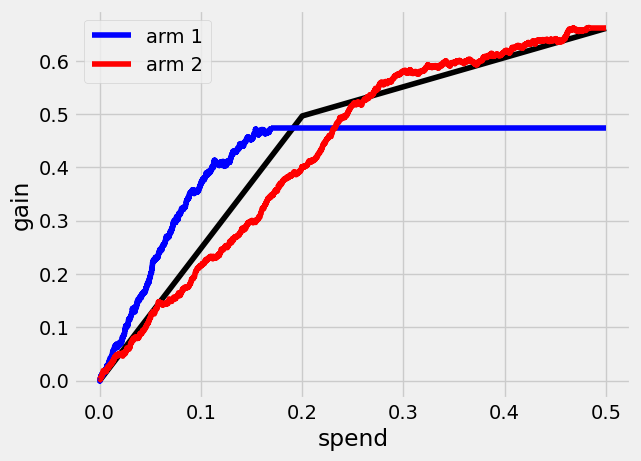
最后，我们可以看到使用双臂的Qini曲线\(Q(B)\)是什么样子的。

qini_ma = MAQ(n_bootstrap=200).fit(tau_hat, cost, IPW_scores)

qini_baseline.plot(show_ci=False)
qini_1.plot(color="blue", label="arm 1", show_ci=False)
qini_2.plot(color="red", label="arm 2", show_ci=False)
qini_ma.plot(color="green", label="both arms", show_ci=False)

单臂治疗规则的Qini曲线允许评估使用特定臂或目标函数进行定向的价值。将Qini推广到多个治疗臂使我们能够评估使用臂组合进行定向的价值。

在 \(B=0.3\) 时，使用双臂进行目标定位相对于仅使用第二臂的增益估计增加量，\(Q(0.3) - Q_2(0.3)\)，为

qini_ma.difference_gain(qini_2, 0.3)

(0.17003364056661086, 0.036733311977033105)

在这个例子中，多臂策略通过为每个测试集单元分配最具成本效益的处理来实现更大的收益。基础策略 \(\pi_B\) 看起来像

qini_ma.predict(0.3)

array([[0., 1.],
       [0., 1.],
       [1., 0.],
       ...,
       [1., 0.],
       [0., 1.],
       [0., 1.]])

其中行对应于\(\pi_B(X_i)\)，其中第\(k\)列包含1，如果在给定支出下将此臂分配给第\(i\)个单位是最优的（如果分配了控制臂，则所有条目为0）。策略的另一种表示是在处理臂集合{0, 1, 2}中取值

qini_ma.predict(0.3, prediction_type="vector")

array([2, 2, 1, ..., 1, 2, 2])

除了比较不同Qini曲线上的点外，我们还可以通过估计两条曲线之间到最大\(\overline B\)的面积来比较一系列支出水平。估计绿色和红色曲线之间到\(\overline B=0.5\)的面积，即积分\(\int_{0}^{0.5} (Q(B) - Q_2(B))dB\)，的估计值和标准误差为

qini_ma.integrated_difference(qini_2, 0.5)

(0.12548196750671803, 0.02945344768121884)