贝叶斯加性回归树：介绍#

from pathlib import Path

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pymc_bart as pmb

from sklearn.model_selection import train_test_split

%config InlineBackend.figure_format = "retina"

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.9.2+10.g547bcb481

RANDOM_SEED = 5781
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")

BART概述#

贝叶斯加性回归树（BART）是一种非参数回归方法。如果我们有一些协变量 \(X\) 并且我们想用它们来建模 \(Y\)，一个BART模型（省略先验）可以表示为：

\[Y = f(X) + \epsilon\]

我们使用一个由\(m\)个回归树组成的和来建模\(f\)，并且\(\epsilon\)是一些噪声。在最典型的例子中，\(\epsilon\)是正态分布的，\(\mathcal{N}(0, \sigma)\)。因此我们也可以写成：

\[Y \sim \mathcal{N}(\mu=BART(X), \sigma)\]

原则上，没有什么限制我们使用树的和来建模其他关系。例如，我们可能有：

\[Y \sim \text{Poisson}(\mu=BART(X))\]

BART 是贝叶斯的一个原因是使用了回归树的先验。先验是这样定义的，它们倾向于浅层树，且叶子的值接近于零。一个关键的想法是，单个 BART 树在拟合数据方面并不是很好，但当我们对许多这样的树求和时，我们会得到一个良好且灵活的近似。

使用BART进行煤矿开采#

为了更好地理解BART在实际中的应用，我们将使用经典的煤矿灾难数据集。这是PyMC中的一个经典示例。与将此问题视为具有两个泊松分布的切换点模型不同，我们将此问题视为具有泊松响应的非参数回归（这通常在泊松过程或Cox过程的背景下讨论，但我们不需要深入这些技术细节）。有关类似示例，但使用高斯过程，请参见1或2。由于我们的数据只是一个带有日期的单列数据，我们需要进行一些预处理。我们将对数据进行离散化处理，就像构建直方图一样。我们将使用箱子的中心作为变量\(X\)，并将每个箱子的计数作为变量\(Y\)。

try:
    coal = np.loadtxt(Path("..", "data", "coal.csv"))
except FileNotFoundError:
    coal = np.loadtxt(pm.get_data("coal.csv"))

# discretize data
years = int(coal.max() - coal.min())
bins = years // 4
hist, x_edges = np.histogram(coal, bins=bins)
# compute the location of the centers of the discretized data
x_centers = x_edges[:-1] + (x_edges[1] - x_edges[0]) / 2
# xdata needs to be 2D for BART
x_data = x_centers[:, None]
# express data as the rate number of disaster per year
y_data = hist

在 PyMC 中，BART 变量的定义与其他随机变量非常相似。一个重要的区别是，我们必须将我们的 Xs 和 Ys 传递给 BART 变量，这些信息在采样树时使用，树的总和的先验是如此巨大，如果没有来自我们数据的任何信息，这将是一项不可能的任务。

这里我们也明确表示我们将使用20棵树的和（m=20）。像20这样的少量树对于像这样的简单模型来说可能已经足够好，并且在建模的早期阶段，当我们可能希望尽可能快地尝试一些东西以更好地理解哪些模型可能适合我们的问题时，它也可以作为更复杂模型的快速近似。在这些情况下，一旦我们对真正喜欢的模型有了更多的确定性，我们就可以通过增加m来改进近似，在文献中通常会发现使用50、100或200这样的数字可以获得良好的结果。

with pm.Model() as model_coal:
    μ_ = pmb.BART("μ_", X=x_data, Y=np.log(y_data), m=20)
    μ = pm.Deterministic("μ", pm.math.exp(μ_))
    y_pred = pm.Poisson("y_pred", mu=μ, observed=y_data)
    idata_coal = pm.sample(random_seed=RANDOM_SEED)

Multiprocess sampling (4 chains in 4 jobs)
PGBART: [μ_]
100.00% [8000/8000 00:11<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 11 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details

在检查结果之前，我们需要再讨论一个细节，BART变量总是在实线上进行采样，这意味着原则上我们可以得到从\(-\infty\)到\(\infty\)的值。因此，我们可能需要像处理标准广义线性模型那样对它们的值进行转换，例如在model_coal中我们计算了pm.math.exp(μ_)，因为泊松分布期望的值是从0到\(\infty\)。这是常规操作，新奇之处在于我们可能需要对Y的值应用逆变换，就像我们在前一个模型中所做的那样，我们取了\(\log(Y)\)。这样做的主要原因是Y的值用于为树的总和和叶节点的方差获取合理的初始值。因此，应用逆变换是一种简单的方法来提高结果的效率和准确性。我们是否应该对每种可能的似然都这样做？不，如果我们使用BART作为正态分布、学生T分布或非对称拉普拉斯分布的位置参数，我们不需要做任何事情，因为这些参数的支持也是实线。一个非平凡的例外是伯努利似然（或n=1的二项分布），在这种情况下，我们需要对BART变量应用逻辑函数，但不需要对其逆变换来转换Y，PyMC-BART已经处理了那个特殊情况。

好的，现在让我们看看 model_coal 的结果。

_, ax = plt.subplots(figsize=(10, 6))

rates = idata_coal.posterior["μ"] / 4
rate_mean = rates.mean(dim=["draw", "chain"])
ax.plot(x_centers, rate_mean, "w", lw=3)
ax.plot(x_centers, y_data / 4, "k.")
az.plot_hdi(x_centers, rates, smooth=False)
az.plot_hdi(x_centers, rates, hdi_prob=0.5, smooth=False, plot_kwargs={"alpha": 0})
ax.plot(coal, np.zeros_like(coal) - 0.5, "k|")
ax.set_xlabel("years")
ax.set_ylabel("rate");
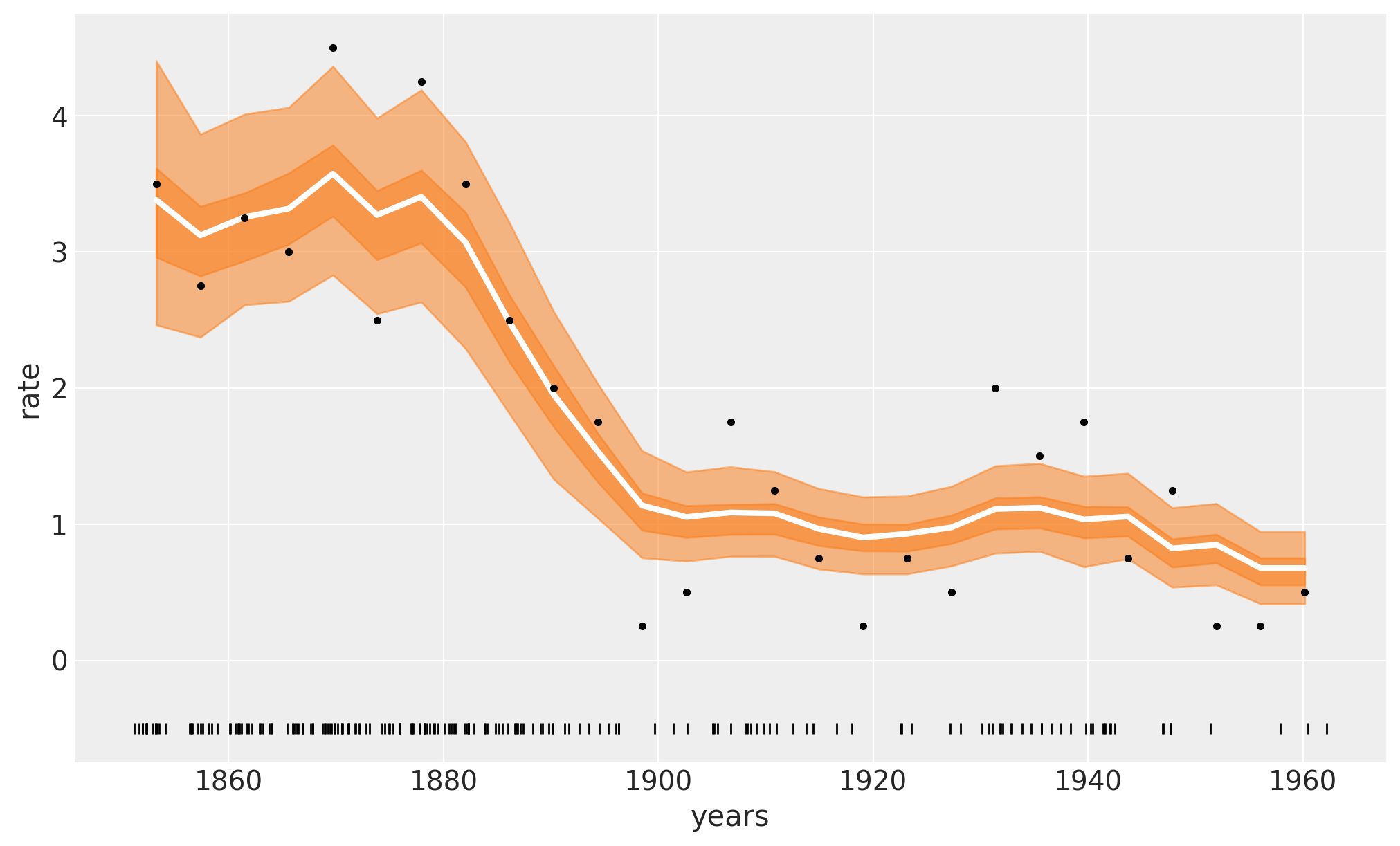
../../../_images/f86dc9e4e1be3da5e1ba618059237d994163ea13061f489ef07bd7fffce08982.png

下图中的白线显示了事故的中位数发生率。较深的橙色带表示HDI 50%，较浅的橙色带表示94%。我们可以看到1880年到1900年间煤矿事故迅速减少。欢迎将这些结果与原始的PyMC简介概述示例中的结果进行比较。

在前面的图中，白线是4000次后验抽样的均值，而每一次后验抽样都是对m=20棵树的求和。

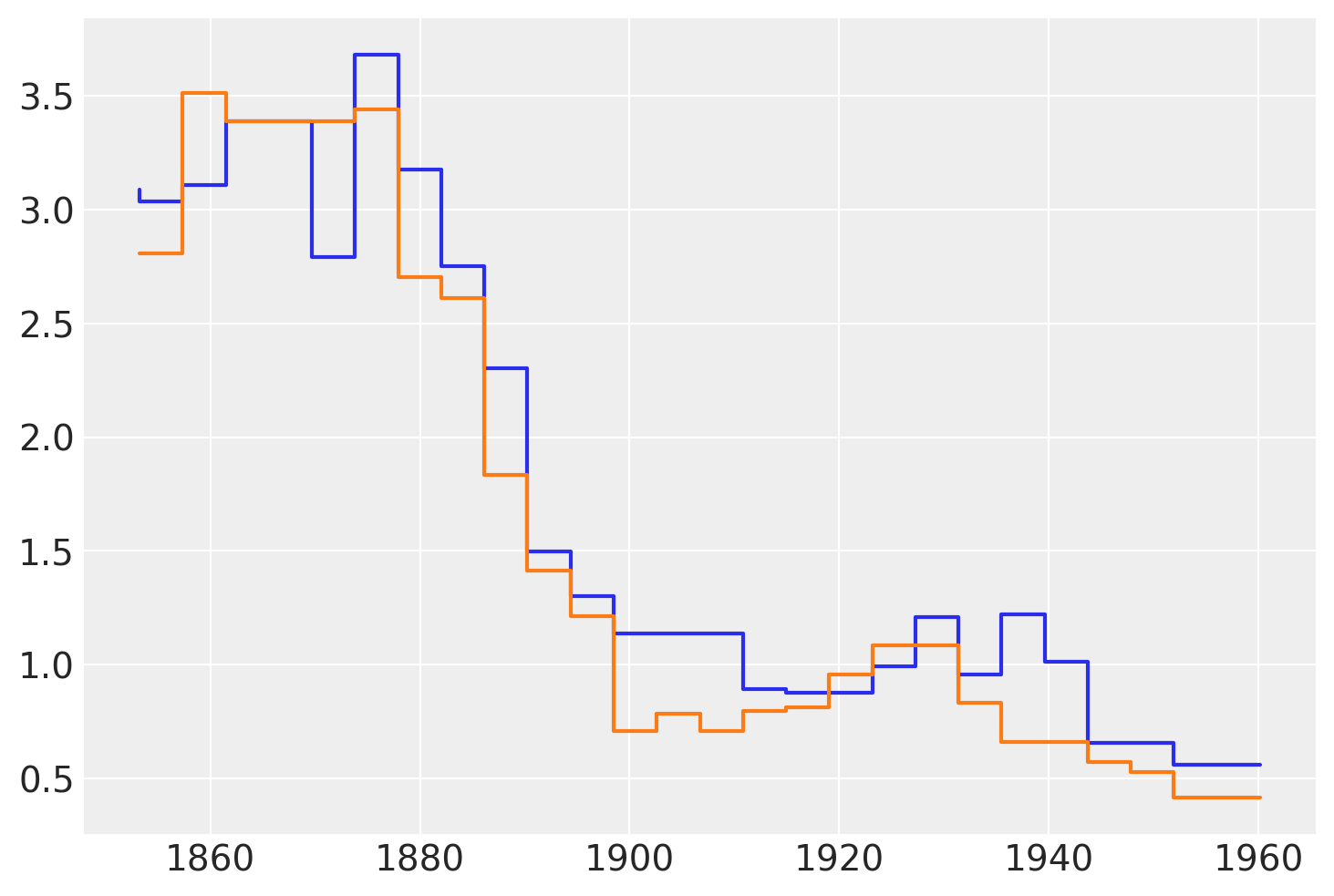
下图显示了来自\(\mu\)后验的两个样本。我们可以看到这些函数并不平滑。这是正常的，并且是使用回归树的直接结果。树可以被视为表示分段函数的一种方式，而分段函数的和只是另一个分段函数。因此，当使用BART时，我们需要知道我们假设分段函数对于我们的问题是足够好的近似。在实践中，这通常是正确的，因为我们通常对许多树进行求和，通常是50、100或200这样的值。 此外，我们通常对后验分布进行平均。所有这些都使得“步骤更平滑”，即使我们从未真正得到一个平滑的函数，例如使用高斯过程或样条曲线。一个很好的理论结果告诉我们，在\(m \to \infty\)的极限情况下，BART先验收敛于一个处处不可微的高斯过程。

下图显示了从后验分布中抽取的两个\(\mu\)样本。

plt.step(x_data, rates.sel(chain=0, draw=[3, 10]).T);
../../../_images/00bcfc29cbcbfeae0ee56821ae329134b7a3757fb3d0f0c05876b46961f2d398.png

与BART一起骑自行车#

为了探索PyMC-BART提供的其他功能，我们现在将转向一个不同的示例。在这个示例中，我们有关于城市中自行车租赁数量的数据，并且我们选择了四个协变量；即一天中的小时，温度，湿度，以及是否是工作日或周末。该数据集是bike_sharing_dataset的一个子集。

try:
    bikes = pd.read_csv(Path("..", "data", "bikes.csv"))
except FileNotFoundError:
    bikes = pd.read_csv(pm.get_data("bikes.csv"))

features = ["hour", "temperature", "humidity", "workingday"]

X = bikes[features]
Y = bikes["count"]

with pm.Model() as model_bikes:
    α = pm.Exponential("α", 1)
    μ = pmb.BART("μ", X, np.log(Y), m=50)
    y = pm.NegativeBinomial("y", mu=pm.math.exp(μ), alpha=α, observed=Y)
    idata_bikes = pm.sample(compute_convergence_checks=False, random_seed=RANDOM_SEED)

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>NUTS: [α]
>PGBART: [μ]
100.00% [8000/8000 00:41<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 41 seconds.

收敛诊断#

要检查BART模型的采样收敛性，我们推荐一种两步法。

  • 对于非BART变量（如\(\alpha\)在model_bikes中），我们遵循标准建议，如检查R-hat（<= 1.01）和ESS（< 100x链数）数值诊断，以及使用迹图或更好的rankplots

  • 对于BART变量，我们建议使用pmb.plot_convergence函数。

我们可以看到以下检查：

az.plot_trace(idata_bikes, var_names=["α"], kind="rank_bars");
../../../_images/23627706088c2ed0708ddd450d30c1257a30b686ea65ecde735b9e9dc2d5b146.png 
pmb.plot_convergence(idata_bikes, var_name="μ");
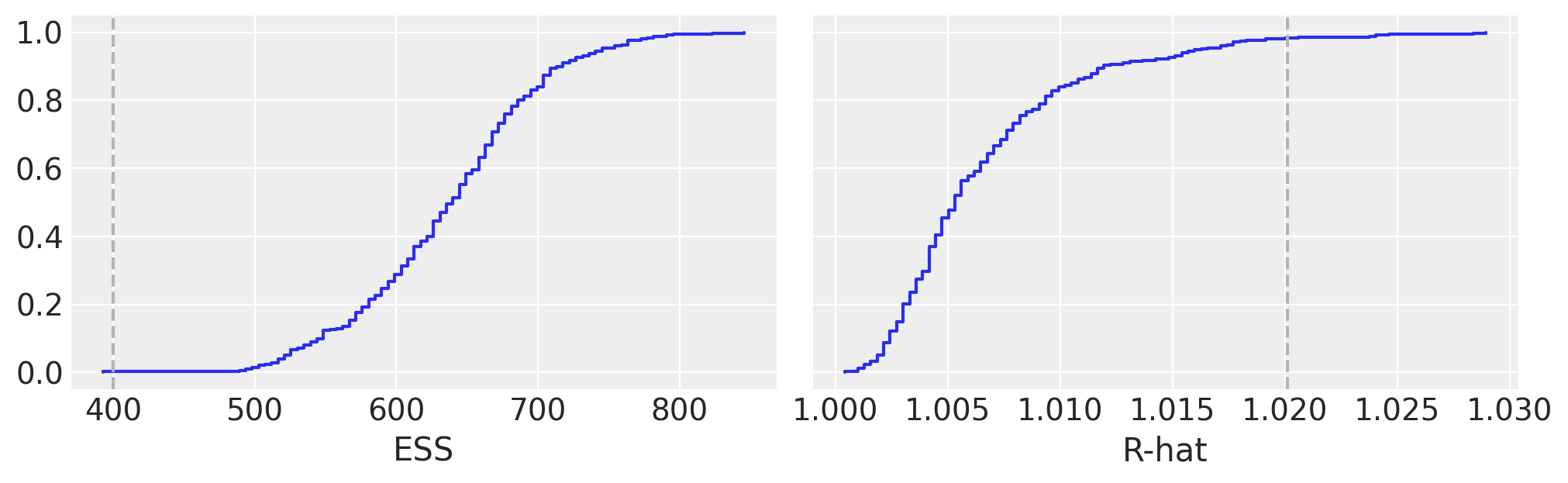
../../../_images/891cde55a86615a9c746cd448c4eeb697b4290d3a4f3a40e8b0942c433412dc5.png

在BART文献中，BART变量的诊断有时被认为不如非BART变量的诊断重要，主要论点是潜在变量的个体估计值没有直接的兴趣，相反，我们只应关心我们如何很好地估计整个函数/回归。

我们反而认为检查BART变量的收敛性是贝叶斯工作流程中的一个重要部分。使用pmb.plot_convergence的主要原因通常是BART变量将是一个大向量（我们为每个观测值估计一个分布），因此我们需要检查大量的诊断信息。此外，R-hat阈值1.01并不是一个硬性阈值，这个值是假设检查一个或几个R-hat（并且链足够长以准确估计其自相关性）而选择的，如果我们观察到大量的R-hat，即使我们的推断没有问题，其中一些预计会超过1.01阈值（或我们选择的任何阈值）。因此，公平的分析应包括多重比较调整，而这正是pmb.plot_convergence自动为您完成的。那么，如何解读其输出呢？我们有两个面板，一个用于ESS，一个用于R-hat。蓝线是这些值的经验累积分布，对于ESS，我们希望整个曲线在虚线之上，而对于R-hat，我们希望曲线完全在虚线之下。在前面的图中，我们可以看到我们勉强达到了ESS的要求，而对于R-hat，我们有非常少的值超过阈值。我们的结果是无用的吗？很可能不是。但为了确保，我们可能需要多抽取一些样本。

部分依赖图#

为了帮助我们解释模型的结果，我们将使用部分依赖图。这是一种显示一个协变量对预测变量的边际效应的图。也就是说，当我们对所有其他协变量（\(X_j, \forall j \not = i\)）进行平均时，协变量 \(X_i\) 对 \(Y\) 的影响是什么。这种类型的图并不专属于BART。但它们经常在BART文献中使用。PyMC-BART提供了一个实用函数，可以从BART随机变量生成这种图。

pmb.plot_pdp(μ, X=X, Y=Y, grid=(2, 2), func=np.exp, var_discrete=[3]);
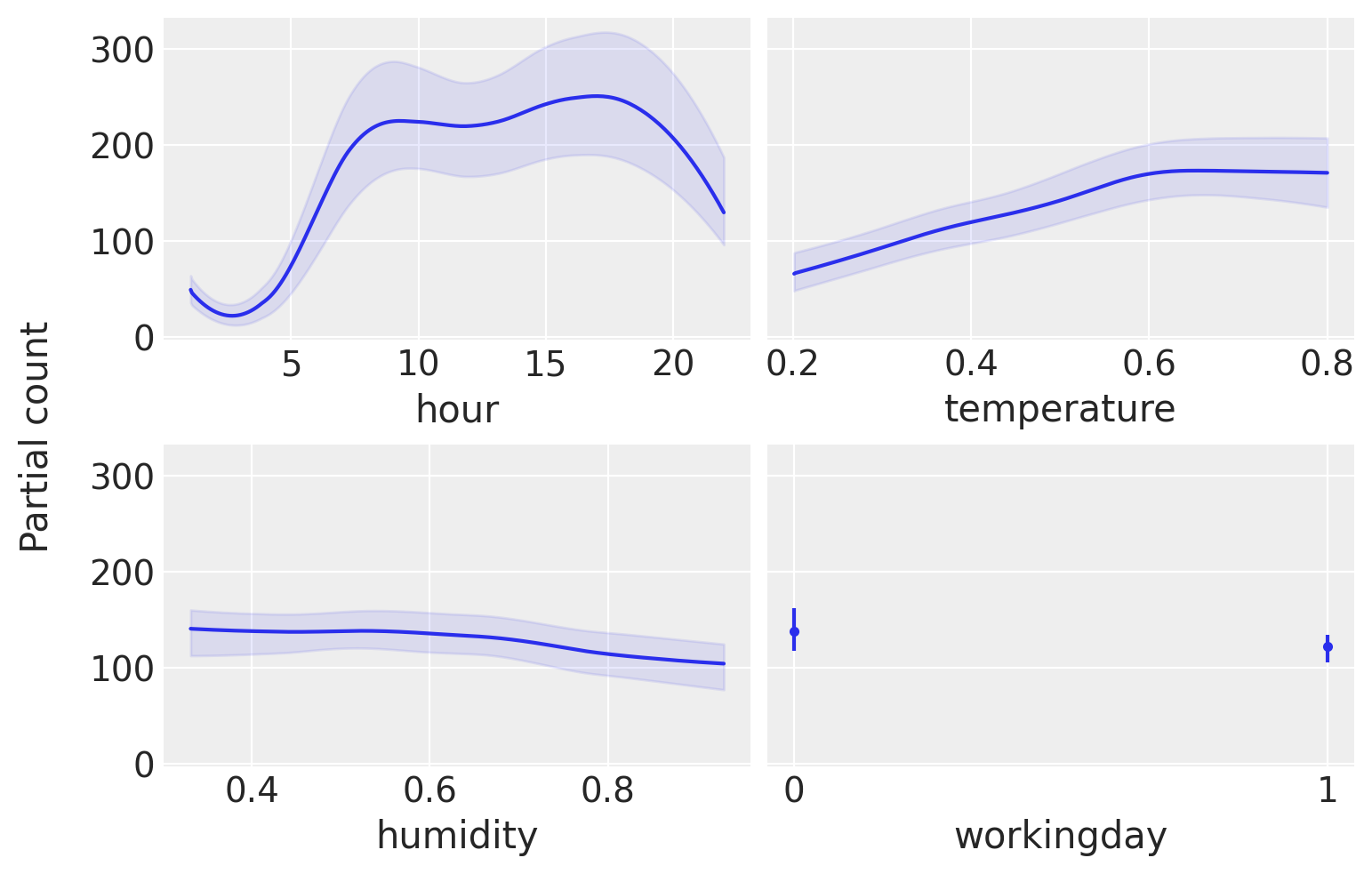
../../../_images/06e60161631d6b40d9285b41de04a11aae32e7d21419b6597833163389171f43.png

从这张图中，我们可以看到每个协变量对预测值的主要影响。这非常有用，因为我们可以恢复超越单调递增或递减效应的复杂关系。例如，对于小时协变量，我们可以看到在8点和17点附近有两个峰值，而在午夜有一个最小值。

在解释部分依赖图时，我们应该注意这个图中的假设。首先，我们假设变量是独立的。例如，在计算hour的影响时，我们必须边缘化temperature的影响，这意味着在计算hour=0的部分依赖值时，我们包含了所有观测到的温度值，这可能包括在午夜未观测到的温度，因为较低的温度比较高的温度更可能出现。我们看到的只是平均值，所以如果对于一个协变量，一半的值与预测变量正相关，另一半负相关，部分依赖图将是平坦的，因为它们的贡献会相互抵消。这是一个可以通过使用个体条件期望图pmb.plot_ice(...)来解决的问题。请注意，所有这些假设都是部分依赖图的假设，而不是我们模型的假设！事实上，BART可以很容易地适应变量之间的交互（尽管BART中的先验规范化了高阶交互）。有关解释机器学习模型的更多信息，您可以查看“可解释的机器学习”书籍[Molnar, 2019]。

最后，与其他回归方法一样，我们应该注意，我们在单个变量上看到的效果是基于其他变量的包含条件。例如，虽然湿度看起来基本上是平坦的，这意味着这个协变量对使用自行车的数量影响很小。这可能是因为湿度和温度在某种程度上是相关的，一旦我们在模型中包含了温度，湿度就不会提供太多额外的信息。例如，尝试再次拟合模型，但这次将湿度作为单一协变量，然后再次拟合模型，将小时作为单一协变量。你应该会看到，这个单变量模型的结果与之前小时协变量的图非常相似，但对于湿度协变量则不那么相似。

变量重要性#

正如我们在前一节中看到的，部分依赖图可以可视化并让我们了解每个协变量对预测结果的贡献程度。此外，PyMC-BART 提供了一种新颖的方法来评估模型中每个变量的重要性。您可以在下图中看到一个示例。

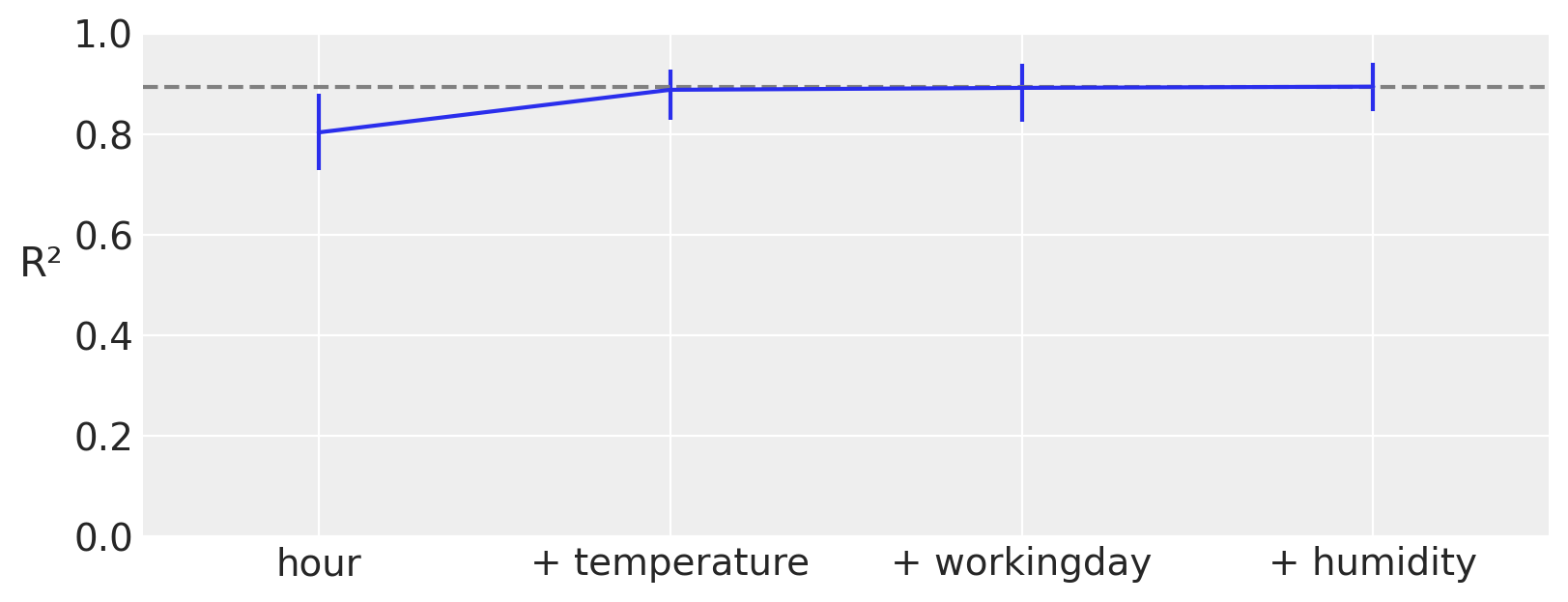
在x轴上我们有协变量的数量，在y轴上我们有R²（皮尔逊相关系数的平方），表示完整模型（包含所有变量）的预测结果与受限模型（仅包含部分变量）的预测结果之间的相关性。

在这个例子中，最重要的变量是hour，然后是temperature、humidity，最后是workingday。请注意，第一个R²的值是仅包含变量hour的模型的值，第二个R²是包含两个变量hour和temperature的模型的值，依此类推。除了这个排名，我们还可以看到，即使是一个仅包含单个组件hour的模型，也非常接近完整模型。更重要的是，包含两个组件hour和temperature的模型在平均水平上与完整模型无法区分。误差条表示后验预测分布的94% HDI。这意味着我们应该期望仅包含hour和temperature的模型与包含四个变量hour、temperature、humidity和workingday的模型具有相似的预测性能。

pmb.plot_variable_importance(idata_bikes, μ, X);
../../../_images/e1fd6d43f2ef83ac8d6a10c0629dc2e7c3948090e5d4947c7c65b0f17b6fcda7.png

plot_variable_importance 之所以快速，是因为它做了两个假设：

  • 变量的排名是通过一个简单的启发式方法计算的。我们只是统计一个变量在所有回归树中被包含的次数。直觉上，如果一个变量是重要的，它应该在拟合的树中比不重要的变量出现得更频繁。

  • 用于计算R²的预测值来自已经拟合好的树。例如，为了估计一个包含变量hour的BART模型的效果，我们修剪不包含该变量的分支。这使得计算速度大大加快，因为我们不需要找到一组新的树。

不使用“计数启发式”。它还可以执行反向搜索，pmb.plot_variable_importance(..., method="backward")。在内部，这将计算完整模型的R²，然后计算所有比完整模型少一个变量的模型的R²，接着计算所有比完整模型少两个变量的模型的R²，依此类推。在每个阶段，我们丢弃给出最低R²的变量。反向方法会更慢，因为我们需要为更多模型计算预测。

样本外预测#

在本节中，我们希望展示如何使用BART进行样本外预测。我们将使用与之前相同的数据集，但这次我们将数据分为训练集和测试集。我们将使用训练集来拟合模型，并使用测试集来评估模型。

回归#

让我们首先将这些数据建模为一个回归问题。在这种情况下，我们随机将数据分为训练集和测试集。

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=RANDOM_SEED)

现在，我们使用与上面相同的模型，但这次使用共享变量来表示协变量，以便我们随后可以替换它们以生成样本外预测。

with pm.Model() as model_oos_regression:
    X = pm.MutableData("X", X_train)
    Y = Y_train
    α = pm.Exponential("α", 1)
    μ = pmb.BART("μ", X, np.log(Y))
    y = pm.NegativeBinomial("y", mu=pm.math.exp(μ), alpha=α, observed=Y, shape=μ.shape)
    idata_oos_regression = pm.sample(random_seed=RANDOM_SEED)
    posterior_predictive_oos_regression_train = pm.sample_posterior_predictive(
        trace=idata_oos_regression, random_seed=RANDOM_SEED
    )

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>NUTS: [α]
>PGBART: [μ]
100.00% [8000/8000 00:48<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 49 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
Sampling: [y]
100.00% [4000/4000 00:00<00:00]

接下来，我们替换模型中的数据并从后验预测分布中进行采样。

with model_oos_regression:
    X.set_value(X_test)
    posterior_predictive_oos_regression_test = pm.sample_posterior_predictive(
        trace=idata_oos_regression, random_seed=RANDOM_SEED
    )

Sampling: [y, μ]
100.00% [4000/4000 00:21<00:00]

最后，我们可以将后验预测分布与观测数据进行比较。

Hide code cell source 
fig, ax = plt.subplots(
    nrows=2, ncols=1, figsize=(8, 7), sharex=True, sharey=True, layout="constrained"
)

az.plot_ppc(
    data=posterior_predictive_oos_regression_train, kind="cumulative", observed_rug=True, ax=ax[0]
)
ax[0].set(title="Posterior Predictive Check (train)", xlim=(0, 1_000))

az.plot_ppc(
    data=posterior_predictive_oos_regression_test, kind="cumulative", observed_rug=True, ax=ax[1]
)
ax[1].set(title="Posterior Predictive Check (test)", xlim=(0, 1_000));
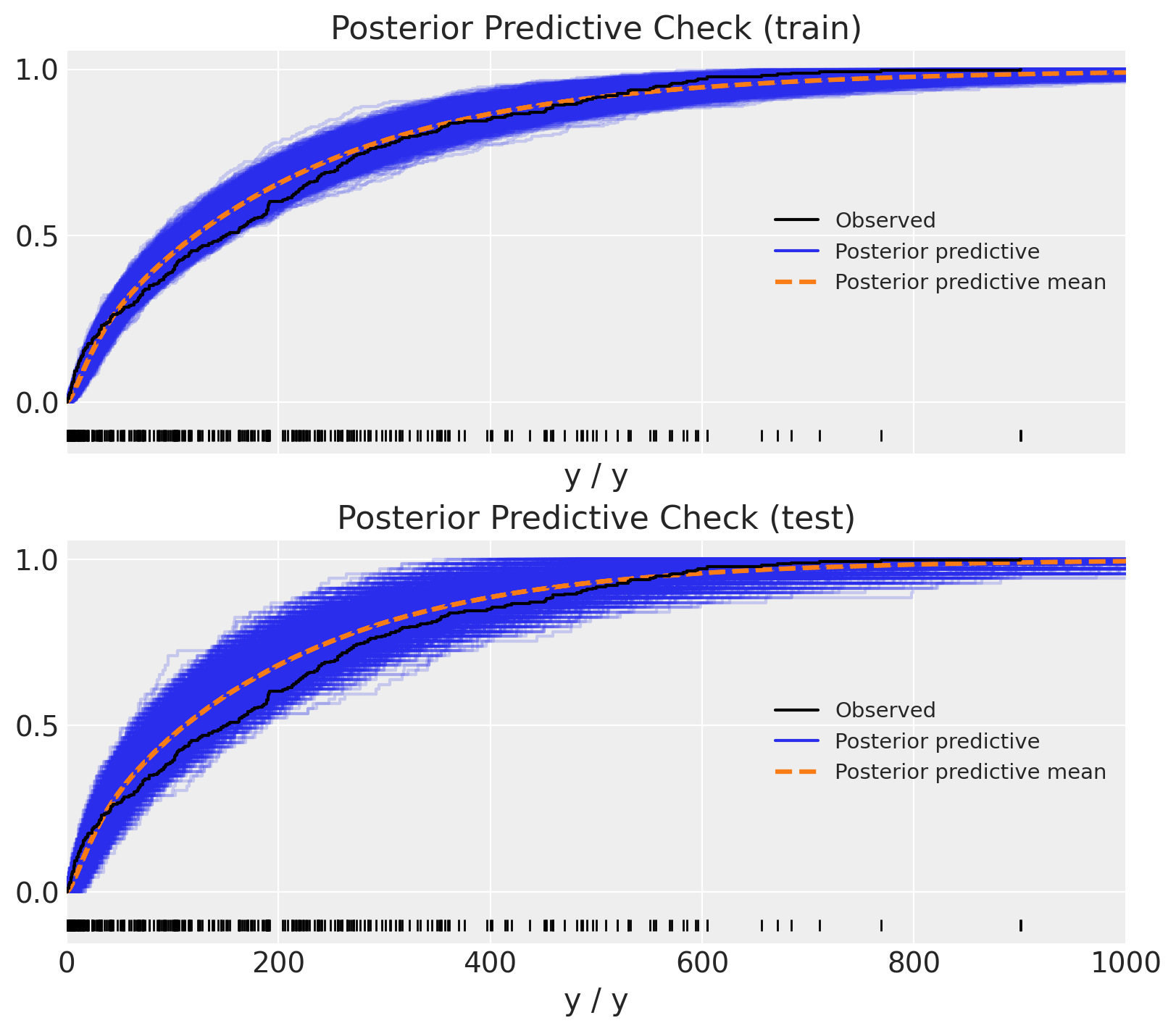
../../../_images/3922feacdf790c18d52a747a346381ef6ff9973663005f06426a7d07befb09cf.png

耶！结果看起来相当合理 🙂！

时间序列#

我们可以从时间序列的角度使用hour特征来查看相同的数据。从这个角度来看，我们需要确保不混洗数据，以免泄露信息。因此，我们使用hour特征来定义训练-测试分割。

train_test_hour_split = 19

train_bikes = bikes.query("hour <= @train_test_hour_split")
test_bikes = bikes.query("hour > @train_test_hour_split")

X_train = train_bikes[features]
Y_train = train_bikes["count"]

X_test = test_bikes[features]
Y_test = test_bikes["count"]

然后我们可以运行相同的模型（但使用不同的输入数据！）并生成如上所述的样本外预测。

with pm.Model() as model_oos_ts:
    X = pm.MutableData("X", X_train)
    Y = Y_train
    α = pm.Exponential("α", 1 / 10)
    μ = pmb.BART("μ", X, np.log(Y))
    y = pm.NegativeBinomial("y", mu=pm.math.exp(μ), alpha=α, observed=Y, shape=μ.shape)
    idata_oos_ts = pm.sample(random_seed=RANDOM_SEED)
    posterior_predictive_oos_ts_train = pm.sample_posterior_predictive(
        trace=idata_oos_ts, random_seed=RANDOM_SEED
    )

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>NUTS: [α]
>PGBART: [μ]
100.00% [8000/8000 00:47<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 48 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
Sampling: [y]
100.00% [4000/4000 00:00<00:00]

我们生成样本外预测。

with model_oos_ts:
    X.set_value(X_test)
    posterior_predictive_oos_ts_test = pm.sample_posterior_predictive(
        trace=idata_oos_ts, random_seed=RANDOM_SEED
    )

Sampling: [y, μ]
100.00% [4000/4000 00:20<00:00]

与上述类似，我们可以将后验预测分布与观测数据进行比较。

Hide code cell source 
fig, ax = plt.subplots(
    nrows=2, ncols=1, figsize=(8, 7), sharex=True, sharey=True, layout="constrained"
)

az.plot_ppc(data=posterior_predictive_oos_ts_train, kind="cumulative", observed_rug=True, ax=ax[0])
ax[0].set(title="Posterior Predictive Check (train)", xlim=(0, 1_000))

az.plot_ppc(data=posterior_predictive_oos_ts_test, kind="cumulative", observed_rug=True, ax=ax[1])
ax[1].set(title="Posterior Predictive Check (test)", xlim=(0, 1_000));
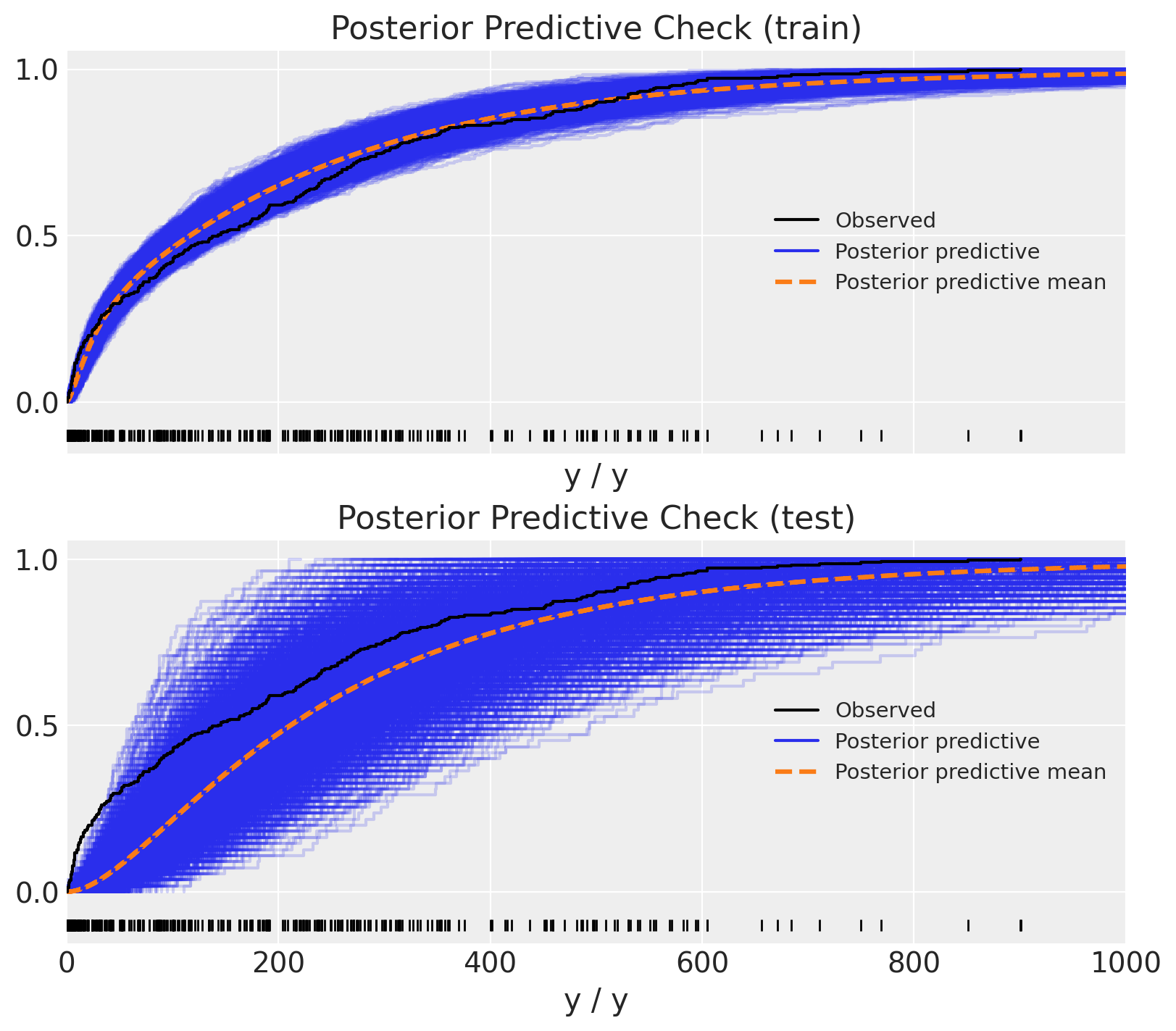
../../../_images/a3d1a1abf3684868cc9eec30415f5078513bd8996691b61cecf2edca51622217.png

哇！这看起来不太对劲！测试集上的预测看起来非常奇怪 🤔。为了更好地理解发生了什么，我们可以将预测绘制为时间序列：

Hide code cell source 
fig, ax = plt.subplots(figsize=(12, 6))
az.plot_hdi(
    x=X_train.index,
    y=posterior_predictive_oos_ts_train.posterior_predictive["y"],
    hdi_prob=0.94,
    color="C0",
    fill_kwargs={"alpha": 0.2, "label": r"94$\%$ HDI (train)"},
    smooth=False,
    ax=ax,
)
az.plot_hdi(
    x=X_train.index,
    y=posterior_predictive_oos_ts_train.posterior_predictive["y"],
    hdi_prob=0.5,
    color="C0",
    fill_kwargs={"alpha": 0.4, "label": r"50$\%$ HDI (train)"},
    smooth=False,
    ax=ax,
)
ax.plot(X_train.index, Y_train, label="train (observed)")
az.plot_hdi(
    x=X_test.index,
    y=posterior_predictive_oos_ts_test.posterior_predictive["y"],
    hdi_prob=0.94,
    color="C1",
    fill_kwargs={"alpha": 0.2, "label": r"94$\%$ HDI (test)"},
    smooth=False,
    ax=ax,
)
az.plot_hdi(
    x=X_test.index,
    y=posterior_predictive_oos_ts_test.posterior_predictive["y"],
    hdi_prob=0.5,
    color="C1",
    fill_kwargs={"alpha": 0.4, "label": r"50$\%$ HDI (test)"},
    smooth=False,
    ax=ax,
)
ax.plot(X_test.index, Y_test, label="test (observed)")
ax.axvline(X_train.shape[0], color="k", linestyle="--", label="train/test split")
ax.legend(loc="center left", bbox_to_anchor=(1, 0.5))
ax.set(
    title="BART model predictions for bike rentals",
    xlabel="observation index",
    ylabel="number of rentals",
);
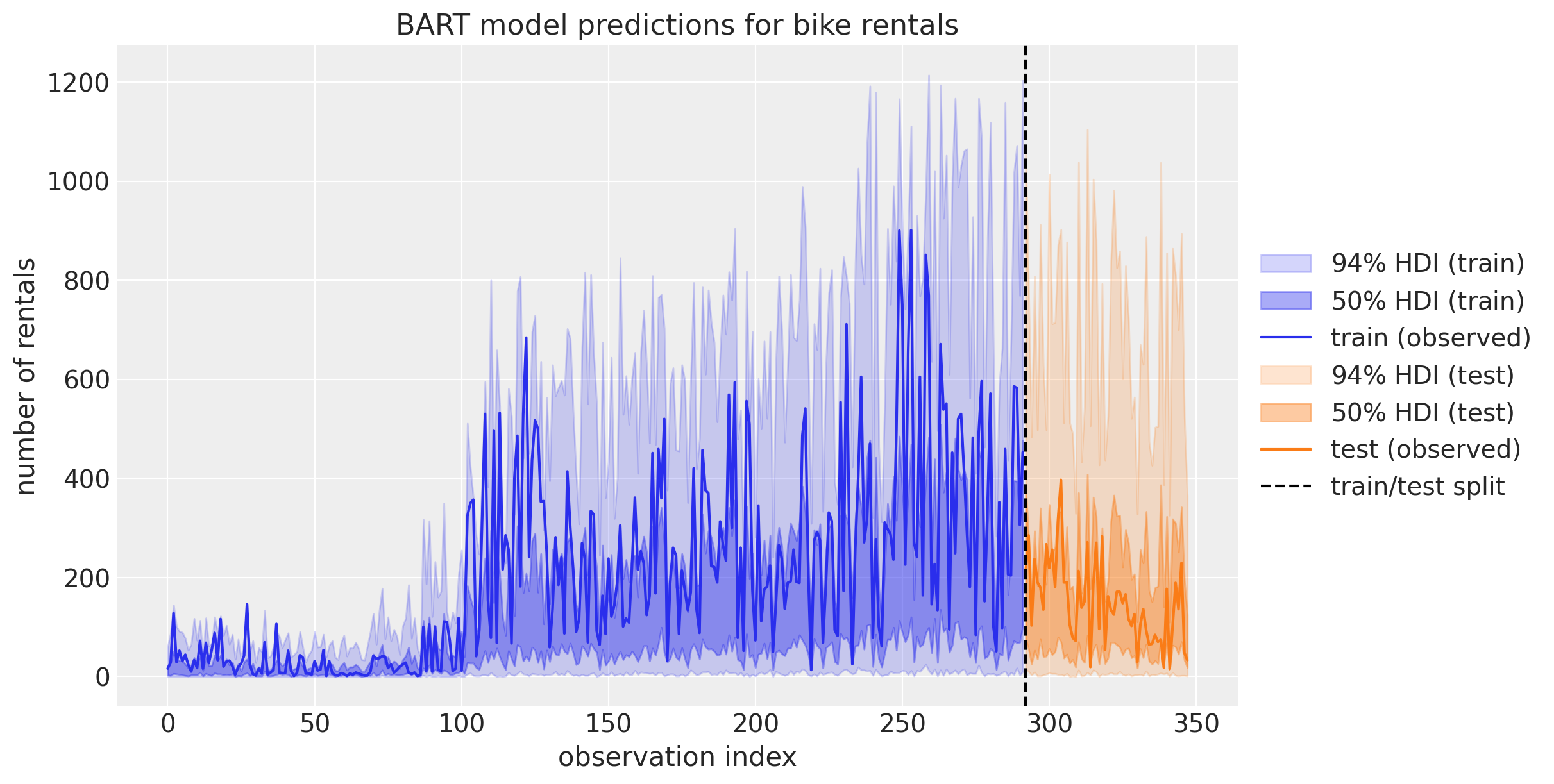
../../../_images/f73c7981c7f8a49897079698a271e441df6f42fd042ed61762b40beda97726ba.png

这个图帮助我们理解测试集表现不佳的原因：回想一下，在初始模型的变量重要性排名中，我们看到hour是最重要的预测因子。另一方面，我们的训练数据只看到hour值直到\(19\)（因为这是我们的训练-测试阈值）。当BART学习如何划分（训练）数据时，它无法区分hour值在\(20\)和\(22\)之间的情况。它只关心这两个值都大于\(19\)。理解这一点在使用BART时非常重要！这解释了为什么如果时间序列中存在趋势成分，就不应该使用BART进行时间序列预测。在这种情况下，最好先对数据进行去趋势处理，用BART对剩余部分建模，并用不同的模型对趋势进行建模。

作者#

  • 由Osvaldo Martin于2021年12月撰写（pymc-examples#259）

  • 由Osvaldo Martin于2022年5月更新 (pymc-examples#323)

  • 由Osvaldo Martin于2022年9月更新

  • 由Osvaldo Martin于2022年11月更新

  • Juan Orduz 在 2023 年 1 月添加了样本外部分

  • 由Osvaldo Martin于2023年3月更新

  • 由Osvaldo Martin于2023年11月更新

参考资料#

[1]

Miriana Quiroga, Pablo G Garay, Juan M. Alonso, Juan Martin Loyola, 和 Osvaldo A Martin. 贝叶斯加性回归树用于概率编程。2022年。URL: https://arxiv.org/abs/2206.03619, doi:10.48550/ARXIV.2206.03619.

[2]

克里斯托夫·莫尔纳. 可解释的机器学习. 克里斯托夫·莫尔纳, 2019. URL: https://christophm.github.io/interpretable-ml-book/.

[3]

Osvaldo A Martin, Ravin Kumar, 和 Junpeng Lao. Python中的贝叶斯建模与计算. Chapman and Hall/CRC, 2021. doi:10.1201/9781003019169.

水印#

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sat Nov 18 2023

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.16.1

pymc      : 5.9.2+10.g547bcb481
pymc_bart : 0.5.3
numpy     : 1.24.4
matplotlib: 3.8.0
pandas    : 2.1.2
arviz     : 0.16.1

Watermark: 2.4.3