贝叶斯估计取代T检验#

import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v4.2.2

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(seed=42)

问题#

该模型复现了贝叶斯估计取代t检验中使用的示例 [Kruschke, 2013]。

几种统计推断程序涉及两组之间的比较。我们可能对一组是否大于另一组，或者仅仅是与另一组不同感兴趣。我们需要一个统计模型来进行这种比较，因为真正的差异通常伴随着测量或随机噪声，这使得我们无法仅从观察数据计算的差异中得出结论。

用于统计比较两个（或更多）样本的事实标准是使用统计检验。这涉及表达一个零假设，通常声称各组之间没有差异，并使用选定的检验统计量来确定在假设下观察数据的分布是否合理。当计算的检验统计量高于某个预先指定的阈值时，就会发生拒绝。

不幸的是，正确进行假设检验并不容易，而且其结果非常容易被误解。设置统计检验涉及用户做出的几个主观选择（例如 使用的统计检验、要检验的零假设、显著性水平），这些选择很少基于当前问题或决策来证明其合理性，而是通常基于完全任意的传统选择 [Johnson, 1999]。它向用户提供的证据是间接的、不完整的，并且通常夸大了反对零假设的证据 [Goodman, 1999]。

一种更具信息性和有效性的比较组的方法是基于估计而非检验，并且是由贝叶斯概率而非频率主义驱动的。也就是说，我们不是检验两个组是否不同，而是追求它们差异程度的估计，这从根本上更具信息性。此外，我们还包括与该差异相关的估计不确定性，这包括由于我们对模型参数缺乏了解而产生的不确定性（认知不确定性）以及系统固有的随机性引起的不确定性（偶然不确定性）。

示例：药物试验评估#

为了说明这种贝叶斯估计方法在实践中如何工作，我们将使用Kruschke [2013]中的一个虚构例子，关于评估药物临床试验。该试验旨在通过比较治疗组（接受药物）和对照组（接受安慰剂）的智商分数来评估一种“聪明药物”的有效性。治疗组和对照组分别有47人和42人。

# fmt: off
iq_drug = np.array([
    101, 100, 102, 104, 102, 97, 105, 105, 98, 101, 100, 123, 105, 103, 
    100, 95, 102, 106, 109, 102, 82, 102, 100, 102, 102, 101, 102, 102,
    103, 103, 97, 97, 103, 101, 97, 104, 96, 103, 124, 101, 101, 100,
    101, 101, 104, 100, 101
])

iq_placebo = np.array([
    99, 101, 100, 101, 102, 100, 97, 101, 104, 101, 102, 102, 100, 105,
    88, 101, 100, 104, 100, 100, 100, 101, 102, 103, 97, 101, 101, 100,
    101, 99, 101, 100, 100, 101, 100, 99, 101, 100, 102, 99, 100, 99
])
# fmt: on

df1 = pd.DataFrame({"iq": iq_drug, "group": "drug"})
df2 = pd.DataFrame({"iq": iq_placebo, "group": "placebo"})
indv = pd.concat([df1, df2]).reset_index()

sns.histplot(data=indv, x="iq", hue="group");
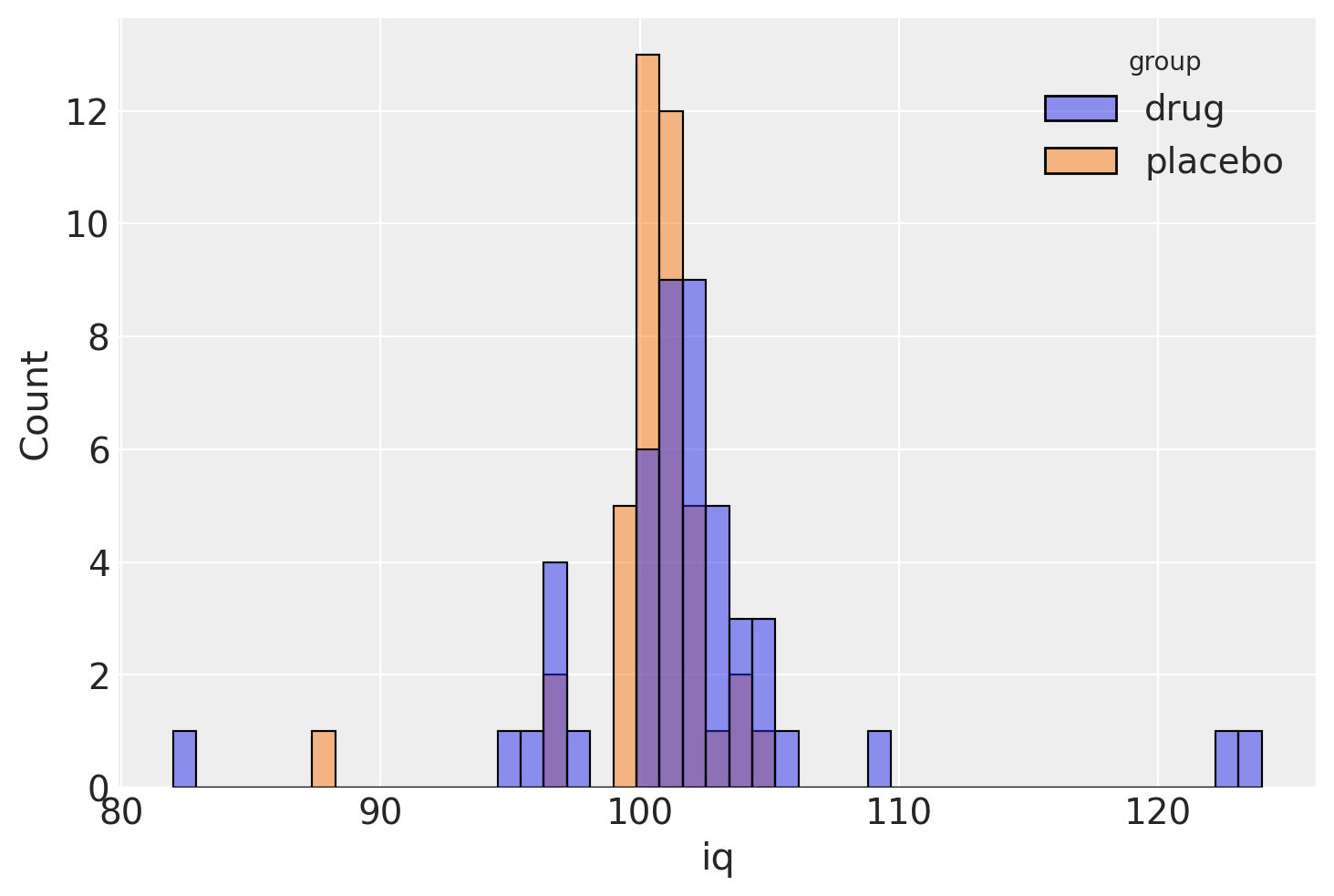
../../../_images/073035d65700ed87439b543ebee2d98e340346030646fed769fb9ec5d135f21f.png

贝叶斯推理方法的第一步是明确指定与问题相对应的完整概率模型。在这个例子中，Kruschke选择了一个学生t分布来描述每个组中分数的分布。这个选择增加了分析的稳健性，因为t分布相对于正态分布对异常值的敏感性较低。三参数学生t分布允许指定一个均值\(\mu\)、一个精度（逆方差）\(\lambda\)和一个自由度参数\(\nu\)：

\[f(x|\mu,\lambda,\nu) = \frac{\Gamma(\frac{\nu + 1}{2})}{\Gamma(\frac{\nu}{2})} \left(\frac{\lambda}{\pi\nu}\right)^{\frac{1}{2}} \left[1+\frac{\lambda(x-\mu)^2}{\nu}\right]^{-\frac{\nu+1}{2}}\]

自由度参数本质上指定了数据的“正态性”，因为较大的\(\nu\)值使分布趋近于正态分布，而较小的值（接近零）则导致尾部更重。因此，我们模型的似然函数指定如下：

\[y^{(treat)}_i \sim T(\nu, \mu_1, \sigma_1)\]
\[y^{(placebo)}_i \sim T(\nu, \mu_2, \sigma_2)\]

作为一个简化的假设，我们将假设两个组的正态程度 \(\nu\) 是相同的。当然，我们将为均值 \(\mu_k, k=1,2\) 和标准差 \(\sigma_k\) 设置单独的参数。由于均值是实数值，我们将对它们应用正态先验，并任意将超参数设置为数据的合并经验均值和两倍的合并经验标准差，这为这些量提供了非常分散的信息（并且重要的是，不偏袒其中任何一个 先验）。

\[\mu_k \sim N(\bar{x}, 2s)\]
mu_m = indv.iq.mean()
mu_s = indv.iq.std() * 2

with pm.Model() as model:
    group1_mean = pm.Normal("group1_mean", mu=mu_m, sigma=mu_s)
    group2_mean = pm.Normal("group2_mean", mu=mu_m, sigma=mu_s)

组标准差将在结果变量IQ的可变性合理范围内给予均匀先验。

在Kruschke的原始模型中，他使用了非常宽的均匀先验分布来表示组标准差，范围从合并的经验标准差除以1000到合并的标准差乘以1000。这是一个不合适的先验选择，因为关于人类认知测量的基本先验知识规定，变化不可能达到这个上限。IQ是一个标准化的测量，因此这限制了给定人群的IQ值的变异性。当你在这些值上放置如此宽的均匀先验时，你实际上是在给不可接受的值赋予大量的先验权重。在这个例子中，实际差异不大，但一般来说，最好尽可能多地应用你拥有的先验信息来参数化先验分布。

我们将设置组标准差具有\(\text{Uniform}(1,10)\)先验：

sigma_low = 10**-1
sigma_high = 10

with model:
    group1_std = pm.Uniform("group1_std", lower=sigma_low, upper=sigma_high)
    group2_std = pm.Uniform("group2_std", lower=sigma_low, upper=sigma_high)

我们按照 Kruschke 的做法，将 \(\nu\) 的先验设为指数分布，均值为 30；这为参数的区域分配了高先验概率，这些区域描述了在学生-T 分布下从正态到重尾数据的范围。

with model:
    nu_minus_one = pm.Exponential("nu_minus_one", 1 / 29.0)
    nu = pm.Deterministic("nu", nu_minus_one + 1)
    nu_log10 = pm.Deterministic("nu_log10", np.log10(nu))

az.plot_kde(rng.exponential(scale=29, size=10000) + 1, fill_kwargs={"alpha": 0.5});
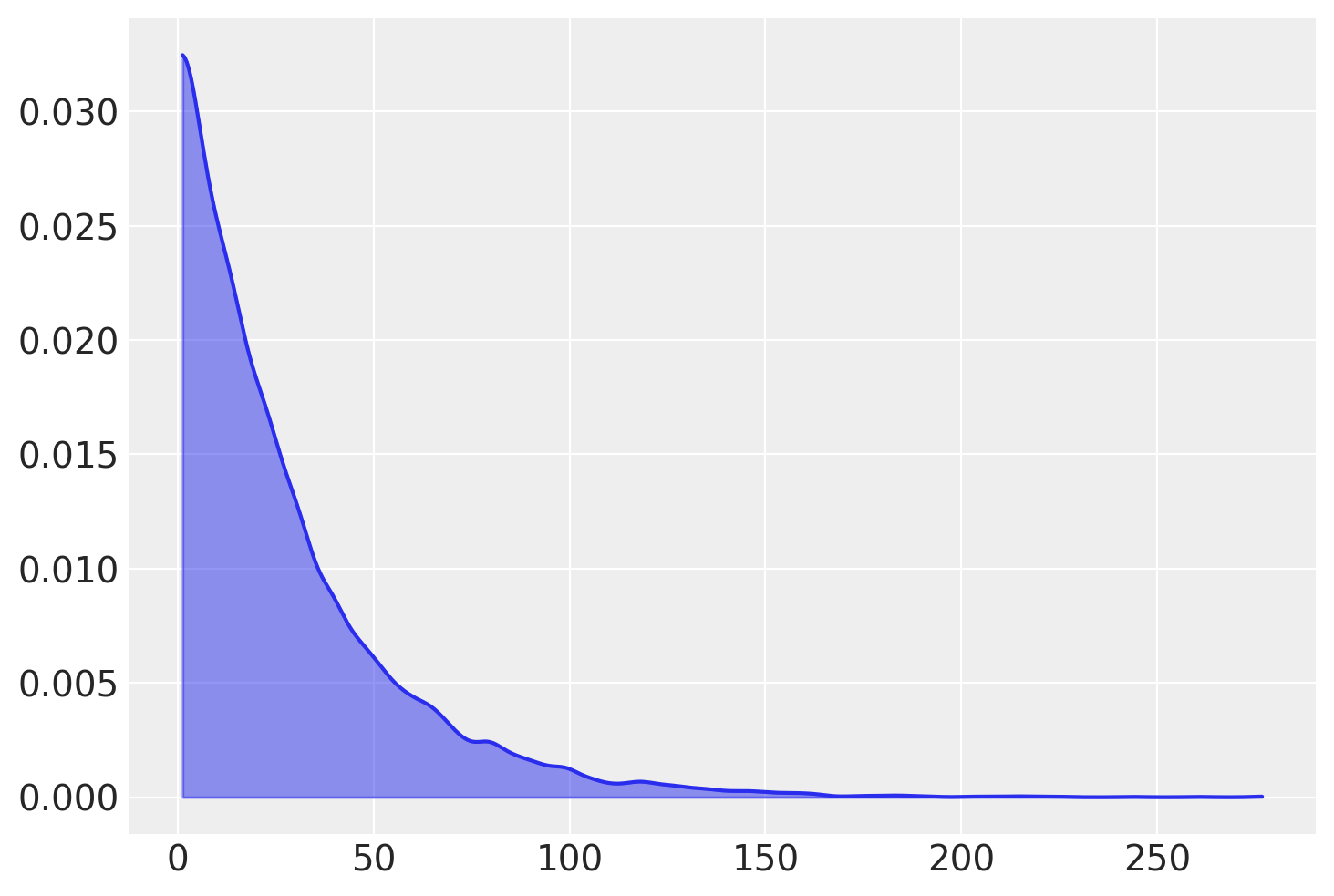
../../../_images/18e7bca44fe93e19cfb553969bcca2fe136f68f43e96c718c517f036df6395ab.png

由于 PyMC 以精度而不是标准差来参数化 Student-T 分布，因此我们必须先转换标准差，然后再指定我们的似然函数。

with model:
    lambda_1 = group1_std**-2
    lambda_2 = group2_std**-2
    group1 = pm.StudentT("drug", nu=nu, mu=group1_mean, lam=lambda_1, observed=iq_drug)
    group2 = pm.StudentT("placebo", nu=nu, mu=group2_mean, lam=lambda_2, observed=iq_placebo)

在完全指定了我们的概率模型之后，我们可以将注意力转向计算感兴趣的比较，以评估药物的效果。为此，我们可以在模型中指定确定性节点，用于表示组均值之间的差异和组标准差之间的差异。将它们包装在命名的 Deterministic 对象中，表示我们希望将采样值记录为输出的一部分。作为组的联合度量，我们还将估计“效应量”，即均值差异按合并标准差估计值缩放的结果。这个量可能更难解释，因为它不再与我们的数据单位相同，但这个量是所有四个估计参数的函数。

with model:
    diff_of_means = pm.Deterministic("difference of means", group1_mean - group2_mean)
    diff_of_stds = pm.Deterministic("difference of stds", group1_std - group2_std)
    effect_size = pm.Deterministic(
        "effect size", diff_of_means / np.sqrt((group1_std**2 + group2_std**2) / 2)
    )

现在，我们可以拟合模型并评估其输出。

with model:
    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [group1_mean, group2_mean, group1_std, group2_std, nu_minus_one]
100.00% [8000/8000 00:05<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 20 seconds.
The acceptance probability does not match the target. It is 0.8983, but should be close to 0.8. Try to increase the number of tuning steps.
The acceptance probability does not match the target. It is 0.8916, but should be close to 0.8. Try to increase the number of tuning steps.

我们可以绘制模型的随机参数。Arviz 的 plot_posterior 函数复制了 [Kruschke, 2013] 中描述的信息丰富的直方图。这些直方图总结了参数的后验分布，并展示了95%的可信区间和后验均值。下面的图表是使用每个链的最后1000个样本构建的，这些样本被合并在一起。

az.plot_posterior(
    idata,
    var_names=["group1_mean", "group2_mean", "group1_std", "group2_std", "nu", "nu_log10"],
    color="#87ceeb",
);
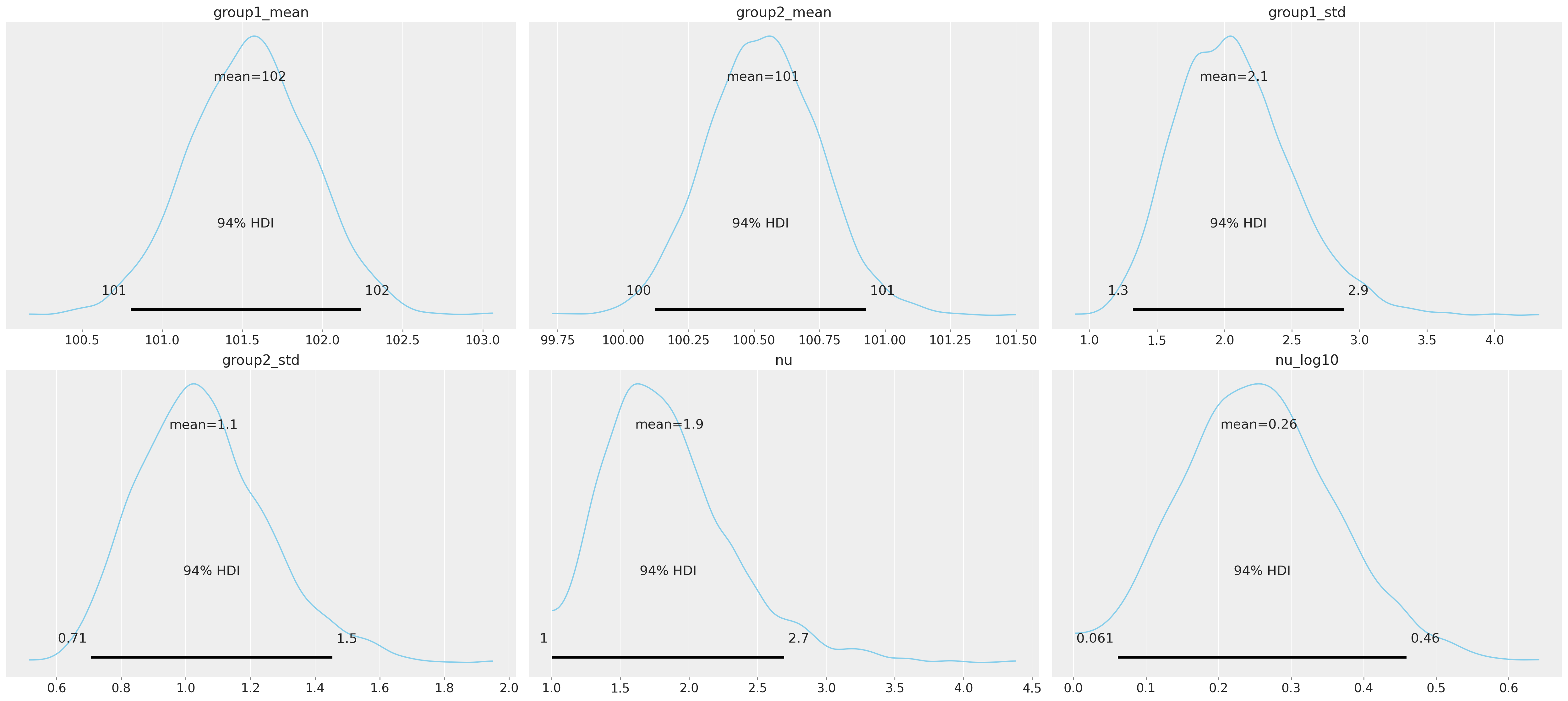
../../../_images/3d232f6e5768d7999646d15a2510af8129a95c0d2508cfd95cfded741d5875f0.png

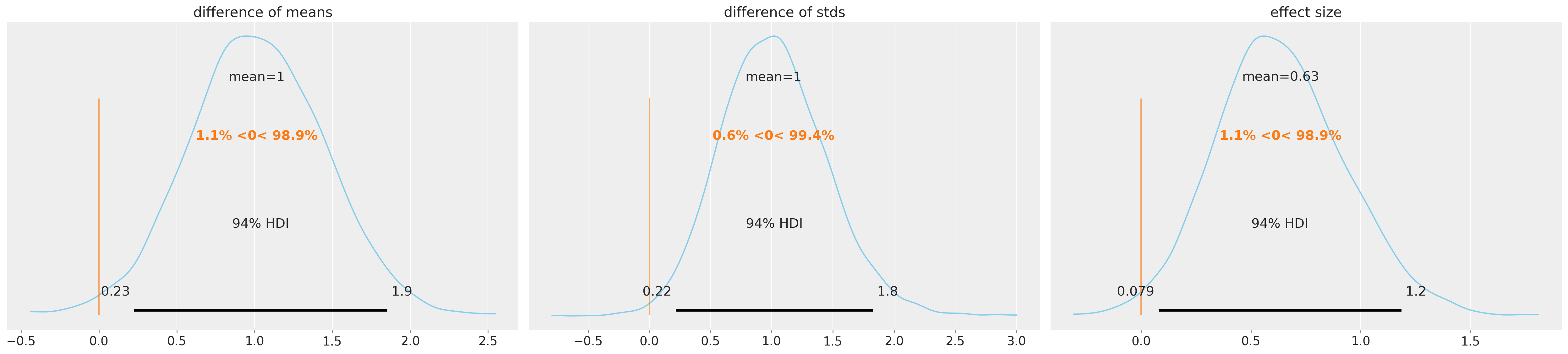
观察下面的组间差异，我们可以得出结论，在所有三个指标上，两组之间都存在有意义的差异。对于这些比较，使用零作为参考值（ref_val）是有用的；提供这个参考值可以得到后验分布在值两侧的累积概率。因此，对于均值差异，至少97%的后验概率大于零，这表明组均值可信地不同。效应量和标准差差异同样为正。

这些估计表明，“聪明药”不仅提高了预期分数，还增加了样本中分数的变异性。因此，这并不排除一些接受者可能受到药物的负面影响，而同时其他人受益的可能性。

az.plot_posterior(
    idata,
    var_names=["difference of means", "difference of stds", "effect size"],
    ref_val=0,
    color="#87ceeb",
);
../../../_images/dd0a6438e2cb2a0981f5f19e085a53f3cf7e0d2fba1ed7711a981b578e1c1515.png

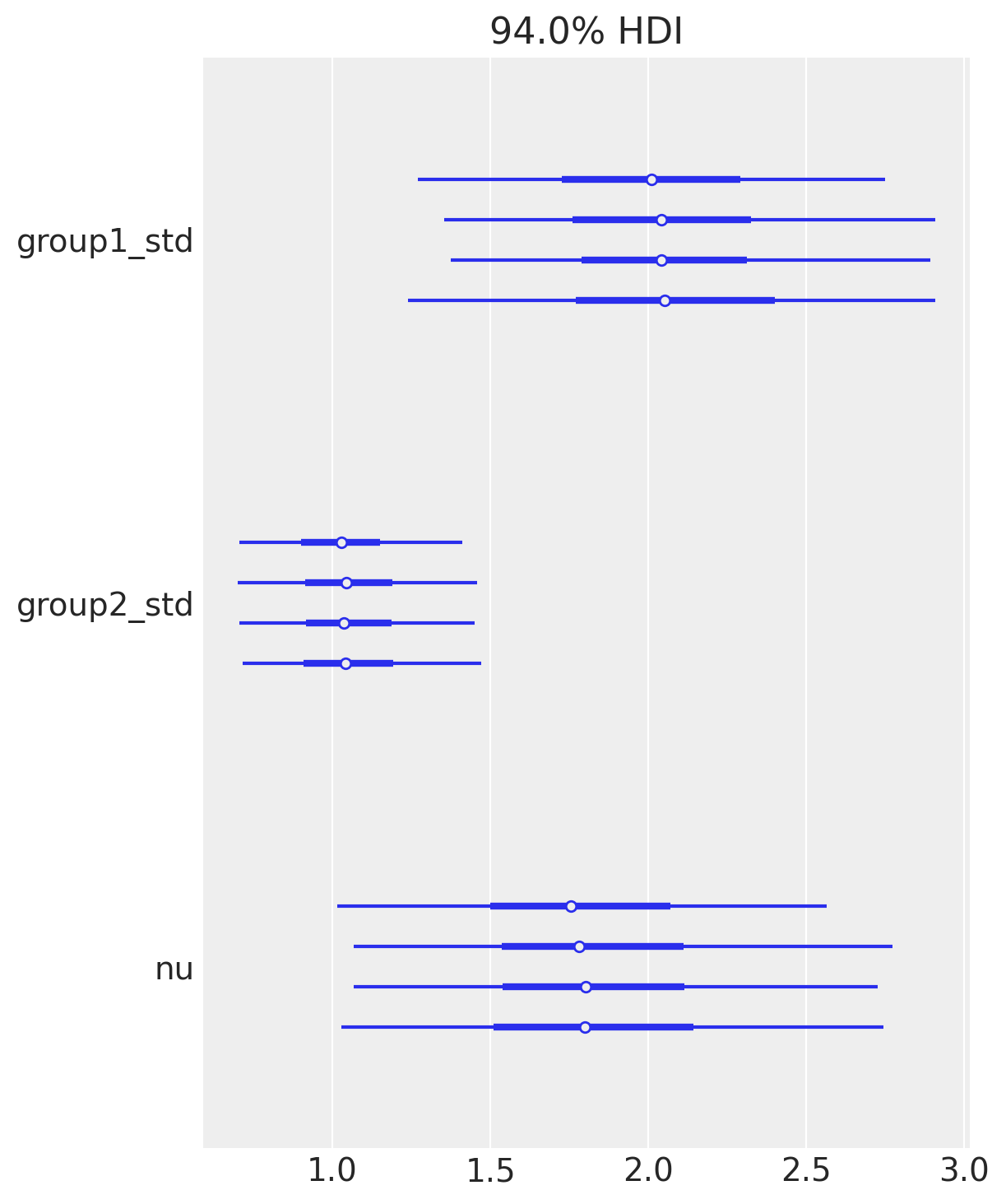
当在具有多个链的轨迹上调用plot_forest时，它还会绘制潜在尺度缩减参数，该参数用于揭示缺乏收敛性的证据；值接近1，正如我们在这里所看到的，表明模型已经收敛。

az.plot_forest(idata, var_names=["group1_mean", "group2_mean"]);
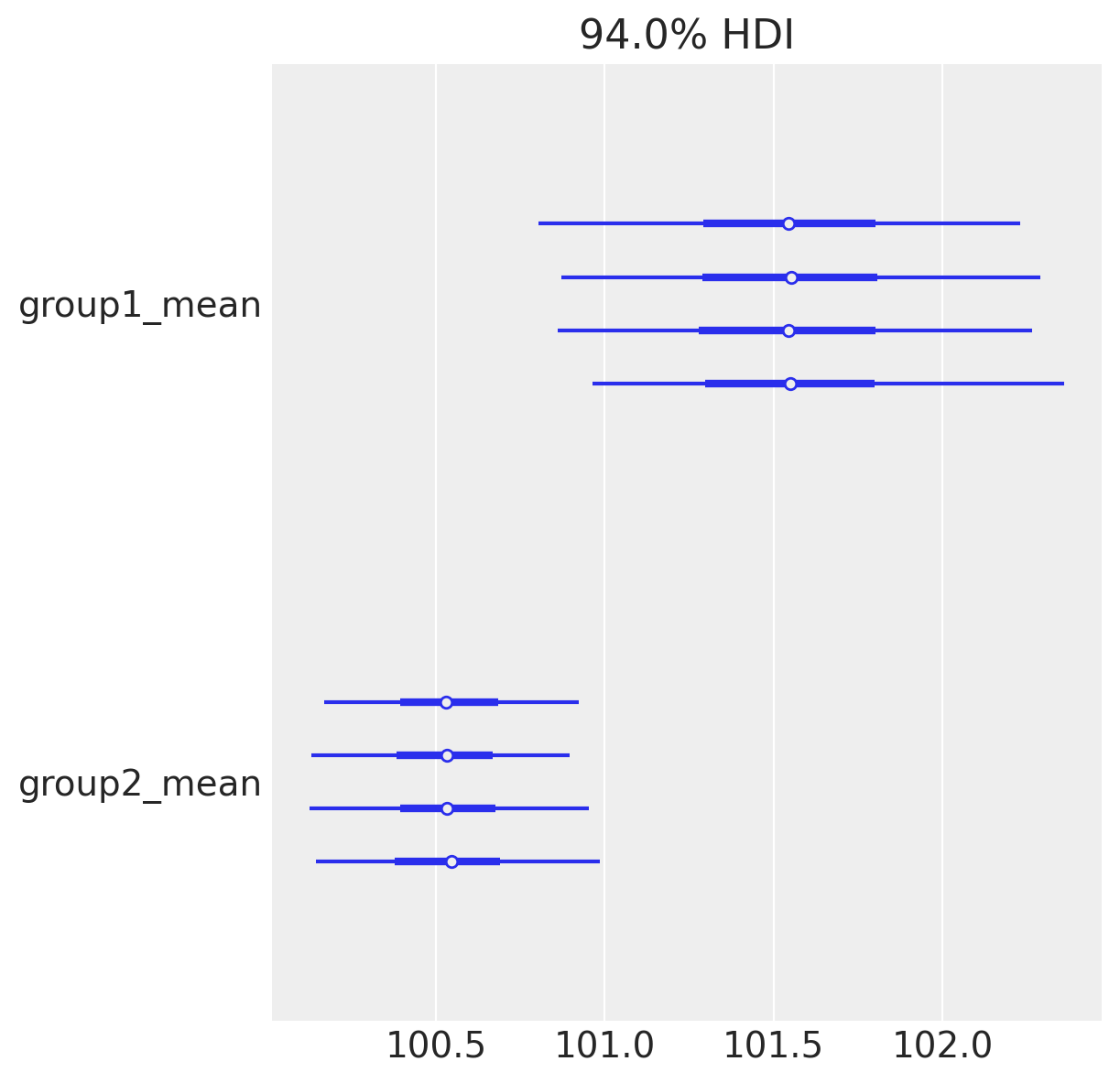
../../../_images/0d0c8870180c17d212d0b0322ad6cdfb3578564df8d7909923d28138021ecb37.png 
az.plot_forest(idata, var_names=["group1_std", "group2_std", "nu"]);
../../../_images/61708d09ba5a613503d3ef6aed87a9a1af5cce3278584aa15293175722f7dee4.png 
az.summary(idata, var_names=["difference of means", "difference of stds", "effect size"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
difference of means 1.014 0.436 0.225 1.854 0.007 0.005 3880.0 2915.0 1.0
difference of stds 1.015 0.435 0.218 1.828 0.007 0.005 3749.0 2876.0 1.0
effect size 0.635 0.295 0.079 1.185 0.005 0.003 4058.0 2577.0 1.0

作者身份#

  • 由Andrew Straw于2012年12月编写（best）

  • 由Thomas Wiecki在2015年移植到PyMC3

  • 由 Chris Fonnesbeck 于 2020 年 12 月更新

  • 由 Andrés Suárez 于 2022 年 1 月移植到 PyMC4（pymc-examples#52）

参考资料#

[1] (1,2,3)

约翰·K·克鲁施克. 贝叶斯估计取代t检验. 实验心理学杂志: 总论, 142(2):573–603, 2013. URL: https://doi.org/10.1037/a0029146, doi:10.1037/a0029146.

[2]

道格拉斯·H·约翰逊。统计显著性检验的无意义。《野生动物管理杂志》，63(3):763，1999年7月。URL: https://doi.org/10.2307/3802789, doi:10.2307/3802789.

[3]

Steven N. Goodman. 迈向循证医学统计学。1: p值谬误。内科学年鉴，130(12):995，1999年6月。URL: https://doi.org/10.7326/0003-4819-130-12-199906150-00008，doi:10.7326/0003-4819-130-12-199906150-00008。

水印#

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Wed Nov 09 2022

Python implementation: CPython
Python version       : 3.10.6
IPython version      : 8.5.0

numpy  : 1.23.4
seaborn: 0.12.0
arviz  : 0.13.0
pandas : 1.5.1
pymc   : 4.2.2

Watermark: 2.3.1