广义极值分布#

介绍#

广义极值（GEV）分布是一种包含Weibull、Gumbel和Frechet极值分布族的元分布。它用于建模平稳过程的极值（最大值或最小值）的分布，例如年最大风速、桥梁上年最大卡车重量等，而无需事先决定尾部行为。

遵循Coles [2001]中使用的参数化方法，极值分布（GEV）用于最大值的分布如下：

\[G(x) = \exp \left\{ \left[ 1 - \xi \left( \frac{x - \mu}{\sigma} \right) \right]^{-\frac{1}{\xi}} \right\}\]

当：

  • \(\xi < 0\) 我们得到具有有界上尾的威布尔分布；

  • \(\xi = 0\)，在极限情况下，我们得到Gumbel分布，两端无界；

  • \(\xi > 0\)，我们得到Frechet分布，它在下尾部是有界的。

请注意，形状参数 \(\xi\) 的这种参数化与 SciPy 中使用的符号相反（在 SciPy 中它被表示为 c）。此外，通过研究数据负值的最大值分布，可以很容易地检查最小值的分布。

我们将使用Port Pirie年最高海平面数据的例子，该数据在Coles [2001]中使用，并与那里提出的频率论结果进行比较。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pymc_experimental.distributions as pmx
import pytensor.tensor as pt

from arviz.plots import plot_utils as azpu

数据#

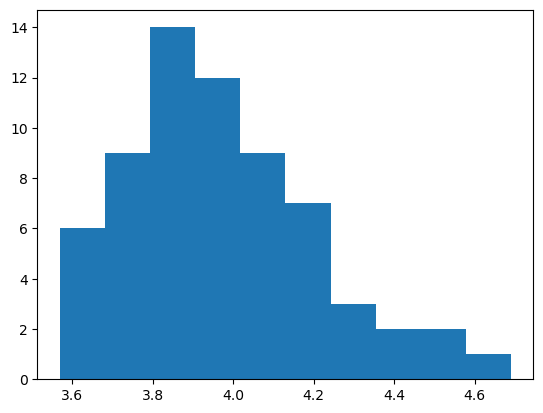
The Port Pirie数据由Coles [2001]提供，并在此重复：

# fmt: off
data = np.array([4.03, 3.83, 3.65, 3.88, 4.01, 4.08, 4.18, 3.80, 
                 4.36, 3.96, 3.98, 4.69, 3.85, 3.96, 3.85, 3.93, 
                 3.75, 3.63, 3.57, 4.25, 3.97, 4.05, 4.24, 4.22, 
                 3.73, 4.37, 4.06, 3.71, 3.96, 4.06, 4.55, 3.79, 
                 3.89, 4.11, 3.85, 3.86, 3.86, 4.21, 4.01, 4.11, 
                 4.24, 3.96, 4.21, 3.74, 3.85, 3.88, 3.66, 4.11, 
                 3.71, 4.18, 3.90, 3.78, 3.91, 3.72, 4.00, 3.66, 
                 3.62, 4.33, 4.55, 3.75, 4.08, 3.90, 3.88, 3.94, 
                 4.33])
# fmt: on
plt.hist(data)
plt.show()
../../../_images/a55604b4ac3c055cb349298ea8cfc1408df85a9882831a5bdbf9926cba81a45c.png

建模与预测#

在我们要进行的建模中，我们希望做两件事：

  • 基于一些相当非信息的先验，对GEV参数进行参数推断，并且；

  • 预测10年回报水平。

在贝叶斯框架下，考虑参数不确定性的极值预测很容易实现。有趣的是，将这种便利性与Caprani 和 OBrien [2010]在频率主义框架下进行此操作时遇到的困难进行比较。无论如何，在超过概率\(p\)下的预测值由以下公式给出：

\[ x_p = \mu - \frac{\sigma}{\xi} \left\{1 - \left[-\log\left(1-p\right)\right] \right\} \]

这是参数值的确定性函数，因此在模型上下文中使用pm.Deterministic来实现。

考虑10年回报期，其中 \(p = 1/10\)：

p = 1 / 10

现在使用从上述直方图的快速回顾中估计的先验设置模型：

  • \(\mu\): 除了标准差限制负结果的正态分布外，没有真正的依据考虑其他任何分布；

  • \(\sigma\): 这必须是正数，并且值很小，因此使用 HalfNormal 并设置单位标准差；

  • \(\xi\): 我们对尾部行为持不可知态度，因此将其中心设为零，但限制在物理上合理的范围内\(\pm 0.6\)，并使其在零附近保持一定程度的紧密性。

# Optionally centre the data, depending on fitting and divergences
# cdata = (data - data.mean())/data.std()

with pm.Model() as model:
    # Priors
    μ = pm.Normal("μ", mu=3.8, sigma=0.2)
    σ = pm.HalfNormal("σ", sigma=0.3)
    ξ = pm.TruncatedNormal("ξ", mu=0, sigma=0.2, lower=-0.6, upper=0.6)

    # Estimation
    gev = pmx.GenExtreme("gev", mu=μ, sigma=σ, xi=ξ, observed=data)
    # Return level
    z_p = pm.Deterministic("z_p", μ - σ / ξ * (1 - (-np.log(1 - p)) ** (-ξ)))

先验预测检查#

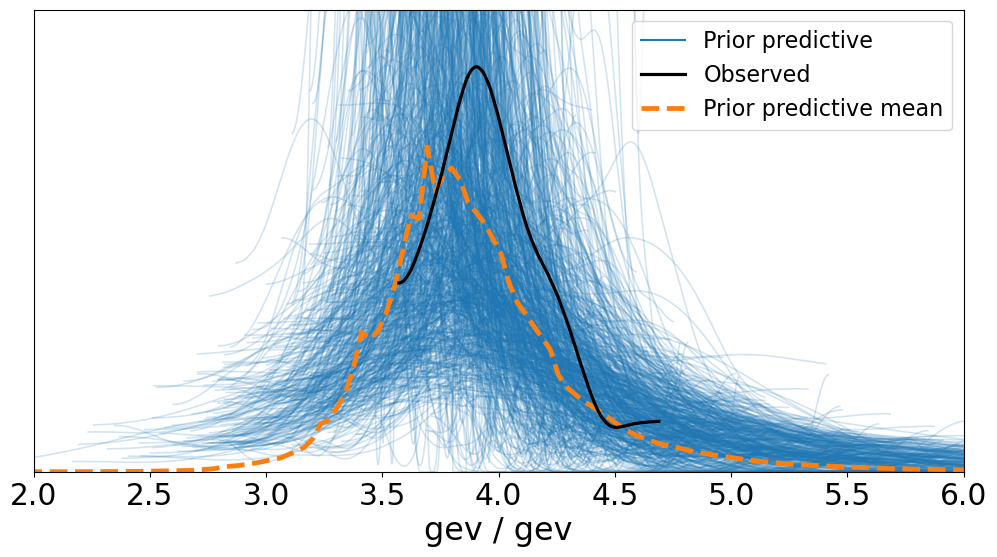
让我们感受一下我们选择的先验分布是否能覆盖数据的范围：

idata = pm.sample_prior_predictive(samples=1000, model=model)
az.plot_ppc(idata, group="prior", figsize=(12, 6))
ax = plt.gca()
ax.set_xlim([2, 6])
ax.set_ylim([0, 2]);

Sampling: [gev, μ, ξ, σ]
../../../_images/d770ff8bf19dc06fc365e39eaca0f302b3015348ed4c9ed9830fce6d6bdd3a22.png

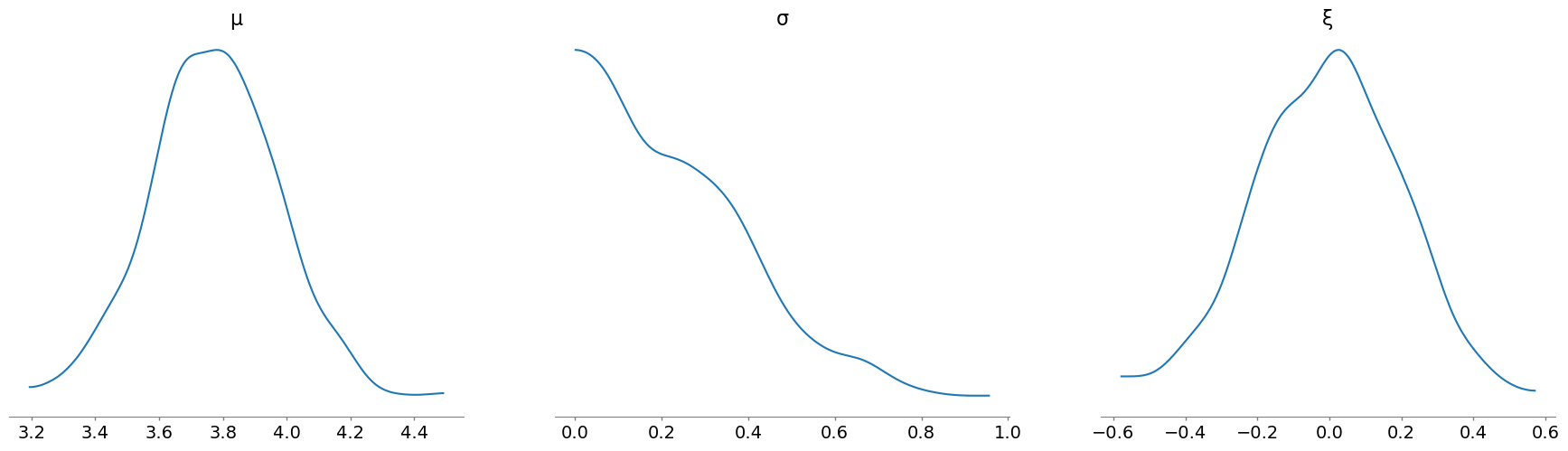
我们可以使用 plot_posterior 函数查看参数的采样值，但需要传入 idata 对象并指定 group 为 "prior"：

az.plot_posterior(
    idata, group="prior", var_names=["μ", "σ", "ξ"], hdi_prob="hide", point_estimate=None
);
../../../_images/3c79580c96d2862277463a3d417ac95a64b9724411ff59373cf5b515f1a07744.png

推理#

按下神奇的推理按钮\(^{\mathrm{TM}}\)：

with model:
    trace = pm.sample(
        5000,
        cores=4,
        chains=4,
        tune=2000,
        initvals={"μ": -0.5, "σ": 1.0, "ξ": -0.1},
        target_accept=0.98,
    )
# add trace to existing idata object
idata.extend(trace)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [μ, σ, ξ]
100.00% [28000/28000 00:15<00:00 Sampling 4 chains, 5 divergences] 
Sampling 4 chains for 2_000 tune and 5_000 draw iterations (8_000 + 20_000 draws total) took 16 seconds.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.

az.plot_trace(idata, var_names=["μ", "σ", "ξ"], figsize=(12, 12));
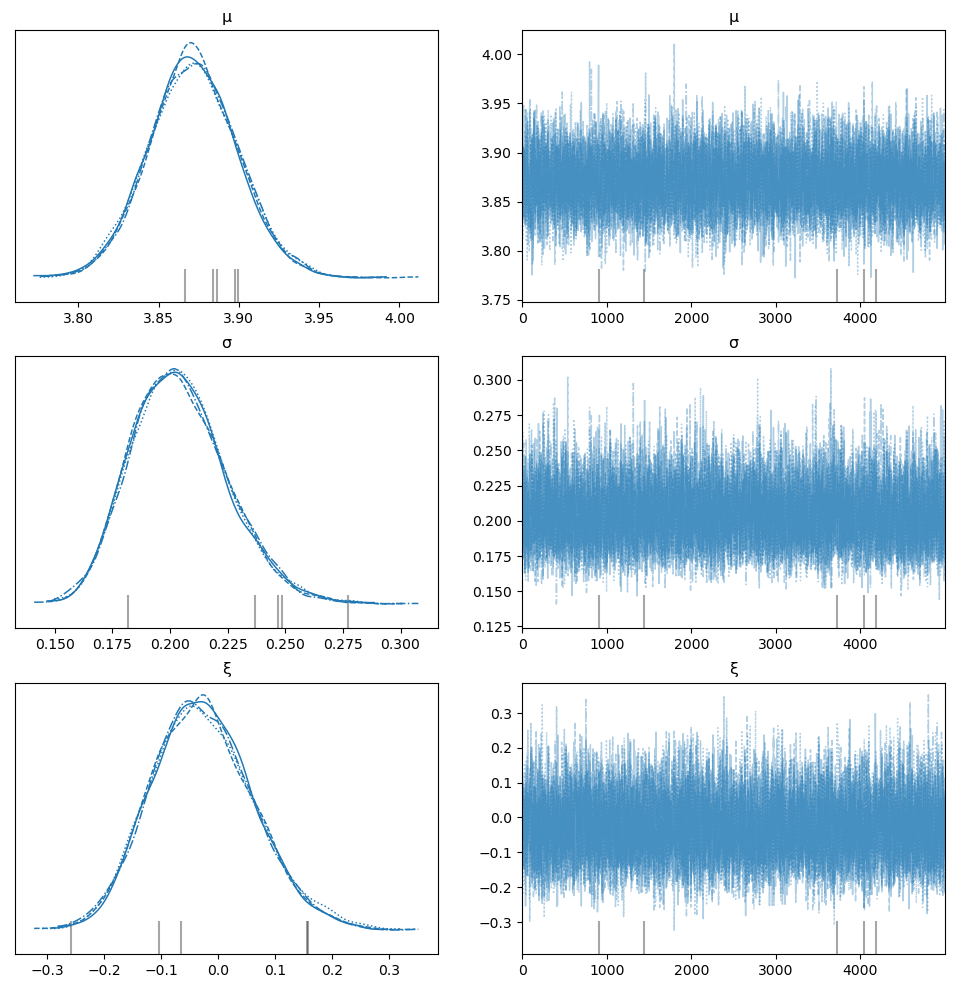
../../../_images/c4926cec91e25709902b64dced3b0bb3e809666e517a3699ea62464e5f116f79.png

分歧#

轨迹表现出分歧（通常情况下）。当参数的支持边界被接近时，HMC/NUTS采样器可能会出现问题。由于GEV的边界随着\(\xi\)的符号变化，因此很难提供一个解决此问题的变换。一种可能的变换——Box-Cox变换——由Bali [2003]提出，但Caprani和OBrien [2010]发现它在数值上不稳定，即使仅用于最大似然估计。无论如何，缓解分歧问题的建议是：

  • 增加目标接受率；

  • 使用更多信息丰富的先验，特别是将形状参数限制在物理上合理的值范围内，通常 \(\xi \in [-0.5,0.5]\)；

  • 确定尾部的吸引域（即Weibull、Gumbel或Frechet），并直接使用该分布。

推断#

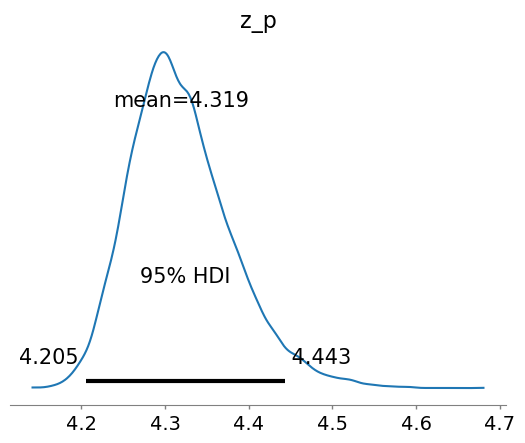
参数估计的95%可信区间范围是：

az.hdi(idata, hdi_prob=0.95)

<xarray.Dataset>
Dimensions:  (hdi: 2)
Coordinates:
  * hdi      (hdi) <U6 'lower' 'higher'
Data variables:
    μ        (hdi) float64 3.817 3.926
    σ        (hdi) float64 0.1668 0.2473
    ξ        (hdi) float64 -0.1989 0.1506
    z_p      (hdi) float64 4.205 4.443

并检查预测分布，考虑参数的可变性（且无需假设正态性）：

az.plot_posterior(idata, hdi_prob=0.95, var_names=["z_p"], round_to=4);
../../../_images/a3bb4510bf1e4b8f7ea412512a3869103d67e38c4263f898af48b143884b5cd5.png

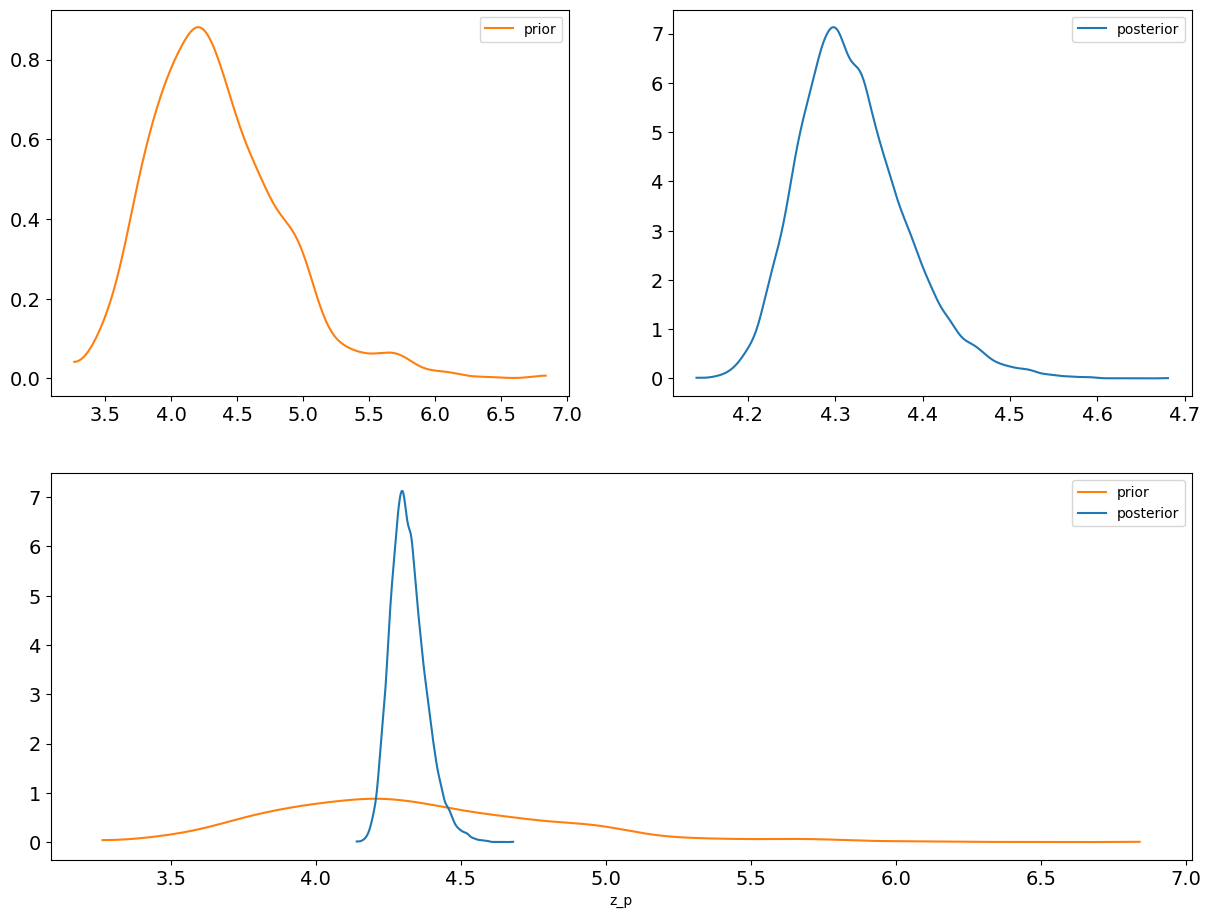
让我们比较先验和后验对 \(z_p\) 的预测，看看数据是如何影响这些预测的：

az.plot_dist_comparison(idata, var_names=["z_p"]);
../../../_images/d6a16b9417b6b2225f09e246d659a5c77eee2253e957f2fbb709f99d99ad7dfc.png

比较#

为了与Coles [2001]给出的结果进行比较，我们使用后验分布的模式（即最大后验或MAP估计）来近似最大似然估计（MLE）。当先验在后验估计附近合理平坦时，这些估计值接近。

在Coles [2001]中给出的最大似然估计结果是：

\[\left(\hat{\mu}, \hat{\sigma}, \hat{\xi} \right) = \left( 3.87, 0.198, -0.050 \right) \]

估计的方差-协方差矩阵为：

\[\begin{split} V = \left[ \begin{array} 0.000780 & 0.000197 & -0.00107 \\ 0.000197 & 0.000410 & -0.000778 \\ -0.00107 & -0.000778 & 0.00965 \end{array} \right] \end{split}\]

请注意，从我们的推理中提取最大似然估计（MLE）需要访问一些Arviz后端函数，以便将xarray转换为可检查的形式：

_, vals = az.sel_utils.xarray_to_ndarray(idata["posterior"], var_names=["μ", "σ", "ξ"])
mle = [azpu.calculate_point_estimate("mode", val) for val in vals]
mle

[3.87076953741271, 0.20235860610945772, -0.03389174278155249]

idata["posterior"].drop_vars("z_p").to_dataframe().cov().round(6)
μ σ ξ
μ 0.000771 0.000174 -0.000797
σ 0.000174 0.000436 -0.000562
ξ -0.000797 -0.000562 0.008051

结果非常吻合，但在贝叶斯框架下进行这一操作的好处是，我们可以免费获得参数和回报水平的完整后验联合分布。相比之下，在Coles [2001]中，即使是为了获得方差-协方差矩阵，也需要做出宽松的正态性假设并付出大量的计算努力。

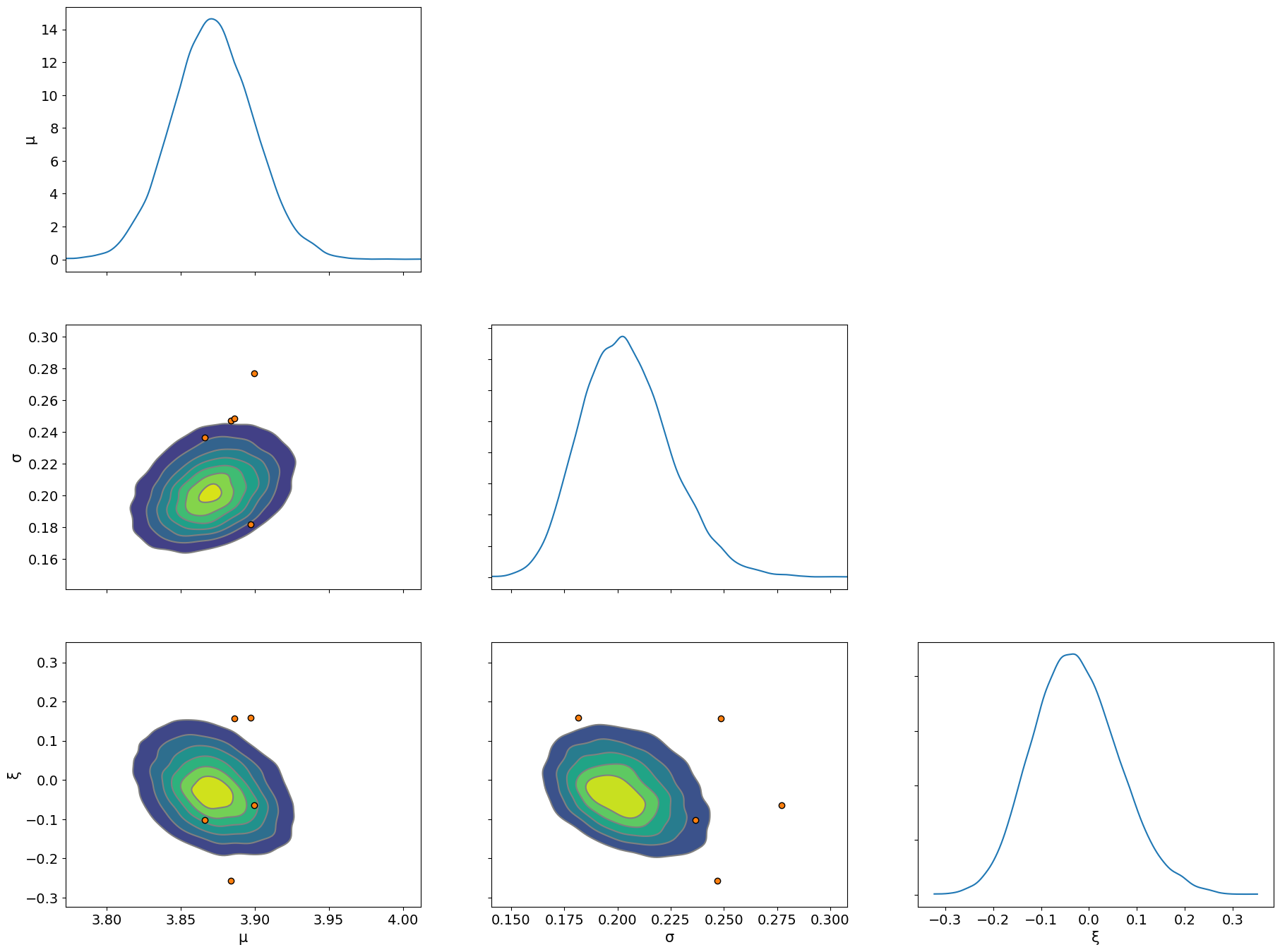
最后，我们检查配对图，并使用散度查看推断中存在的任何困难

az.plot_pair(idata, var_names=["μ", "σ", "ξ"], kind="kde", marginals=True, divergences=True);
../../../_images/5d67ffaa01c24dd8d61bbfd278293858c7ccb483126e006f40cf19617e183391.png

作者#

参考资料#

[1] (1,2,3,4,5,6)

斯图尔特·科尔斯。极值统计建模导论。统计学中的斯普林格系列。斯普林格，伦敦，英格兰，2001年8月，2001年版。ISBN 978-1-85233-459-8。URL: https://doi.org/10.1007/978-1-4471-3675-0.

[2]

Colin C. Caprani 和 Eugene J. OBrien。使用预测似然法估计极端桥梁交通荷载效应的分布。结构安全，32(2):138–144, 2010。URL: https://www.sciencedirect.com/science/article/pii/S016747300900071X, doi:https://doi.org/10.1016/j.strusafe.2009.09.001.

[3]

Turan G. Bali. 广义极值分布。经济学快报，79(3):423–427, 2003. URL: https://www.sciencedirect.com/science/article/pii/S0165176503000351, doi:https://doi.org/10.1016/S0165-1765(03)00035-1.

[4]

Colin C. Caprani 和 Eugene J. OBrien. 估计极端公路桥梁交通荷载效应。在 Hitoshi Furuta、Dan M Frangopol 和 Masanobu Shinozuka 编辑的 第十届国际结构安全与可靠性会议 (ICOSSAR2009) 论文集 中，1 – 8. CRC Press, 2010. URL: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.722.6789&rep=rep1&type=pdf.

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,arviz

Last updated: Tue Sep 27 2022

Python implementation: CPython
Python version       : 3.10.6
IPython version      : 8.5.0

pytensor: 2.8.6
arviz : 0.12.1

pymc_experimental: 0.0.1
sys              : 3.10.6 | packaged by conda-forge | (main, Aug 22 2022, 20:36:39) [GCC 10.4.0]
matplotlib       : 3.6.0
arviz            : 0.12.1
numpy            : 1.23.3
json             : 2.0.9
pytensor           : 2.8.6
pymc             : 3.9.3+1493.g372d7c24

Watermark: 2.3.1