从尴尬的分箱数据中估计分布的参数

问题

让我们假设我们对推断一个群体的属性感兴趣。这可以是任何东西，从年龄、收入或体重指数的分布，到各种可能的测量范围。在完成这项任务时，我们可能会经常遇到这样的情况：我们拥有多个数据集，每个数据集都可以提供关于总体群体的信息。

通常情况下，这些数据可能并不是我们作为数据科学家所认为的理想形式。例如，这些数据可能已经被分箱到类别中。这种做法不理想的一个原因是，分箱过程实际上会丢弃信息——我们失去了关于某个数据点在特定箱中的位置的任何知识。另一个不理想的原因是，不同的研究可能使用不同的分箱方法——例如，一项研究可能以十年为单位记录年龄（例如，某人是否在20多岁、30多岁、40多岁等），而另一项研究可能通过分配代际标签（如Z世代、千禧一代、X世代、婴儿潮二代、婴儿潮一代、战后一代）来间接记录年龄。

因此，我们面临一个问题：我们拥有包含我们感兴趣的测量值（无论是年龄、收入、BMI还是其他）的计数数据集，但这些数据是分箱的，并且它们已经被不同地分箱。本笔记本介绍了一个解决方案，这是由PyMC Labs在Gates Foundation的支持下开发的。我们可以对总体分布的参数进行推断。

解决方案

更正式地，我们将问题描述为：如果我们有用于数据分箱的箱边缘（即切割点）和箱计数，我们如何估计潜在分布的参数？我们将提出一个解决方案，并展示该解决方案的各种说明性示例，这些示例基于以下假设：

1. 这些分类是可排序的（例如：体重过轻、正常、超重、肥胖），

2. 底层分布以参数形式指定，并且

3. 划分区间的切点是已知的，并且可以在分布的支持上精确定位（也称为概率分布可以返回的有效值）。

使用的方法很大程度上基于序数回归背后的逻辑。该方法提出，观察到的区间计数 \(Y = {1, 2, \ldots, K}\) 是由一组区间边缘（也称为切点）\(\theta_1, \ldots, \theta _{K-1}\) 作用于一个潜在的概率分布生成的，我们可以称之为 \(y^*\)。我们可以将观察到数据在区间1中的概率描述为：

\[P(Y=1) = \Phi(\theta_1) - \Phi(-\infty) = \Phi(\theta_1) - 0\]

bin 2 为：

\[P(Y=2) = \Phi(\theta_2) - \Phi(\theta_1)\]

将第3个区间表示为：

\[P(Y=3) = \Phi(\theta_3) - \Phi(\theta_2)\]

并将第4个区间表示为：

\[P(Y=4) = \Phi(\infty) - \Phi(\theta_3) = 1 - \Phi(\theta_3)\]

其中 \(\Phi\) 是标准累积正态分布。

在序数回归中，切点被视为潜在变量，正态分布的参数可以被视为观测值（或从其他预测变量中得出）。这个问题与以下情况不同：

• 高斯分布的参数是未知的，

• 我们不希望局限于高斯分布，

• 我们观察到了一组cutpoints，

• 我们已经观察到bin counts，

我们现在可以勾勒出一个生成性的PyMC模型：

import pytensor.tensor as pt

with pm.Model() as model:
    # priors
    mu = pm.Normal("mu")
    sigma = pm.HalfNormal("sigma")
    # generative process
    probs = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), cutpoints))
    probs = pm.math.concatenate([[0], probs, [1]])
    probs = pt.extra_ops.diff(probs)
    # likelihood
    pm.Multinomial("counts", p=probs, n=sum(counts), observed=counts)

我们实现下面模型的具体方式与此仅有非常细微的差别，但让我们分解一下它是如何工作的。 首先，我们定义了潜在分布的mu和sigma参数的先验。然后我们有3行代码，用于计算任何观测数据落入给定区间的概率。这段代码的第一行

probs = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), cutpoints))

计算每个分位点的累积密度。第二行

probs = pm.math.concatenate([[0], probs, [1]])

简单地将累积密度在 \(-\infty\)（即零）和在 \(\infty\)（即1）处的值连接起来。 第三行

probs = pt.extra_ops.diff(probs)

计算连续累积密度之间的差异，以给出数据落在任何给定区间内的实际概率。

最后，我们以多项式似然结束，它告诉我们给定一组箱子概率probs和总观测数sum(counts)时，观测到counts的可能性。

假设我们可以使用基础 Python 或 numpy 来描述生成过程。然而，这样做的缺点是梯度信息会丢失，因此使用保留梯度信息的数值库来完成这些操作，可以使这些操作被 MCMC 采样算法使用。

该方法通过高斯分布进行了说明，下面我们展示了一些使用高斯分布的实际示例。然而，该方法是通用的，在本笔记本的末尾，我们提供了一个演示，证明该方法确实可以扩展到非高斯分布。

import warnings

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns

warnings.filterwarnings(action="ignore", category=UserWarning)

%matplotlib inline
%config InlineBackend.figure_format = 'retina'
plt.rcParams.update({"font.size": 14})
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(1234)

具有高斯分布的模拟数据

前几个示例将基于两个假设的研究，这些研究测量了一个高斯分布的变量。每个研究都有自己的样本量，我们的任务是学习总体水平高斯分布的参数。第一个难题是数据已经被分箱。第二个难题是每个研究使用了不同的类别，也就是说，在这个数据分箱过程中使用了不同的切点。

在这种模拟方法中，我们将定义真实的总体水平参数为：

• true_mu: -2.0

• true_sigma: 2.0

我们的目标是在仅给出分箱计数和切点的情况下，恢复mu和sigma的值。

# Generate two different sets of random samples from the same Gaussian.
true_mu, true_sigma = -2, 2
x1 = rng.normal(loc=true_mu, scale=true_sigma, size=1500)
x2 = rng.normal(loc=true_mu, scale=true_sigma, size=2000)

这些研究使用了以下不同的分界点来进行数据分箱处理。

# First discretization (cutpoints)
d1 = np.array([-2.0, -1.0, 0.0, 1.0, 2.0])
# Second discretization (cutpoints)
d2 = np.array([-5.0, -3.5, -2.0, -0.5, 1.0, 2.5])

def data_to_bincounts(data, cutpoints):
    # categorise each datum into correct bin
    bins = np.digitize(data, bins=cutpoints)
    # bin counts
    counts = pd.DataFrame({"bins": bins}).groupby(by="bins")["bins"].agg("count")
    return counts


c1 = data_to_bincounts(x1, d1)
c2 = data_to_bincounts(x2, d2)

让我们在一个方便的图中可视化这一点。左侧列显示了基础数据和两个研究的切割点。右侧列显示了结果的区间计数。

fig, ax = plt.subplots(2, 2, figsize=(12, 8))

# First set of measurements
ax[0, 0].hist(x1, 50, alpha=0.5)

for cut in d1:
    ax[0, 0].axvline(cut, color="k", ls=":")

# Plot observed bin counts
c1.plot(kind="bar", ax=ax[0, 1], alpha=0.5)
ax[0, 1].set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax[0, 1].set(title="Study 1", xlabel="c1", ylabel="bin count")

# Second set of measuremsnts
ax[1, 0].hist(x2, 50, alpha=0.5)

for cut in d2:
    ax[1, 0].axvline(cut, color="k", ls=":")

# Plot observed bin counts
c2.plot(kind="bar", ax=ax[1, 1], alpha=0.5)
ax[1, 1].set_xticklabels([f"bin {n}" for n in range(len(c2))])
ax[1, 1].set(title="Study 2", xlabel="c2", ylabel="bin count")

# format axes
ax[0, 0].set(xlim=(-11, 5), xlabel="$x$", ylabel="observed frequency", title="Sample 1")
ax[1, 0].set(xlim=(-11, 5), xlabel="$x$", ylabel="observed frequency", title="Sample 2");

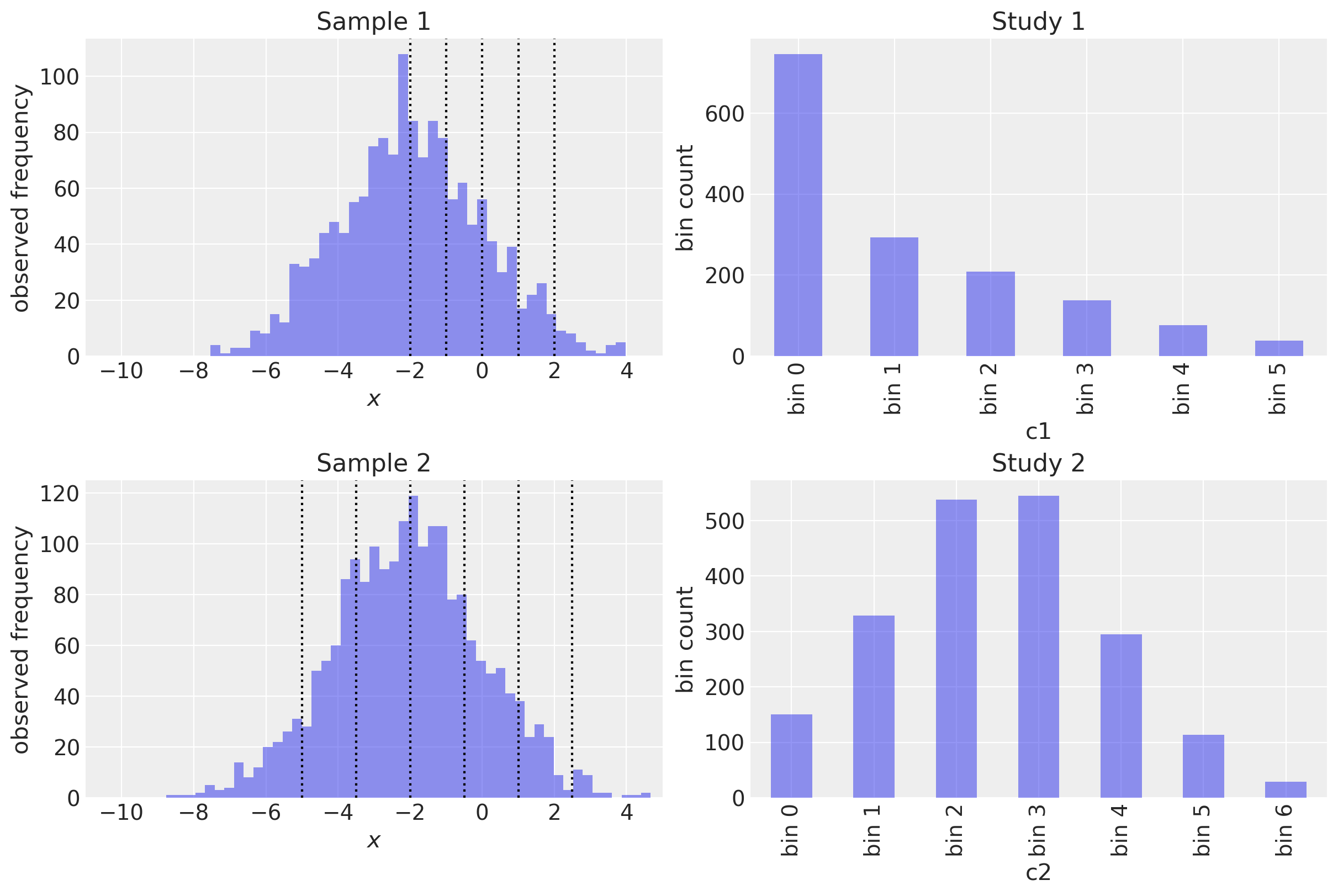
每个区间都与计数配对。 正如你将在上面看到的， c1 和 c2 被分成了不同的区间。 一个有6个区间，另一个有7个。 c1 基本上省略了一半的高斯分布。

回顾一下，在实际情况中，我们可能可以访问到切点（cutpoints）和分箱计数（bin counts），但无法访问到底层数据 x1 或 x2。

示例 1：使用一组区间进行高斯参数估计

我们将首先研究当我们仅使用一组箱子来估计mu和sigma参数时会发生什么。

模型规范

with pm.Model() as model1:
    sigma = pm.HalfNormal("sigma")
    mu = pm.Normal("mu")

    probs1 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([[0], probs1, [1]]))
    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values)

pm.model_to_graphviz(model1)

with model1:
    trace1 = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, mu]

100.00% [8000/8000 00:02<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 13 seconds.

模型检查

我们首先从后验预测检验开始。 给定后验值， 我们应该能够生成与我们所观察到的接近的观测值。

with model1:
    ppc = pm.sample_posterior_predictive(trace1)

100.00% [4000/4000 00:00<00:00]

我们可以通过图形方式来实现。

fig, ax = plt.subplots(figsize=(12, 4))
# Plot observed bin counts
c1.plot(kind="bar", ax=ax, alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(x="counts1_dim_0", y="counts1", color="k", alpha=0.2)
# Formatting
ax.set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax.set_title("Six bin discretization of N(-2, 2)")

Text(0.5, 1.0, 'Six bin discretization of N(-2, 2)')

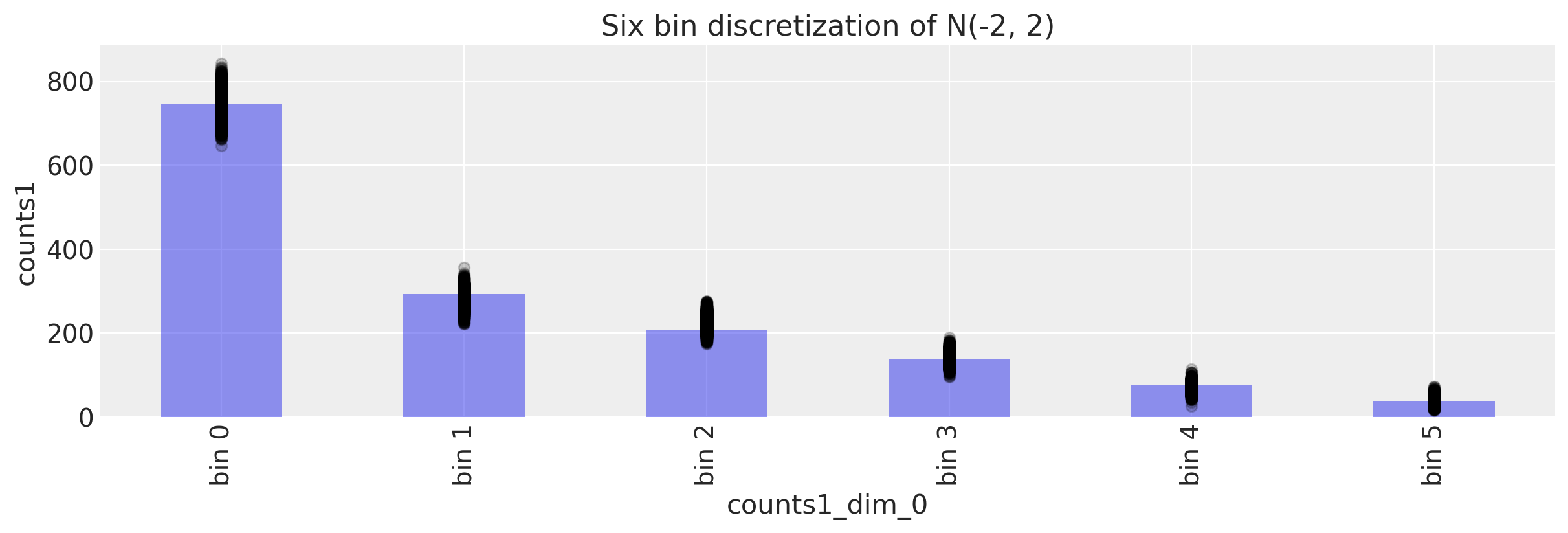
看起来这些数字在正确的范围内。 数字正确排序后，我们也正确识别了比例。

我们也可以通过多种方式以编程方式访问我们的后验预测：

ppc.posterior_predictive.counts1.values

array([[[714, 284, 228, 137,  74,  63],
        [753, 279, 228, 138,  66,  36],
        [734, 304, 222, 141,  60,  39],
        ...,
        [746, 274, 234, 127,  67,  52],
        [719, 290, 237, 150,  67,  37],
        [706, 285, 229, 143,  97,  40]],

       [[773, 263, 211, 149,  61,  43],
        [752, 253, 233, 153,  75,  34],
        [703, 294, 214, 148,  87,  54],
        ...,
        [686, 317, 257, 128,  66,  46],
        [758, 276, 240, 121,  66,  39],
        [755, 258, 221, 151,  62,  53]],

       [[796, 255, 181, 140,  74,  54],
        [764, 267, 224, 120,  83,  42],
        [794, 267, 196, 142,  65,  36],
        ...,
        [767, 263, 220, 129,  78,  43],
        [774, 278, 229, 125,  62,  32],
        [724, 289, 234, 153,  67,  33]],

       [[758, 284, 228, 126,  58,  46],
        [743, 274, 227, 145,  69,  42],
        [755, 299, 212, 119,  71,  44],
        ...,
        [718, 302, 240, 135,  68,  37],
        [722, 286, 217, 155,  78,  42],
        [767, 285, 201, 156,  67,  24]]])

让我们取平均值并与观察到的计数进行比较：

ppc.posterior_predictive.counts1.mean(dim=["chain", "draw"]).values

array([744.51325, 281.33575, 223.45975, 141.09875,  70.2235 ,  39.369  ])

c1.values

array([746, 293, 208, 138,  77,  38])

恢复参数

更重要的问題是我們是否已經恢復了分佈的參數。 回想起我們使用 mu = -2 和 sigma = 2 來生成數據。

az.plot_posterior(trace1, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma]);

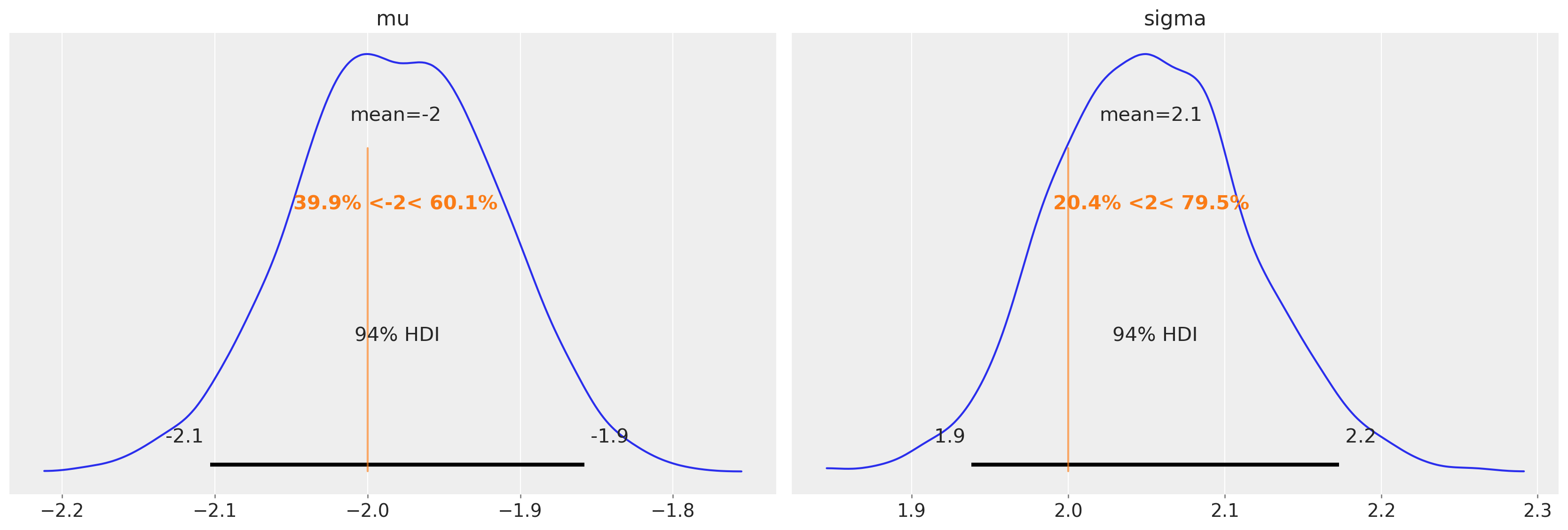
非常好！我们可以访问后验均值估计（存储为xarray类型），如下所示。MCMC样本以二维矩阵的形式返回，其中一个维度用于MCMC链（chain），另一个维度用于样本编号（draw）。我们可以使用.mean(dim=["draw", "chain"])计算总体后验平均值。

trace1.posterior["mu"].mean(dim=["draw", "chain"]).values

array(-1.98161385)

trace1.posterior["sigma"].mean(dim=["draw", "chain"]).values

array(2.05300289)

示例 2：使用另一组区间进行参数估计

上面，我们使用了一组分箱数据。让我们看看当我们换成另一组数据时会发生什么。

模型规范

与上述内容一样，这里是模型规范。

with pm.Model() as model2:
    sigma = pm.HalfNormal("sigma")
    mu = pm.Normal("mu")

    probs2 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), d2))
    probs2 = pt.extra_ops.diff(pm.math.concatenate([[0], probs2, [1]]))
    pm.Multinomial("counts2", p=probs2, n=c2.sum(), observed=c2.values)

with model2:
    trace2 = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, mu]

100.00% [8000/8000 00:01<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 11 seconds.

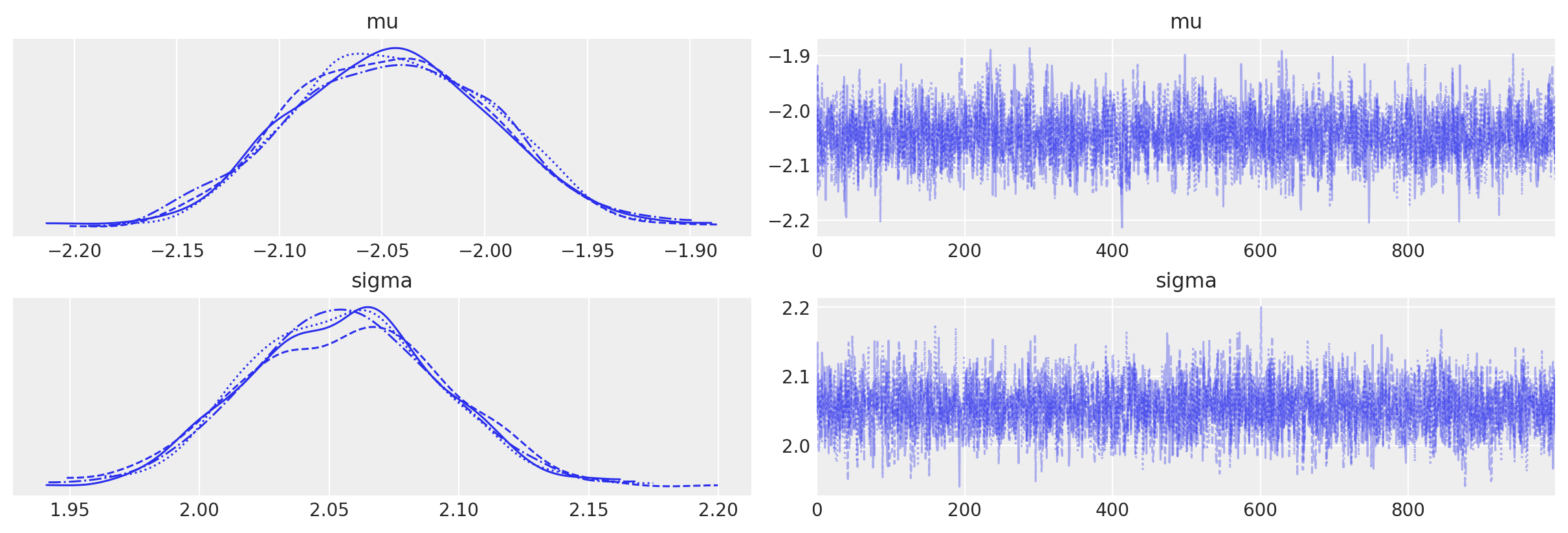
az.plot_trace(trace2);

后验预测检查

让我们运行一个PPC检查，以确保我们生成的数据与我们观察到的数据相似。

with model2:
    ppc = pm.sample_posterior_predictive(trace2)

100.00% [4000/4000 00:00<00:00]

我们计算平均样本后的均值区间后验预测区间计数。

ppc.posterior_predictive.counts2.mean(dim=["chain", "draw"]).values

array([150.6875 , 328.46925, 537.65775, 530.53625, 313.99   , 111.5935 ,
        27.06575])

c2.values

array([150, 329, 538, 545, 295, 114,  29])

看起来是一个很好的匹配。但一如既往，将事物可视化是明智的。

fig, ax = plt.subplots(figsize=(12, 4))
# Plot observed bin counts
c2.plot(kind="bar", ax=ax, alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(x="counts2_dim_0", y="counts2", color="k", alpha=0.2)
# Formatting
ax.set_xticklabels([f"bin {n}" for n in range(len(c2))])
ax.set_title("Seven bin discretization of N(-2, 2)")

Text(0.5, 1.0, 'Seven bin discretization of N(-2, 2)')

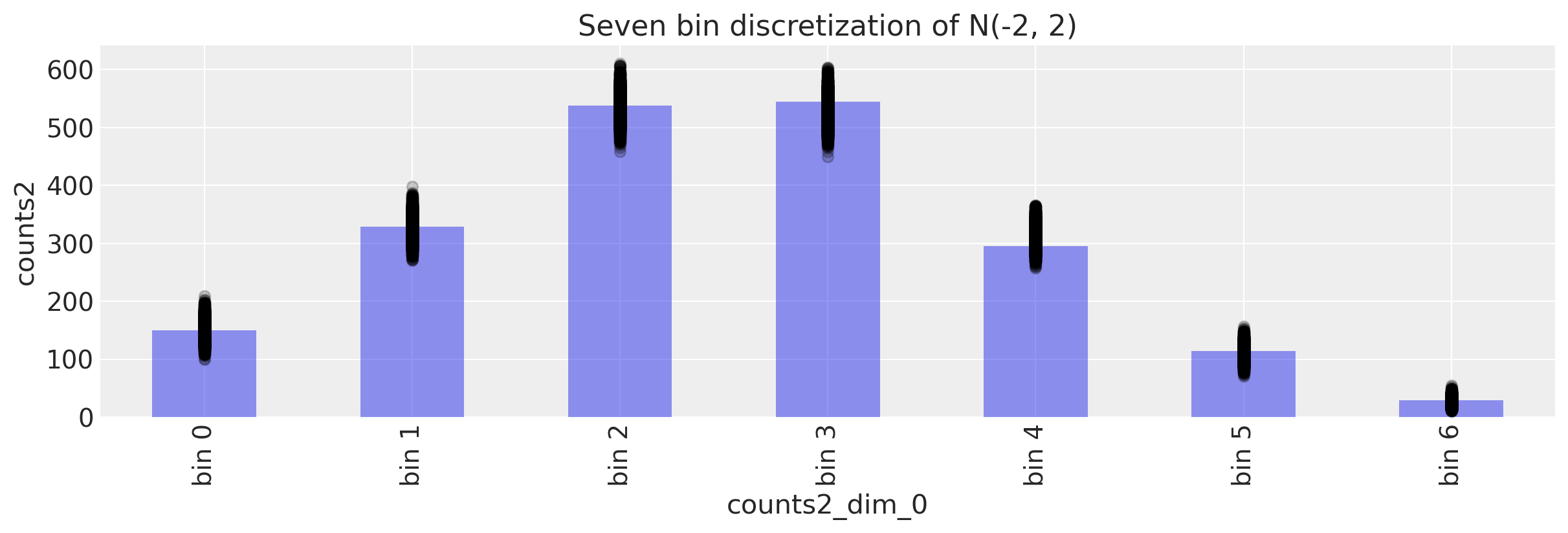
不错！

恢复参数

我们是否恢复了参数？

az.plot_posterior(trace2, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma]);

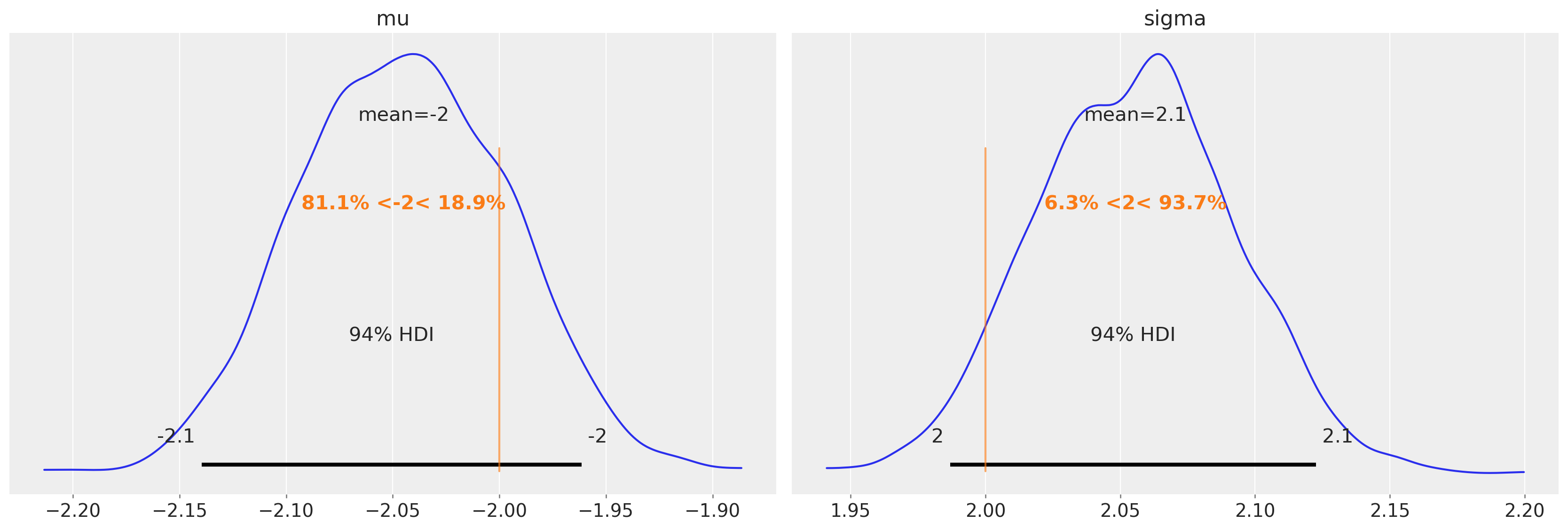
trace2.posterior["mu"].mean(dim=["draw", "chain"]).values

array(-2.04489232)

trace2.posterior["sigma"].mean(dim=["draw", "chain"]).values

array(2.05560527)

示例 3：两个区间一起的参数估计

现在我们需要看看如果我们同时使用两种分箱方式会发生什么。

模型规范

with pm.Model() as model3:
    sigma = pm.HalfNormal("sigma")
    mu = pm.Normal("mu")

    probs1 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs1, np.array([1])]))
    probs1 = pm.Deterministic("normal1_cdf", probs1)

    probs2 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), d2))
    probs2 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs2, np.array([1])]))
    probs2 = pm.Deterministic("normal2_cdf", probs2)

    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values)
    pm.Multinomial("counts2", p=probs2, n=c2.sum(), observed=c2.values)

pm.model_to_graphviz(model3)

with model3:
    trace3 = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, mu]

100.00% [8000/8000 00:02<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 13 seconds.

az.plot_pair(trace3, var_names=["mu", "sigma"], divergences=True);

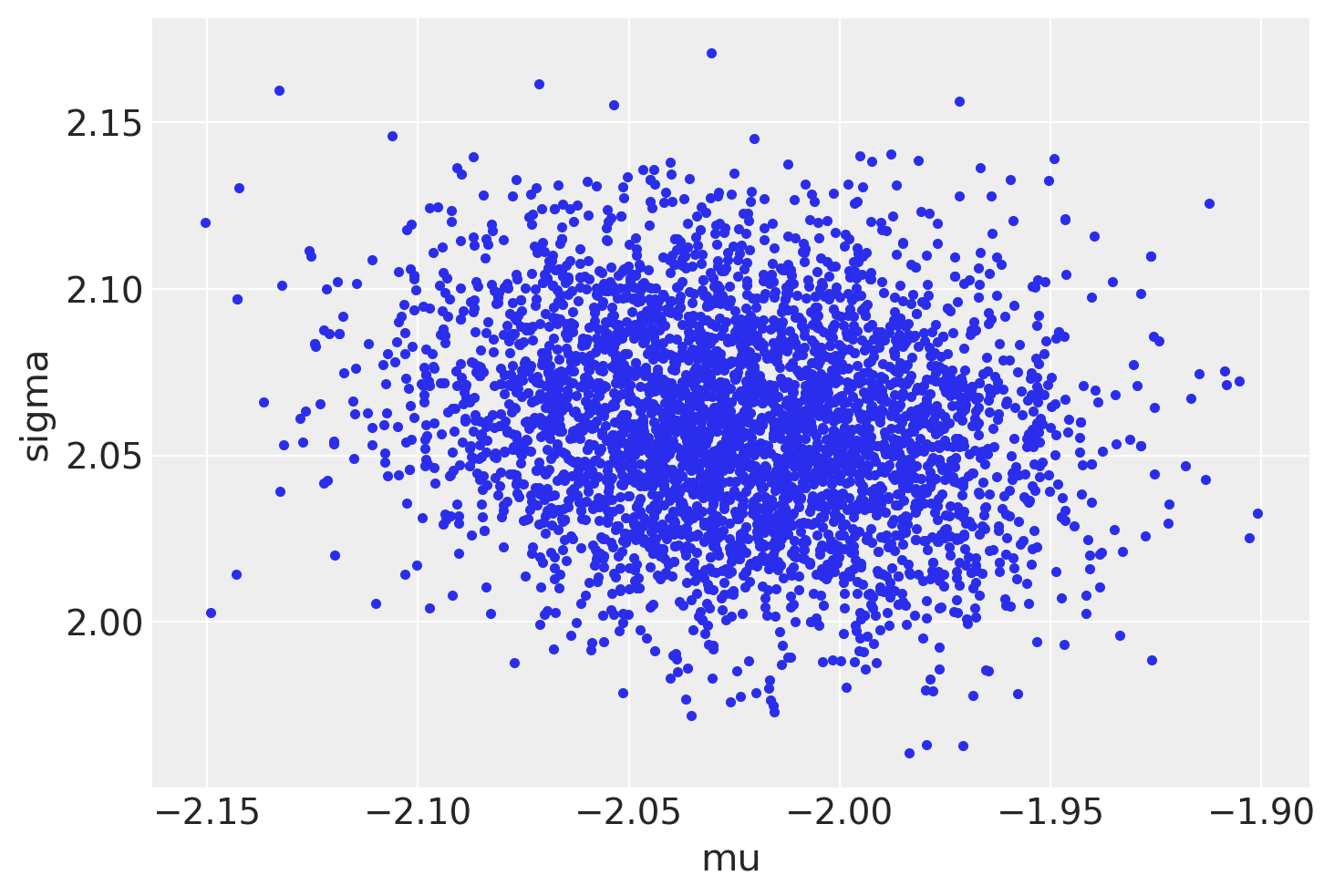
后验预测检查

with model3:
    ppc = pm.sample_posterior_predictive(trace3)

100.00% [4000/4000 00:00<00:00]

fig, ax = plt.subplots(1, 2, figsize=(12, 4), sharey=True)

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
c1.plot(kind="bar", ax=ax[0], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(
    x="counts1_dim_0", y="counts1", color="k", alpha=0.2, ax=ax[0]
)
# Formatting
ax[0].set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax[0].set_title("Six bin discretization of N(-2, 2)")

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
c2.plot(kind="bar", ax=ax[1], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(
    x="counts2_dim_0", y="counts2", color="k", alpha=0.2, ax=ax[1]
)
# Formatting
ax[1].set_xticklabels([f"bin {n}" for n in range(len(c2))])
ax[1].set_title("Seven bin discretization of N(-2, 2)")

Text(0.5, 1.0, 'Seven bin discretization of N(-2, 2)')

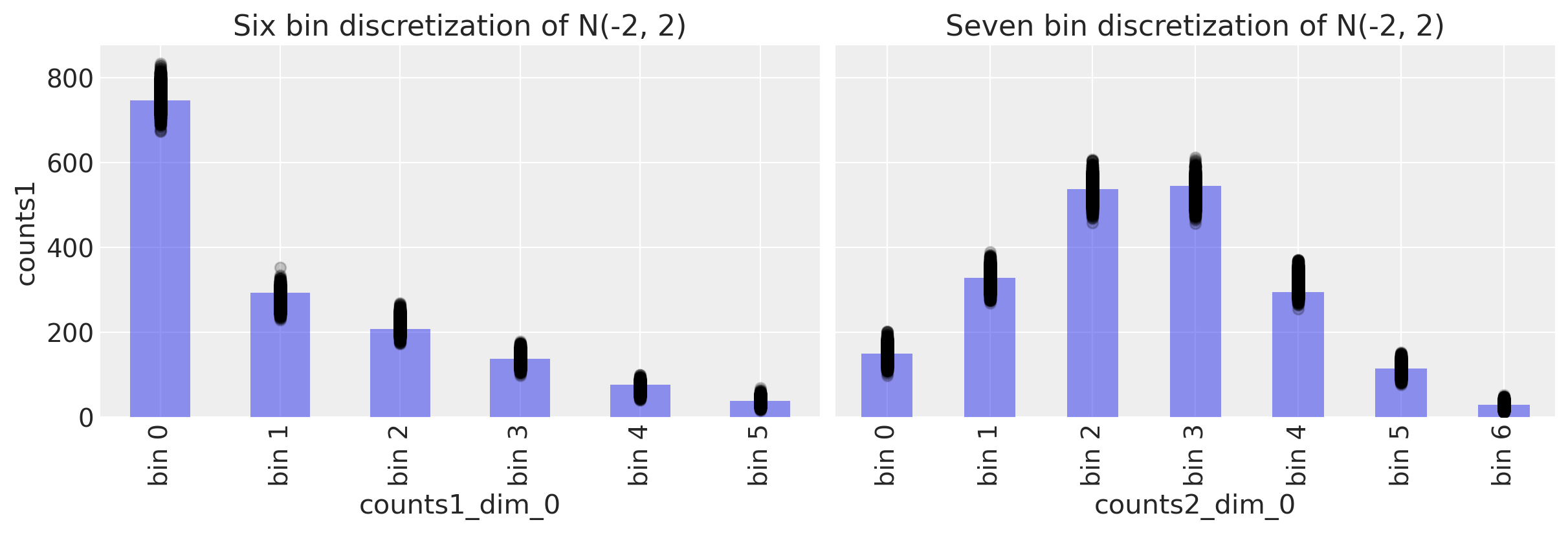
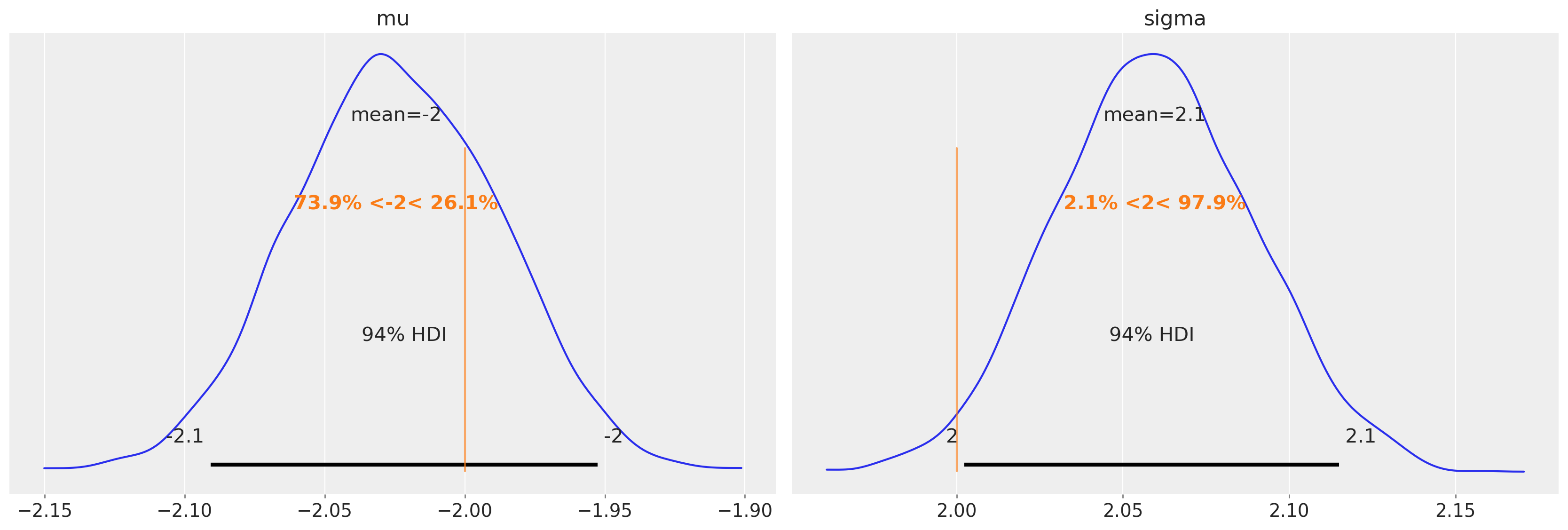
恢复参数

trace3.posterior["mu"].mean(dim=["draw", "chain"]).values

array(-2.02455161)

trace3.posterior["sigma"].mean(dim=["draw", "chain"]).values

array(2.05959445)

az.plot_posterior(trace3, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma]);

示例 4：使用连续和分箱测量的参数估计

为了完整性，让我们看看如何基于一组连续测量值和一组分箱测量值来估计总体参数。我们将使用我们已经生成的模拟数据。

模型规范

with pm.Model() as model4:
    sigma = pm.HalfNormal("sigma")
    mu = pm.Normal("mu")
    # study 1
    probs1 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu, sigma=sigma), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs1, np.array([1])]))
    probs1 = pm.Deterministic("normal1_cdf", probs1)
    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values)
    # study 2
    pm.Normal("y", mu=mu, sigma=sigma, observed=x2)

pm.model_to_graphviz(model4)

with model4:
    trace4 = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [sigma, mu]

100.00% [8000/8000 00:02<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 12 seconds.

后验预测检查

with model4:
    ppc = pm.sample_posterior_predictive(trace4)

100.00% [4000/4000 00:00<00:00]

fig, ax = plt.subplots(1, 2, figsize=(12, 4))

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
c1.plot(kind="bar", ax=ax[0], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(
    x="counts1_dim_0", y="counts1", color="k", alpha=0.2, ax=ax[0]
)
# Formatting
ax[0].set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax[0].set_title("Posterior predictive: Study 1")

# Study 2 ----------------------------------------------------------------
ax[1].hist(ppc.posterior_predictive.y.values.flatten(), 50, density=True, alpha=0.5)
ax[1].set(title="Posterior predictive: Study 2", xlabel="$x$", ylabel="density");

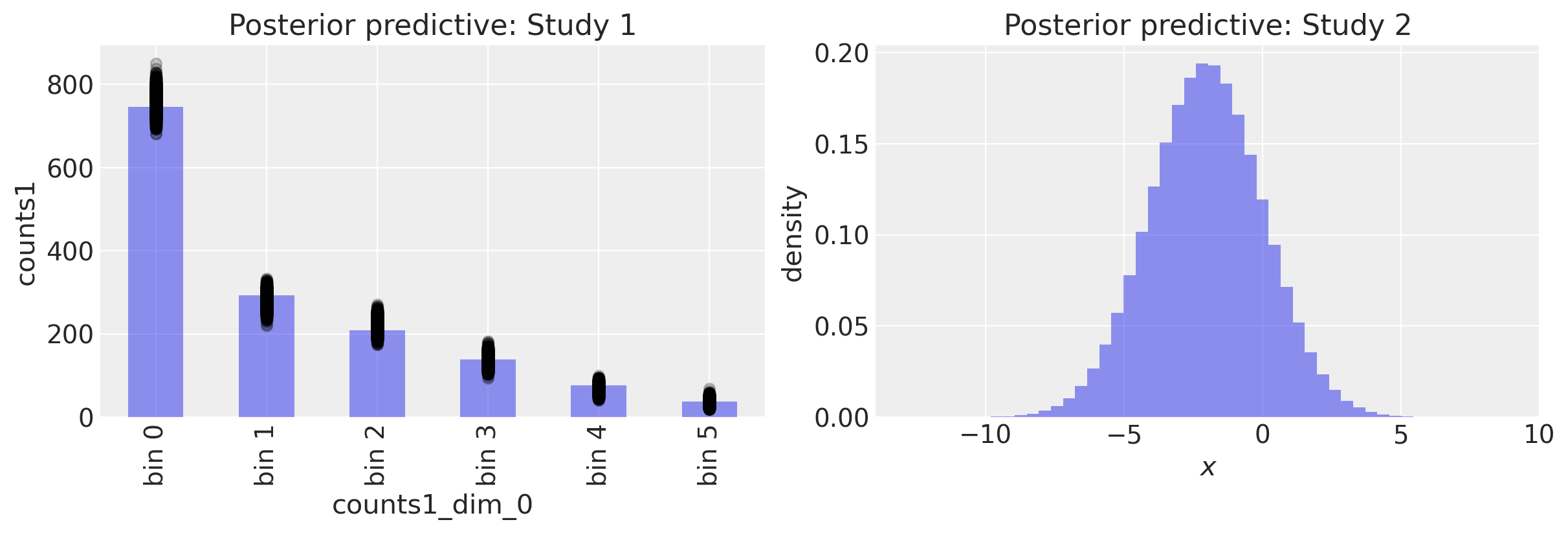
我们可以计算研究2的后验预测分布的均值和标准差，并发现它们接近我们的真实参数。

np.mean(ppc.posterior_predictive.y.values.flatten()), np.std(
    ppc.posterior_predictive.y.values.flatten()
)

(-2.030965696788321, 2.0470152029638515)

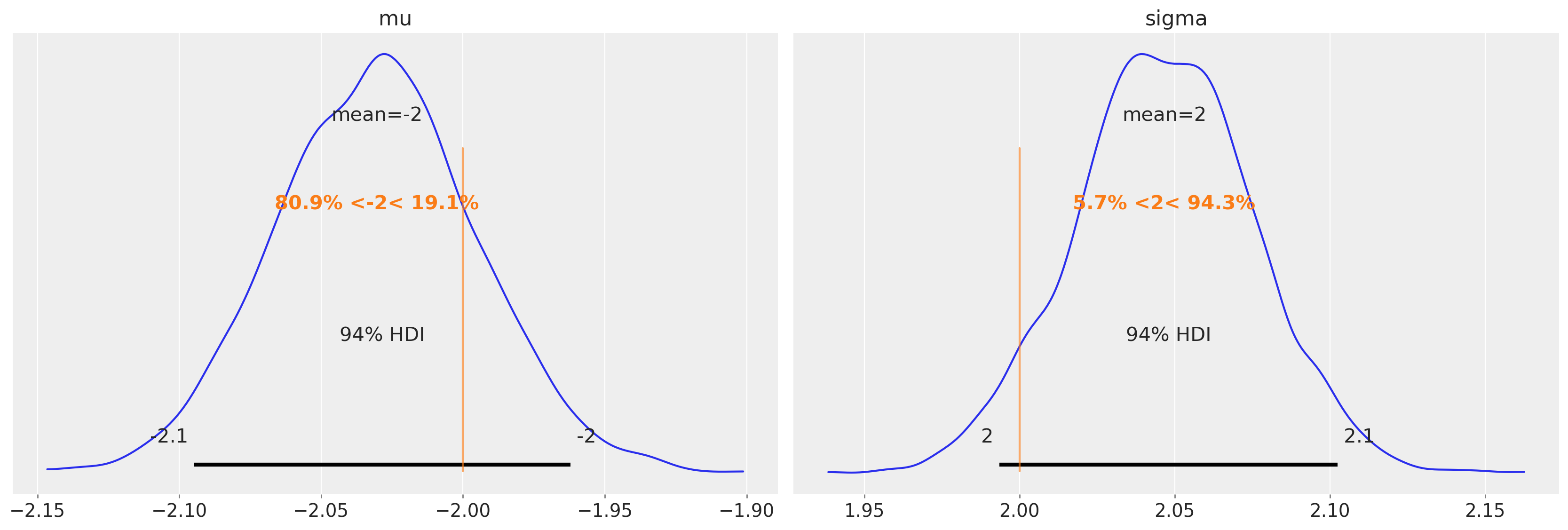
恢复参数

最后，我们可以检查参数的后验估计，并看到这里的估计非常准确。

az.plot_posterior(trace4, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma]);

示例 5：分层估计

前面的例子都假设研究1和研究2的数据是从同一个总体中抽取的。虽然这对于我们模拟的数据来说是正确的，但当我们处理真实数据时，我们无法确定这一点。因此，能够提出这样的问题可能是有用的：“研究1和研究2的数据是否看起来像是来自同一个总体？”

我们可以使用相同的基本方法来实现这一点——我们可以像之前一样估计总体水平的参数，但现在我们可以在其中加入研究水平的参数估计。这将在我们的模型中在总体水平参数和观测值之间增加一个新的层次结构层。

模型规范

这次，因为我们正在进入一个更复杂的模型，我们将使用 coords 来告诉 PyMC 变量的维度。这会输入到以 xarray 格式输出的后验样本中，这使得在后续进行统计分析或可视化处理时更加方便。

coords = {
    "study": np.array([0, 1]),
    "bin1": np.arange(len(c1)),
    "bin2": np.arange(len(c2)),
}

with pm.Model(coords=coords) as model5:
    # Population level priors
    mu_pop_mean = pm.Normal("mu_pop_mean", 0.0, 1.0)
    mu_pop_variance = pm.HalfNormal("mu_pop_variance", sigma=1)

    sigma_pop_mean = pm.HalfNormal("sigma_pop_mean", sigma=1)
    sigma_pop_sigma = pm.HalfNormal("sigma_pop_sigma", sigma=1)

    # Study level priors
    mu = pm.Normal("mu", mu=mu_pop_mean, sigma=mu_pop_variance, dims="study")
    sigma = pm.TruncatedNormal(
        "sigma", mu=sigma_pop_mean, sigma=sigma_pop_sigma, lower=0, dims="study"
    )

    # Study 1
    probs1 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu[0], sigma=sigma[0]), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs1, np.array([1])]))
    probs1 = pm.Deterministic("normal1_cdf", probs1, dims="bin1")

    # Study 2
    probs2 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu[1], sigma=sigma[1]), d2))
    probs2 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs2, np.array([1])]))
    probs2 = pm.Deterministic("normal2_cdf", probs2, dims="bin2")

    # Likelihood
    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values, dims="bin1")
    pm.Multinomial("counts2", p=probs2, n=c2.sum(), observed=c2.values, dims="bin2")

pm.model_to_graphviz(model5)

上述模型是不错的但直接运行这个模型会导致采样过程中出现数百次发散（你可以在诊断偏差推理与发散笔记本中了解更多关于发散的信息）。虽然我们不会在这里深入探讨原因，但简而言之，高斯中心化引入了一些病态到我们的对数似然空间中，使得MCMC采样器难以工作。首先，我们移除了sigma的群体水平估计，仅保留研究级别的先验。我们使用了Gamma分布来避免任何零值。其次，使用非中心化的重参数化来指定mu。这并不能完全解决问题，但它确实大大减少了发散的数量。

with pm.Model(coords=coords) as model5:
    # Population level priors
    mu_pop_mean = pm.Normal("mu_pop_mean", 0.0, 1.0)
    mu_pop_variance = pm.HalfNormal("mu_pop_variance", sigma=1)

    # Study level priors
    x = pm.Normal("x", dims="study")
    mu = pm.Deterministic("mu", x * mu_pop_variance + mu_pop_mean, dims="study")

    sigma = pm.Gamma("sigma", alpha=2, beta=1, dims="study")

    # Study 1
    probs1 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu[0], sigma=sigma[0]), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs1, np.array([1])]))
    probs1 = pm.Deterministic("normal1_cdf", probs1, dims="bin1")

    # Study 2
    probs2 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu[1], sigma=sigma[1]), d2))
    probs2 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs2, np.array([1])]))
    probs2 = pm.Deterministic("normal2_cdf", probs2, dims="bin2")

    # Likelihood
    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values, dims="bin1")
    pm.Multinomial("counts2", p=probs2, n=c2.sum(), observed=c2.values, dims="bin2")

pm.model_to_graphviz(model5)

with model5:
    trace5 = pm.sample(tune=2000, target_accept=0.99)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu_pop_mean, mu_pop_variance, x, sigma]

100.00% [12000/12000 02:30<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 161 seconds.

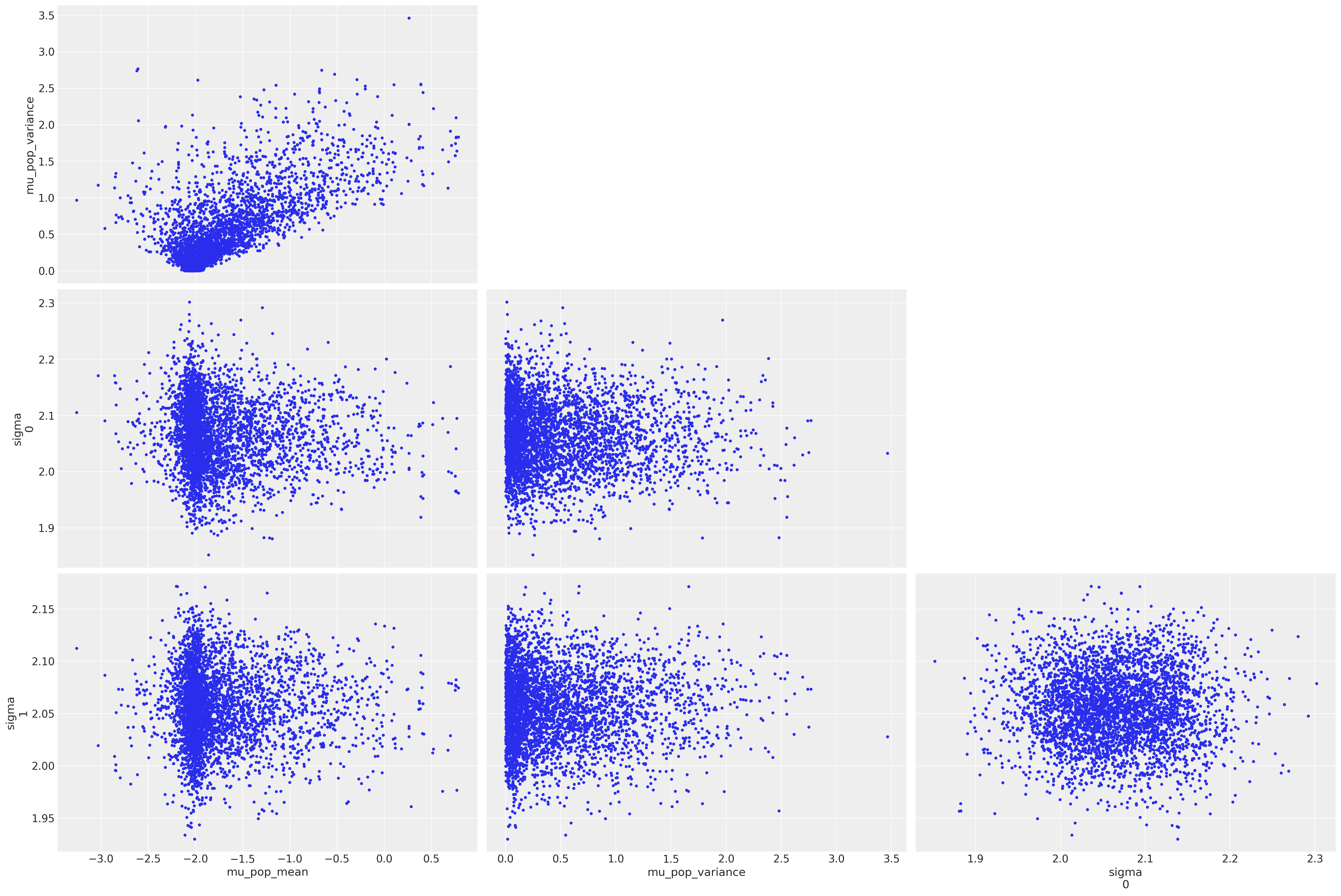
我们可以看到，尽管我们付出了努力，仍然存在一些分歧。绘制样本并突出显示分歧表明（从左上角子图来看）我们的模型存在漏斗问题

az.plot_pair(
    trace5, var_names=["mu_pop_mean", "mu_pop_variance", "sigma"], coords=coords, divergences=True
);

后验预测检查

with model5:
    ppc = pm.sample_posterior_predictive(trace5)

100.00% [4000/4000 00:00<00:00]

fig, ax = plt.subplots(1, 2, figsize=(12, 4), sharey=True)

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
c1.plot(kind="bar", ax=ax[0], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(x="bin1", y="counts1", color="k", alpha=0.2, ax=ax[0])
# Formatting
ax[0].set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax[0].set_title("Six bin discretization of N(-2, 2)")

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
c2.plot(kind="bar", ax=ax[1], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(x="bin2", y="counts2", color="k", alpha=0.2, ax=ax[1])
# Formatting
ax[1].set_xticklabels([f"bin {n}" for n in range(len(c2))])
ax[1].set_title("Seven bin discretization of N(-2, 2)")

Text(0.5, 1.0, 'Seven bin discretization of N(-2, 2)')

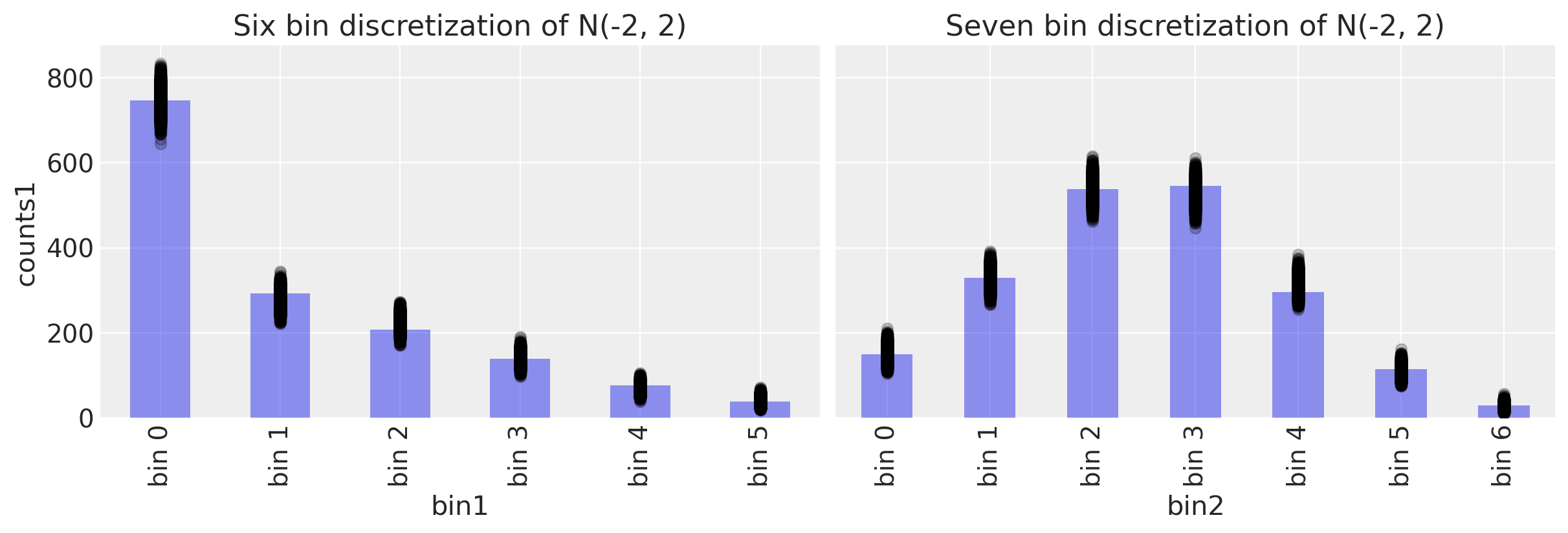
检查后验

研究层面的均值或标准差是否有任何差异的证据？

fig, ax = plt.subplots(1, 2, figsize=(10, 3))

diff = trace5.posterior.mu.sel(study=0) - trace5.posterior.mu.sel(study=1)
az.plot_posterior(diff, ref_val=0, ax=ax[0])
ax[0].set(title="difference in study level mean estimates")

diff = trace5.posterior.sigma.sel(study=0) - trace5.posterior.sigma.sel(study=1)
az.plot_posterior(diff, ref_val=0, ax=ax[1])
ax[1].set(title="difference in study level std estimate");

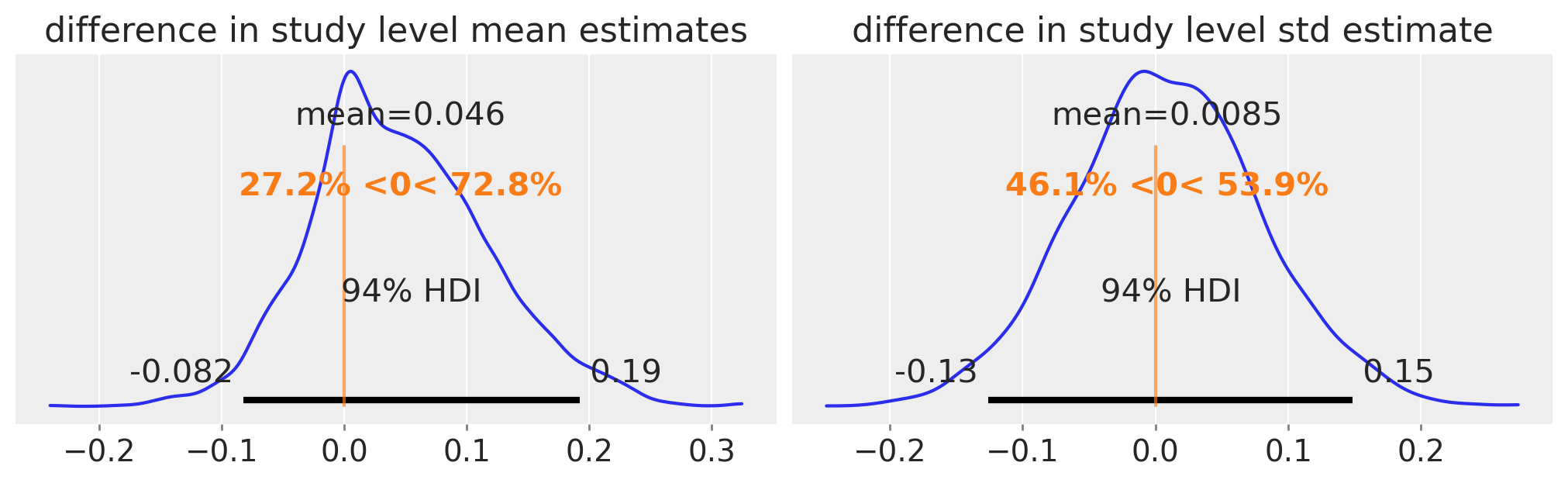
没有令人信服的证据表明总体水平均值和标准差之间存在差异。

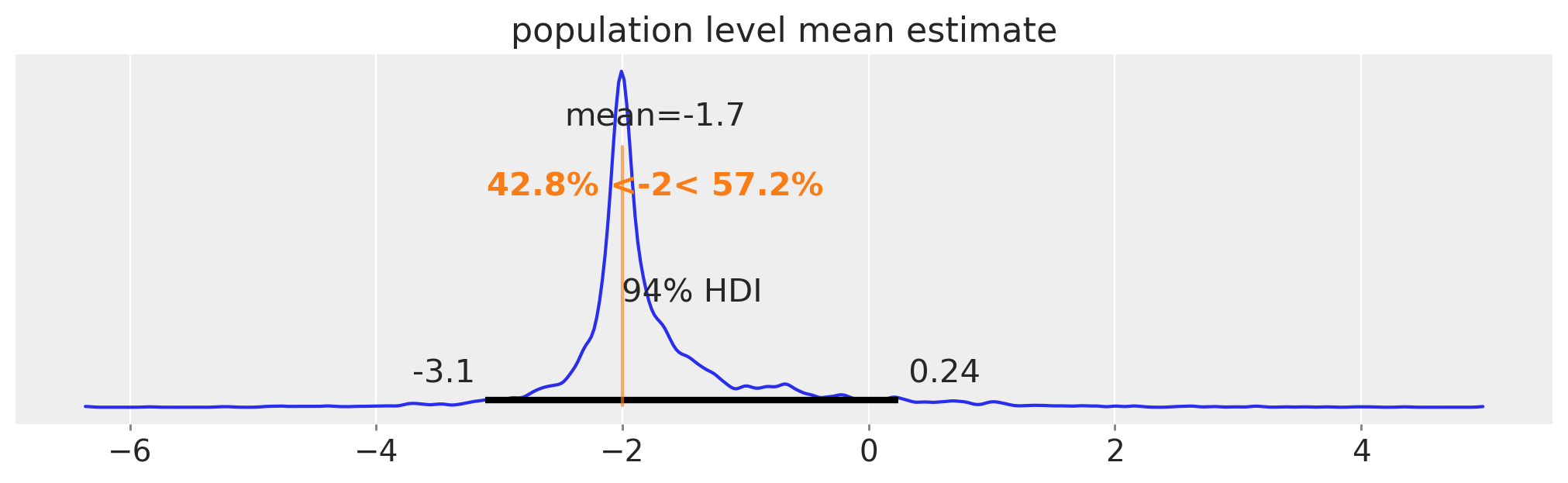
均值参数中的人口水平估计。在这个重新参数化的模型中，没有sigma的人口水平估计。

fig, ax = plt.subplots(figsize=(10, 3))

pop_mean = rng.normal(
    trace5.posterior.mu_pop_mean.values.flatten(), trace5.posterior.mu_pop_variance.values.flatten()
)
az.plot_posterior(pop_mean, ax=ax, ref_val=true_mu)
ax.set(title="population level mean estimate");

另一种可能的解决方案是对组1和组2的研究级别参数进行独立的推断，然后寻找这些参数是否存在差异的证据。采用这种方法效果很好，没有出现分歧，尽管这种方法偏离了我们进行人口级别推断的核心目标。我们没有完全详细地讲解这个例子，而是包含了代码，以防对任何人的用例有所帮助。

with pm.Model(coords=coords) as model5:
    # Study level priors
    mu = pm.Normal("mu", dims='study')
    sigma = pm.HalfNormal("sigma", dims='study')
    
    # Study 1
    probs1 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu[0], sigma=sigma[0]), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs1, np.array([1])]))
    probs1 = pm.Deterministic("normal1_cdf", probs1, dims='bin1')

    # Study 2
    probs2 = pm.math.exp(pm.logcdf(pm.Normal.dist(mu=mu[1], sigma=sigma[1]), d2))
    probs2 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs2, np.array([1])]))
    probs2 = pm.Deterministic("normal2_cdf", probs2, dims='bin2')

    # Likelihood
    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values, dims='bin1')
    pm.Multinomial("counts2", p=probs2, n=c2.sum(), observed=c2.values, dims='bin2')

示例 6：非正态分布

理论上，我们使用的方法是非常通用的。它的依赖关系通常规定得很好：

• 参数分布

• 已知分布支持上的切点，用于对我们的数据进行分箱

• 每个区间的计数（以及因此的比例）

我们现在将通过实证验证，使用相同的方法可以恢复其他分布的参数。我们将从两个假设的（模拟的）研究中近似估计体重指数（BMI）的分布。

在第一个研究中，虚构的研究人员使用了一组阈值，这些阈值为他们提供了许多类别：

• 体重过轻（严重消瘦）：\(< 16\)

• 体重过轻（中度消瘦）：\(16 - 17\)

• 体重过轻（轻度瘦弱）：\(17 - 18.5\)

• 正常范围: \(18.5 - 25\)

• 超重（前肥胖）：\(25 - 30\)

• 肥胖（I级）：\(30 - 35\)

• 肥胖（II级）：\(35 - 40\)

• 肥胖（III级）：\(\ge 40\)

第二组研究人员使用了香港医院管理局推荐的一个分类方案：

• 体重过轻（不健康）：\(< 18.5\)

• 正常范围（健康）：\(18.5 - 23\)

• 超重 I（有风险）：\(23 - 25\)

• 超重 II（中度肥胖）：\(25 - 30\)

• 超重 III（严重肥胖）：\(\ge 30\)

# First discretization
d1 = np.array([16, 17, 18.5, 25, 30, 35, 40])
# Second discretization
d2 = np.array([18.5, 23, 30])

我们假设真实的潜在BMI分布是Gumbel分布，其mu和beta参数分别为20和4。

# True underlying BMI distribution
true_mu, true_beta = 20, 4
BMI = pm.Gumbel.dist(mu=true_mu, beta=true_beta)

# Generate two different sets of random samples from the same Gaussian.
x1 = pm.draw(BMI, 800)
x2 = pm.draw(BMI, 1200)

# Calculate bin counts
c1 = data_to_bincounts(x1, d1)
c2 = data_to_bincounts(x2, d2)

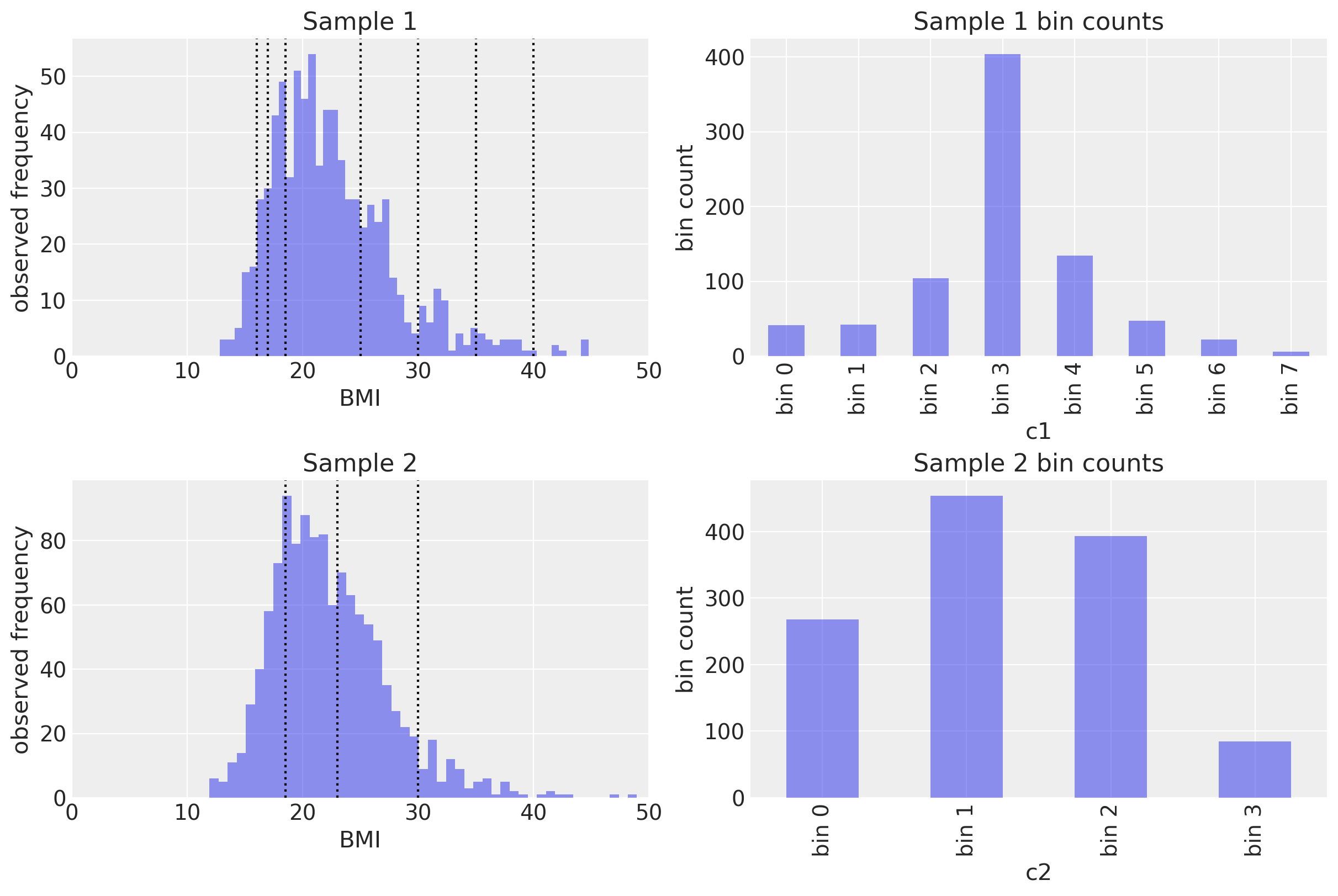
fig, ax = plt.subplots(2, 2, figsize=(12, 8))

# First set of measurements ----------------------------------------------
ax[0, 0].hist(x1, 50, alpha=0.5)

for cut in d1:
    ax[0, 0].axvline(cut, color="k", ls=":")

# Plot observed bin counts
c1.plot(kind="bar", ax=ax[0, 1], alpha=0.5)
ax[0, 1].set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax[0, 1].set(title="Sample 1 bin counts", xlabel="c1", ylabel="bin count")

# Second set of measuremsnts ---------------------------------------------
ax[1, 0].hist(x2, 50, alpha=0.5)

for cut in d2:
    ax[1, 0].axvline(cut, color="k", ls=":")

# Plot observed bin counts
c2.plot(kind="bar", ax=ax[1, 1], alpha=0.5)
ax[1, 1].set_xticklabels([f"bin {n}" for n in range(len(c2))])
ax[1, 1].set(title="Sample 2 bin counts", xlabel="c2", ylabel="bin count")

# format axes ------------------------------------------------------------
ax[0, 0].set(xlim=(0, 50), xlabel="BMI", ylabel="observed frequency", title="Sample 1")
ax[1, 0].set(xlim=(0, 50), xlabel="BMI", ylabel="observed frequency", title="Sample 2");

模型规范

这是上述示例3的一个变体。唯一的更改是：

• 更新概率分布以匹配我们的目标（Gumbel分布）

• 确保我们为目标分布指定了先验，这些先验是基于我们的领域知识而合适的。

with pm.Model() as model6:
    mu = pm.Normal("mu", 20, 5)
    beta = pm.HalfNormal("beta", 10)

    probs1 = pm.math.exp(pm.logcdf(pm.Gumbel.dist(mu=mu, beta=beta), d1))
    probs1 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs1, np.array([1])]))
    probs1 = pm.Deterministic("gumbel_cdf1", probs1)

    probs2 = pm.math.exp(pm.logcdf(pm.Gumbel.dist(mu=mu, beta=beta), d2))
    probs2 = pt.extra_ops.diff(pm.math.concatenate([np.array([0]), probs2, np.array([1])]))
    probs2 = pm.Deterministic("gumbel_cdf2", probs2)

    pm.Multinomial("counts1", p=probs1, n=c1.sum(), observed=c1.values)
    pm.Multinomial("counts2", p=probs2, n=c2.sum(), observed=c2.values)

pm.model_to_graphviz(model6)

with model6:
    trace6 = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, beta]

100.00% [8000/8000 00:02<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 13 seconds.
The acceptance probability does not match the target. It is 0.8809, but should be close to 0.8. Try to increase the number of tuning steps.

后验预测检查

with model6:
    ppc = pm.sample_posterior_predictive(trace6)

100.00% [4000/4000 00:00<00:00]

fig, ax = plt.subplots(1, 2, figsize=(12, 4), sharey=True)

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
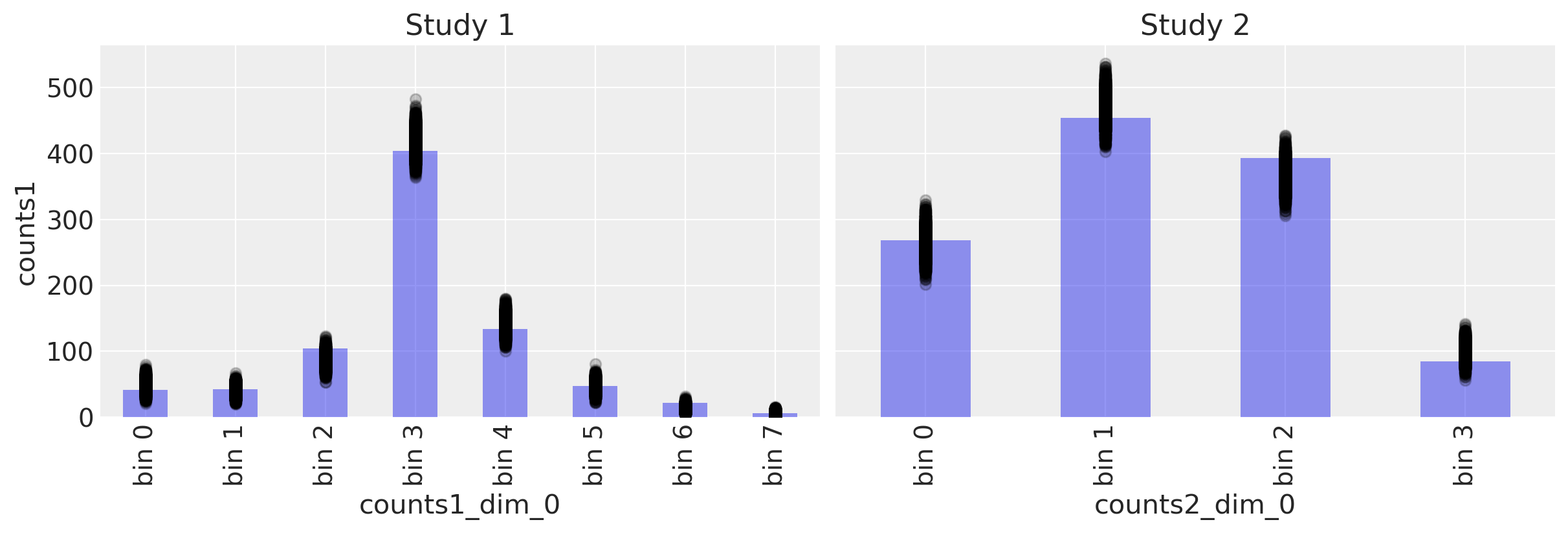
c1.plot(kind="bar", ax=ax[0], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(
    x="counts1_dim_0", y="counts1", color="k", alpha=0.2, ax=ax[0]
)
# Formatting
ax[0].set_xticklabels([f"bin {n}" for n in range(len(c1))])
ax[0].set_title("Study 1")

# Study 1 ----------------------------------------------------------------
# Plot observed bin counts
c2.plot(kind="bar", ax=ax[1], alpha=0.5)
# Plot posterior predictive
ppc.posterior_predictive.plot.scatter(
    x="counts2_dim_0", y="counts2", color="k", alpha=0.2, ax=ax[1]
)
# Formatting
ax[1].set_xticklabels([f"bin {n}" for n in range(len(c2))])
ax[1].set_title("Study 2")

Text(0.5, 1.0, 'Study 2')

恢复参数

az.plot_posterior(trace6, var_names=["mu", "beta"], ref_val=[true_mu, true_beta]);

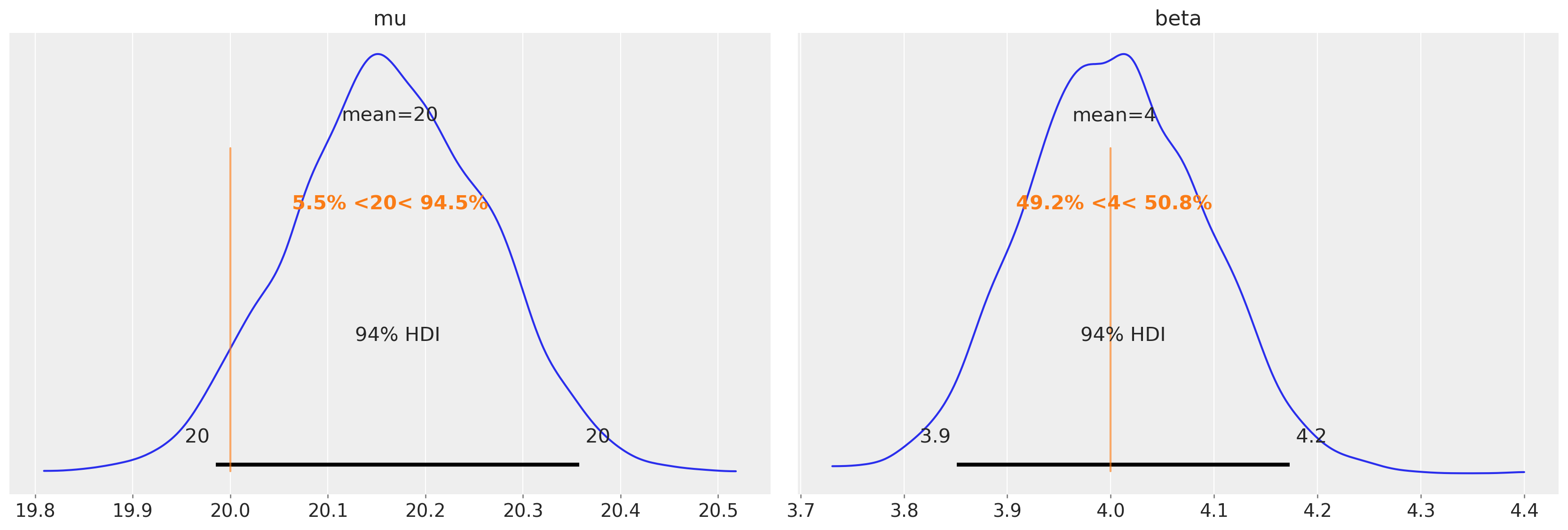
我们可以看到，我们成功地恢复了已知的基础BMI人群参数。

如果我们对测试研究1和研究2中的BMI分布是否存在差异感兴趣，那么我们可以简单地采用示例6中的模型，并将其调整为与我们所需的目标分布一起操作，就像我们在本示例中所做的那样。

结论

如您所见，这种用于估计高斯和非高斯分布的已知参数的方法效果非常好。 虽然这些示例已应用于合成数据，但进行此类参数恢复研究至关重要。如果我们尝试从计数中恢复总体水平参数，并且在知道真实情况时无法做到这一点，那么这将表明该方法不可信。但各种参数恢复示例表明，我们实际上可以从分箱和不同分箱的数据中准确恢复总体水平参数。

这里需要注意的一个关键技术点是，当我们传入观测计数时，它们应该严格按照CDF顺序排列。 这里没有展示的是我们打乱计数顺序的实验； 在那里，对潜在分布参数的估计是不正确的。

我们在这里展示了一系列不同的示例，这些示例清楚地表明，一般方法可以很容易地适应所面临的特定情况或研究问题。这些方法应该很容易适应新颖但相关的数据科学情况。

作者

• 由 Eric Ma 和 Benjamin T. Vincent 于2021年9月撰写（pymc-examples#229）

• 由 Fernando Irarrazaval 于 2022 年 6 月更新以在 PyMC v4 中运行（pymc-examples#366）

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p aeppl,xarray

Last updated: Sat Jun 04 2022

Python implementation: CPython
Python version       : 3.10.4
IPython version      : 8.3.0

aeppl : 0.0.27
xarray: 2022.3.0

pandas    : 1.4.2
seaborn   : 0.11.2
matplotlib: 3.5.1
pymc      : 4.0.0b6
arviz     : 0.12.1
numpy     : 1.22.4
pytensor    : 2.5.1

Watermark: 2.3.1