双重差分法#

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

介绍#

本笔记本简要概述了差异中的差异方法在因果推断中的应用，并展示了一个在贝叶斯框架下使用PyMC进行此类分析的工作示例。虽然本笔记本提供了该方法的高层次概述，但我建议参考两本关于因果推断的优秀教科书。《The Effect》和《Causal Inference: The Mixtape》都有专门介绍差异中的差异的章节。

双重差分法是一种适用于因果推断的好方法，如果：

你想知道治疗/干预的因果影响
您有预处理和后处理措施
你既有处理组也有对照组
治疗并非通过随机分配进行，也就是说，你处于一个准实验环境中。

否则，可能有更适合的方法可以使用。

需要注意的是，我们希望估计治疗的因果影响涉及反事实思维。这是因为我们在问“如果未进行治疗，治疗组的治疗后结果会是什么？”但我们永远无法观察到这一点。

示例#

一个经典的例子是由Card和克鲁格[1993]进行的研究。该研究考察了提高最低工资对快餐业就业的影响。这是一个准实验设置，因为干预（最低工资的增加）不是随机应用于不同的地理单位（例如州）。干预于1992年4月在新泽西州实施。如果他们仅在新泽西州测量干预前后的就业率，那么他们将无法控制随时间变化的遗漏变量（例如季节性影响），这些变量可能为就业率的变化提供替代的因果解释。但通过选择一个控制州（宾夕法尼亚州），这使得人们可以推断宾夕法尼亚州的就业变化将匹配反事实——如果新泽西州没有接受干预，会发生什么？

因果DAG#

差分中的差分的因果DAG如下所示。它表示：

观察对象的处理状态受到组别和时间的影响。请注意，处理和组别是不同的概念。组别可以是实验组或对照组，但实验组只有在干预时间之后才会被“处理”，因此处理状态取决于组别和时间。
测量的结果受到时间、组别和治疗的因果影响。
不考虑额外的因果影响。

我们主要关注治疗对结果的影响以及这种影响如何随时间变化（从治疗前到治疗后）。如果我们只关注治疗组的治疗、时间和结果（即没有对照组），那么我们将无法将结果的变化归因于治疗，而不是治疗组在时间推移中受到的其他多种因素。换句话说，治疗将完全由时间决定，因此无法区分前后结果的变化是由治疗还是时间引起的。

但通过添加一个对照组，我们能够比较对照组随时间的变化和处理组随时间的变化。差异中的差异方法中的一个关键假设是平行趋势假设——即两组在时间上以相似的方式变化。换句话说，如果对照组和处理组在时间上以相似的方式变化，那么我们可以相当确信，组间随时间的差异是由于处理引起的。

定义差异中的差异模型#

注意：我定义这个模型的方式与你在其他来源中可能找到的略有不同。这是为了便于在本笔记本后面的部分进行反事实推理，并强调关于连续时间趋势的假设。

首先，让我们定义一个Python函数来计算结果的期望值：

def outcome(t, control_intercept, treat_intercept_delta, trend, Δ, group, treated):
    return control_intercept + (treat_intercept_delta * group) + (t * trend) + (Δ * treated * group)

但我们应该用数学符号更仔细地审视这一点。第 \(i^{th}\) 个观测值的期望值是 \(\mu_i\)，其定义为：

\[ \mu_i = \beta_{c} + (\beta_{\Delta} \cdot \mathrm{group}_i) + (\mathrm{trend} \cdot t_i) + (\Delta \cdot \mathrm{treated}_i \cdot \mathrm{group}_i) \]

其中包含以下参数：

\(\beta_c\) 是控制组的截距
\(\beta_{\Delta}\) 是处理组截距相对于对照组截距的偏差
\(\Delta\) 是治疗的因果影响
\(\mathrm{trend}\) 是斜率，模型的核心假设是两个组的斜率相同

以及以下观测数据：

\(t_i\) 是时间，方便地缩放，使得干预前的测量时间在 \(t=0\)，干预后的测量时间在 \(t=1\)
\(\mathrm{group}_i\) 是一个用于控制组（\(g=0\)）或处理组（\(g=1\)）的虚拟变量
\(\mathrm{treated}_i\) 是一个用于表示未处理或已处理的二元指示变量。这是时间和组的函数：\(\mathrm{treated}_i = f(t_i, \mathrm{group}_i)\)。

我们可以通过查看上面的DAG并通过编写一个Python函数来定义这个函数，来强调这一点，即治疗受到时间和组的因果影响。

def is_treated(t, intervention_time, group):
    return (t > intervention_time) * group

可视化差异中的差异模型#

很多时候，一幅图胜过千言万语，所以如果上面的描述令人困惑，那么我建议在从下面的图中获得更多直观感受后再重新阅读。

# true parameters
control_intercept = 1
treat_intercept_delta = 0.25
trend = 1
Δ = 0.5
intervention_time = 0.5

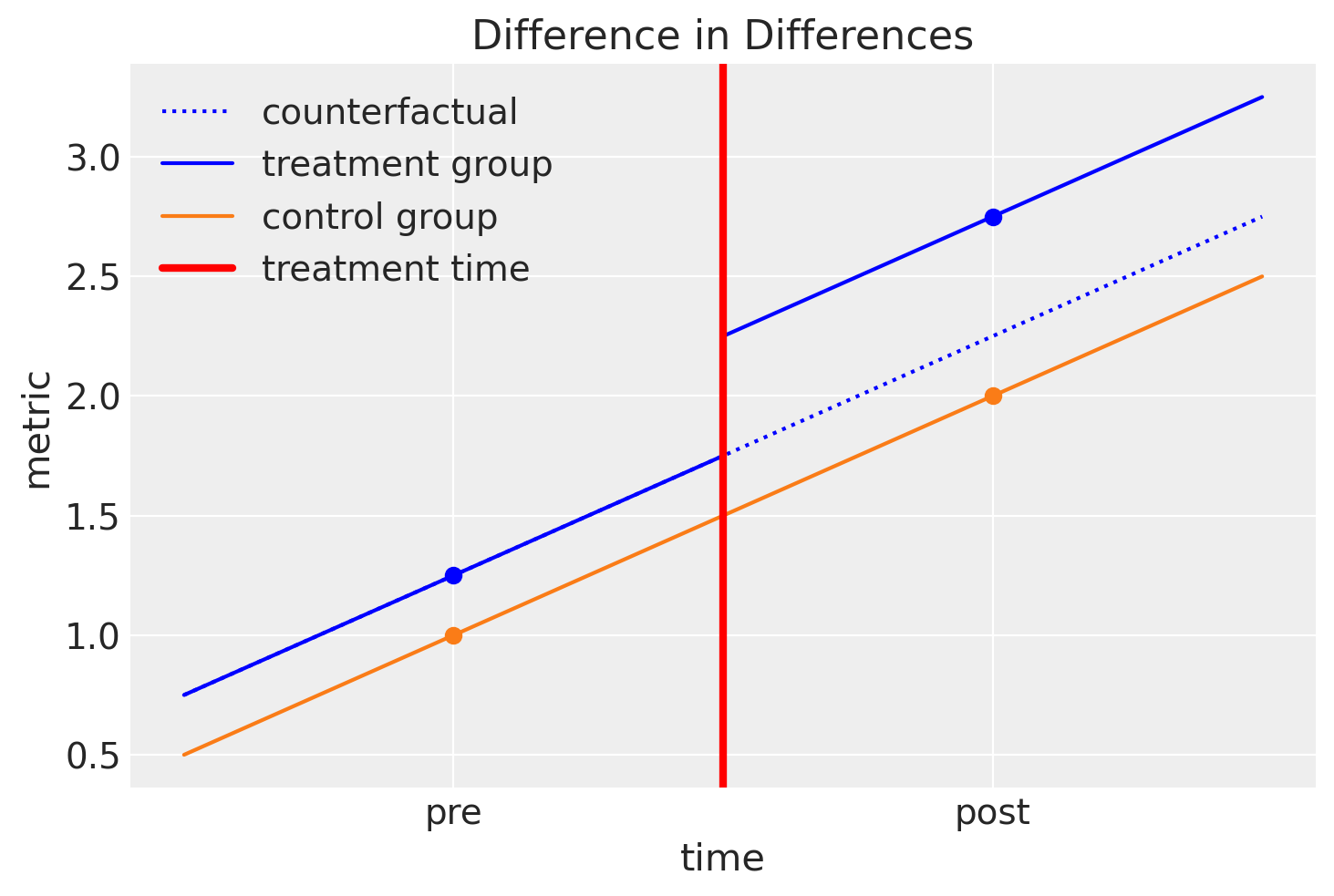
../../../_images/8f0282bc3fafdc3f95d353ed712496d5fab4d0c009f5c0d8ecaf42f7a8626b37.png

因此，我们可以通过查看这张图来总结差异分析的直觉：

我们假设处理组和对照组随着时间的推移以相似的方式演变。
我们可以轻松估计对照组从治疗前到治疗后的斜率。
我们可以进行反事实思考，并可以问：“如果治疗组没有接受治疗，他们的治疗后结果会是什么？”

如果我们能够回答这个问题并估计这个反事实的数量，那么我们可以问：“治疗的因果影响是什么？” 我们可以通过比较治疗组在治疗后的观察结果与反事实数量来回答这个问题。

我们可以从视觉上思考这个问题，并以另一种方式陈述……通过观察对照组的前后差异，我们可以将对照组和处理组前后差异的任何差异归因于处理的治疗效果。这就是为什么这种方法被称为双重差分法。

生成一个合成数据集#

df = pd.DataFrame(
    {
        "group": [0, 0, 1, 1] * 10,
        "t": [0.0, 1.0, 0.0, 1.0] * 10,
        "unit": np.concatenate([[i] * 2 for i in range(20)]),
    }
)

df["treated"] = is_treated(df["t"], intervention_time, df["group"])

df["y"] = outcome(
    df["t"],
    control_intercept,
    treat_intercept_delta,
    trend,
    Δ,
    df["group"],
    df["treated"],
)
df["y"] += rng.normal(0, 0.1, df.shape[0])
df.head()

	group	t	unit	treated	y
0	0	0.0	0	0	0.977736
1	0	1.0	0	0	2.132566
2	1	0.0	1	0	1.192903
3	1	1.0	1	1	2.816825
4	0	0.0	2	0	1.114538

因此我们看到我们拥有仅在两个时间点上的面板数据：干预前（\(t=0\)）和干预后（\(t=1\)）的测量时间。

sns.lineplot(df, x="t", y="y", hue="group", units="unit", estimator=None)
sns.scatterplot(df, x="t", y="y", hue="group");

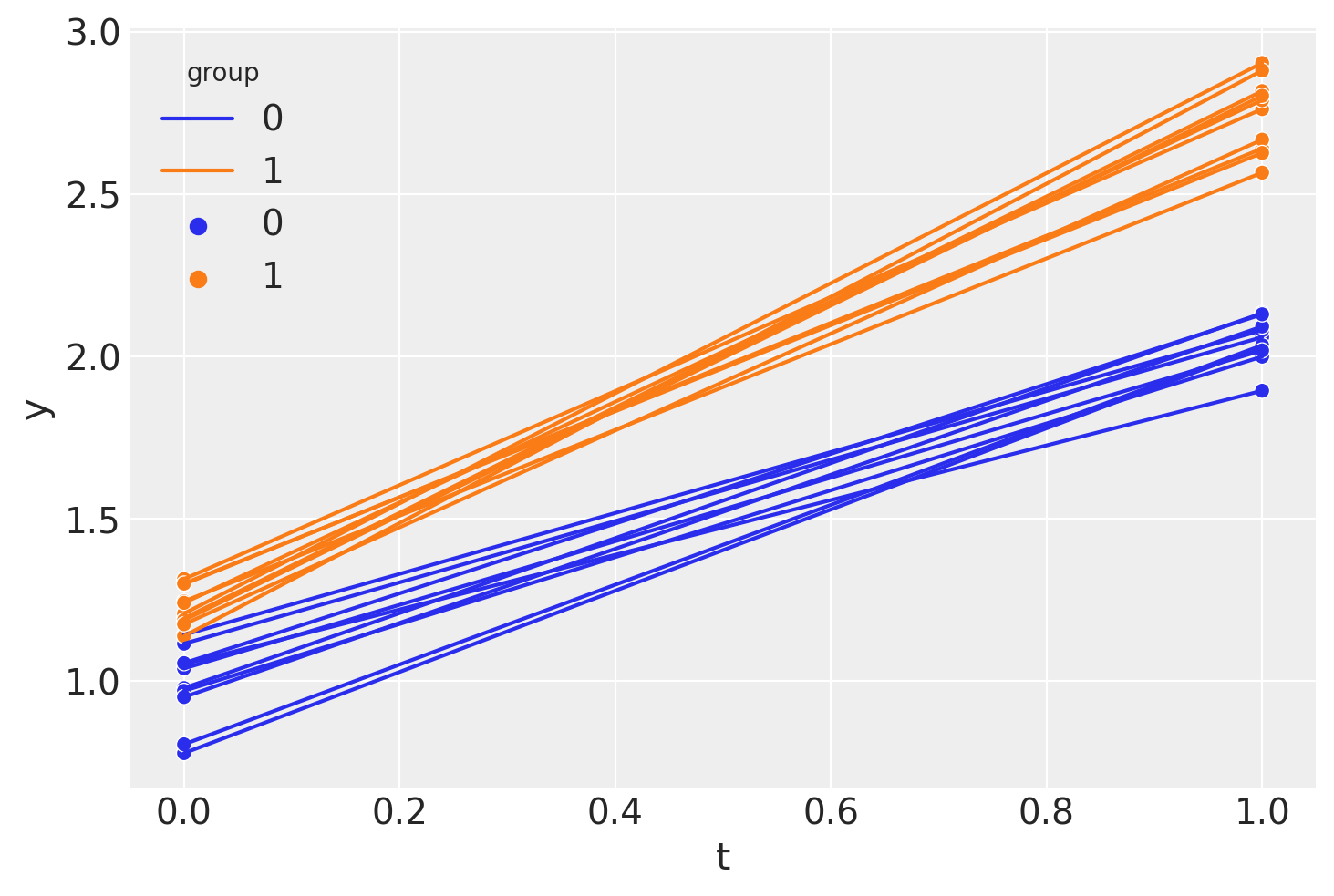
../../../_images/aac2ccaccb8afd9cb8fd093d8f38a67ec1e1fc90635e044639451b4cbf59366a.png

如果我们愿意，我们可以像这样计算差异差异的点估计（在非回归方法中）。

diff_control = (
    df.loc[(df["t"] == 1) & (df["group"] == 0)]["y"].mean()
    - df.loc[(df["t"] == 0) & (df["group"] == 0)]["y"].mean()
)
print(f"Pre/post difference in control group = {diff_control:.2f}")

diff_treat = (
    df.loc[(df["t"] == 1) & (df["group"] == 1)]["y"].mean()
    - df.loc[(df["t"] == 0) & (df["group"] == 1)]["y"].mean()
)

print(f"Pre/post difference in treatment group = {diff_treat:.2f}")

diff_in_diff = diff_treat - diff_control
print(f"Difference in differences = {diff_in_diff:.2f}")

Pre/post difference in control group = 1.06
Pre/post difference in treatment group = 1.52
Difference in differences = 0.46

但是等等，我们是贝叶斯主义者！让我们用贝叶斯方法…

贝叶斯差异中的差异#

PyMC 模型#

对于那些已经精通PyMC的人来说，你可以看到这个模型非常简单。我们只有几个组件：

定义数据节点。这是可选的，但在我们进行后验预测检查和反事实推断时会很有用
定义先验
使用我们已经在上面定义的 outcome 函数来评估模型期望
定义一个正态似然分布。

with pm.Model() as model:
    # data
    t = pm.MutableData("t", df["t"].values, dims="obs_idx")
    treated = pm.MutableData("treated", df["treated"].values, dims="obs_idx")
    group = pm.MutableData("group", df["group"].values, dims="obs_idx")
    # priors
    _control_intercept = pm.Normal("control_intercept", 0, 5)
    _treat_intercept_delta = pm.Normal("treat_intercept_delta", 0, 1)
    _trend = pm.Normal("trend", 0, 5)
    _Δ = pm.Normal("Δ", 0, 1)
    sigma = pm.HalfNormal("sigma", 1)
    # expectation
    mu = pm.Deterministic(
        "mu",
        outcome(t, _control_intercept, _treat_intercept_delta, _trend, _Δ, group, treated),
        dims="obs_idx",
    )
    # likelihood
    pm.Normal("obs", mu, sigma, observed=df["y"].values, dims="obs_idx")

pm.model_to_graphviz(model)

../../../_images/6be698a56d1eec8ba4cbd0eef5c316721dcf486fb3740423701846a374388b17.svg

推理#

with model:
    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [control_intercept, treat_intercept_delta, trend, Δ, sigma]

100.00% [8000/8000 00:01<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.

az.plot_trace(idata, var_names="~mu");

../../../_images/0aa4f8512300536980322a1e0ffebea78965eaf4b2b354b9e3a3aa0e0604cf6d.png

后验预测#

注意：从技术上讲，我们正在对 \(\mu\) 进行“前推预测”，因为这是一个确定性的输入函数。如果我们生成预测的观测值，后验预测将是一个更合适的标签——这些观测值将基于我们为数据指定的正态似然性而具有随机性。尽管如此，本节仍称为“后验预测”，以强调我们遵循贝叶斯工作流程的事实。

# pushforward predictions for control group
with model:
    group_control = [0] * len(ti)  # must be integers
    treated = [0] * len(ti)  # must be integers
    pm.set_data({"t": ti, "group": group_control, "treated": treated})
    ppc_control = pm.sample_posterior_predictive(idata, var_names=["mu"])

# pushforward predictions for treatment group
with model:
    group = [1] * len(ti)  # must be integers
    pm.set_data(
        {
            "t": ti,
            "group": group,
            "treated": is_treated(ti, intervention_time, group),
        }
    )
    ppc_treatment = pm.sample_posterior_predictive(idata, var_names=["mu"])

# counterfactual: what do we predict of the treatment group (after the intervention) if
# they had _not_ been treated?
t_counterfactual = np.linspace(intervention_time, 1.5, 100)
with model:
    group = [1] * len(t_counterfactual)  # must be integers
    pm.set_data(
        {
            "t": t_counterfactual,
            "group": group,
            "treated": [0] * len(t_counterfactual),  # THIS IS OUR COUNTERFACTUAL
        }
    )
    ppc_counterfactual = pm.sample_posterior_predictive(idata, var_names=["mu"])

Sampling: []

100.00% [4000/4000 00:00<00:00]

Sampling: []

100.00% [4000/4000 00:00<00:00]

Sampling: []

100.00% [4000/4000 00:00<00:00]

总结#

我们可以绘制我们学到的内容如下：

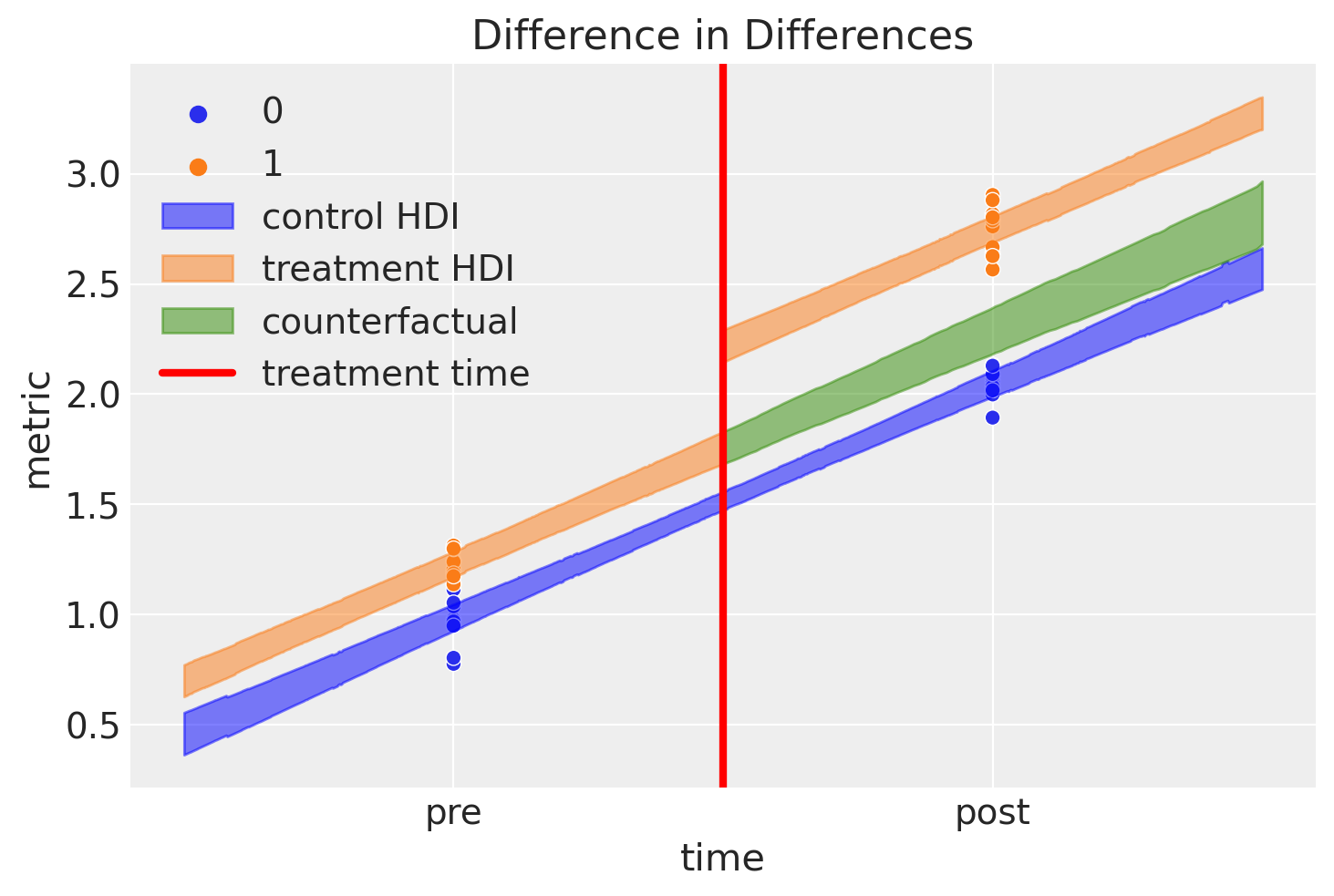
../../../_images/f73f8c06a0acda00bb74905c6054e1b9f5b99b181a97fde2803d29f810f6fc16.png

这是一个很棒的图表，但这里有很多内容，所以我们来逐一看看：

蓝色阴影区域表示对照组期望值的可信区域
橙色阴影区域表示治疗组的相似区域。我们可以看到结果在干预后立即跳跃。
绿色阴影区域是非常新颖且不错的。这代表了我们对于如果治疗组从未接受治疗的反事实推断。根据定义，我们从未对干预时间后未接受治疗的治疗组项目进行过任何观察。然而，通过笔记本顶部描述的模型和概述的贝叶斯推断方法，我们可以对这些假设问题进行推理。
这个反事实期望与观察到的值（治疗条件下的治疗后）之间的差异代表了我们对治疗因果影响的推断。让我们更详细地看一下这个后验分布：

ax = az.plot_posterior(idata.posterior["Δ"], ref_val=Δ, figsize=(10, 3))
ax.set(title=r"Posterior distribution of causal impact of treatment, $\Delta$");

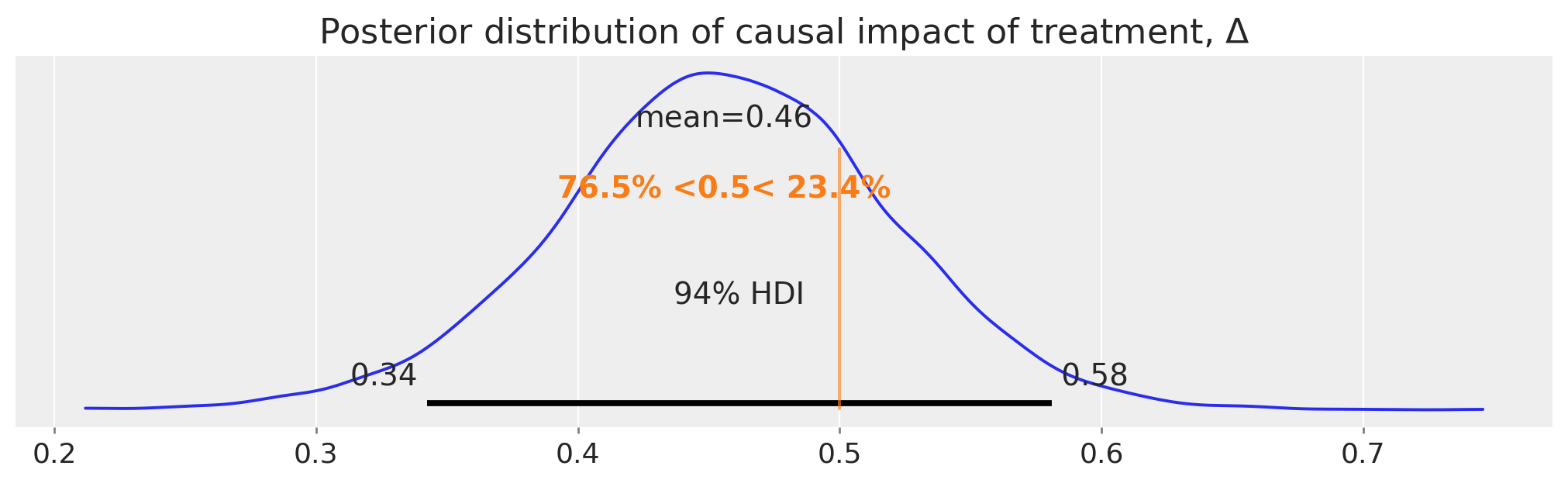
../../../_images/2445f6b46608b7733d8de7650815033101f9fc0268fd7ab61ecd052dfcb41352.png

所以，我们得到了完整的后验分布，使用差异中的差异方法估计了我们的因果影响。

概述#

当然，在使用双重差分法进行实际应用时，还需要更多的尽职调查。读者可以参考引言中列出的教科书以及一篇有用的综述论文[Wing 等，2018]，该论文更详细地涵盖了重要的背景问题。此外，Bertrand 等 [2004]对该方法持怀疑态度，并提出了他们所强调的一些问题的解决方案。

参考资料#

[1]

尼克·亨廷顿-克莱因。效果：研究设计和因果关系导论。查普曼和霍尔/CRC，2021年。

[2]

斯科特·坎宁安。因果推断：混音带。耶鲁大学出版社，2021年。

[3]

大卫·卡德和艾伦·B·克鲁格。最低工资与就业：新泽西和宾夕法尼亚州快餐业案例研究。1993年。

[4]

科迪·温、科萨利·西蒙和里卡多·A·贝洛-戈麦斯。设计差异中的差异研究：公共卫生政策研究的最佳实践。《公共卫生年鉴》，39(1):453–469, 2018。

[5]

玛丽安·伯特兰，埃丝特·迪弗洛，和森德希尔·穆拉伊纳丹。我们应该对差异中的差异估计有多少信任？经济学季刊，119(1):249–275, 2004.

作者#

由 Benjamin T. Vincent 于2022年9月撰写（#424）。
由Benjamin T. Vincent于2023年2月更新，以在PyMC v5上运行

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Wed Feb 01 2023

Python implementation: CPython
Python version       : 3.11.0
IPython version      : 8.9.0

pytensor: 2.8.11
aeppl   : not installed
xarray  : 2023.1.0

arviz     : 0.14.0
pymc      : 5.0.1
pandas    : 1.5.3
matplotlib: 3.6.3
numpy     : 1.24.1
seaborn   : 0.12.2

Watermark: 2.3.1

分类

标签

双重差分法#

介绍#

示例#

因果DAG#

定义差异中的差异模型#

可视化差异中的差异模型#

生成一个合成数据集#

贝叶斯差异中的差异#

PyMC 模型#

推理#

后验预测#

总结#

概述#

参考资料#

作者#

水印#