高斯过程:潜在变量实现#
The gp.Latent 类是高斯过程的直接实现,没有近似。给定均值和协方差函数,我们可以在函数 \(f(x)\) 上放置一个先验,
它被称为“Latent”,因为GP本身作为潜在变量包含在模型中,它不像gp.Marginal那样被边缘化。与gp.Latent不同,在使用gp.Marginal时,你不会在trace中找到GP后验的样本。这是GP的最直接实现,因为它不假设特定的似然函数或数据或协方差矩阵中的特定结构。
The .prior 方法#
The prior 方法在 PyMC 模型中为 GP 函数值的向量 \(\mathbf{f}\) 添加了一个多元正态先验分布。
其中向量 \(\mathbf{m}_x\) 和矩阵 \(\mathbf{K}_{xx}\) 是在输入 \(x\) 上评估的均值向量和协方差矩阵。默认情况下,PyMC 在后台通过使用其协方差矩阵的 Cholesky 因子旋转来重新参数化 f 的先验。这通过减少变换后的随机变量 v 的后验中的协方差来改善采样。重新参数化的模型是,
有关此重新参数化的更多信息,请参阅关于从多元分布中抽取值的部分。
The .conditional 方法#
条件方法实现了原始数据集中不存在的函数值的预测分布。这个分布是,
使用上面定义的相同的 gp 对象,我们可以通过以下方式构建一个具有此分布的随机变量:
# vector of new X points we want to predict the function at
X_star = np.linspace(0, 2, 100)[:, None]
with latent_gp_model:
f_star = gp.conditional("f_star", X_star)
示例 1:带有学生-T 分布噪声的回归#
以下是一个示例,展示了如何使用 gp.Latent 类指定一个带有 GP 先验的简单模型。我们使用 GP 生成数据,以便验证我们执行的推理是否正确。请注意,似然函数不是正态分布,而是独立同分布的学生-T 分布。对于似然函数为高斯分布时更高效的实现,请使用 gp.Marginal。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8998
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
n = 50 # The number of data points
X = np.linspace(0, 10, n)[:, None] # The inputs to the GP must be arranged as a column vector
# Define the true covariance function and its parameters
ell_true = 1.0
eta_true = 4.0
cov_func = eta_true**2 * pm.gp.cov.ExpQuad(1, ell_true)
# A mean function that is zero everywhere
mean_func = pm.gp.mean.Zero()
# The latent function values are one sample from a multivariate normal
f_true = pm.draw(pm.MvNormal.dist(mu=mean_func(X), cov=cov_func(X)), 1, random_seed=rng)
# The observed data is the latent function plus a small amount of T distributed noise
# The standard deviation of the noise is `sigma`, and the degrees of freedom is `nu`
sigma_true = 1.0
nu_true = 5.0
y = f_true + sigma_true * rng.standard_t(df=nu_true, size=n)
## Plot the data and the unobserved latent function
fig = plt.figure(figsize=(10, 4))
ax = fig.gca()
ax.plot(X, f_true, "dodgerblue", lw=3, label="True generating function 'f'")
ax.plot(X, y, "ok", ms=3, label="Observed data")
ax.set_xlabel("X")
ax.set_ylabel("y")
plt.legend(frameon=True);
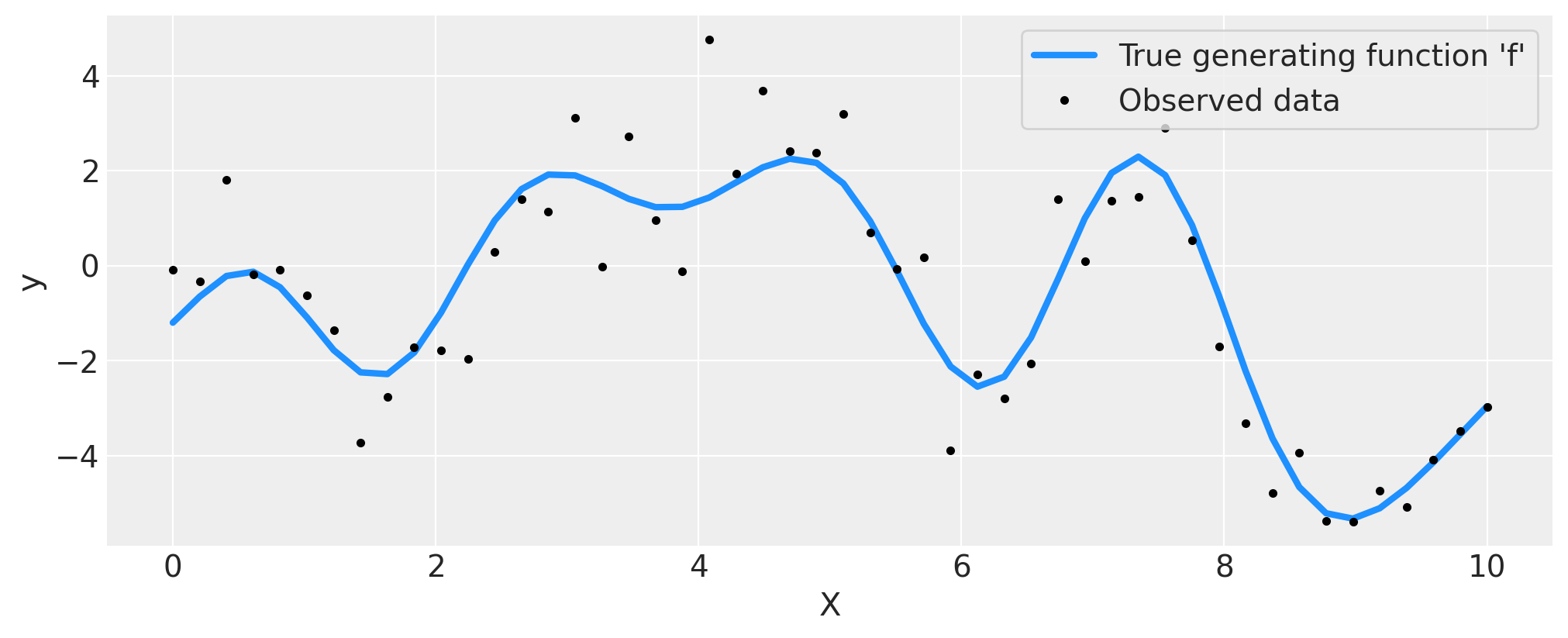
上述数据展示了未知函数 \(f(x)\) 的观测值,用黑色圆点标记,这些观测值受到了噪声的干扰。真实函数以蓝色显示。
在 PyMC 中编写模型代码#
这是在PyMC中的模型。我们使用了一个信息丰富的pm.Gamma(alpha=2, beta=1)先验分布在长度尺度参数上,并且对协方差函数尺度以及噪声尺度使用了弱信息性的pm.HalfNormal(sigma=5)先验分布。噪声的自由度参数被赋予了一个pm.Gamma(2, 0.5)先验分布。最后,在未知函数上放置了一个GP先验。有关在高斯过程模型中选择先验的更多信息,请查看Stan团队的建议。
with pm.Model() as model:
ell = pm.Gamma("ell", alpha=2, beta=1)
eta = pm.HalfNormal("eta", sigma=5)
cov = eta**2 * pm.gp.cov.ExpQuad(1, ell)
gp = pm.gp.Latent(cov_func=cov)
f = gp.prior("f", X=X)
sigma = pm.HalfNormal("sigma", sigma=2.0)
nu = 1 + pm.Gamma(
"nu", alpha=2, beta=0.1
) # add one because student t is undefined for degrees of freedom less than one
y_ = pm.StudentT("y", mu=f, lam=1.0 / sigma, nu=nu, observed=y)
idata = pm.sample(nuts_sampler="numpyro")
# check Rhat, values above 1 may indicate convergence issues
n_nonconverged = int(
np.sum(az.rhat(idata)[["eta", "ell", "sigma", "f_rotated_"]].to_array() > 1.03).values
)
if n_nonconverged == 0:
print("No Rhat values above 1.03, \N{check mark}")
else:
print(f"The MCMC chains for {n_nonconverged} RVs appear not to have converged.")
No Rhat values above 1.03, ✓
结果#
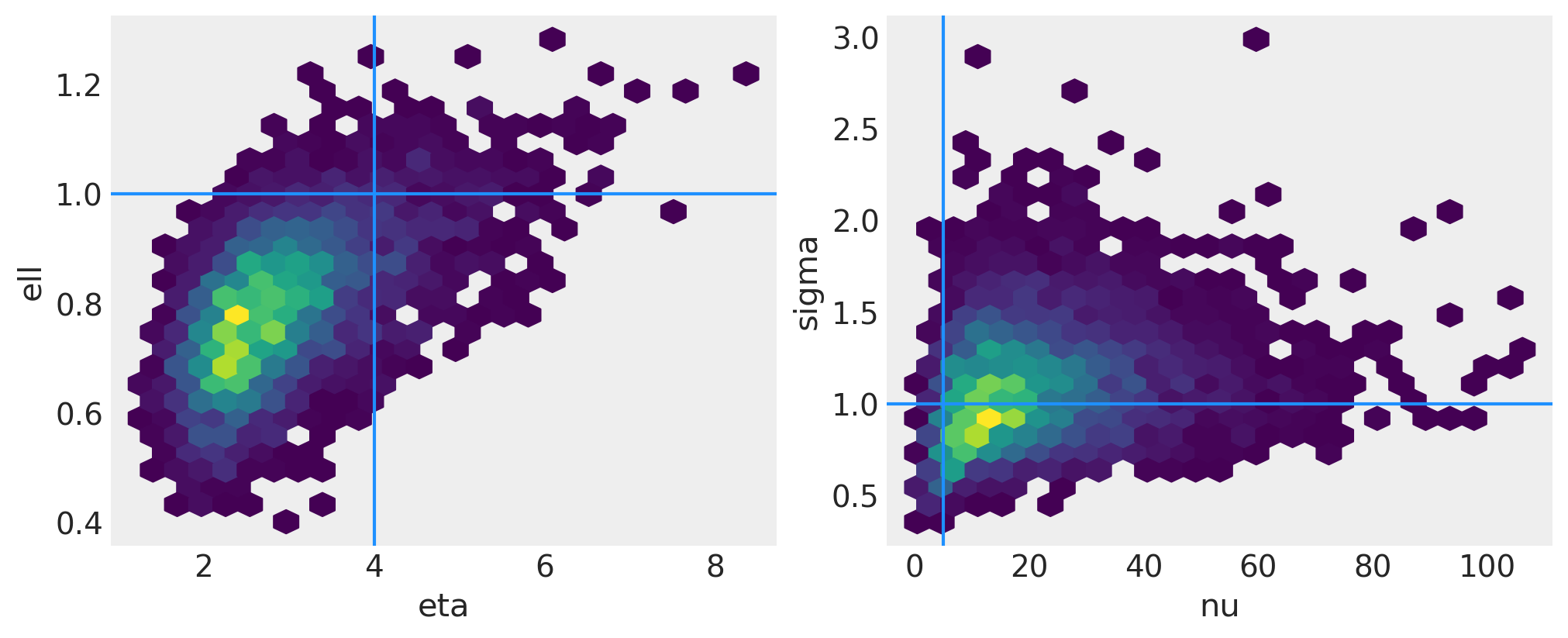
两个协方差函数超参数的联合后验在下图的左侧面板中绘制。在右侧面板中是噪声标准差和似然度自由度参数的联合后验。浅蓝色线显示了用于从GP中绘制函数的真实值。
fig, axs = plt.subplots(1, 2, figsize=(10, 4))
axs = axs.flatten()
# plot eta vs ell
az.plot_pair(
idata,
var_names=["eta", "ell"],
kind=["hexbin"],
ax=axs[0],
gridsize=25,
divergences=True,
)
axs[0].axvline(x=eta_true, color="dodgerblue")
axs[0].axhline(y=ell_true, color="dodgerblue")
# plot nu vs sigma
az.plot_pair(
idata,
var_names=["nu", "sigma"],
kind=["hexbin"],
ax=axs[1],
gridsize=25,
divergences=True,
)
axs[1].axvline(x=nu_true, color="dodgerblue")
axs[1].axhline(y=sigma_true, color="dodgerblue");
f_post = az.extract(idata, var_names="f").transpose("sample", ...)
f_post
<xarray.DataArray 'f' (sample: 4000, f_dim_0: 50)> Size: 2MB
array([[-0.02178219, 0.48692574, 0.72459977, ..., -3.95601759,
-2.98300033, -1.73010505],
[-0.09583607, 0.51662223, 0.77188372, ..., -3.83529288,
-3.59571791, -3.08346489],
[ 0.28659004, 0.22130982, 0.47902239, ..., -3.7474786 ,
-3.42978883, -3.63249247],
...,
[-0.34645708, 0.32101281, 0.54055127, ..., -5.29751615,
-4.60317113, -3.6833632 ],
[-0.43322884, 0.25015173, 0.77657642, ..., -3.90482847,
-3.7119477 , -3.38187578],
[-1.0782359 , -0.83568734, -0.65140178, ..., -4.15961319,
-3.89080578, -3.5752233 ]])
Coordinates:
* f_dim_0 (f_dim_0) int64 400B 0 1 2 3 4 5 6 7 8 ... 42 43 44 45 46 47 48 49
* sample (sample) object 32kB MultiIndex
* chain (sample) int64 32kB 0 0 0 0 0 0 0 0 0 0 0 ... 3 3 3 3 3 3 3 3 3 3 3
* draw (sample) int64 32kB 0 1 2 3 4 5 6 7 ... 993 994 995 996 997 998 999下面是GP的后验概率,
# plot the results
fig = plt.figure(figsize=(10, 4))
ax = fig.gca()
# plot the samples from the gp posterior with samples and shading
from pymc.gp.util import plot_gp_dist
f_post = az.extract(idata, var_names="f").transpose("sample", ...)
plot_gp_dist(ax, f_post, X)
# plot the data and the true latent function
ax.plot(X, f_true, "dodgerblue", lw=3, label="True generating function 'f'")
ax.plot(X, y, "ok", ms=3, label="Observed data")
# axis labels and title
plt.xlabel("X")
plt.ylabel("True f(x)")
plt.title("Posterior distribution over $f(x)$ at the observed values")
plt.legend();
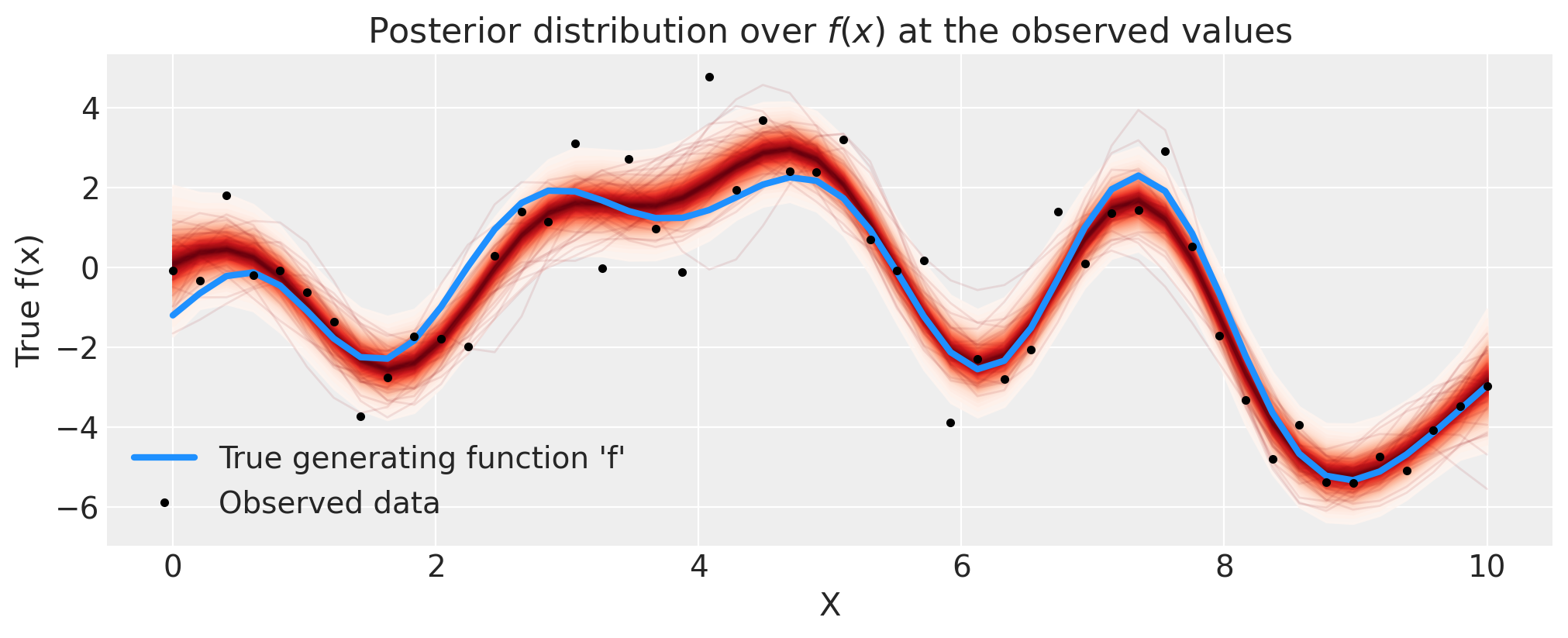
正如红色阴影所示,GP先验在函数上的后验很好地表示了拟合以及由加性噪声引起的不确定性。由于学生-T噪声模型的离群值,结果也没有过拟合。
使用.conditional进行预测#
接下来,我们通过添加条件分布来扩展模型,以便我们可以在新的 \(x\) 位置进行预测。让我们看看外推到更高 \(x\) 的情况。为此,我们通过 conditional 分布扩展我们的 model。然后,我们可以使用 trace 和 sample_posterior_predictive 函数从中进行采样。
这与Stan使用其generated quantities {...}块的方式类似。我们本可以在进行NUTS采样之前将gp.conditional包含在模型中,但将这些步骤分开更为高效。
n_new = 200
X_new = np.linspace(-4, 14, n_new)[:, None]
with model:
# add the GP conditional to the model, given the new X values
f_pred = gp.conditional("f_pred", X_new, jitter=1e-4)
# Sample from the GP conditional distribution
idata.extend(pm.sample_posterior_predictive(idata, var_names=["f_pred"]))
Sampling: [f_pred]
fig = plt.figure(figsize=(10, 4))
ax = fig.gca()
f_pred = az.extract(idata.posterior_predictive, var_names="f_pred").transpose("sample", ...)
plot_gp_dist(ax, f_pred, X_new)
ax.plot(X, f_true, "dodgerblue", lw=3, label="True generating function 'f'")
ax.plot(X, y, "ok", ms=3, label="Observed data")
ax.set_xlabel("X")
ax.set_ylabel("True f(x)")
ax.set_title("Conditional distribution of f_*, given f")
plt.legend();
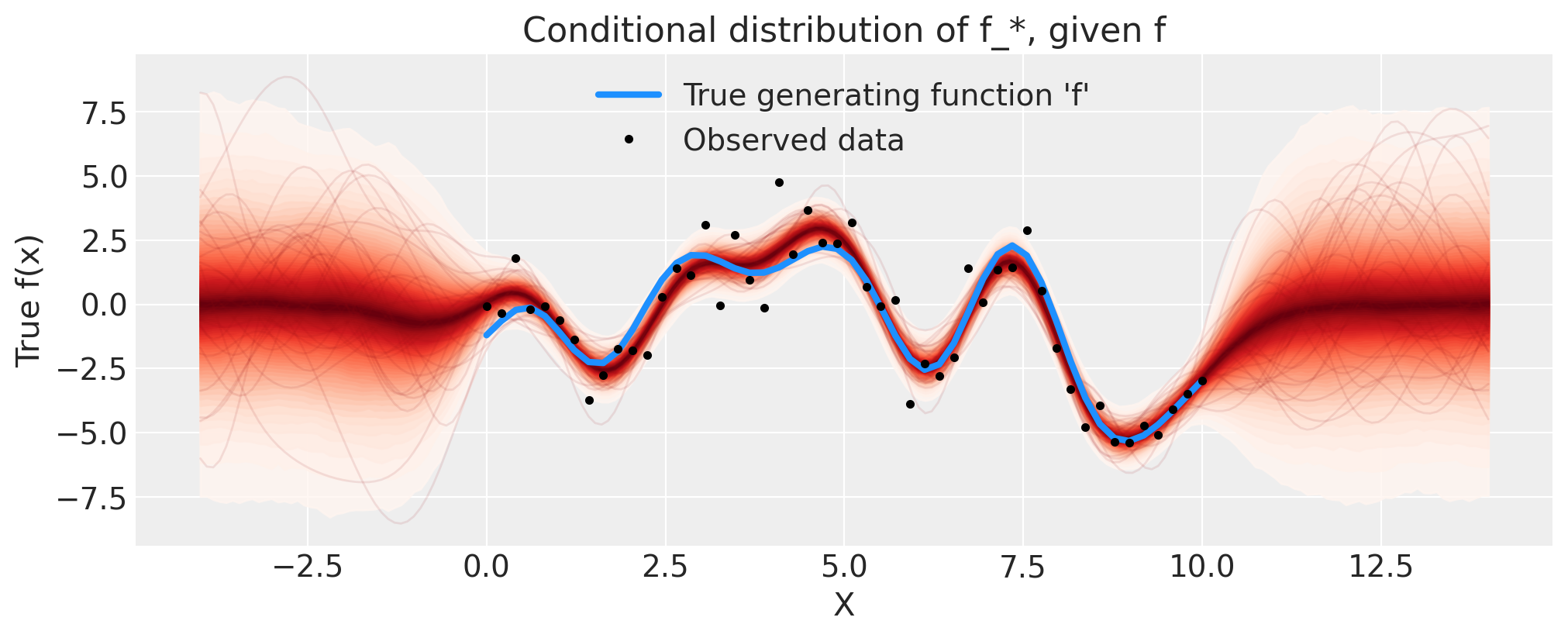
示例 2:分类#
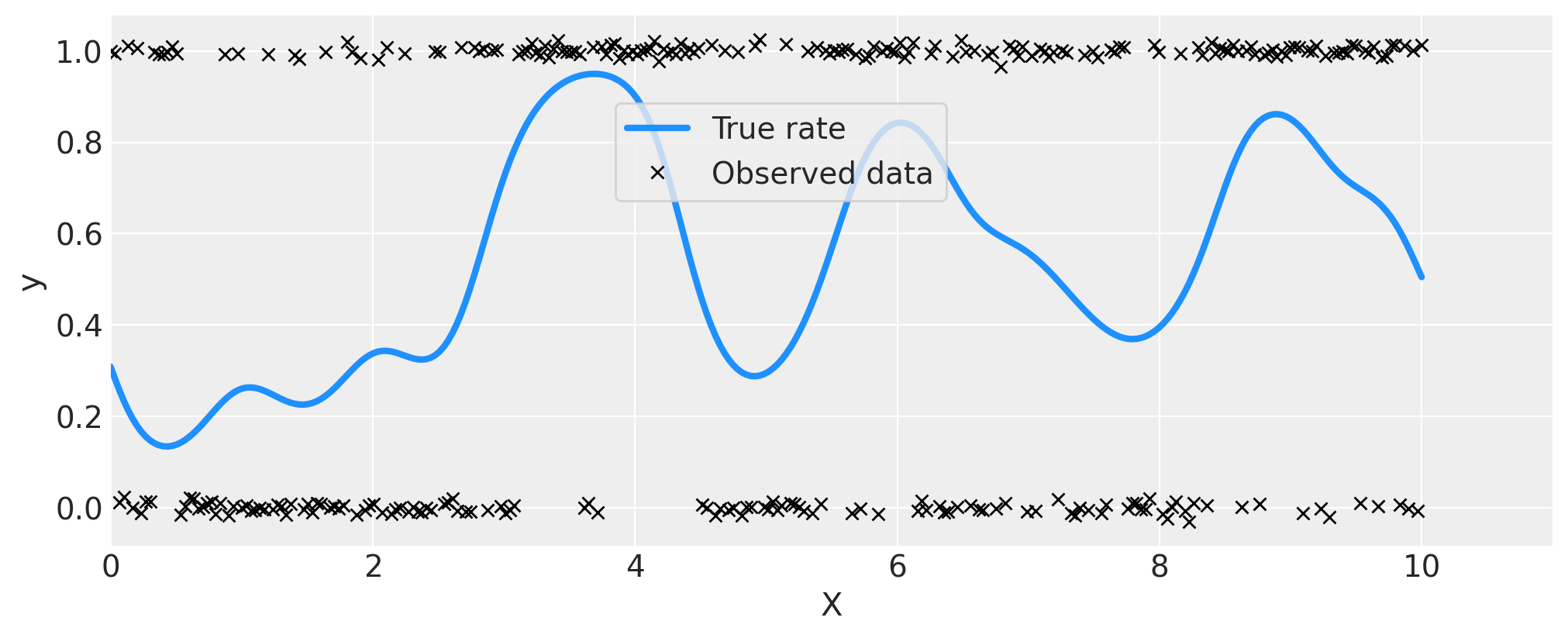
首先我们使用一个GP来生成一些符合伯努利分布的数据,其中\(p\),即出现1而不是0的概率,是\(x\)的函数。我重置了种子并添加了更多的假数据点,因为对于模型来说,在观测较少的情况下,区分0.5附近的变异可能会很困难。
# reset the random seed for the new example
RANDOM_SEED = 8888
rng = np.random.default_rng(RANDOM_SEED)
# number of data points
n = 300
# x locations
x = np.linspace(0, 10, n)
# true covariance
ell_true = 0.5
eta_true = 1.0
cov_func = eta_true**2 * pm.gp.cov.ExpQuad(1, ell_true)
K = cov_func(x[:, None]).eval()
# zero mean function
mean = np.zeros(n)
# sample from the gp prior
f_true = pm.draw(pm.MvNormal.dist(mu=mean, cov=K), 1, random_seed=rng)
# Sample the GP through the likelihood
y = pm.Bernoulli.dist(p=pm.math.invlogit(f_true)).eval()
fig = plt.figure(figsize=(10, 4))
ax = fig.gca()
ax.plot(x, pm.math.invlogit(f_true).eval(), "dodgerblue", lw=3, label="True rate")
# add some noise to y to make the points in the plot more visible
ax.plot(x, y + np.random.randn(n) * 0.01, "kx", ms=6, label="Observed data")
ax.set_xlabel("X")
ax.set_ylabel("y")
ax.set_xlim([0, 11])
plt.legend(loc=(0.35, 0.65), frameon=True);
with pm.Model() as model:
ell = pm.InverseGamma("ell", mu=1.0, sigma=0.5)
eta = pm.Exponential("eta", lam=1.0)
cov = eta**2 * pm.gp.cov.ExpQuad(1, ell)
gp = pm.gp.Latent(cov_func=cov)
f = gp.prior("f", X=x[:, None])
# logit link and Bernoulli likelihood
p = pm.Deterministic("p", pm.math.invlogit(f))
y_ = pm.Bernoulli("y", p=p, observed=y)
idata = pm.sample(1000, chains=2, cores=2, nuts_sampler="numpyro")
We recommend running at least 4 chains for robust computation of convergence diagnostics
# check Rhat, values above 1 may indicate convergence issues
n_nonconverged = int(np.sum(az.rhat(idata)[["eta", "ell", "f_rotated_"]].to_array() > 1.03).values)
if n_nonconverged == 0:
print("No Rhat values above 1.03, \N{check mark}")
else:
print(f"The MCMC chains for {n_nonconverged} RVs appear not to have converged.")
No Rhat values above 1.03, ✓
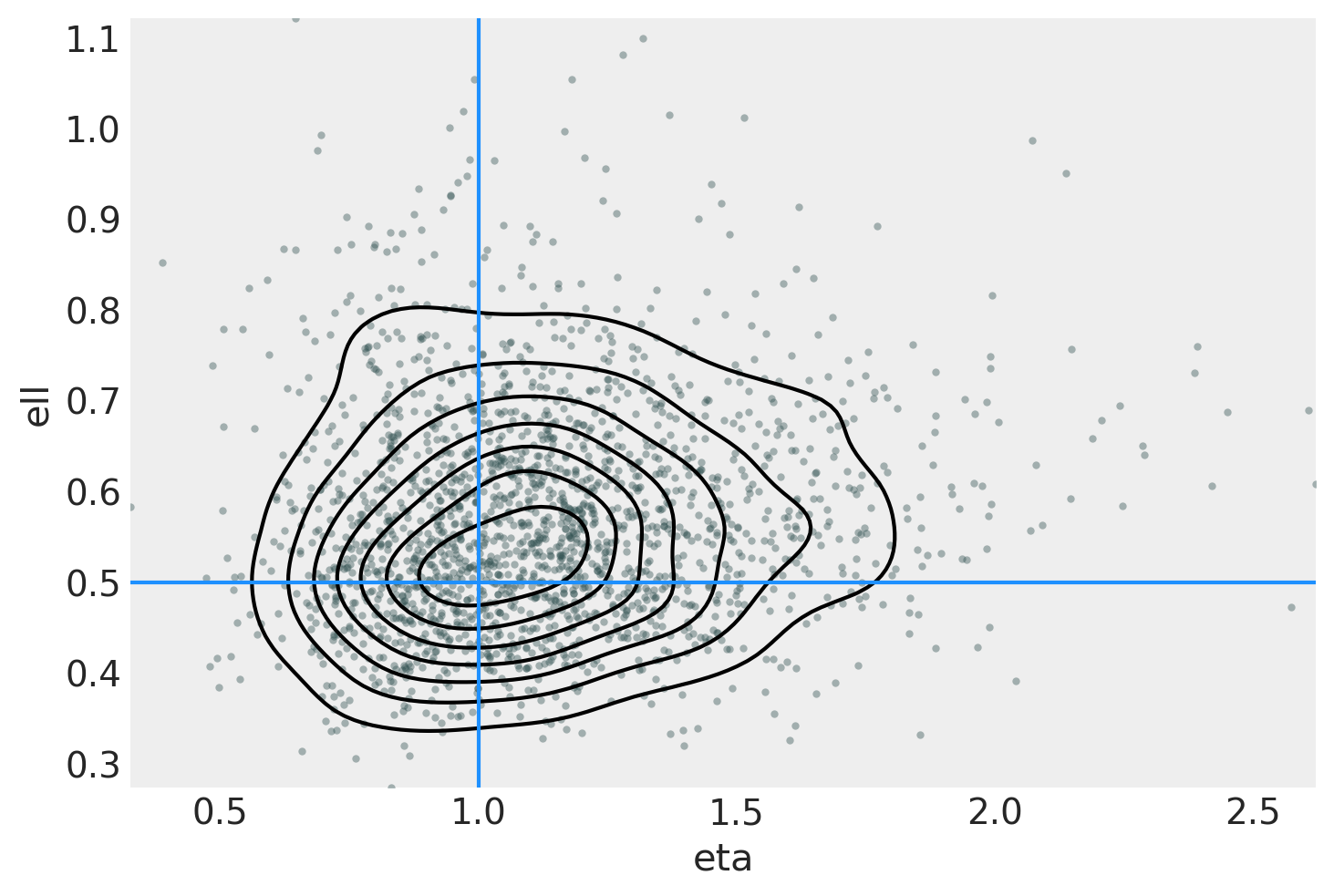
ax = az.plot_pair(
idata,
var_names=["eta", "ell"],
kind=["kde", "scatter"],
scatter_kwargs={"color": "darkslategray", "alpha": 0.4},
gridsize=25,
divergences=True,
)
ax.axvline(x=eta_true, color="dodgerblue")
ax.axhline(y=ell_true, color="dodgerblue");
n_pred = 200
X_new = np.linspace(0, 12, n_pred)[:, None]
with model:
f_pred = gp.conditional("f_pred", X_new, jitter=1e-4)
p_pred = pm.Deterministic("p_pred", pm.math.invlogit(f_pred))
with model:
idata.extend(pm.sample_posterior_predictive(idata.posterior, var_names=["f_pred", "p_pred"]))
Sampling: [f_pred]
# plot the results
fig = plt.figure(figsize=(10, 4))
ax = fig.gca()
# plot the samples from the gp posterior with samples and shading
p_pred = az.extract(idata.posterior_predictive, var_names="p_pred").transpose("sample", ...)
plot_gp_dist(ax, p_pred, X_new)
# plot the data (with some jitter) and the true latent function
plt.plot(x, pm.math.invlogit(f_true).eval(), "dodgerblue", lw=3, label="True f")
plt.plot(
x,
y + np.random.randn(y.shape[0]) * 0.01,
"kx",
ms=6,
alpha=0.5,
label="Observed data",
)
# axis labels and title
plt.xlabel("X")
plt.ylabel("True f(x)")
plt.xlim([0, 12])
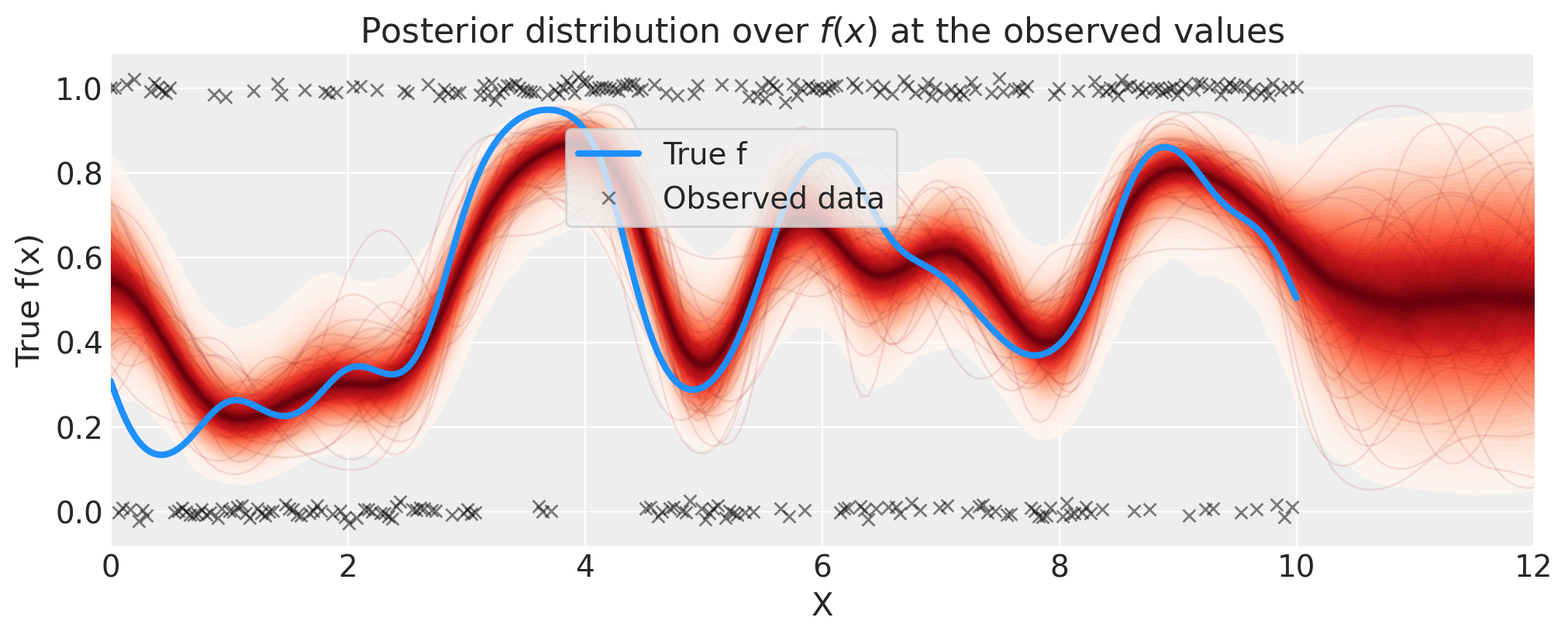
plt.title("Posterior distribution over $f(x)$ at the observed values")
plt.legend(loc=(0.32, 0.65), frameon=True);
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray
Last updated: Mon May 27 2024
Python implementation: CPython
Python version : 3.12.2
IPython version : 8.22.2
pytensor: 2.20.0
aeppl : not installed
xarray : 2024.3.0
matplotlib: 3.8.3
numpy : 1.26.4
pymc : 5.15.0+14.gfd11cf012
arviz : 0.17.1
Watermark: 2.4.3