均值和协方差函数#

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor.tensor as pt

%config InlineBackend.figure_format = "retina"

WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = (10, 4)

PyMC 中提供了大量均值和协方差函数。定义自定义的均值和协方差函数相对容易。由于 PyMC 使用 PyTensor，因此用户不需要定义它们的梯度。

均值函数#

以下均值函数在 PyMC 中可用。

所有遵循相似的使用模式。首先，指定均值函数。然后可以在某些输入上进行评估。前两个均值函数非常简单。无论输入如何，gp.mean.Zero 返回一个与输入值数量相同长度的零向量。

零#

zero_func = pm.gp.mean.Zero()

X = np.linspace(0, 1, 5)[:, None]
print(zero_func(X).eval())

[0. 0. 0. 0. 0.]

PyMC中所有GP实现的默认均值函数是零。

常量#

gp.mean.Constant 返回一个值为提供的向量。

const_func = pm.gp.mean.Constant(25.2)

print(const_func(X).eval())

[25.2 25.2 25.2 25.2 25.2]

只要形状与它将接收的输入匹配，gp.mean.Constant 也可以接受 PyTensor 张量或 PyMC 随机变量的向量。

const_func_vec = pm.gp.mean.Constant(pt.ones(5))

print(const_func_vec(X).eval())

[1. 1. 1. 1. 1.]

线性#

gp.mean.Linear 是一个接受系数矩阵和截距向量（或在一维情况下接受斜率和标量截距）作为输入的函数。

beta = rng.normal(size=3)
b = 0.0

lin_func = pm.gp.mean.Linear(coeffs=beta, intercept=b)

X = rng.normal(size=(5, 3))
print(lin_func(X).eval())

[ 1.03424803 -2.25903687  0.78030931  0.9880038  -3.45565466]

定义自定义均值函数#

要定义一个自定义的均值函数，可以继承 gp.mean.Mean，并提供 __call__ 和 __init__ 方法。例如，Constant 均值函数的代码如下

import theano.tensor as tt

class Constant(pm.gp.mean.Mean):
    
    def __init__(self, c=0):
        Mean.__init__(self)
        self.c = c 

    def __call__(self, X): 
        return tt.alloc(1.0, X.shape[0]) * self.c

请记住，必须使用 PyTensor 而不是 NumPy。

协方差函数#

PyMC 包含了一系列更丰富的 内置 协方差 函数。 以下展示了从具有给定协方差函数的 GP 先验中抽取的函数，并演示了如何使用 Python 运算符以直接的方式构建复合协方差函数。 我们的目标是使我们的 API 尽可能地遵循核代数（参见 Rasmussen 和 Williams [2006] 的第 4 章）。 请参阅主要文档页面以了解它们在 PyMC 中的使用概述。

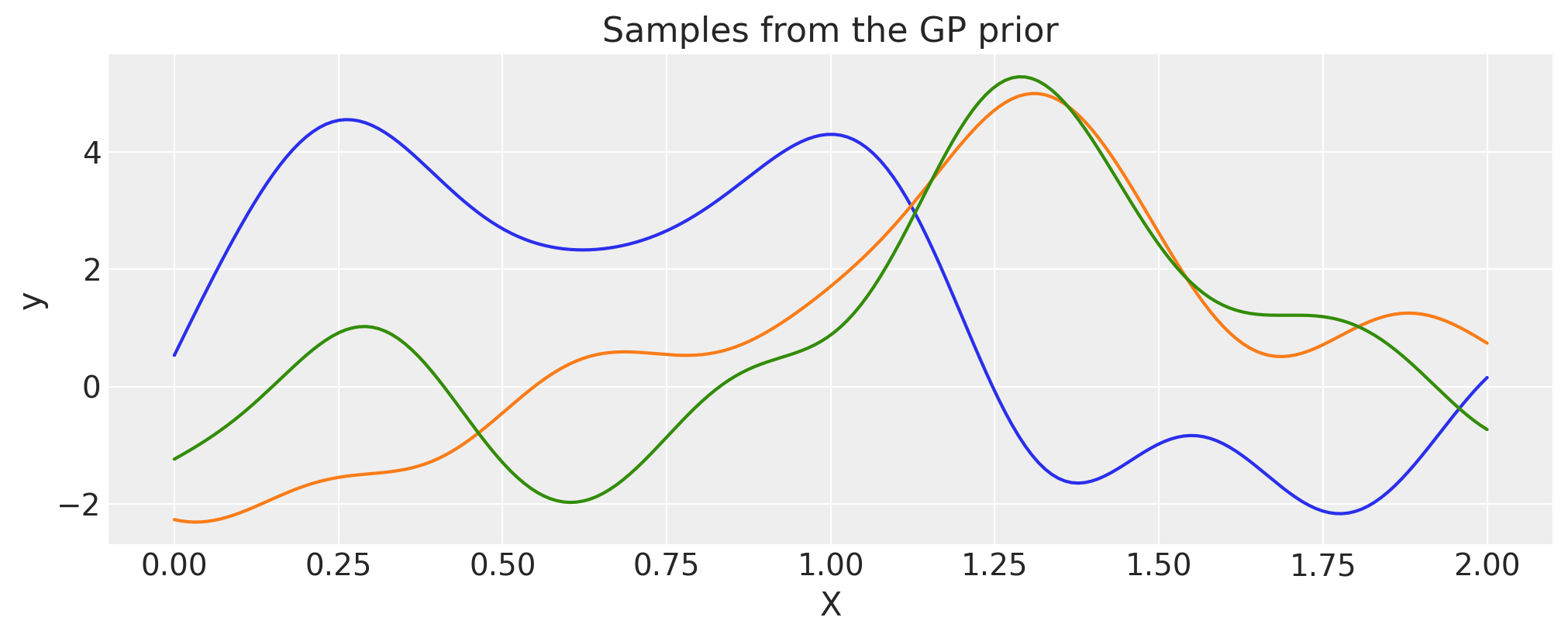
指数二次方#

\[ k(x, x') = \mathrm{exp}\left[ -\frac{(x - x')^2}{2 \ell^2} \right] \]
lengthscale = 0.2
eta = 2.0
cov = eta**2 * pm.gp.cov.ExpQuad(1, lengthscale)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(
        pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=K.shape[0]), draws=3, random_seed=rng
    ).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/b32dad0edc3b59a6dc6f0da44044b002c11ab9c4e4995b8158637bd766cfad51.png

二维（及更高维）输入#

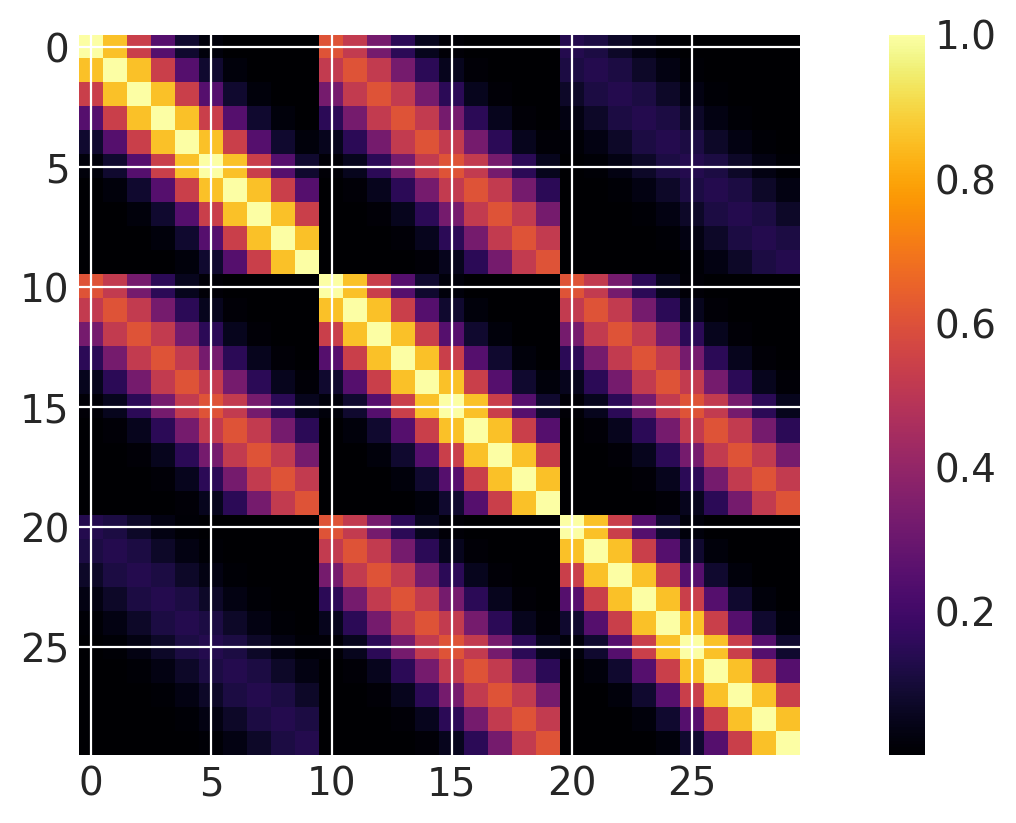
两个维度均激活#

定义具有高维输入的核很容易。请注意，ls（长度尺度）参数是一个长度为2的数组。PyMC随机变量的列表可以用于自动相关性确定（ARD）。

x1 = np.linspace(0, 1, 10)
x2 = np.arange(1, 4)
# Cartesian product
X2 = np.dstack(np.meshgrid(x1, x2)).reshape(-1, 2)

ls = np.array([0.2, 1.0])
cov = pm.gp.cov.ExpQuad(input_dim=2, ls=ls)

m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);
../../../_images/02929fba768b922f0db9de2c1599cbcdd4f1625cc961098d57c172b5ca2ee514.png

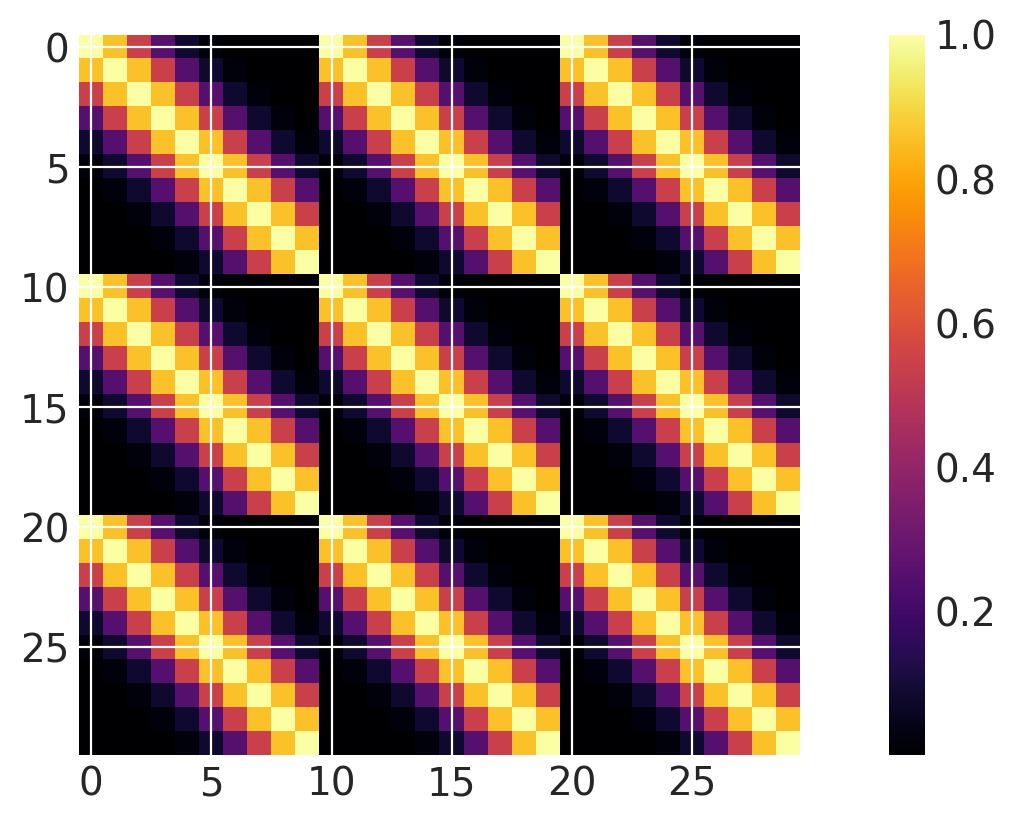
一维活动#

ls = 0.2
cov = pm.gp.cov.ExpQuad(input_dim=2, ls=ls, active_dims=[0])

m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);
../../../_images/12b97e2a173a6b128fea67ff752b04bab1c8917cc633ba568ae432d047d6e3d4.png

不同维度上协方差乘积#

请注意，这相当于使用一个二维的 ExpQuad，并为每个维度使用单独的长度尺度参数。

ls1 = 0.2
ls2 = 1.0
cov1 = pm.gp.cov.ExpQuad(2, ls1, active_dims=[0])
cov2 = pm.gp.cov.ExpQuad(2, ls2, active_dims=[1])
cov = cov1 * cov2

m = plt.imshow(cov(X2).eval(), cmap="inferno", interpolation="none")
plt.colorbar(m);
../../../_images/02929fba768b922f0db9de2c1599cbcdd4f1625cc961098d57c172b5ca2ee514.png

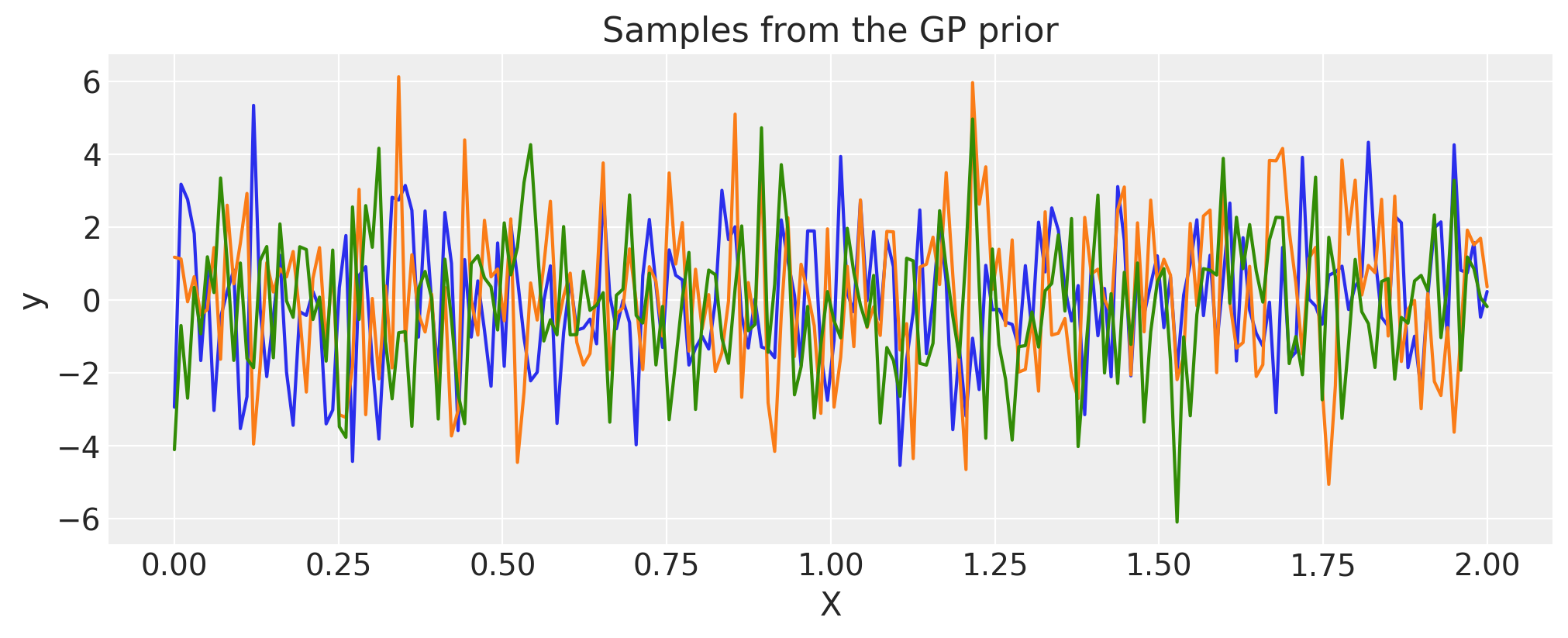
白噪声#

\[ k(x, x') = \sigma^2 \mathrm{I}_{xx} \]
sigma = 2.0
cov = pm.gp.cov.WhiteNoise(sigma)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/500414d8ae4ba779eda2be5fe1788a15b72a13b3f8d284a2e1cd93726b5c8a79.png

常量#

\[ k(x, x') = c \]
c = 2.0
cov = pm.gp.cov.Constant(c)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/6f4a4b018ef99b0c5d2d040a12203f609e8f2fa6ac7474638ac4384cf493d374.png

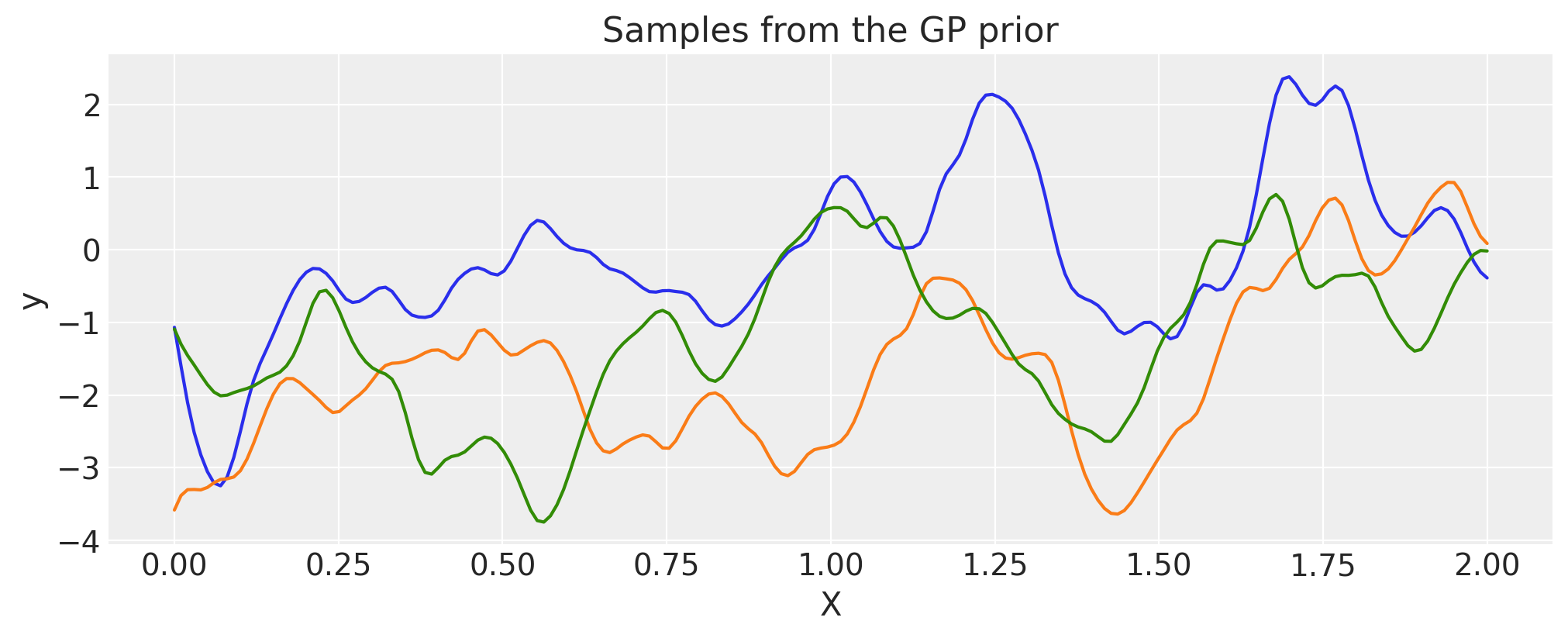
有理二次#

\[ k(x, x') = \left(1 + \frac{(x - x')^2}{2\alpha\ell^2} \right)^{-\alpha} \]
alpha = 0.1
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.RatQuad(1, ls, alpha)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/d6f8b1dd0fa3fae3925caa95e92e51ea502f3b29c71184a0316fead2a3529f30.png

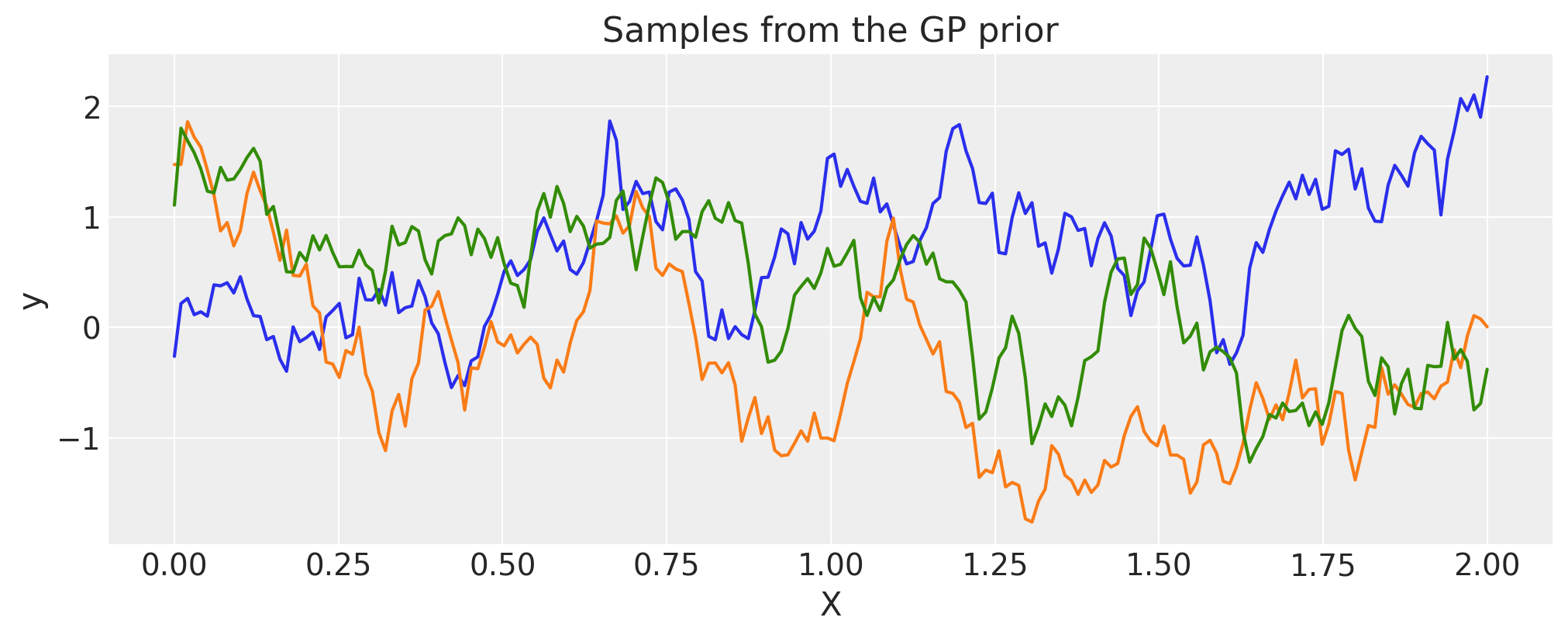
指数#

\[ k(x, x') = \mathrm{exp}\left[ -\frac{||x - x'||}{2\ell^2} \right] \]
inverse_lengthscale = 5
cov = pm.gp.cov.Exponential(1, ls_inv=inverse_lengthscale)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/5ea3b84aa82fe06fcb7c54511531c3fc18739f82629a05057f90b60fcf1a83d0.png

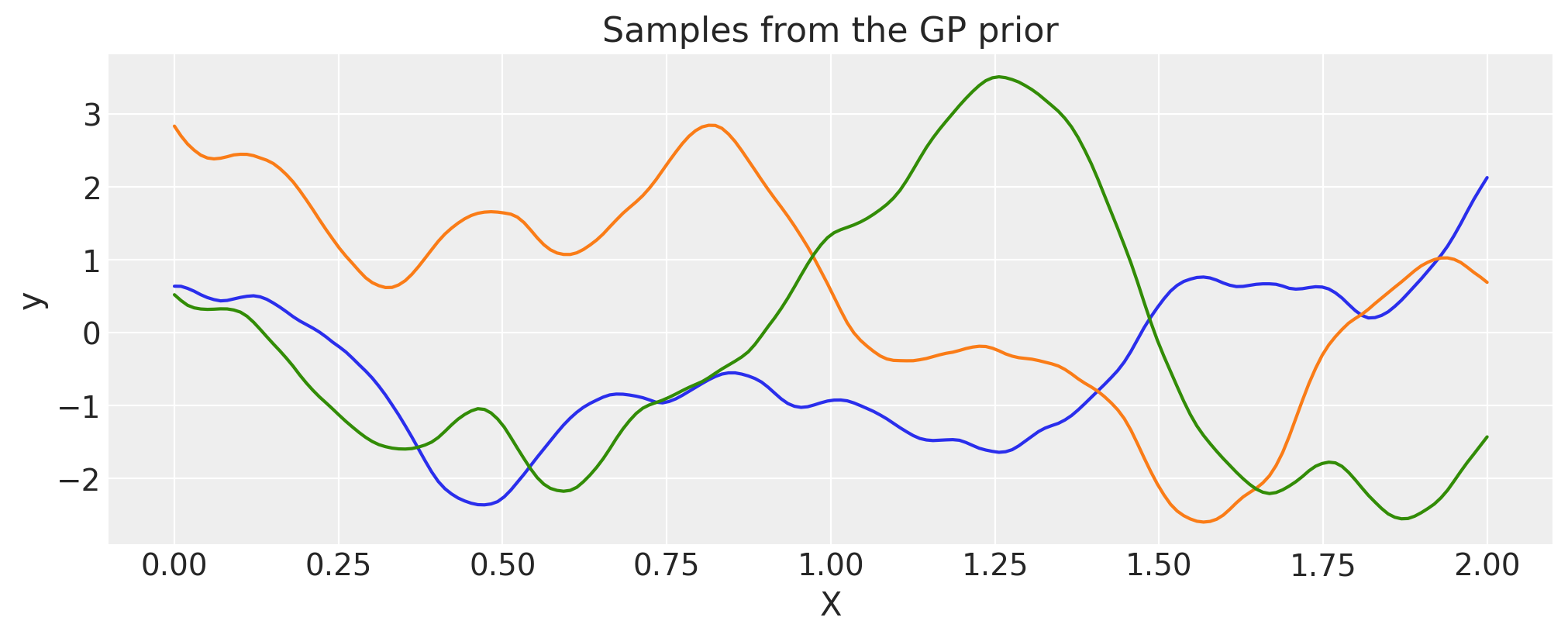
Matern 5/2#

\[ k(x, x') = \left(1 + \frac{\sqrt{5(x - x')^2}}{\ell} + \frac{5(x-x')^2}{3\ell^2}\right) \mathrm{exp}\left[ - \frac{\sqrt{5(x - x')^2}}{\ell} \right] \]
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern52(1, ls)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/1b345944b2480a075afffbe317e1defb18629231e0f1ead08ecfa45fd8aefcc9.png

Matern 3/2#

\[ k(x, x') = \left(1 + \frac{\sqrt{3(x - x')^2}}{\ell}\right) \mathrm{exp}\left[ - \frac{\sqrt{3(x - x')^2}}{\ell} \right] \]
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern32(1, ls)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
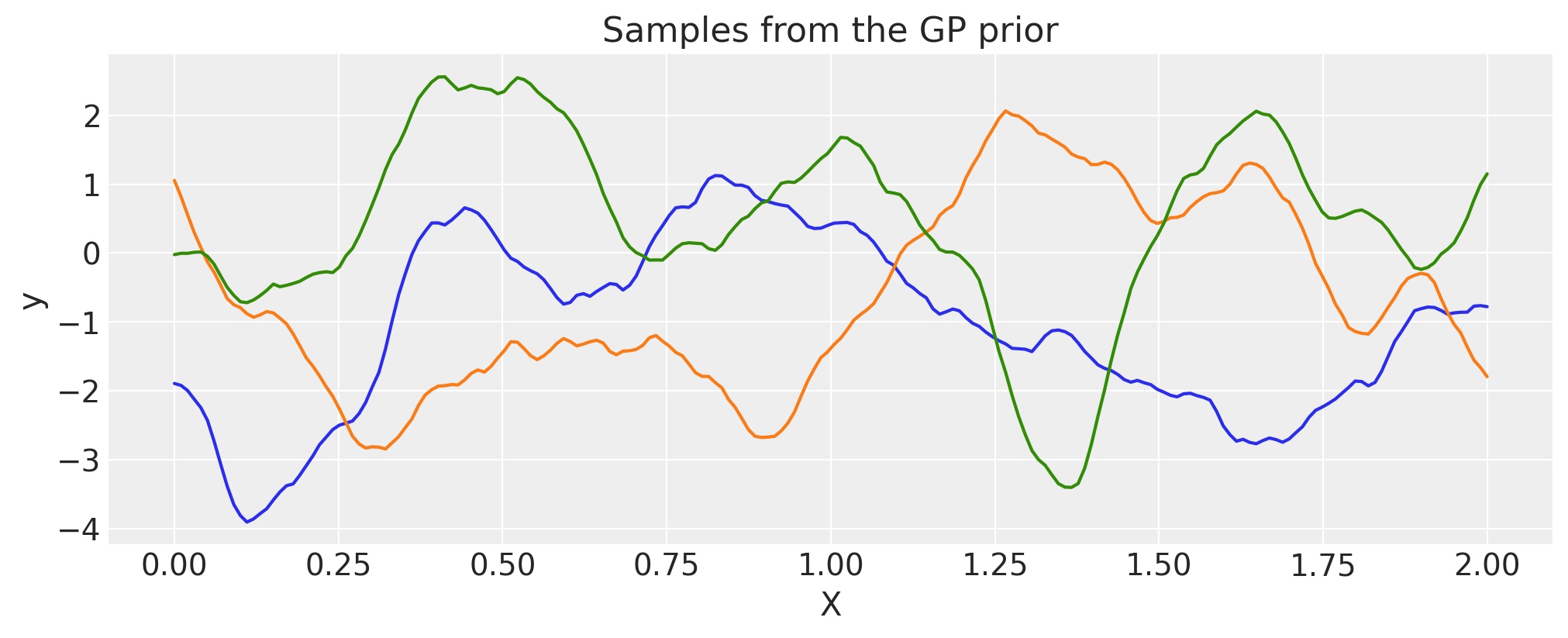
../../../_images/8f165b1cd6e165553793e18b94fcedc6ee6a879963dcc0a889a740a92449099d.png

Matern 1/2#

\[k(x, x') = \mathrm{exp}\left[ -\frac{(x - x')^2}{\ell} \right]\]
ls = 0.2
tau = 2.0
cov = tau * pm.gp.cov.Matern12(1, ls)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
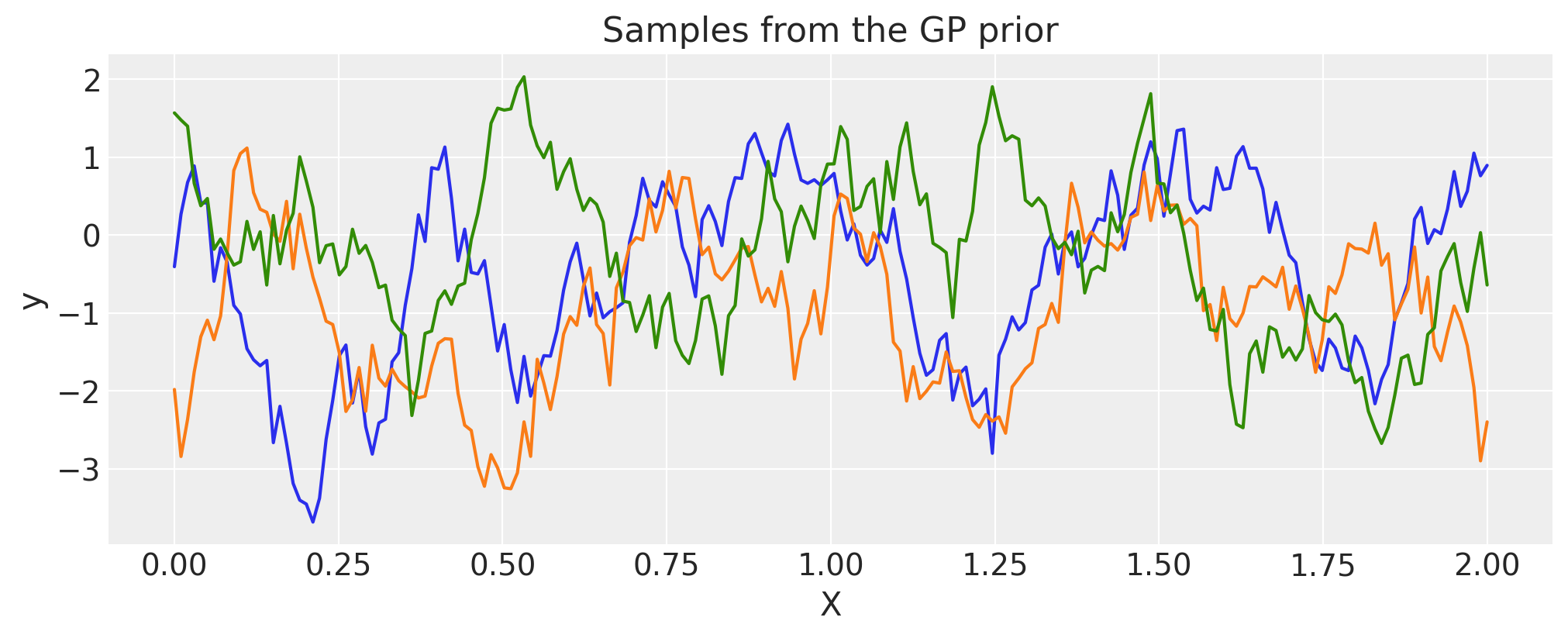
../../../_images/ed76843d12dfd9f1db980d4daf441fc6555706b75a2627a32e83124a8bbc8bfa.png

余弦#

\[ k(x, x') = \mathrm{cos}\left( 2 \pi \frac{||x - x'||}{ \ell^2} \right) \]
period = 0.5
cov = pm.gp.cov.Cosine(1, period)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-4)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
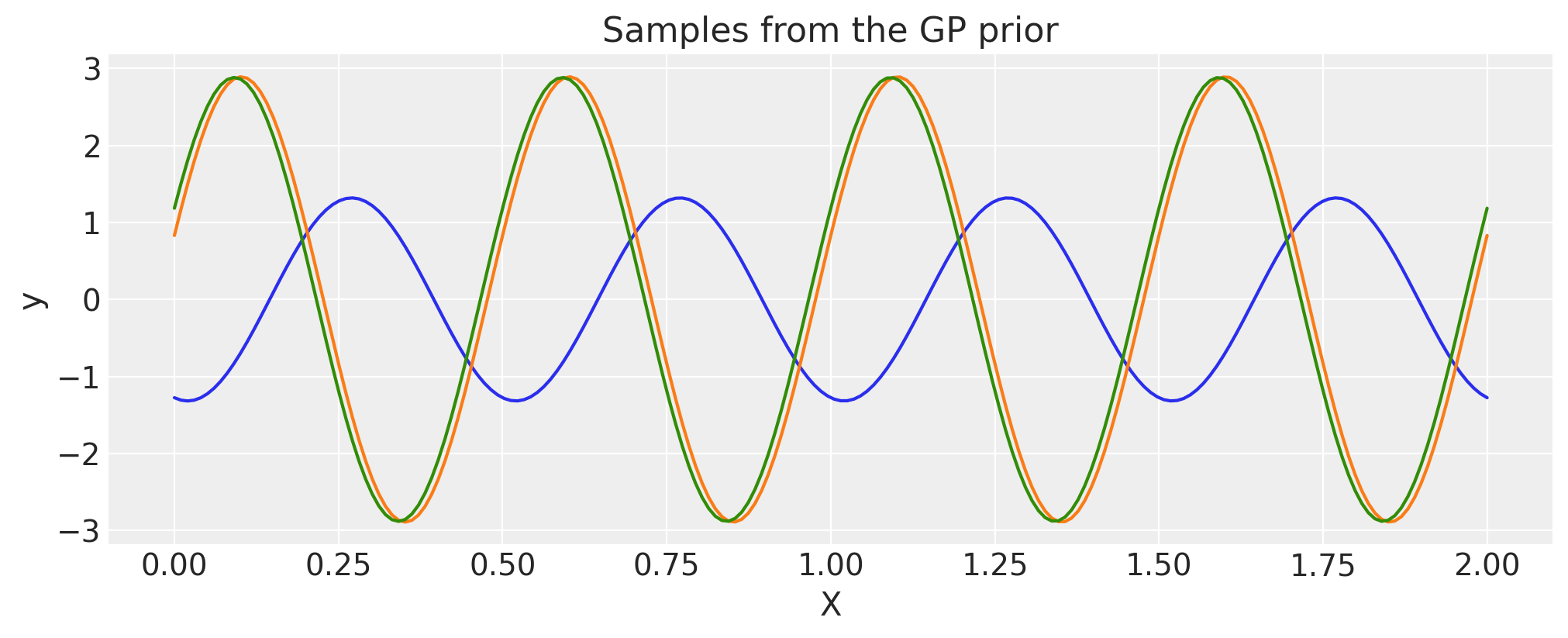
../../../_images/8e4787d3f82349aef3c5df155d63317fa1c1e353c4f87a0579689406a21d15fd.png

线性#

\[ k(x, x') = (x - c)(x' - c) \]
c = 1.0
tau = 2.0
cov = tau * pm.gp.cov.Linear(1, c)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
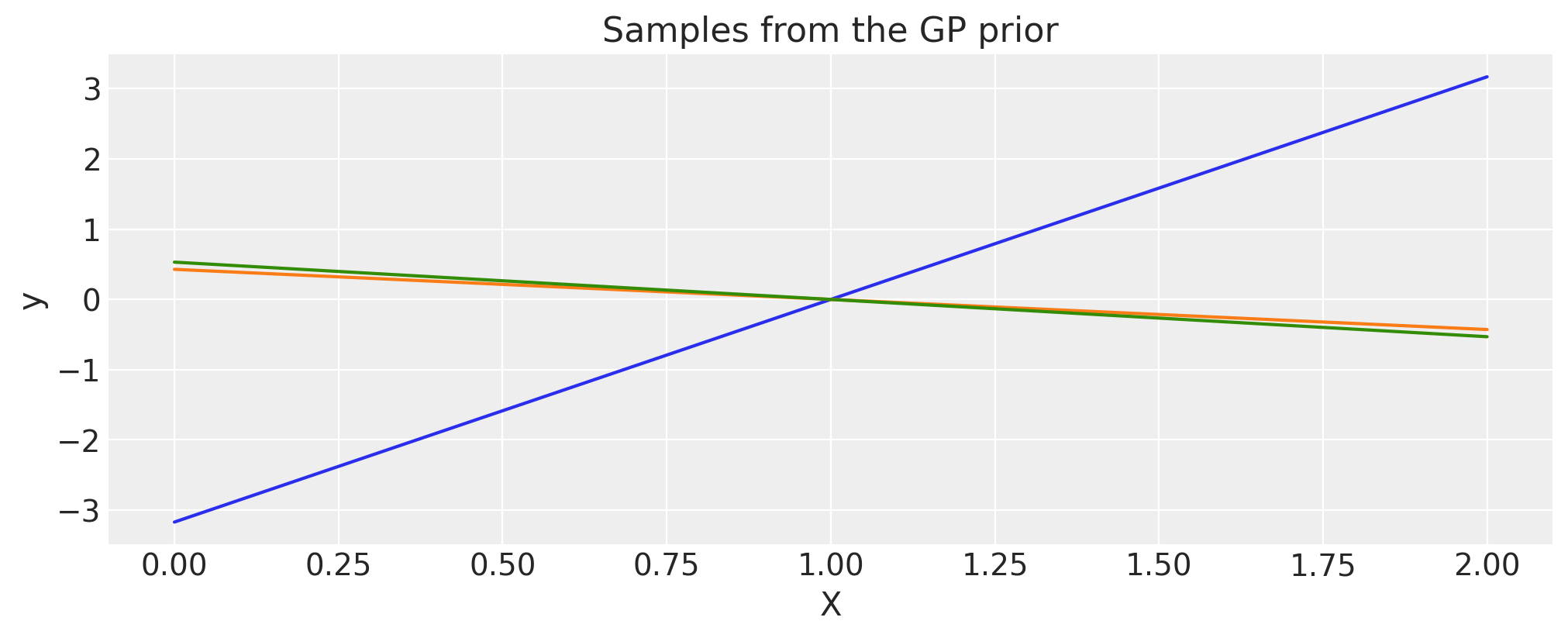
../../../_images/c90bfbfc82b41ed9b678970725e9f9bf9fa471bf1e1f0307efb2c5d559691747.png

多项式#

\[ k(x, x') = [(x - c)(x' - c) + \mathrm{offset}]^{d} \]
c = 1.0
d = 3
offset = 1.0
tau = 0.1
cov = tau * pm.gp.cov.Polynomial(1, c=c, d=d, offset=offset)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
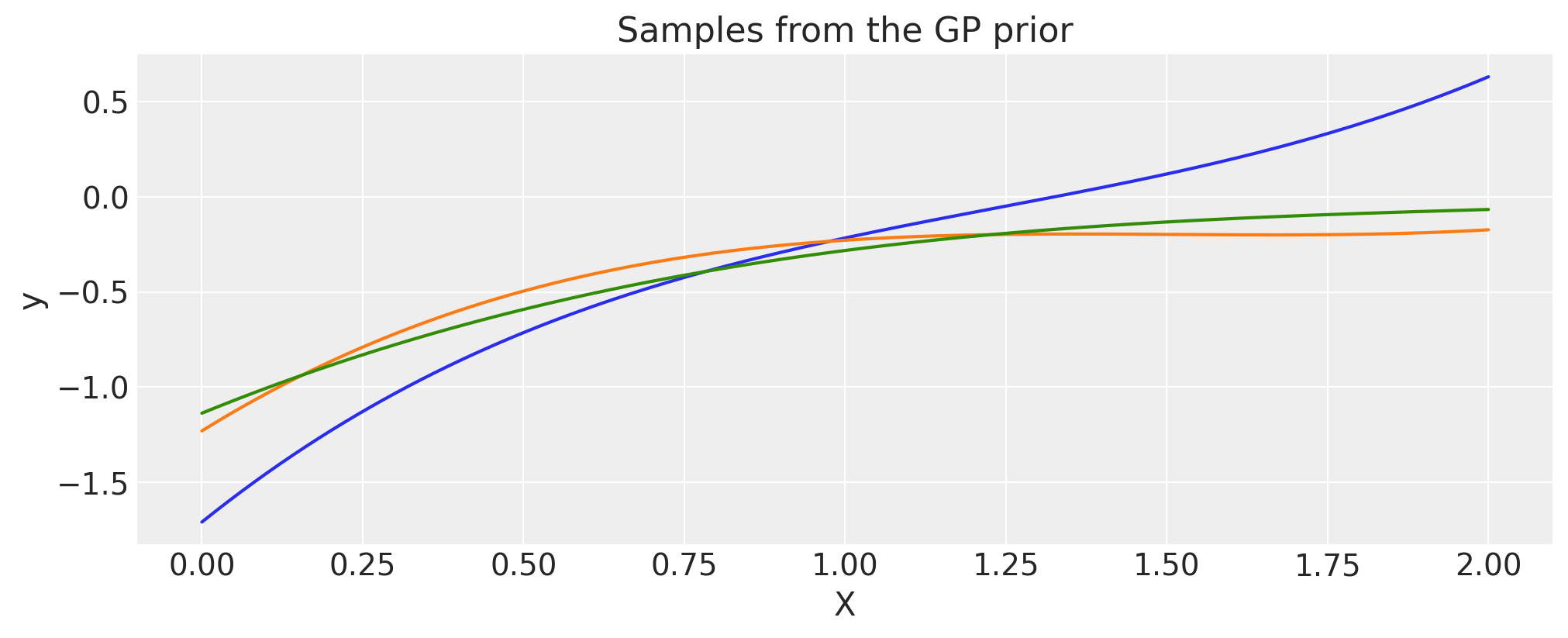
../../../_images/d8cd362b8bce0e258bba3116453249c4ebc4099f8d5cfaff84d7096a5b85425e.png

使用预计算协方差矩阵进行乘法#

协方差函数 cov 可以与 numpy 矩阵 K_cos 相乘，只要形状合适即可。

# first evaluate a covariance function into a matrix
period = 0.2
cov_cos = pm.gp.cov.Cosine(1, period)
K_cos = cov_cos(X).eval()

# now multiply it with a covariance *function*
cov = pm.gp.cov.Matern32(1, 0.5) * K_cos

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
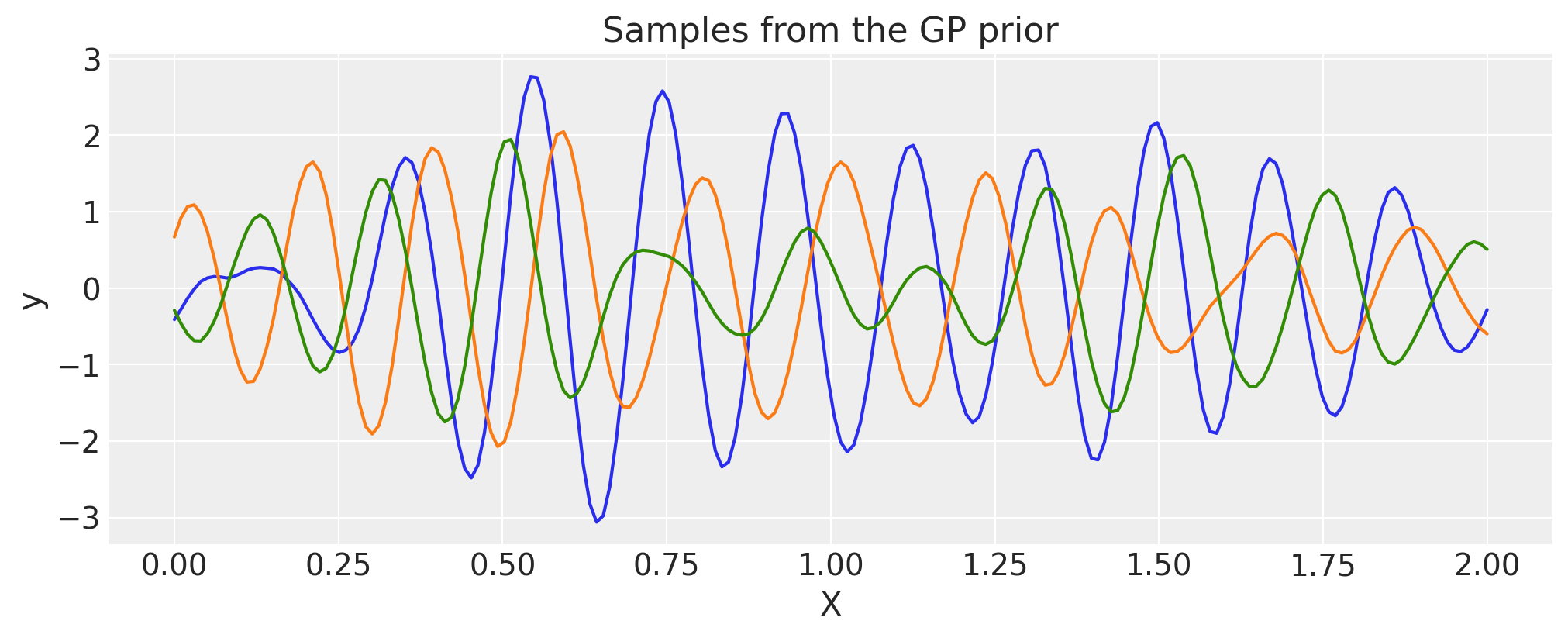
../../../_images/360b5f89d07006361219bcc2b9b44c12f81cba8c4f0cf05df1f2a82a6e18f130.png

对输入应用任意变形函数#

如果 \(k(x, x')\) 是一个有效的协方差函数，那么 \(k(w(x), w(x'))\) 也是一个有效的协方差函数。

扭曲函数的第一个参数必须是输入 X。其余参数可以是任何其他内容，包括随机变量。

def warp_func(x, a, b, c):
    return 1.0 + x + (a * pt.tanh(b * (x - c)))


a = 1.0
b = 5.0
c = 1.0

cov_exp = pm.gp.cov.ExpQuad(1, 0.2)
cov = pm.gp.cov.WarpedInput(1, warp_func=warp_func, args=(a, b, c), cov_func=cov_exp)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 400)[:, None]
wf = warp_func(X.flatten(), a, b, c).eval()

plt.plot(X, wf)
plt.xlabel("X")
plt.ylabel("warp_func(X)")
plt.title("The warping function used")

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
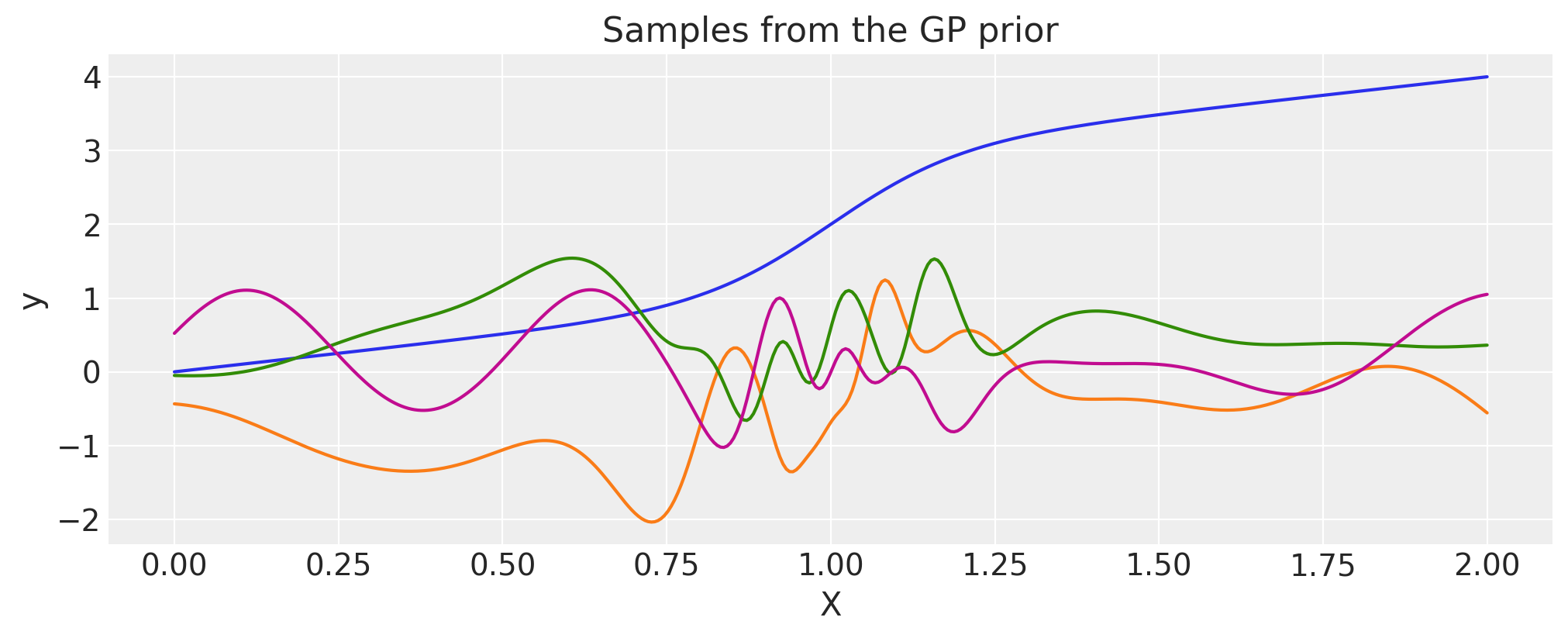
../../../_images/42d54c0850a3fad919c28143f8fab6978d27e2c45203c8bbc81673a54231de2f.png

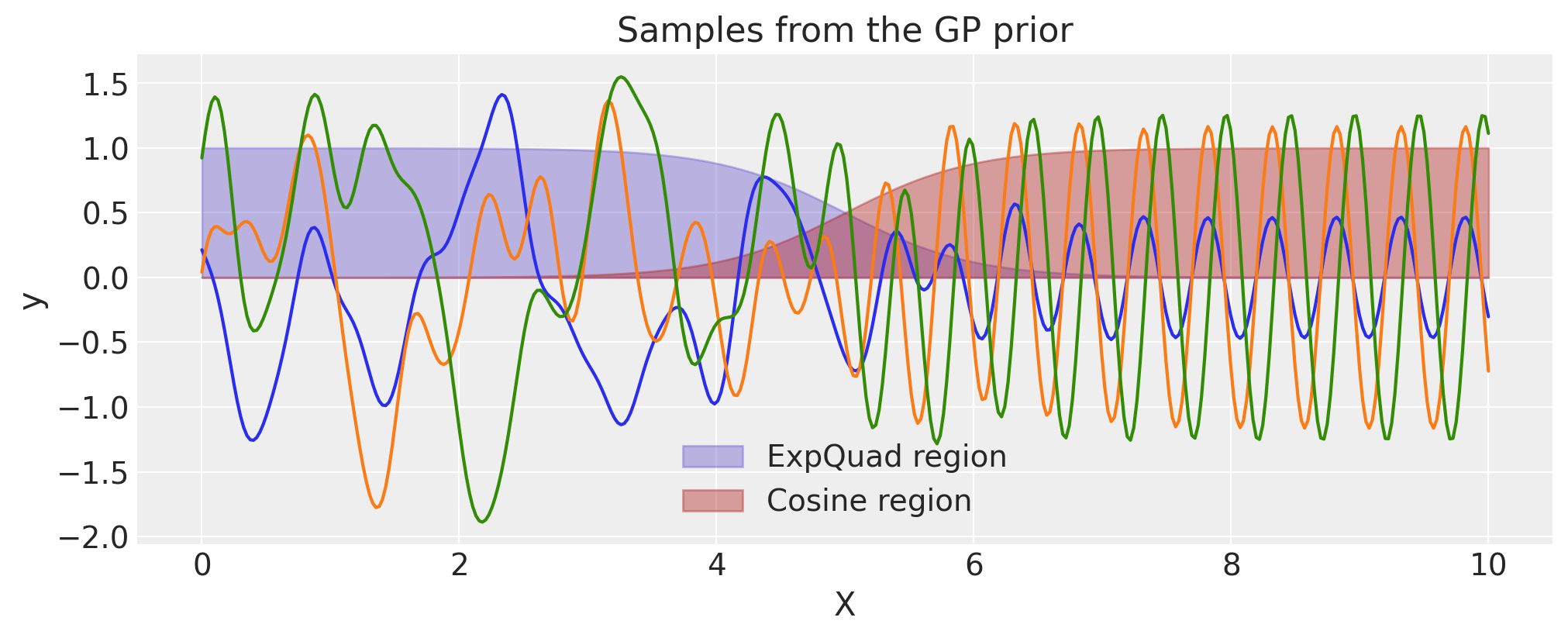
使用WarpedInput构建Periodic#

The WarpedInput 核函数可以用来创建 Periodic 协方差。这种协方差模型用于描述周期性函数，但不是精确的正弦波（如 Cosine 核函数那样）。

周期核由以下公式给出

\[ k(x, x') = \exp\left( -\frac{2 \sin^{2}(\pi |x - x'|\frac{1}{T})}{\ell^2} \right) \]

其中 T 是周期，\(\ell\) 是长度尺度。 它可以通过使用函数 \(\mathbf{u}(x) = (\sin(2\pi x \frac{1}{T})\,, \cos(2 \pi x \frac{1}{T}))\) 对 ExpQuad 核的输入进行变形来推导。 这里我们使用 WarpedInput 核来构建它。

输入 X，在本页顶部定义，长度为2“秒”。我们使用一个周期为 \(0.5\)，这意味着从此GP先验中绘制的函数将在2秒内重复4次。

def mapping(x, T):
    c = 2.0 * np.pi * (1.0 / T)
    u = pt.concatenate((pt.sin(c * x), pt.cos(c * x)), 1)
    return u


T = 0.6
ls = 0.4
# note that the input of the covariance function taking
#    the inputs is 2 dimensional
cov_exp = pm.gp.cov.ExpQuad(2, ls)
cov = pm.gp.cov.WarpedInput(1, cov_func=cov_exp, warp_func=mapping, args=(T,))
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
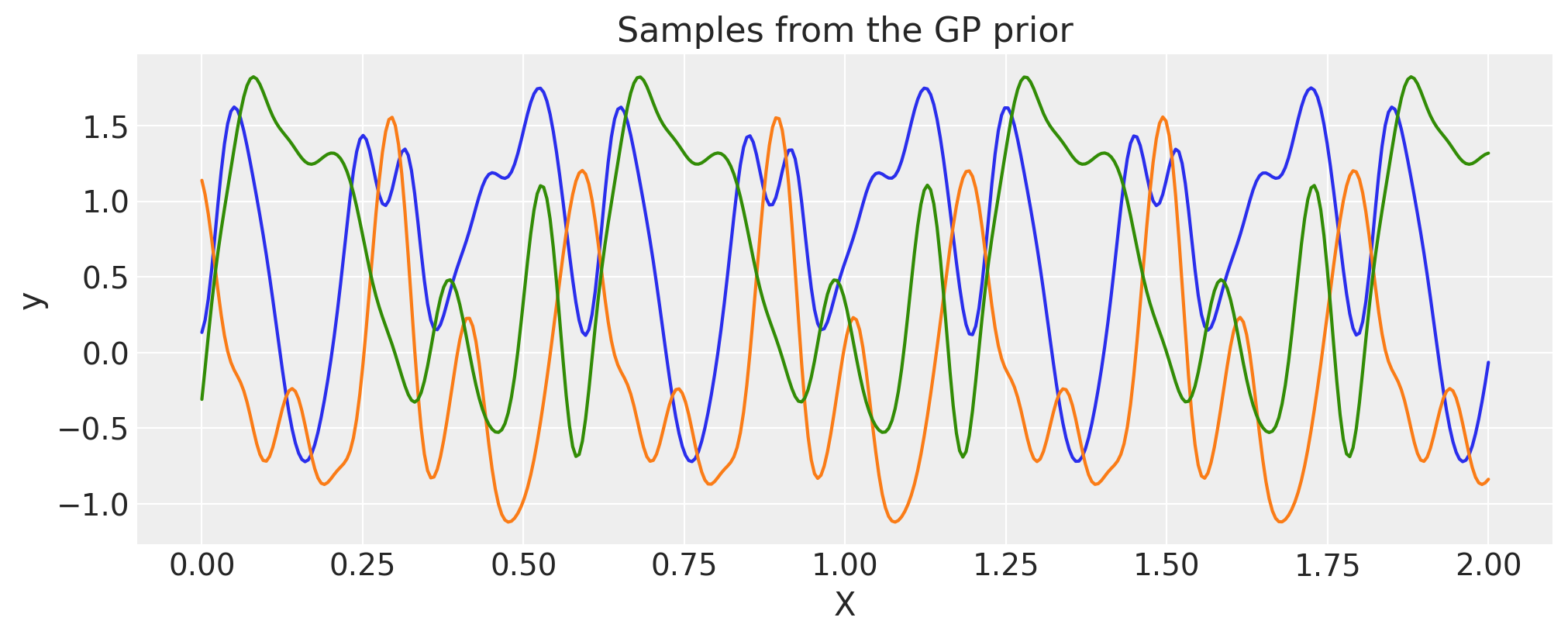
../../../_images/e1c313af0269301db4d821ea64cc4b375b2f562bd104310e9581235180048724.png

周期性#

不需要每次都以这种方式构建周期性协方差。这种协方差函数的一个更高效的实现已经内置了。

period = 0.6
ls = 0.4
cov = pm.gp.cov.Periodic(1, period=period, ls=ls)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
    plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
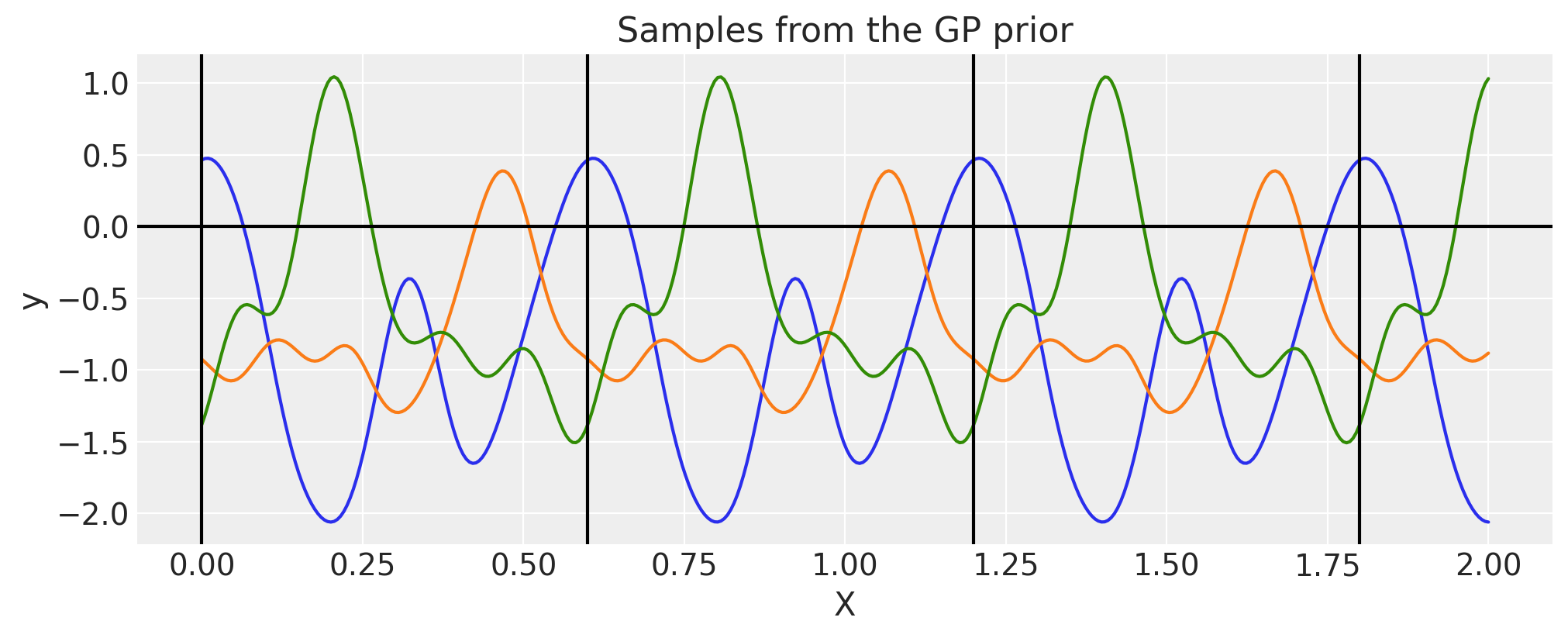
../../../_images/40eaca259ebda4a81144fdc7b28d37d0c8ba38e49bbd593e54f15e325be00715.png

循环#

圆形核与周期性核相似，但具有一个额外的干扰参数 \(\tau\)

在Padonou 和 Roustant [2015]中，Weinland 函数被用于解决问题，并确保在圆形域（不仅仅是）上的正定核。

\[ W_c(t) = \left(1 + \tau \frac{t}{c}\right)\left(1-\frac{t}{c}\right)_+^\tau \]

其中 \(c\) 是 \(t\) 的最大值，而 \(\tau\ge 4\) 是某个正数

用于计算圆上测地距离（弧长）的内核本身看起来像

\[ k_g(x, y) = W_\pi(\text{dist}_{\mathit{geo}}(x, y)) \]

简而言之，你可以认为

  • \(t\) 是时间，它从 \(0\) 运行到 \(24\)，然后回到 \(0\)

  • \(c\) 是任意时间戳之间的最大距离，这里将是 \(12\)

  • \(\tau\) 控制相关性强度，较大的 \(\tau\) 会导致更不光滑的函数

period = 0.6
tau = 4
cov = pm.gp.cov.Circular(1, period=period, tau=tau)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
    plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
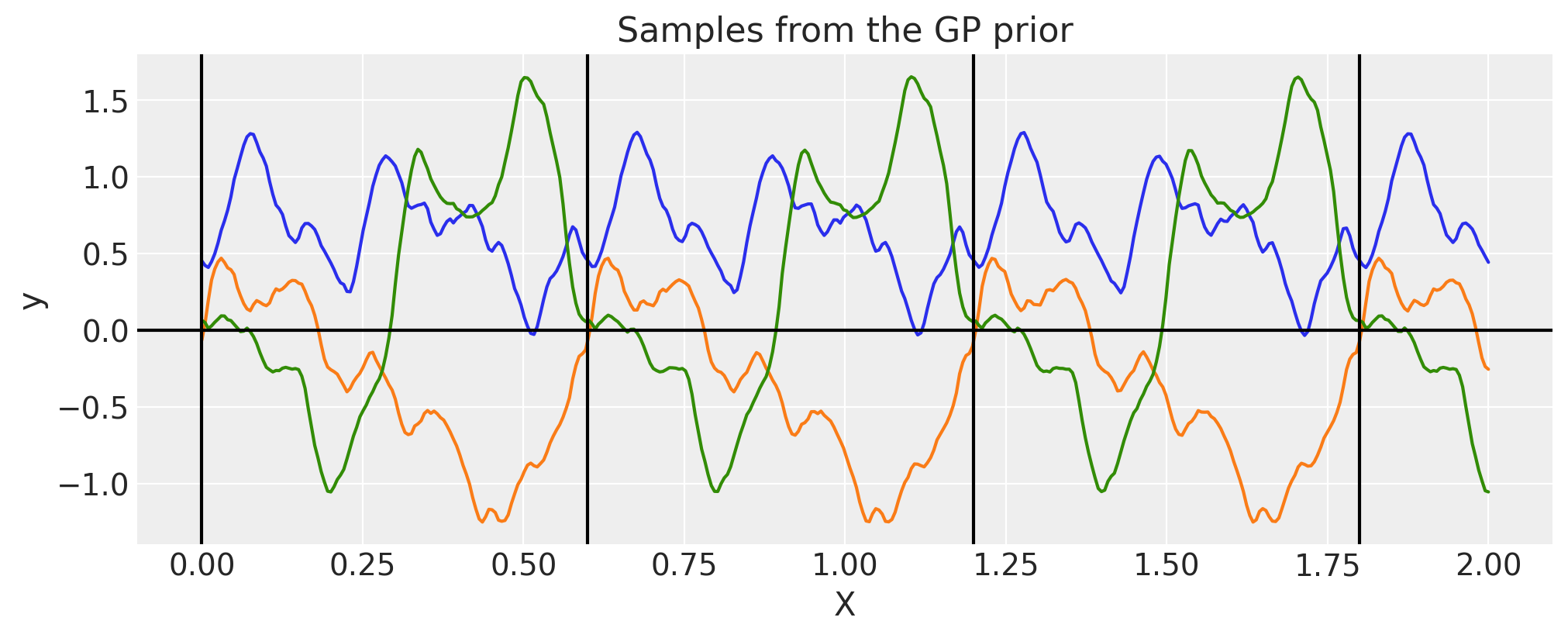
../../../_images/019d297f79d0a03d83aee6e4c1202c5ef63d3b168d97dffd6b19fe5609df721a.png

我们可以看到\(\tau\)的效果，它增加了更多的非平滑模式

period = 0.6
tau = 40
cov = pm.gp.cov.Circular(1, period=period, tau=tau)

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
for p in np.arange(0, 2, period):
    plt.axvline(p, color="black")
plt.axhline(0, color="black")
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
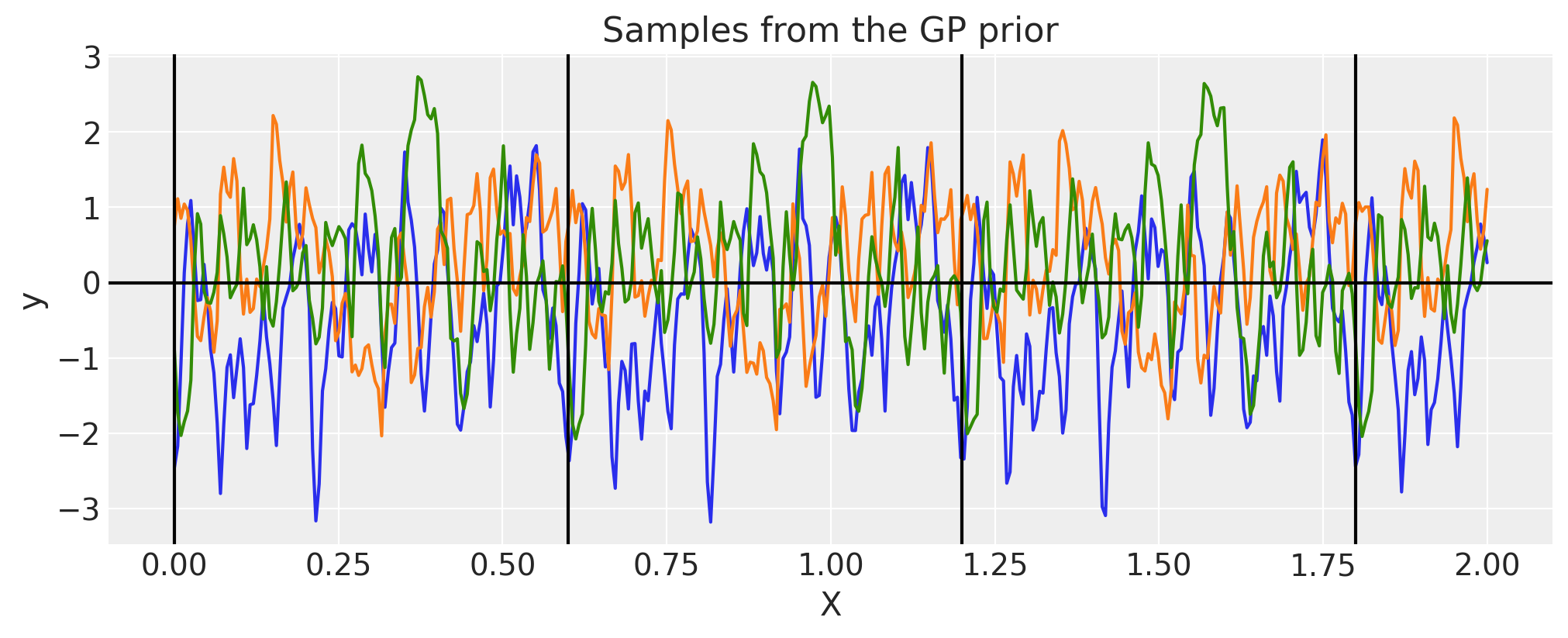
../../../_images/8e9975ae80a3ea7ff3779c9832f7f07a1f62db433c8b4317428db5e7f2c64606.png

吉布斯#

吉布斯协方差函数对长度尺度应用了一个正定扭曲函数。与WarpedInput类似，长度尺度扭曲函数可以通过参数指定，这些参数可以是固定值或随机变量。

def tanh_func(x, ls1, ls2, w, x0):
    """
    ls1: left saturation value
    ls2: right saturation value
    w:   transition width
    x0:  transition location.
    """
    return (ls1 + ls2) / 2.0 - (ls1 - ls2) / 2.0 * pt.tanh((x - x0) / w)


ls1 = 0.05
ls2 = 0.6
w = 0.3
x0 = 1.0
cov = pm.gp.cov.Gibbs(1, tanh_func, args=(ls1, ls2, w, x0))
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

wf = tanh_func(X, ls1, ls2, w, x0).eval()
plt.plot(X, wf)
plt.ylabel("lengthscale")
plt.xlabel("X")
plt.title("Lengthscale as a function of X")

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
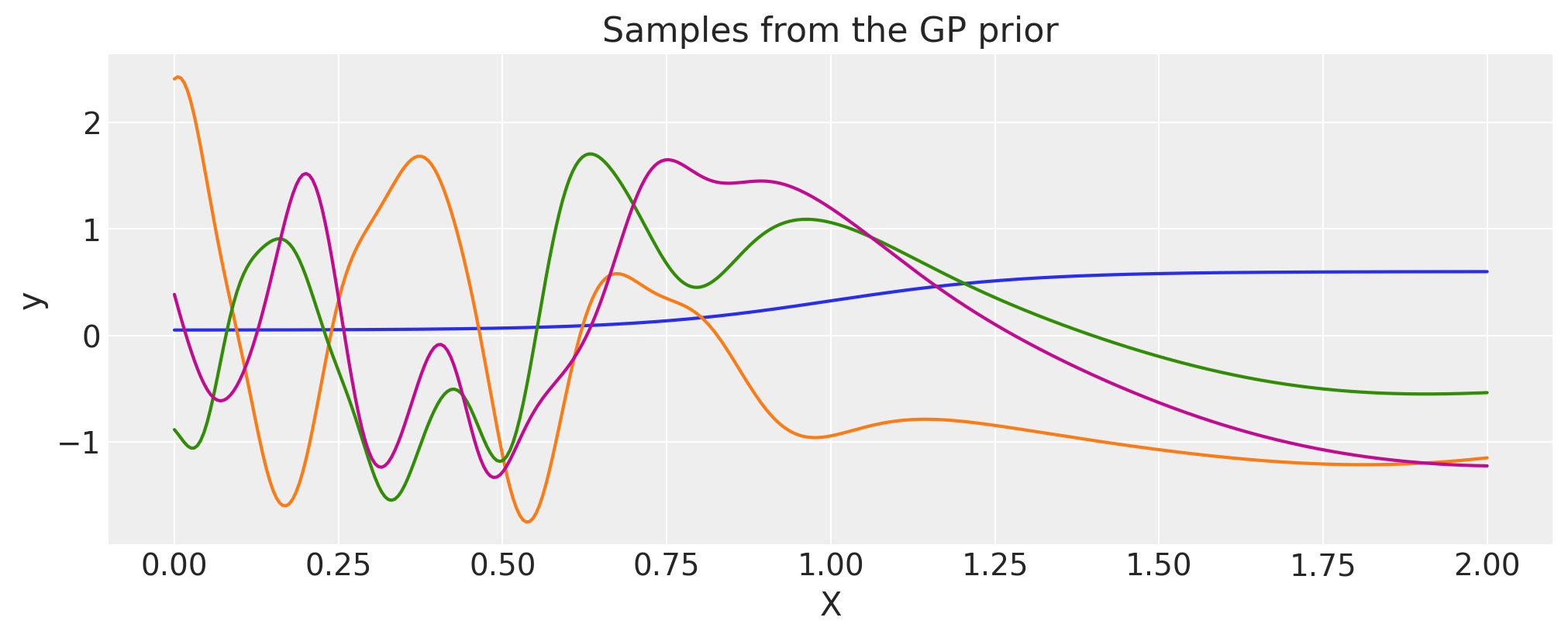
../../../_images/8b00c9a743465c012b12bb8a9b1cc7078f7d31fd77b5af2752fcc4226c3910ba.png

缩放协方差#

可以通过将某个基本核函数乘以一个非负函数 \(\phi(x)\) 来构造一个新的核函数或协方差函数。

\[ k_{\mathrm{scaled}}(x, x') = \phi(x) k_{\mathrm{base}}(x, x') \phi(x') \,. \]

这对于指定协方差函数在其定义域内振幅变化的情况非常有用。

def logistic(x, a, x0, c, d):
    # a is the slope, x0 is the location
    return d * pm.math.invlogit(a * (x - x0)) + c


a = 2.0
x0 = 5.0
c = 0.1
d = 2.0

cov_base = pm.gp.cov.ExpQuad(1, 0.2)
cov = pm.gp.cov.ScaledCov(1, scaling_func=logistic, args=(a, x0, c, d), cov_func=cov_base)
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-5)

X = np.linspace(0, 10, 400)[:, None]
lfunc = logistic(X.flatten(), a, b, c, d).eval()

plt.plot(X, lfunc)
plt.xlabel("X")
plt.ylabel(r"$\phi(x)$")
plt.title("The scaling function")

K = cov(X).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
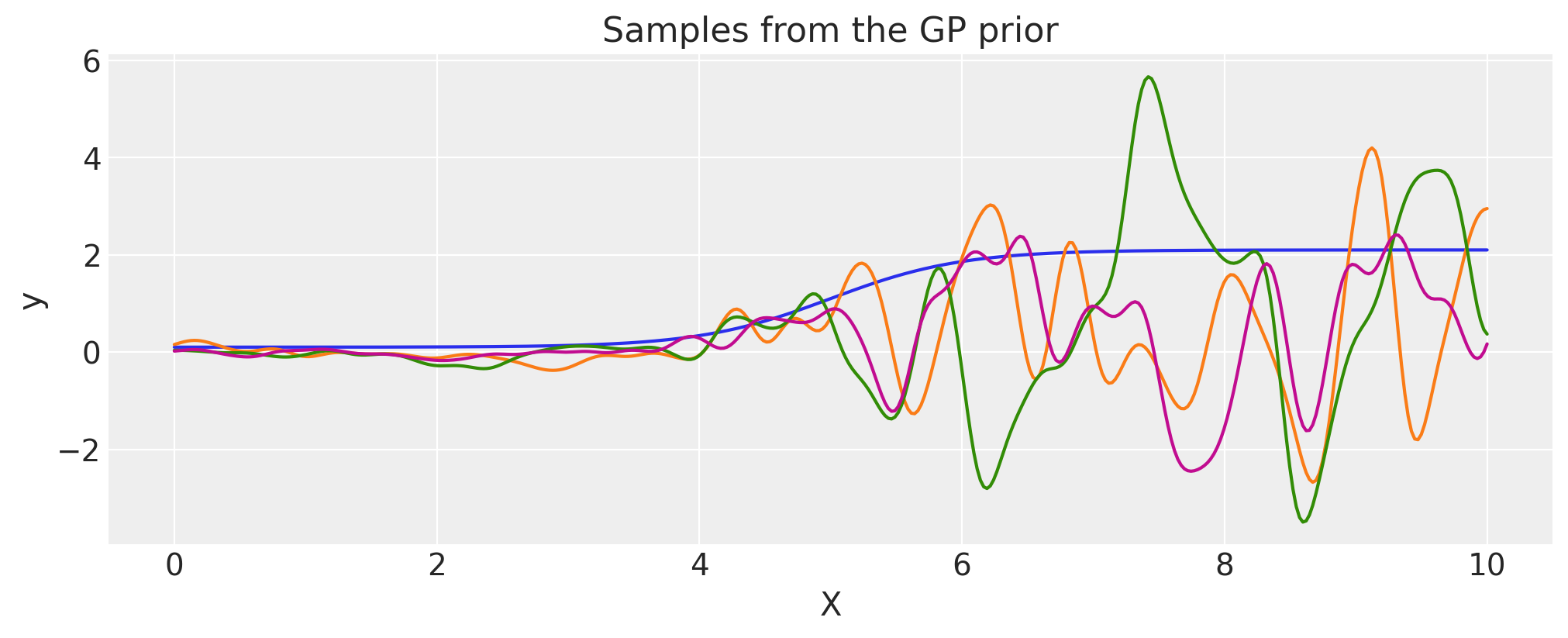
../../../_images/dd3acd30c7c9867a0a04ebcac57618386506ec3b892b3ef10a90632aaa2b4ff4.png

使用ScaledCov构建一个变化点核#

The ScaledCov 核函数可以用来创建 Changepoint 协方差。这种协方差模型描述了一个过程，该过程逐渐从一种行为类型过渡到另一种行为类型。

变化点核由以下公式给出

\[ k(x, x') = \phi(x)k_{1}(x, x')\phi(x) + (1 - \phi(x))k_{2}(x, x')(1 - \phi(x')) \]

其中 \(\phi(x)\) 是逻辑函数。

def logistic(x, a, x0):
    # a is the slope, x0 is the location
    return pm.math.invlogit(a * (x - x0))


a = 2.0
x0 = 5.0

cov1 = pm.gp.cov.ScaledCov(
    1, scaling_func=logistic, args=(-a, x0), cov_func=pm.gp.cov.ExpQuad(1, 0.2)
)
cov2 = pm.gp.cov.ScaledCov(
    1, scaling_func=logistic, args=(a, x0), cov_func=pm.gp.cov.Cosine(1, 0.5)
)
cov = cov1 + cov2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-5)

X = np.linspace(0, 10, 400)
plt.fill_between(
    X,
    np.zeros(400),
    logistic(X, -a, x0).eval(),
    label="ExpQuad region",
    color="slateblue",
    alpha=0.4,
)
plt.fill_between(
    X, np.zeros(400), logistic(X, a, x0).eval(), label="Cosine region", color="firebrick", alpha=0.4
)
plt.legend()
plt.xlabel("X")
plt.ylabel(r"$\phi(x)$")
plt.title("The two scaling functions")

K = cov(X[:, None]).eval()
plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/f46cf4b68216f30aa74278b3869e92133129d550799ea2631cf2edac64e0c4ef.png

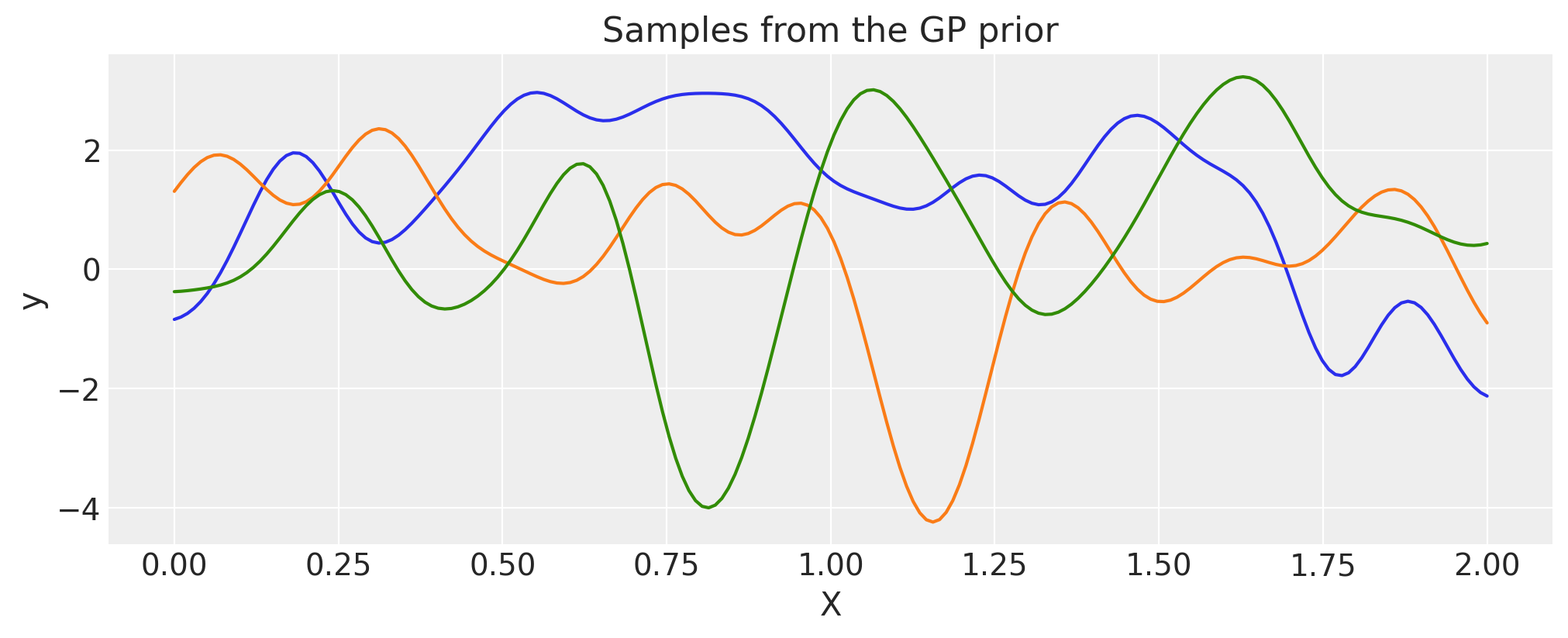
两个或多个协方差函数的组合#

您可以结合不同的协方差函数来建模复杂的数据。

特别是，您可以对任何协方差函数执行以下操作：

  • 添加其他协方差函数，其维度与第一个协方差函数相等或可广播

  • 与标量或具有相同或可广播维度的协方差函数相乘，并与第一个协方差函数结合

  • 使用标量进行指数运算。

加法#

ls_1 = 0.1
tau_1 = 2.0
ls_2 = 0.5
tau_2 = 1.0
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov_2 = tau_2 * pm.gp.cov.ExpQuad(1, ls=ls_2)

cov = cov_1 + cov_2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/c42ce6bfaf672cce11e86735fe8c738c88dba6d70703f05adc43a2d3d54dcb76.png

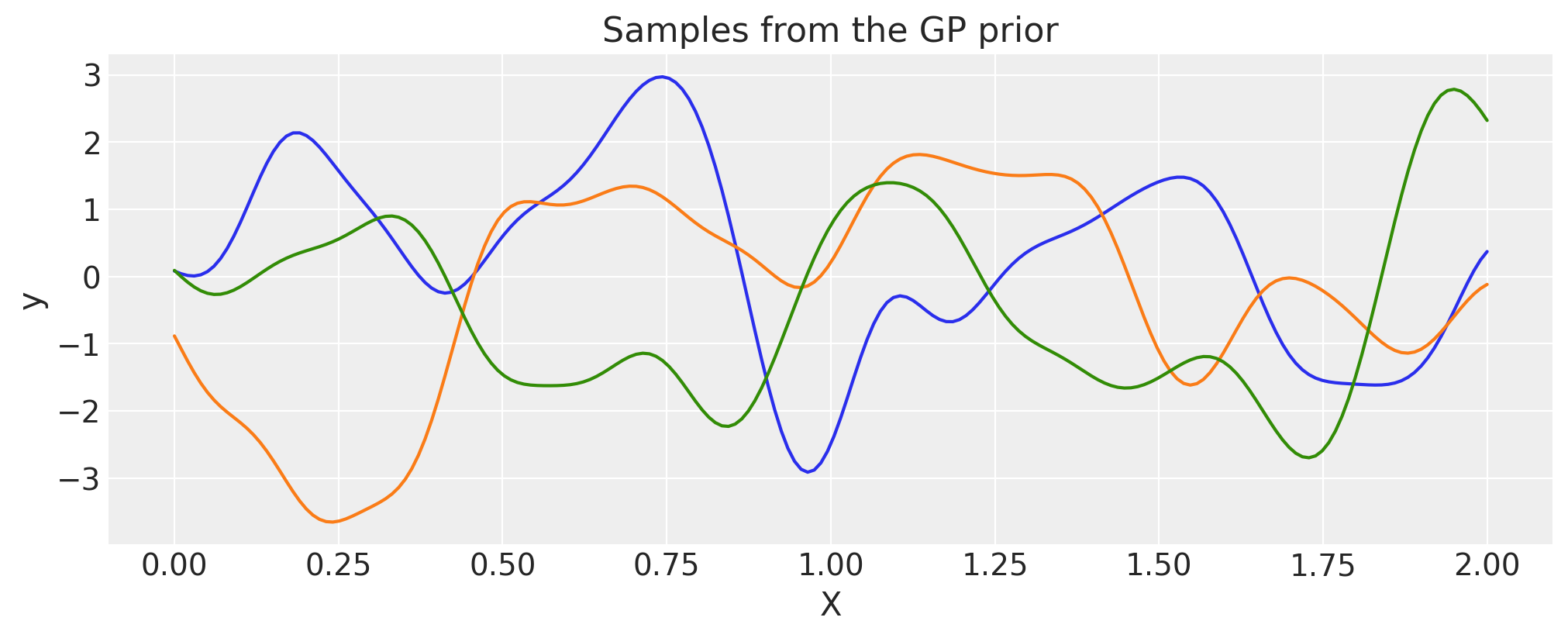
乘法#

ls_1 = 0.1
tau_1 = 2.0
ls_2 = 0.5
tau_2 = 1.0
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)
cov_2 = tau_2 * pm.gp.cov.ExpQuad(1, ls=ls_2)

cov = cov_1 * cov_2
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/14a070e3680e48e0009ae52f369aea5a8280af7b09829526b89abf2a6fce0ae0.png

指数运算#

ls_1 = 0.1
tau_1 = 2.0
power = 2
cov_1 = tau_1 * pm.gp.cov.ExpQuad(1, ls=ls_1)

cov = cov_1**power
# Add white noise to stabilise
cov += pm.gp.cov.WhiteNoise(1e-6)

X = np.linspace(0, 2, 200)[:, None]
K = cov(X).eval()

plt.plot(
    X,
    pm.draw(pm.MvNormal.dist(mu=np.zeros(len(K)), cov=K, shape=len(K)), draws=3, random_seed=rng).T,
)
plt.title("Samples from the GP prior")
plt.ylabel("y")
plt.xlabel("X");
../../../_images/6c071d02ad948c36537eee48a89de646893668dd1a7ddf9e7ee4081453fe6753.png

定义自定义协方差函数#

PyMC中的协方差函数对象需要实现__init__、diag和full方法，并且是gp.cov.Covariance的子类。diag仅返回协方差矩阵的对角线，而full返回完整的协方差矩阵。full方法有两个输入X和Xs。full(X)返回方形的协方差矩阵，而full(X, Xs)返回两组输入之间的交叉协方差。

例如，这里是 WhiteNoise 协方差函数的实现：

class WhiteNoise(pm.gp.cov.Covariance):
    def __init__(self, sigma):
        super(WhiteNoise, self).__init__(1, None)
        self.sigma = sigma

    def diag(self, X):
        return tt.alloc(tt.square(self.sigma), X.shape[0])

    def full(self, X, Xs=None):
        if Xs is None:
            return tt.diag(self.diag(X))
        else:
            return tt.alloc(0.0, X.shape[0], Xs.shape[0])

如果我们遗漏了重要的协方差或均值函数，请随时提交拉取请求！

参考资料#

[1]

卡尔·爱德华·拉斯穆森和克里斯托弗·K.I.威廉姆斯。《高斯过程在机器学习中的应用》。麻省理工学院出版社，2006年。ISBN 026218253X。网址：https://gaussianprocess.org/gpml/。

[2]

Espéran Padonou 和 O Roustant。用于在圆形域上预测的极性高斯过程。工作论文或预印本，2015年2月。URL: https://hal.archives-ouvertes.fr/hal-01119942.

作者#

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p xarray

Last updated: Fri Nov 17 2023

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.17.2

xarray: 2023.10.1

matplotlib: 3.8.1
arviz     : 0.16.1
pymc      : 5.9.2
pytensor  : 2.17.4
numpy     : 1.26.2

Watermark: 2.4.3