使用带标记的对数高斯Cox过程建模空间点模式#

介绍#

对数高斯Cox过程（LGCP）是一种点模式的概率模型，通常在空间或时间中观察到。它有两个主要组成部分。首先，在整个域\(X\)上使用指数变换的高斯过程对正实数值的潜在强度场\(\lambda(s)\)进行建模，这使得\(\lambda\)保持为正。然后，使用这个强度场来参数化一个泊松点过程，该过程表示在空间中放置点的随机机制。一些适合这种表示的现象包括一个县内癌症病例的发生率，或城市中犯罪事件的时空位置。尽管本教程仅涉及二维空间数据，但在此框架内可以同等处理空间和时间维度。

更正式地说，如果我们有一个空间 \(X\) 和 \(A\subseteq X\)，子集 \(A\) 内发生的点数 \(Y_A\) 的分布由

\[Y_A \sim Poisson\left(\int_A \lambda(s) ds\right)\]

强度场定义为

\[\log \lambda(s) \sim GP(\mu(s), K(s,s'))\]

其中 \(GP(\mu(s), K(s,s'))\) 表示具有均值函数 \(\mu(s)\) 和协方差核 \(K(s,s')\) 的高斯过程，位置为 \(s \in X\)。这是记录为任意度量空间中位置 \(s_1,...,s_n\) 的 \(n\) 个事件的点模式的最简单模型之一。结合贝叶斯分析，该模型可用于回答诸如以下感兴趣的问题：

观察到的点模式是否意味着空间强度发生了统计学上显著的变化？
具有相同统计特性的随机采样模式会是什么样子？
点事件的频率和幅度之间是否存在统计相关性？

在本笔记本中，我们将使用基于网格的近似方法来处理完整的LGCP，并使用PyMC来拟合模型并分析其后验摘要。我们还将探讨标记泊松过程的使用，这是对该模型的一种扩展，用于处理与每个数据点相关的标记的分布。

数据#

我们的观测数据涉及231个海葵，它们的大小和在法国海岸的位置已被记录。这些数据来自R中的spatstat空间建模包，该包旨在解决LGCP及其后续改进等模型。该数据的原始来源是Upton和Fingleton（1985）的教科书《Spatial data analysis by example》，有关数据的更详细描述可以在那里找到。

import warnings

from itertools import product

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm

from matplotlib import MatplotlibDeprecationWarning
from numpy.random import default_rng

warnings.filterwarnings(action="ignore", category=MatplotlibDeprecationWarning)

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

data = pd.read_csv(pm.get_data("anemones.csv"))
n = data.shape[0]

此数据集包含每个海葵的坐标和离散标记值。虽然这些标记是整数，但为了简化起见，我们将在后续步骤中将这些值建模为连续值。

data.head(3)

	x	y	marks
0	27	7	6
1	197	5	4
2	74	15	4

让我们在二维空间中看一下这些数据：

plt.scatter(data["x"], data["y"], c=data["marks"])
plt.colorbar(label="Anemone size")
plt.axis("equal");

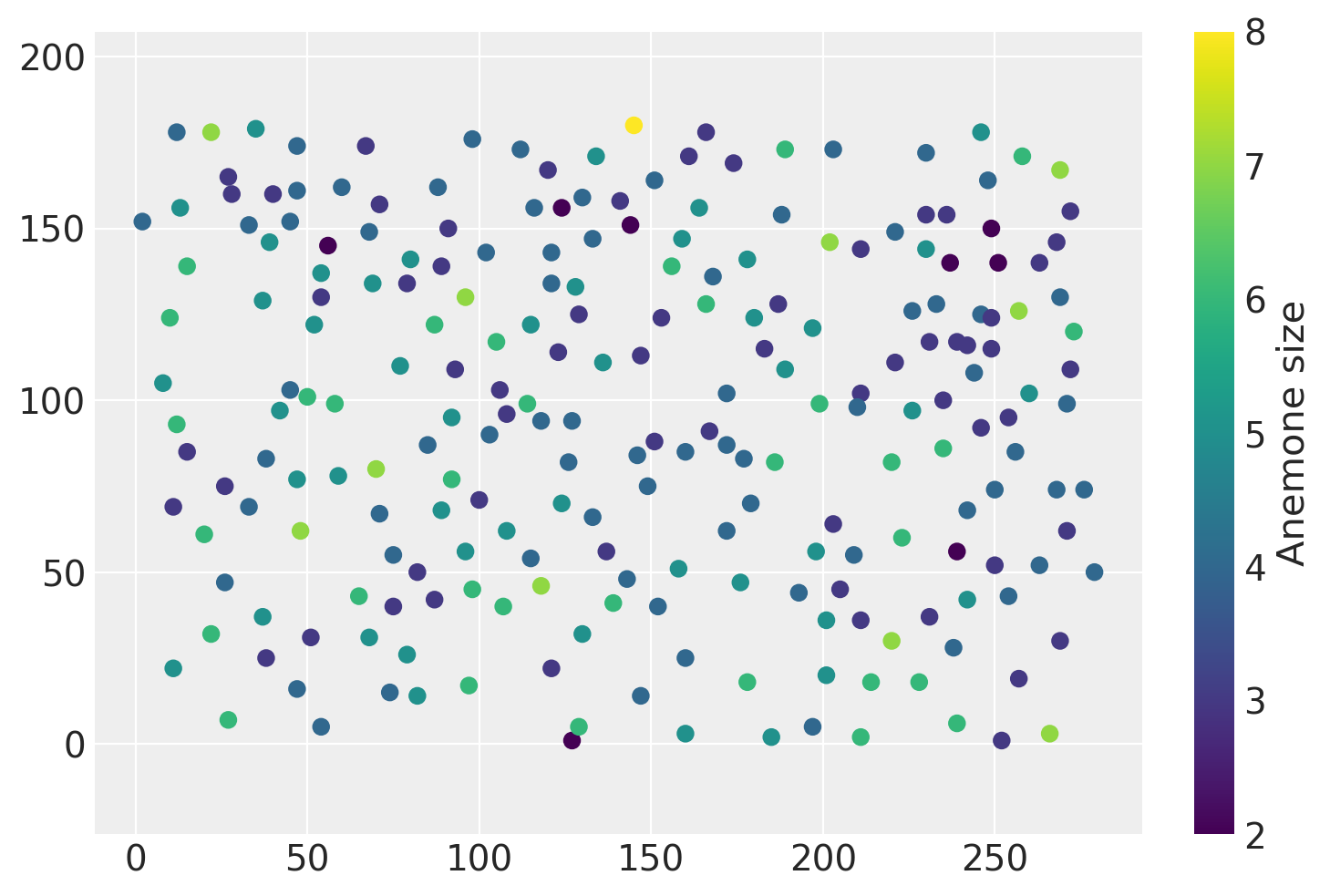
../../../_images/b6c86a8daa0f88300d9775ace3f5d5908f43487ad9d6cd5418669d807bb91e09.png

‘marks’ 列表示每个海葵的大小。如果我们同时对标记和点的空间分布进行建模，我们就是在对 标记的泊松点过程 进行建模。将基本点模式模型扩展以包含此特征是本笔记本的第二部分。

虽然有多种进行推理的方法，但最简单的方法可能是将我们的域 \(X\) 分割成许多小块 \(A_1, A_2,...,A_M\) 并将强度场固定在每个子集内为常数。然后，我们将每个 \(A_j\) 内的点数视为泊松随机变量，使得 \(Y_j \sim Poisson(\lambda_j)\)。我们还考虑 \(\log{\lambda_1}...,\log{\lambda_M}\) 变量作为从高斯过程的一次抽取。

下面的代码将域分割成网格单元，计算每个单元内的点数，并识别其质心。

xy = data[["x", "y"]].values

# Jitter the data slightly so that none of the points fall exactly
# on cell boundaries
eps = 1e-3
rng = default_rng()
xy = xy.astype("float") + rng.standard_normal(xy.shape) * eps

resolution = 20

# Rescaling the unit of area so that our parameter estimates
# are easier to read
area_per_cell = resolution**2 / 100

cells_x = int(280 / resolution)
cells_y = int(180 / resolution)

# Creating bin edges for a 2D histogram
quadrat_x = np.linspace(0, 280, cells_x + 1)
quadrat_y = np.linspace(0, 180, cells_y + 1)

# Identifying the midpoints of each grid cell
centroids = np.asarray(list(product(quadrat_x[:-1] + 10, quadrat_y[:-1] + 10)))

cell_counts, _, _ = np.histogram2d(xy[:, 0], xy[:, 1], [quadrat_x, quadrat_y])
cell_counts = cell_counts.ravel().astype(int)

将点分割到不同的单元格并计算单元格中心后，我们可以绘制如下所示的新网格化数据集。

line_kwargs = {"color": "k", "linewidth": 1, "alpha": 0.5}

plt.figure(figsize=(6, 4.5))
[plt.axhline(y, **line_kwargs) for y in quadrat_y]
[plt.axvline(x, **line_kwargs) for x in quadrat_x]
plt.scatter(data["x"], data["y"], c=data["marks"], s=6)

for i, row in enumerate(centroids):
    shifted_row = row - 2
    plt.annotate(cell_counts[i], shifted_row, alpha=0.75)

plt.title("Anemone counts per grid cell"), plt.colorbar(label="Anemone size");

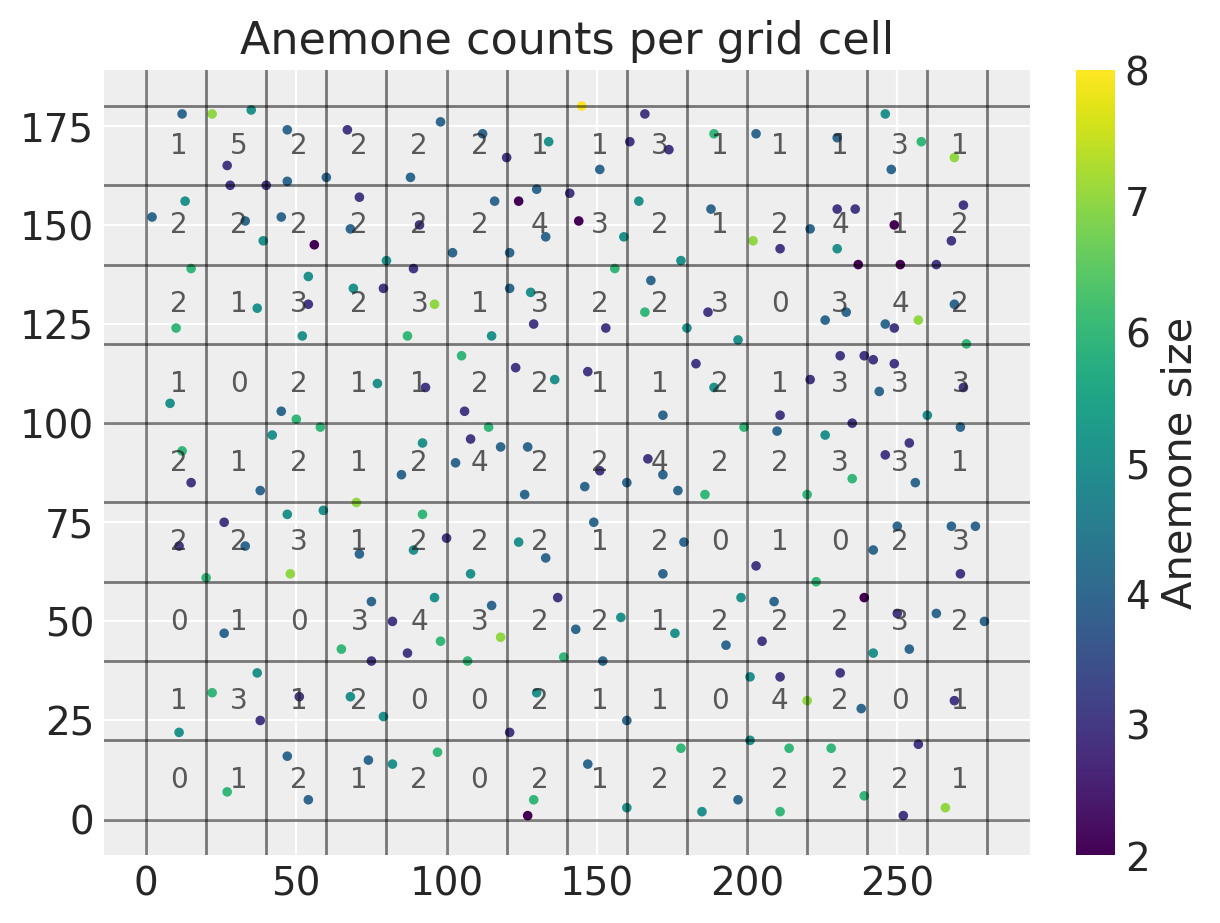
../../../_images/57dc9414e73e2abd1d9215af366d6db53039a9421292ace2c8021b6fdf4e0149.png

我们可以看到所有的计数都相当低，范围从零到五。在准备好所有数据后，我们可以继续在PyMC中编写我们的概率模型。我们将把上述每个单元格的计数\(Y_1,...Y_M\)视为泊松随机变量。

推理#

我们的第一步是为高斯过程的高级参数设置先验分布。这包括协方差函数的长度尺度 \(\rho\) 和GP的常数均值 \(\mu\)。

with pm.Model() as lgcp_model:
    mu = pm.Normal("mu", sigma=3)
    rho = pm.Uniform("rho", lower=25, upper=300)
    variance = pm.InverseGamma("variance", alpha=1, beta=1)
    cov_func = variance * pm.gp.cov.Matern52(2, ls=rho)
    mean_func = pm.gp.mean.Constant(mu)

接下来，我们通过pm.math.exp将高斯过程转换为正值过程，并使用每个细胞的面积将强度函数\(\lambda(s)\)转换为速率\(\lambda_i\)，这些速率参数化了泊松似然性，用于细胞\(i\)内的计数。

with lgcp_model:
    gp = pm.gp.Latent(mean_func=mean_func, cov_func=cov_func)

    log_intensity = gp.prior("log_intensity", X=centroids)
    intensity = pm.math.exp(log_intensity)

    rates = intensity * area_per_cell
    counts = pm.Poisson("counts", mu=rates, observed=cell_counts)

模型完全指定后，我们可以使用默认的NUTS采样器从后验分布中进行采样。我还会调整目标接受率以减少分歧的数量。

with lgcp_model:
    trace = pm.sample(1000, tune=2000, target_accept=0.95)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, rho, variance, log_intensity_rotated_]

100.00% [12000/12000 2:15:23<00:00 Sampling 4 chains, 3 divergences]

Sampling 4 chains for 2_000 tune and 1_000 draw iterations (8_000 + 4_000 draws total) took 8125 seconds.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.

解释结果#

对length_scale参数的后验推断有助于理解数据中是否存在长程相关性。我们还可以检查对数强度场的均值，但由于它是在对数尺度上，因此很难直接解释。

az.summary(trace, var_names=["mu", "rho"])

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	-0.929	0.642	-2.186	0.293	0.012	0.009	2825.0	2025.0	1.0
rho	243.612	44.685	161.203	299.971	0.658	0.470	4083.0	2785.0	1.0

我们还对在空间中大量新点处查看强度场的值感兴趣。我们可以在模型中通过包含一个新的随机变量来适应这一点，该变量用于在更密集的一组点上评估潜在的高斯过程。使用sample_posterior_predictive，我们在包含在变量intensity_new中的新数据点上生成后验预测。

x_new = np.linspace(5, 275, 20)
y_new = np.linspace(5, 175, 20)
xs, ys = np.asarray(np.meshgrid(x_new, y_new))
xy_new = np.asarray([xs.ravel(), ys.ravel()]).T

with lgcp_model:
    intensity_new = gp.conditional("log_intensity_new", Xnew=xy_new)

    spp_trace = pm.sample_posterior_predictive(
        trace, var_names=["log_intensity_new"], keep_size=True
    )

trace.extend(spp_trace)
intensity_samples = np.exp(trace.posterior_predictive["log_intensity_new"])

100.00% [4000/4000 25:30<00:00]

让我们来看几个 \(\lambda(s)\) 的实现。由于样本是在对数尺度上，我们需要对它们进行指数运算以获得我们2D泊松过程的空间强度场。在下图中，观察到的点模式被叠加显示。

fig, axes = plt.subplots(2, 3, figsize=(8, 5), constrained_layout=True)
axes = axes.ravel()

field_kwargs = {"marker": "o", "edgecolor": "None", "alpha": 0.5, "s": 80}

for i in range(6):
    field_handle = axes[i].scatter(
        xy_new[:, 0], xy_new[:, 1], c=intensity_samples.sel(chain=0, draw=i), **field_kwargs
    )

    obs_handle = axes[i].scatter(data["x"], data["y"], s=10, color="k")
    axes[i].axis("off")
    axes[i].set_title(f"Sample {i}")

plt.figlegend(
    (obs_handle, field_handle),
    ("Observed data", r"Posterior draws of $\lambda(s)$"),
    ncol=2,
    loc=(0.2, -0.01),
    fontsize=14,
    frameon=False,
);

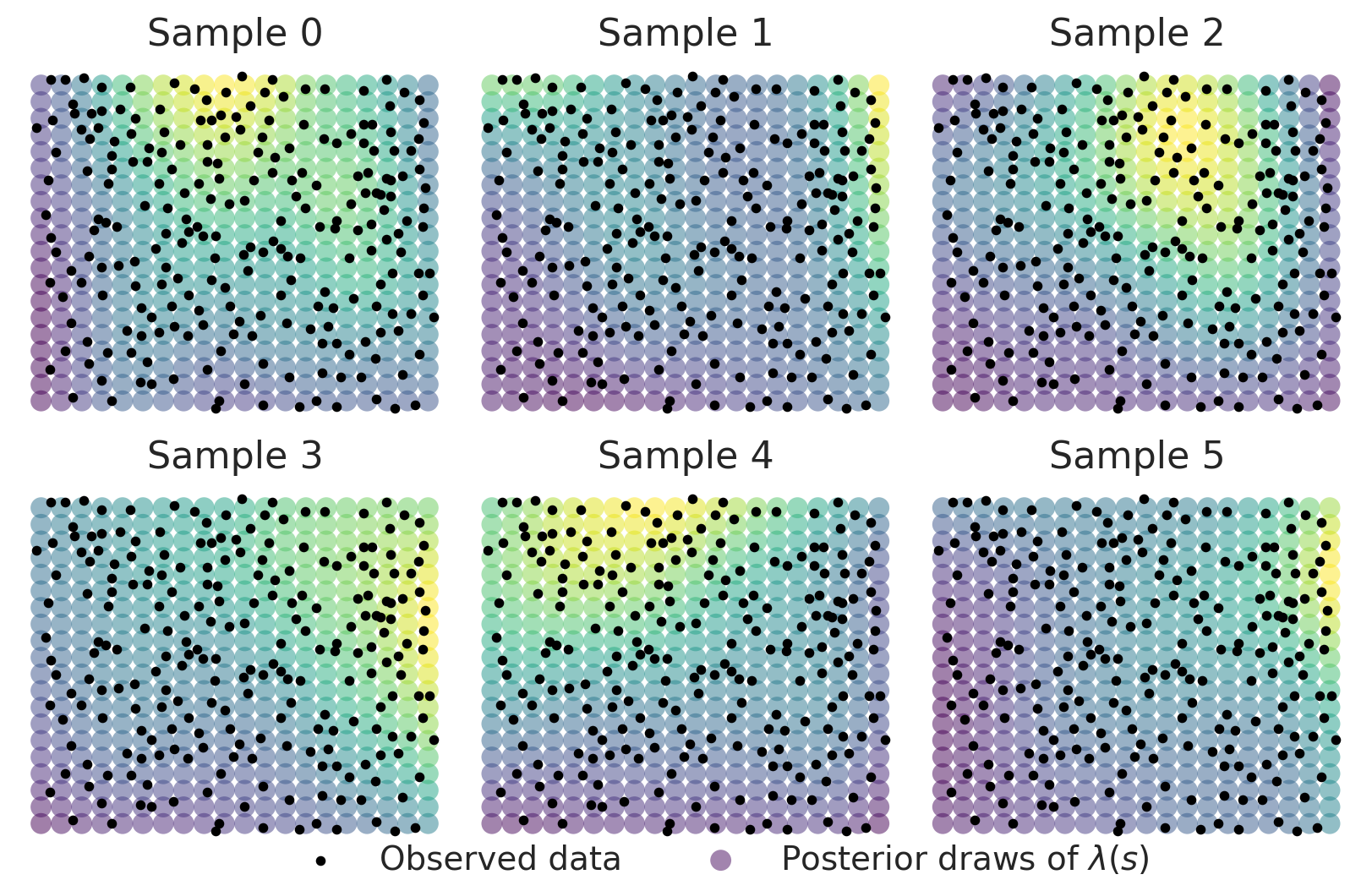
../../../_images/566460453cb0763474e685497d39949ac0884a3d505f61a543345660c21d5583.png

虽然这些表面显示出一些异质性，但我们获得了一个具有非常清晰定义空间表面的后验平均表面，右上角强度较高，左下角强度较低。

fig = plt.figure(figsize=(5, 4))

plt.scatter(
    xy_new[:, 0],
    xy_new[:, 1],
    c=intensity_samples.mean(("chain", "draw")),
    marker="o",
    alpha=0.75,
    s=100,
    edgecolor=None,
)

plt.title("$E[\\lambda(s) \\vert Y]$")
plt.colorbar(label="Posterior mean");

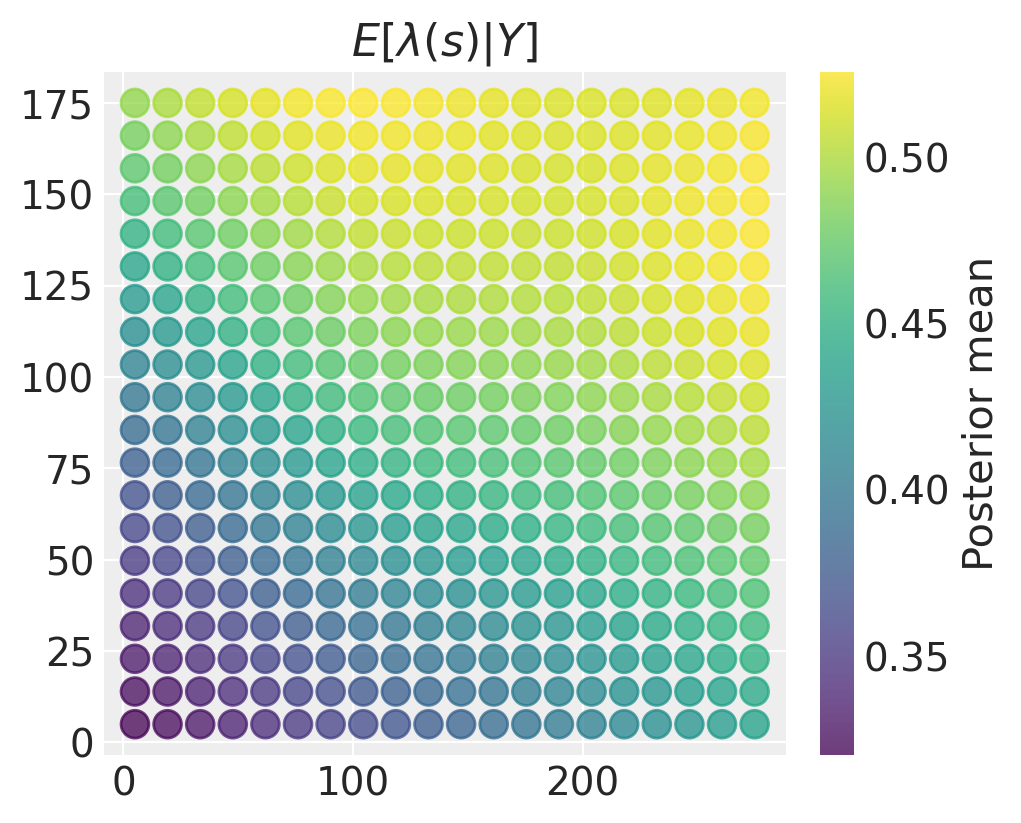
../../../_images/db0d8dbca6c81a2e63604cec58ece4fc55412132a041231f58569c6ded2be0c5.png

如果存在大量不确定性，我们估计的强度场的空间变化可能没有太大意义。在这种情况下，我们可以绘制后验方差（或标准差）的类似图：

fig = plt.figure(figsize=(5, 4))

plt.scatter(
    xy_new[:, 0],
    xy_new[:, 1],
    c=intensity_samples.var(("chain", "draw")),
    marker="o",
    alpha=0.75,
    s=100,
    edgecolor=None,
)
plt.title("$Var[\\lambda(s) \\vert Y]$"), plt.colorbar();

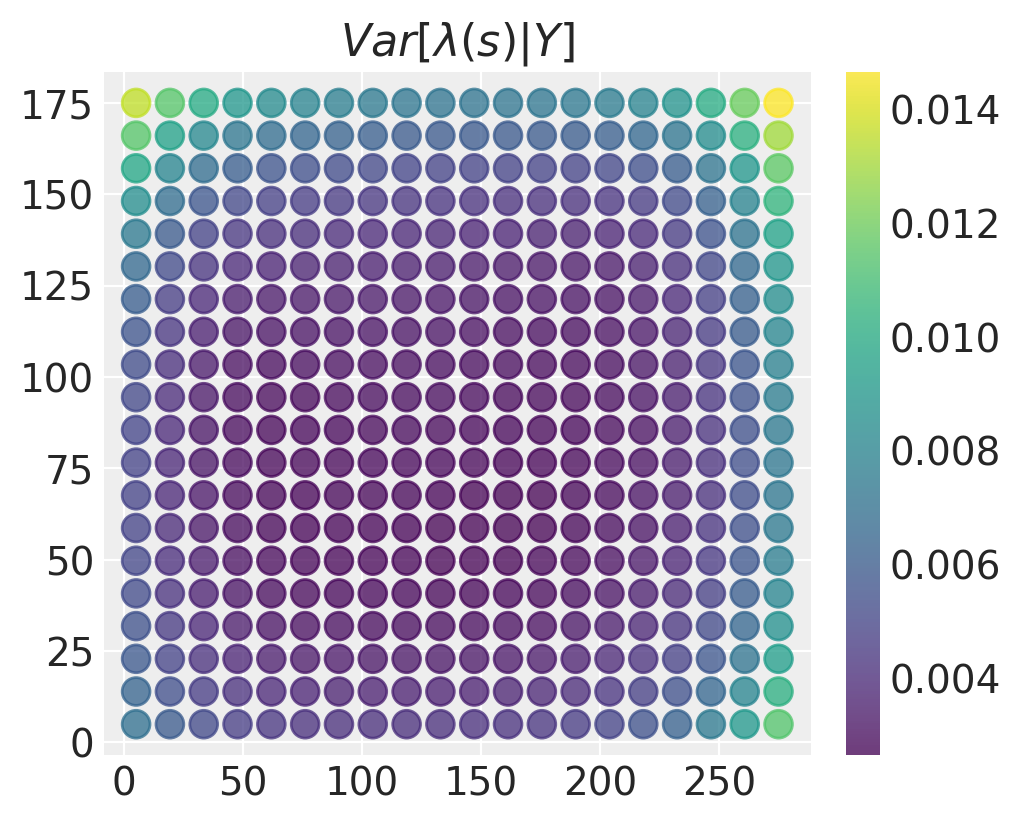
../../../_images/9845bac1c29b7414f63e6bb0bcf6b1d5d3b51362e8108f0b64d597b04fae0bb5.png

后验方差在域的中间最低，在角落和边缘最大。这是有道理的——在有更多数据的地方，我们对强度场的可能值有更准确的估计。

作者#

本笔记本由Christopher Krapu于2020年9月6日编写，并于2021年4月1日更新。
由 Chris Fonnesbeck 于 2022 年 5 月 31 日更新，以兼容 v4。

水印#

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Wed Jun 01 2022

Python implementation: CPython
Python version       : 3.9.10
IPython version      : 8.1.1

matplotlib: 3.5.1
arviz     : 0.12.0
numpy     : 1.22.2
pymc      : 4.0.0b6
pandas    : 1.4.1
sys       : 3.9.10 | packaged by conda-forge | (main, Feb  1 2022, 21:24:11) 
[GCC 9.4.0]

Watermark: 2.3.0

分类

标签

使用带标记的对数高斯Cox过程建模空间点模式#

介绍#

数据#

推理#

解释结果#

作者#

水印#