GLM: 使用自定义似然进行异常分类的稳健回归#

使用 PyMC 进行鲁棒回归，并使用 Hogg 2010 信号与噪声方法进行异常值检测。

建模概念：

  • 该模型使用自定义似然函数作为两种似然函数的混合，一种用于主要数据生成函数（我们关心的线性模型），另一种用于异常值。

  • 该模型不进行边缘化处理，因此为我们提供了每个数据点的异常程度分类

  • 数据集很小，并且硬编码在这个Notebook中。它在x和y中都包含错误，但我们这里只处理y中的错误。

补充方法：

  • 这是对示例中所示的学生-T稳健回归的补充方法 generalized_linear_models/GLM-robust，并且该方法也进行了比较

  • 另请参阅Dan FM在快速推特对话后发布的gist - 他的“Hogg改进”模型使用了相同的模型结构，并巧妙地对异常值类别进行了边缘化处理，但在采样过程中也通过pm.Deterministic对其进行了观察 - 这真的很棒

  • 似然评估本质上是对“数据分析方法：拟合模型到数据”中的公式17的复制 - Hogg 等人 [2010]

  • 该模型特别改编自Jake Vanderplas和Brigitta Sipocz在AstroML书籍中的实现 [Željko Ivezić 等, 2014, Vanderplas 等, 2012]

设置#

安装说明#

有关依赖项的完整详细信息以及笔记本编写环境的详细信息，请参阅原始项目的README。有关执行此笔记本的环境的摘要，请参阅“水印”部分。

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

导入#

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns

from matplotlib.lines import Line2D
from scipy import stats

az.style.use("arviz-darkgrid")

加载数据#

我们将使用Hogg 2010数据，该数据可在 https://github.com/astroML/astroML/blob/master/astroML/datasets/hogg2010test.py 获取

这是一个非常小的数据集，因此为了方便起见，它在下面被硬编码

# cut & pasted directly from the fetch_hogg2010test() function
# identical to the original dataset as hardcoded in the Hogg 2010 paper

dfhogg = pd.DataFrame(
    np.array(
        [
            [1, 201, 592, 61, 9, -0.84],
            [2, 244, 401, 25, 4, 0.31],
            [3, 47, 583, 38, 11, 0.64],
            [4, 287, 402, 15, 7, -0.27],
            [5, 203, 495, 21, 5, -0.33],
            [6, 58, 173, 15, 9, 0.67],
            [7, 210, 479, 27, 4, -0.02],
            [8, 202, 504, 14, 4, -0.05],
            [9, 198, 510, 30, 11, -0.84],
            [10, 158, 416, 16, 7, -0.69],
            [11, 165, 393, 14, 5, 0.30],
            [12, 201, 442, 25, 5, -0.46],
            [13, 157, 317, 52, 5, -0.03],
            [14, 131, 311, 16, 6, 0.50],
            [15, 166, 400, 34, 6, 0.73],
            [16, 160, 337, 31, 5, -0.52],
            [17, 186, 423, 42, 9, 0.90],
            [18, 125, 334, 26, 8, 0.40],
            [19, 218, 533, 16, 6, -0.78],
            [20, 146, 344, 22, 5, -0.56],
        ]
    ),
    columns=["id", "x", "y", "sigma_y", "sigma_x", "rho_xy"],
)

dfhogg["id"] = dfhogg["id"].apply(lambda x: "p{}".format(int(x)))
dfhogg.set_index("id", inplace=True)
dfhogg.head()
x y sigma_y sigma_x rho_xy
id
p1 201.0 592.0 61.0 9.0 -0.84
p2 244.0 401.0 25.0 4.0 0.31
p3 47.0 583.0 38.0 11.0 0.64
p4 287.0 402.0 15.0 7.0 -0.27
p5 203.0 495.0 21.0 5.0 -0.33

1. 基本EDA#

探索性数据分析

注意：

  • 这是非常基础的，因此我们可以快速进入 pymc3 部分

  • 数据集在x和y中都包含错误，但我们将在这里仅处理y中的错误。

  • 参见 Hogg 等人 [2010] 了解更多详情

with plt.rc_context({"figure.constrained_layout.use": False}):
    gd = sns.jointplot(
        x="x",
        y="y",
        data=dfhogg,
        kind="scatter",
        height=6,
        marginal_kws={"bins": 12, "kde": True, "kde_kws": {"cut": 1}},
        joint_kws={"edgecolor": "w", "linewidth": 1.2, "s": 80},
    )

_ = gd.ax_joint.errorbar(
    "x", "y", "sigma_y", "sigma_x", fmt="none", ecolor="#4878d0", data=dfhogg, zorder=10
)

for idx, r in dfhogg.iterrows():
    _ = gd.ax_joint.annotate(
        text=idx,
        xy=(r["x"], r["y"]),
        xycoords="data",
        xytext=(10, 10),
        textcoords="offset points",
        color="#999999",
        zorder=1,
    )


_ = gd.fig.suptitle(
    (
        "Original datapoints in Hogg 2010 dataset\n"
        + "showing marginal distributions and errors sigma_x, sigma_y"
    ),
    y=1.05,
);
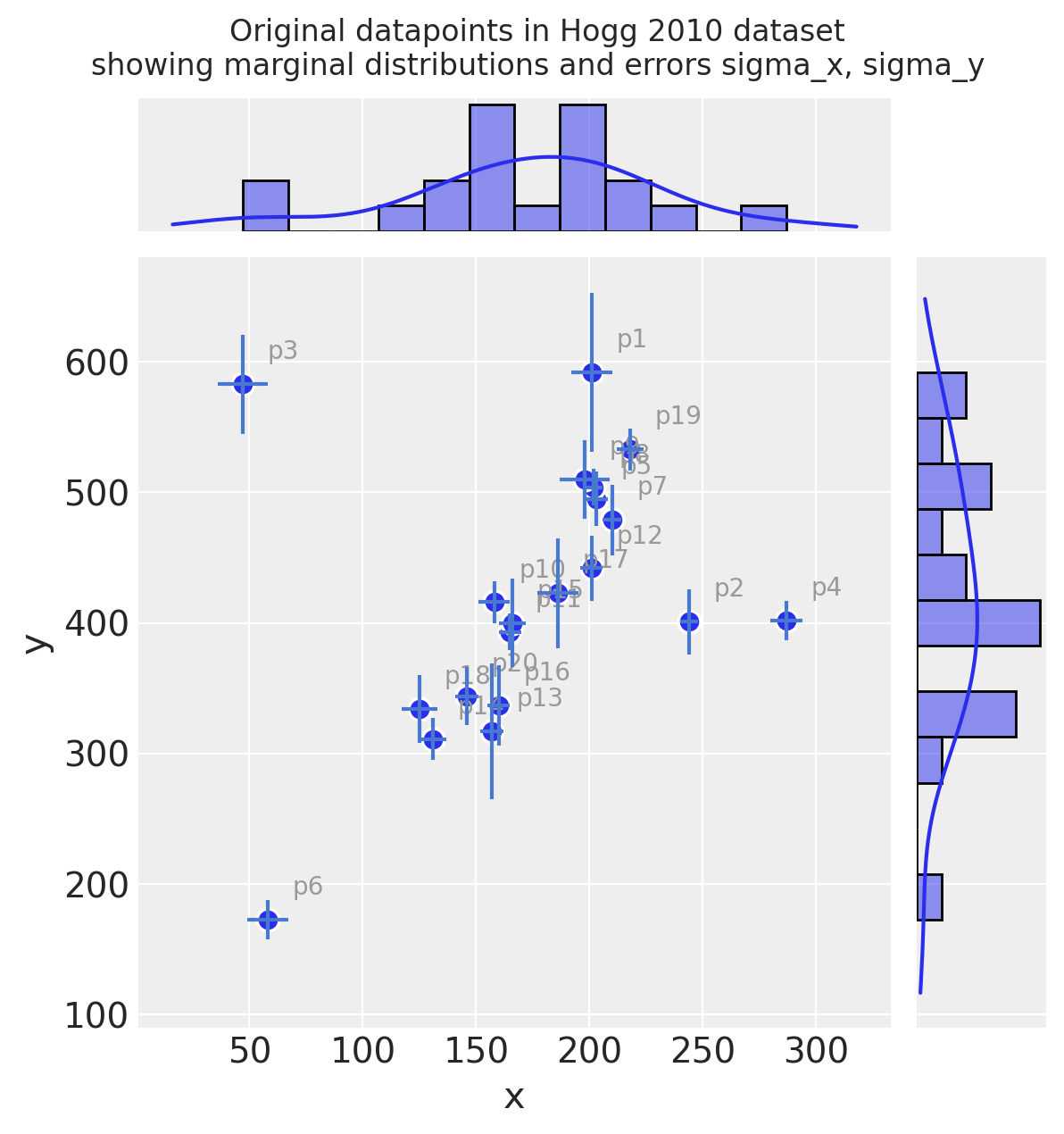
../../../_images/2f5bb1629ac3be1ecc2b35fc544b64a20ee1b7aa236ca42498440805f6ce8fc3.png

观察：

  • 即使仅凭肉眼判断，你也可以看到这些观测值大多落在/围绕在一条具有正斜率的直线上

  • 看起来有几个数据点可能是这条线的异常值

  • 测量误差（独立于x和y）在各个观测值之间有所不同

2. 基本特征工程#

2.1 转换和标准化数据集#

标准化线性模型的输入值是一种常见做法，因为这会导致系数处于相同的范围内，并且更直接地可比较。例如，这一点在Gelman [2008]中有所提及。

因此，根据Gelman的论文，我们将在这里除以2个标准差

  • 由于这个模型非常简单，我们直接进行标准化，而不是使用例如 scikit-learn 的 FunctionTransformer

  • 暂时忽略 rho_xy

关于缩放输出特征 y 和测量误差 sigma_y 的附加说明：

  • 这是不寻常的 - 通常你不会缩放一个输出特征

  • 然而，在Hogg模型中，我们拟合了一个自定义的两部分似然函数，该函数通过允许异常值拟合到它们自己的正态分布来鼓励全局最小化的对数损失。这个异常值分布是使用一个标准差指定的，该标准差被声明为从sigma_y偏移的sigma_y_out。

  • 这个偏移值的效果是要求 sigma_y 以与 y 的标准差相同的尺度重新表述

标准化（均值中心化并除以2倍标准差）：

dfhoggs = (dfhogg[["x", "y"]] - dfhogg[["x", "y"]].mean(0)) / (2 * dfhogg[["x", "y"]].std(0))
dfhoggs["sigma_x"] = dfhogg["sigma_x"] / (2 * dfhogg["x"].std())
dfhoggs["sigma_y"] = dfhogg["sigma_y"] / (2 * dfhogg["y"].std())

with plt.rc_context({"figure.constrained_layout.use": False}):
    gd = sns.jointplot(
        x="x",
        y="y",
        data=dfhoggs,
        kind="scatter",
        height=6,
        marginal_kws={"bins": 12, "kde": True, "kde_kws": {"cut": 1}},
        joint_kws={"edgecolor": "w", "linewidth": 1, "s": 80},
    )
gd.ax_joint.errorbar("x", "y", "sigma_y", "sigma_x", fmt="none", ecolor="#4878d0", data=dfhoggs)
gd.fig.suptitle(
    (
        "Quick view to confirm action of\n"
        + "standardizing datapoints in Hogg 2010 dataset\n"
        + "showing marginal distributions and errors sigma_x, sigma_y"
    ),
    y=1.08,
);
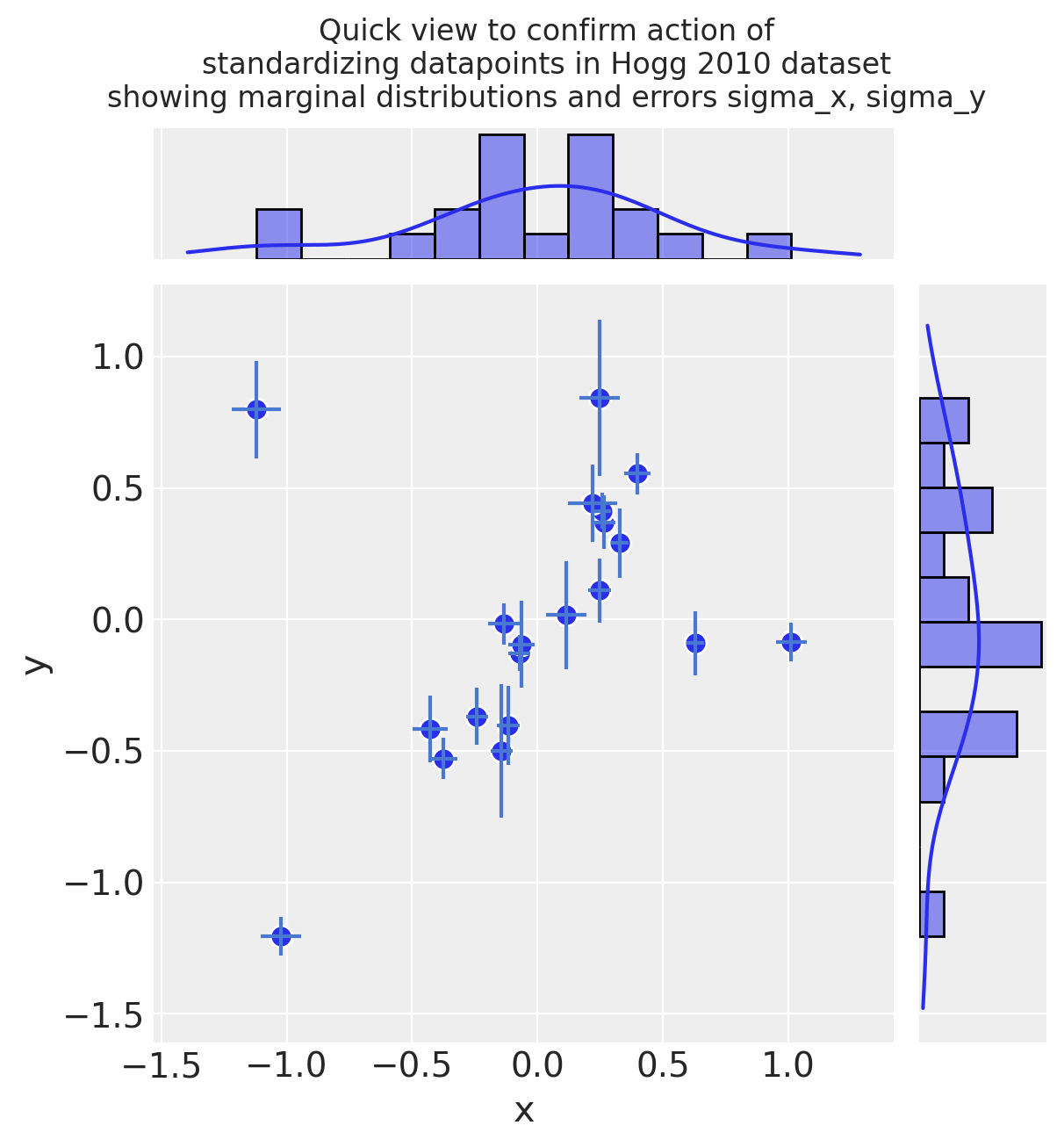
../../../_images/cb8f1229e30ef3c1a7625d6d0acabd0cbf98cd34daa201ca28b23a3f35fec33d.png

3. 无异常值校正的简单线性模型#

3.1 指定模型#

在我们进一步深入之前，我想演示一个使用正态似然函数的简单线性模型的拟合。先验分布也是正态分布的，因此这表现得像带有岭回归（L2范数）的普通最小二乘法。

注意：数据集还包含sigma_x和rho_xy，但在本次练习中，我们选择仅使用sigma_y

\[\hat{y} \sim \mathcal{N}(\beta^{T} \vec{x}_{i}, \sigma_{i})\]

其中：

  • \(\beta\) = \(\{1, \beta_{j \in X_{j}}\}\) <— 线性系数在 \(X_{j}\) 中，在这种情况下 1 + x

  • \(\sigma\) = 误差项 <— 在这种情况下，我们将其设置为未合并的 \(\sigma_{i}\)：每个数据点的测量误差 sigma_y

coords = {"coefs": ["intercept", "slope"], "datapoint_id": dfhoggs.index}
with pm.Model(coords=coords) as mdl_ols:
    # Define weakly informative Normal priors to give Ridge regression
    beta = pm.Normal("beta", mu=0, sigma=10, dims="coefs")

    # Define linear model
    y_est = beta[0] + beta[1] * dfhoggs["x"]

    # Define Normal likelihood
    pm.Normal("y", mu=y_est, sigma=dfhoggs["sigma_y"], observed=dfhoggs["y"], dims="datapoint_id")

pm.model_to_graphviz(mdl_ols)
../../../_images/5435a742fd4cdea7455782b3bd158803caad25eb5f7a500a7e6bc84ce1415e72.svg

3.2 拟合模型#

请注意，我们在这里故意省略了先验预测检查的步骤。

3.2.1 样本后验#

with mdl_ols:
    trc_ols = pm.sample(
        tune=5000,
        draws=500,
        chains=4,
        cores=4,
        init="advi+adapt_diag",
        n_init=50000,
    )
100.00% [22000/22000 00:01<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 5_000 tune and 500 draw iterations (20_000 + 2_000 draws total) took 1 seconds.

3.2.2 查看诊断信息#

注意：我们将在最终的比较图中展示这个OLS拟合并与数据点进行比较

轨迹图

_ = az.plot_trace(trc_ols, compact=False)
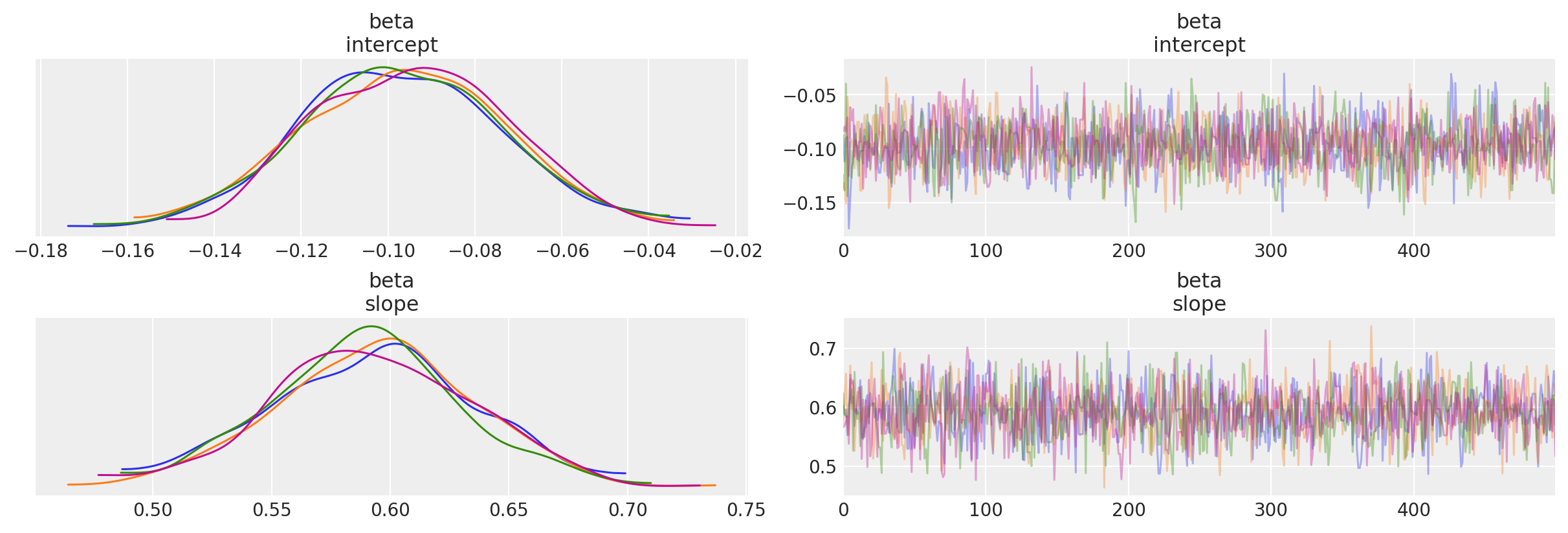
../../../_images/05af11d7b4397830355434801ea902b61f4eded5788fc6e8b5263f63c69b9845.png

绘制后验联合分布（由于模型只有2个系数，我们可以轻松地将其视为二维联合分布）

marginal_kwargs = {"kind": "kde", "rug": True, "color": "C0"}
ax = az.plot_pair(
    trc_ols,
    var_names="beta",
    marginals=True,
    kind=["scatter", "kde"],
    scatter_kwargs={"color": "C0", "alpha": 0.4},
    marginal_kwargs=marginal_kwargs,
)
fig = ax[0, 0].get_figure()
fig.suptitle("Posterior joint distribution (mdl_ols)", y=1.02);
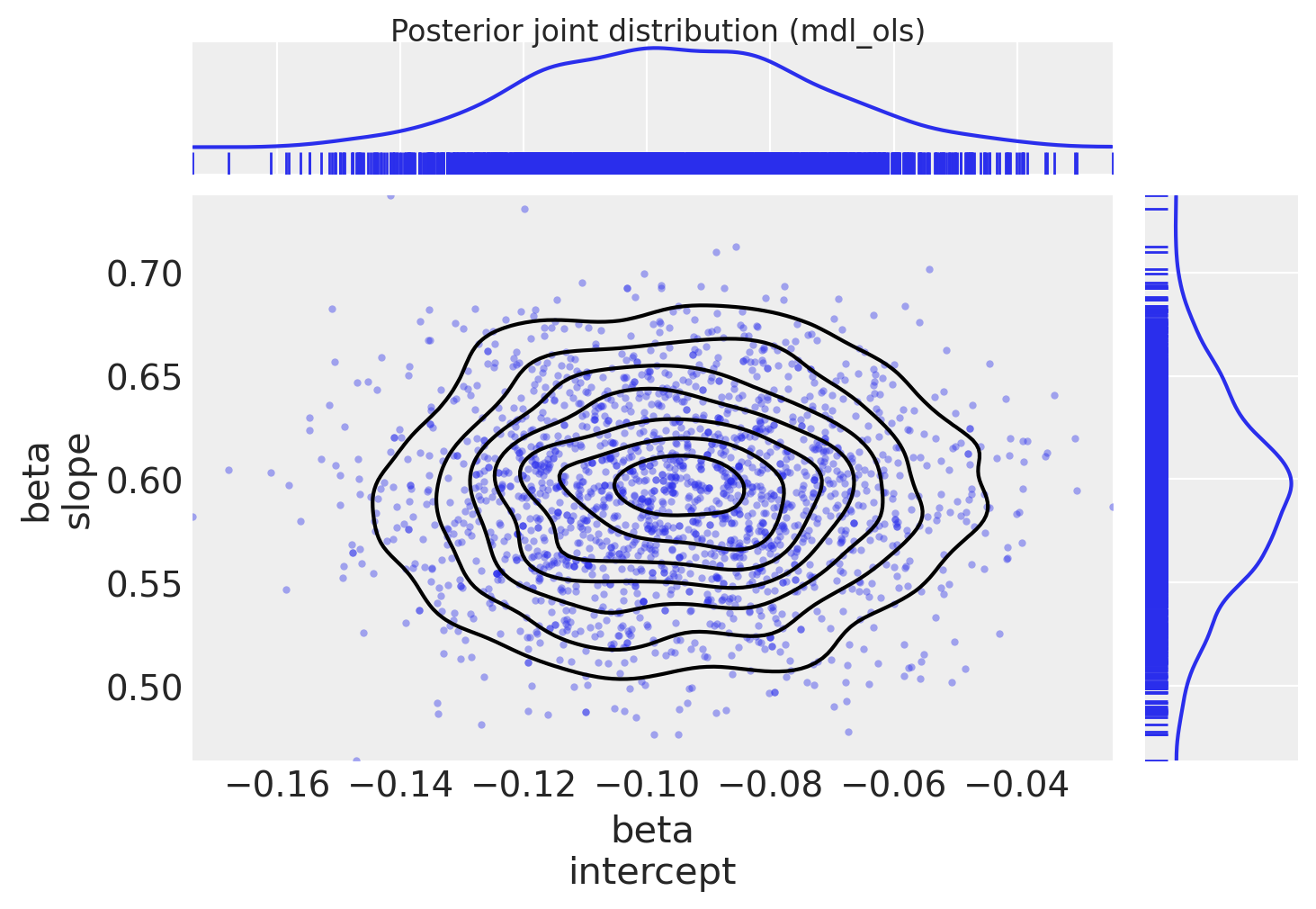
../../../_images/9e30a9295de79f14195c23eef3df8b920c3ff6f79155b9c34a1a2f9842538963.png

4. 具有稳健学生-T似然的简单线性模型#

我添加了这个简短的部分，以便直接比较在Thomas Wiecki的笔记本中示例的基于Student-T的方法，该笔记本位于PyMC3文档中

我们使用具有更厚尾部的学生T分布来代替使用正态分布作为似然函数。理论上，这使得异常值在似然估计中的影响更小。该方法不会产生内点/异常点标志（它对这种分类进行了边缘化处理），但它比下面的信号与噪声模型更简单、运行速度更快，因此进行比较似乎是值得的。

4.1 指定模型#

在这个修改中，我们允许似然函数对异常值更加鲁棒（具有更肥的尾部）

\[\hat{y} \sim \text{StudentT}(\beta^{T} \vec{x}_{i}, \sigma_{i}, \nu)\]

其中：

  • \(\beta\) = \(\{1, \beta_{j \in X_{j}}\}\) <— 线性系数在 \(X_{j}\) 中，在这种情况下 1 + x

  • \(\sigma\) = 误差项 <— 在这种情况下，我们将其设置为未合并的 \(\sigma_{i}\)：每个数据点的测量误差 sigma_y

  • \(\nu\) = 自由度 <— 允许具有较厚尾部的pdf，从而减少异常数据点的影响

注意：该数据集还包含sigma_x和rho_xy，但在本次练习中，我选择仅使用sigma_y

with pm.Model(coords=coords) as mdl_studentt:
    # define weakly informative Normal priors to give Ridge regression
    beta = pm.Normal("beta", mu=0, sigma=10, dims="coefs")

    # define linear model
    y_est = beta[0] + beta[1] * dfhoggs["x"]

    # define prior for StudentT degrees of freedom
    # InverseGamma has nice properties:
    # it's continuous and has support x ∈ (0, inf)
    nu = pm.InverseGamma("nu", alpha=1, beta=1)

    # define Student T likelihood
    pm.StudentT(
        "y", mu=y_est, sigma=dfhoggs["sigma_y"], nu=nu, observed=dfhoggs["y"], dims="datapoint_id"
    )

pm.model_to_graphviz(mdl_studentt)
../../../_images/0f437cf964a1f336d40df87f76dc122047636335794c1a6db0df09b049d320db.svg

4.2 拟合模型#

4.2.1 样本后验#

with mdl_studentt:
    trc_studentt = pm.sample(
        tune=5000,
        draws=500,
        chains=4,
        cores=4,
        init="advi+adapt_diag",
        n_init=50000,
    )
100.00% [22000/22000 00:02<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 5_000 tune and 500 draw iterations (20_000 + 2_000 draws total) took 2 seconds.

4.2.2 查看诊断信息#

注意：我们将在最终的比较图中展示这个StudentT拟合并与数据点进行比较

轨迹图

_ = az.plot_trace(trc_studentt, compact=False);
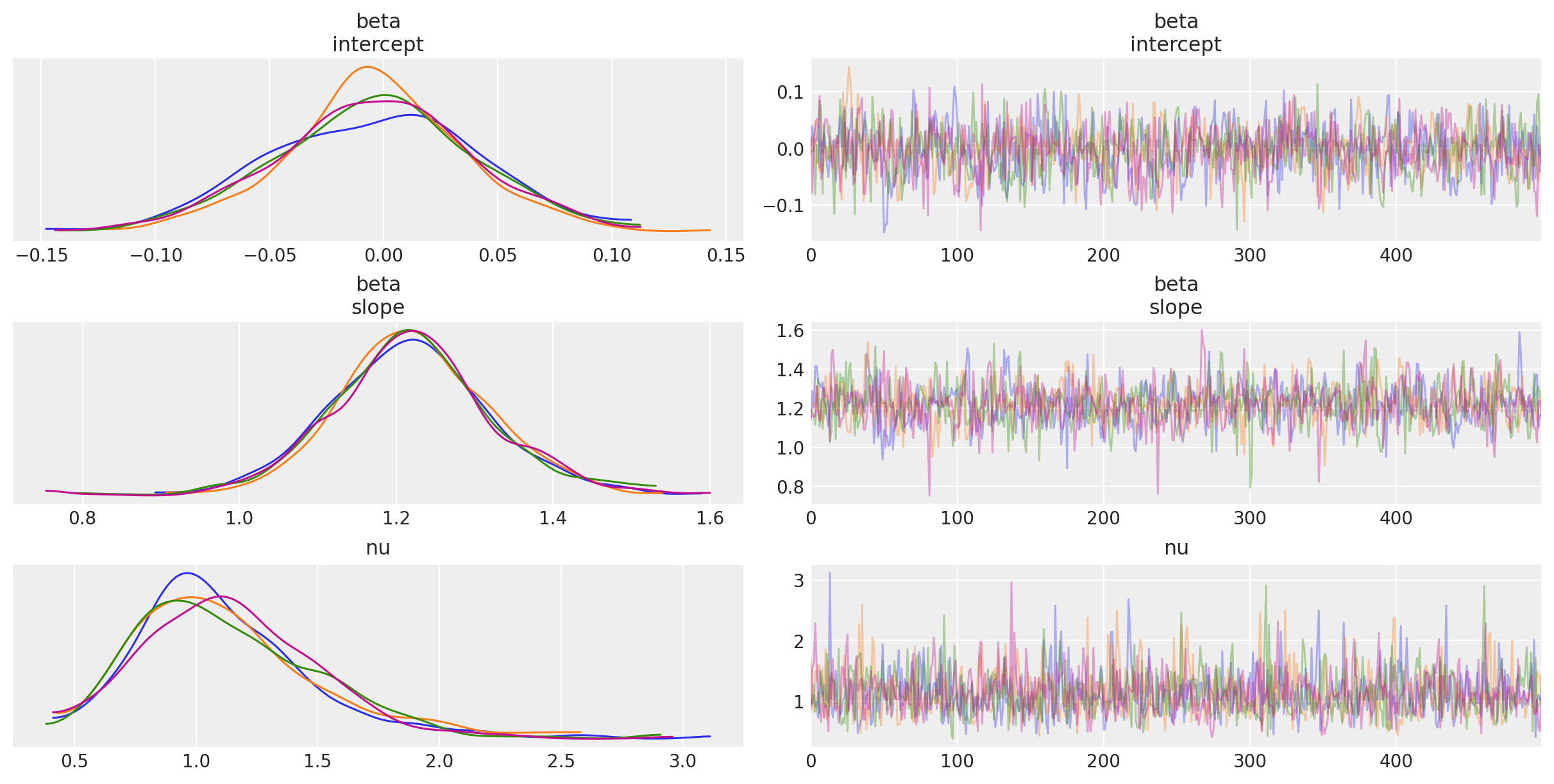
../../../_images/dc18d259681b361a990d5ff0aa6650893f4e3d409a24dae737dedc2b5d556700.png

绘制后验联合分布

marginal_kwargs["color"] = "C1"
ax = az.plot_pair(
    trc_studentt,
    var_names="beta",
    kind=["scatter", "kde"],
    divergences=True,
    marginals=True,
    marginal_kwargs=marginal_kwargs,
    scatter_kwargs={"color": "C1", "alpha": 0.4},
)
ax[0, 0].get_figure().suptitle("Posterior joint distribution (mdl_studentt)");
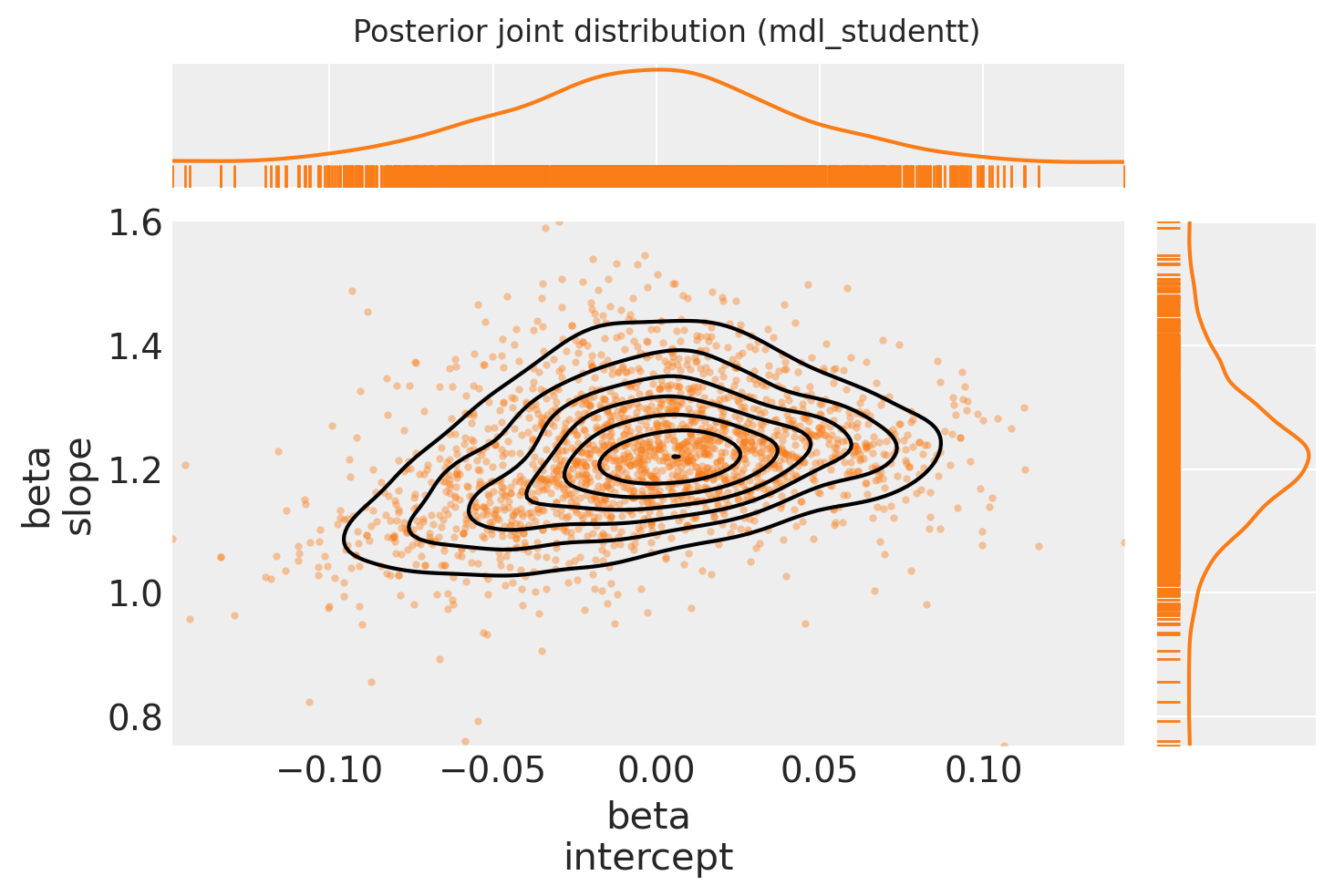
../../../_images/68551660b758ad71ce83e31eb48768a0a7d19d54229d0632be0a2e9d8f9661c5.png

4.2.3 查看从OLS到StudentT的后验联合分布的变化#

marginal_kwargs["rug"] = False
marginal_kwargs["color"] = "C0"
ax = az.plot_pair(
    trc_ols,
    var_names="beta",
    kind=["scatter", "kde"],
    divergences=True,
    figsize=[12, 12],
    marginals=True,
    marginal_kwargs=marginal_kwargs,
    scatter_kwargs={"color": "C0", "alpha": 0.4},
    kde_kwargs={"contour_kwargs": {"colors": "C0"}},
)

marginal_kwargs["color"] = "C1"
az.plot_pair(
    trc_studentt,
    var_names="beta",
    kind=["scatter", "kde"],
    divergences=True,
    marginals=True,
    marginal_kwargs=marginal_kwargs,
    scatter_kwargs={"color": "C1", "alpha": 0.4},
    kde_kwargs={"contour_kwargs": {"colors": "C1"}},
    ax=ax,
)

ax[0, 0].get_figure().suptitle(
    "Posterior joint distributions\n(showing general movement from OLS to StudentT)"
);
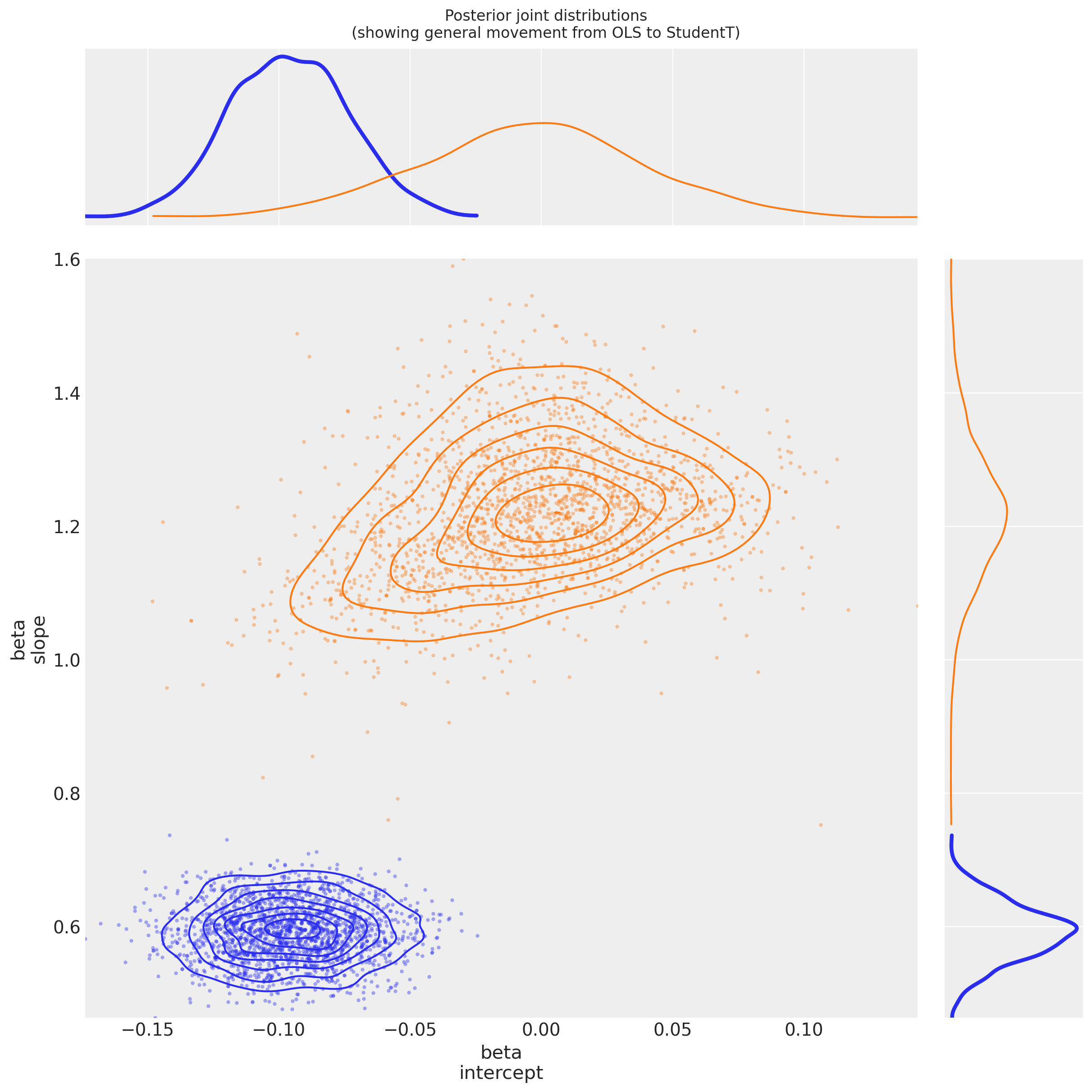
../../../_images/a15b55b859d0d8cccf03ebd3c46026c1b9a4e7eab52e911b2080e1267998d09c.png

观察：

  • 两个beta参数的方差似乎比在OLS回归中更大

  • 这是由于 \(\nu\) 似乎收敛到一个值 nu ~ 1，表明 厚尾似然比薄尾似然拟合得更好

  • 参数 beta[intercept] 已经更接近 \(0\)，这很有趣：如果理论关系 y ~ f(x) 没有偏移，那么对于这个均值中心化的数据集，截距确实应该是 \(0\)：它可能很容易被 OLS 模型中的异常值推离轨道。

  • 参数 beta[slope] 因此变得更大了：可能更接近理论函数 f(x)

5. 使用自定义似然性区分异常值的线性模型：Hogg 方法#

请阅读Hogg 2010年的论文和Jake Vanderplas的代码，以获取关于建模技术的更完整信息。

总体思路是创建一个“混合”模型，使得数据点可以由以下任一方式描述：

  1. 提出的（线性）模型（因此一个数据点是内点），或

  2. 第二个模型，为了方便我们也建议采用线性模型，但允许它具有不同的均值和方差（因此一个数据点是异常值）

5.1 指定模型#

可能性是在两个可能性的混合上进行评估的，一个是针对“内点”，一个是针对“外点”。使用伯努利分布来随机将数据点分配到内点或外点组中，我们像往常一样采样模型以推断鲁棒的模型参数和内点/外点标志：

\[ \mathcal{logL} = \sum_{i}^{i=N} log \left[ \frac{(1 - B_{i})}{\sqrt{2 \pi \sigma_{in}^{2}}} exp \left( - \frac{(x_{i} - \mu_{in})^{2}}{2\sigma_{in}^{2}} \right) \right] + \sum_{i}^{i=N} log \left[ \frac{B_{i}}{\sqrt{2 \pi (\sigma_{in}^{2} + \sigma_{out}^{2})}} exp \left( - \frac{(x_{i}- \mu_{out})^{2}}{2(\sigma_{in}^{2} + \sigma_{out}^{2})} \right) \right] \]

其中：

  • \(B_{i}\) 是伯努利分布的 \(B_{i} \in \{0_{(正常点)},1_{(异常点)}\}\)

  • \(\mu_{in} = \beta^{T} \vec{x}_{i}\) 对于内点，其中 \(\beta\) = \(\{1, \beta_{j \in X_{j}}\}\) <— 线性系数在 \(X_{j}\)，在这种情况下 1 + x

  • \(\sigma_{in}\) = 噪声项 <— 在这种情况下，我们将其设置为未池化的 \(\sigma_{i}\)：每个数据点的测量误差 sigma_y

  • \(\mu_{out}\) <— 是一个用于异常值的随机合并变量

  • \(\sigma_{out}\) = 额外的噪声项 <— 是异常值的随机未合并变量

本笔记本使用 Potential() 类与 logp 结合来创建似然并构建此模型，其中未观察到特征，这里是伯努利切换变量。

未讨论Potential的使用。其他资源值得参考，以获取有关Potential使用的详细信息：

with pm.Model(coords=coords) as mdl_hogg:
    # state input data as Theano shared vars
    tsv_x = pm.ConstantData("tsv_x", dfhoggs["x"], dims="datapoint_id")
    tsv_y = pm.ConstantData("tsv_y", dfhoggs["y"], dims="datapoint_id")
    tsv_sigma_y = pm.ConstantData("tsv_sigma_y", dfhoggs["sigma_y"], dims="datapoint_id")

    # weakly informative Normal priors (L2 ridge reg) for inliers
    beta = pm.Normal("beta", mu=0, sigma=10, dims="coefs")

    # linear model for mean for inliers
    y_est_in = beta[0] + beta[1] * tsv_x  # dims="obs_id"

    # very weakly informative mean for all outliers
    y_est_out = pm.Normal("y_est_out", mu=0, sigma=10, initval=pm.floatX(0.0))

    # very weakly informative prior for additional variance for outliers
    sigma_y_out = pm.HalfNormal("sigma_y_out", sigma=10, initval=pm.floatX(1.0))

    # create in/outlier distributions to get a logp evaluated on the observed y
    # this is not strictly a pymc3 likelihood, but behaves like one when we
    # evaluate it within a Potential (which is minimised)
    inlier_logp = pm.logp(pm.Normal.dist(mu=y_est_in, sigma=tsv_sigma_y), tsv_y)
    outlier_logp = pm.logp(pm.Normal.dist(mu=y_est_out, sigma=tsv_sigma_y + sigma_y_out), tsv_y)

    # frac_outliers only needs to span [0, .5]
    # testval for is_outlier initialised in order to create class asymmetry
    frac_outliers = pm.Uniform("frac_outliers", lower=0.0, upper=0.5)
    is_outlier = pm.Bernoulli(
        "is_outlier",
        p=frac_outliers,
        initval=(np.random.rand(tsv_x.eval().shape[0]) < 0.4) * 1,
        dims="datapoint_id",
    )

    # non-sampled Potential evaluates the Normal.dist.logp's
    potential = pm.Potential(
        "obs",
        ((1 - is_outlier) * inlier_logp).sum() + (is_outlier * outlier_logp).sum(),
    )

5.2 拟合模型#

5.2.1 样本后验#

请注意，pm.sample 方便且自动创建复合采样过程以：

  1. 使用离散采样器采样一个伯努利变量（类 is_outlier）

  2. 使用连续采样器对连续变量进行采样

进一步注意：

  • 这也意味着我们不能使用ADVI进行初始化，因此将使用jitter+adapt_diag进行初始化

  • 为了将 kwargs 传递给特定的步进器，将它们包装在一个字典中，该字典指向小写的 步进器名称，例如 nuts={'target_accept': 0.85}

with mdl_hogg:
    trc_hogg = pm.sample(
        tune=10000,
        draws=500,
        chains=4,
        cores=4,
        init="jitter+adapt_diag",
        nuts={"target_accept": 0.99},
    )
100.00% [42000/42000 00:27<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 10_000 tune and 500 draw iterations (40_000 + 2_000 draws total) took 27 seconds.
/Users/benjamv/mambaforge/envs/pymc_env/lib/python3.10/site-packages/arviz/stats/diagnostics.py:584: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)

5.2.2 查看诊断信息#

我们将展示这个模型的拟合结果，并在最终的对比图中与数据点进行比较

rvs = ["beta", "y_est_out", "sigma_y_out", "frac_outliers"]
_ = az.plot_trace(trc_hogg, var_names=rvs, compact=False);
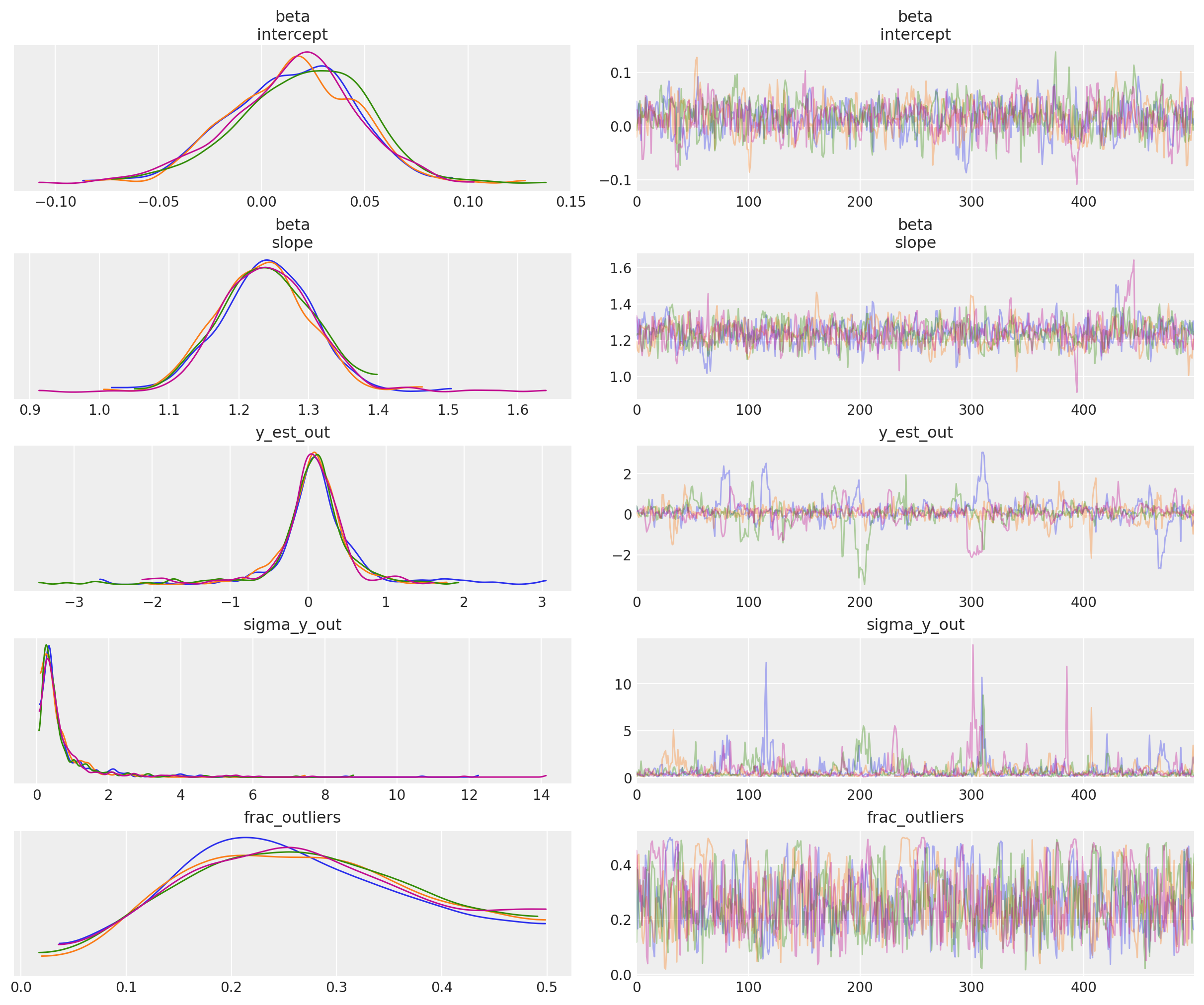
../../../_images/3036eebee456f00bc30da41df86a721c6fd27688f56caad65a5eda436f0d8c37.png

观察：

  • 在默认的 target_accept = 0.8 下，存在大量的分歧，表明这不是一个特别稳定的模型

  • 然而，在 target_accept = 0.9（并将 tune 从 5000 增加到 10000）时，轨迹表现出较少的分歧，并且看起来稍微更好。

  • 内点模型参数beta的轨迹，以及异常点模型参数y_est_out（均值）的轨迹看起来已经合理收敛

  • 异常模型参数 y_sigma_out（额外的池化方差）的轨迹偶尔会变得有点不稳定

  • 有趣的是，frac_outliers 如此分散：这是一个相当平坦的分布：表明在某些数据点上，它们的内点/离群点状态是主观的

  • 事实上，正如托马斯在他的v2.0笔记本中所指出的，因为我们明确地将潜在标签（正常/异常）建模为二元选择，采样器可能会遇到问题——将这个模型重写为边际混合模型会更好。

简单的跟踪摘要 inc rhat

az.summary(trc_hogg, var_names=rvs)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
beta[intercept] 0.016 0.031 -0.044 0.069 0.001 0.001 795.0 747.0 1.00
beta[slope] 1.239 0.068 1.124 1.365 0.003 0.002 764.0 845.0 1.01
y_est_out 0.073 0.540 -0.977 1.108 0.032 0.024 433.0 295.0 1.01
sigma_y_out 0.724 0.992 0.073 2.095 0.051 0.036 429.0 423.0 1.01
frac_outliers 0.268 0.109 0.084 0.472 0.005 0.004 554.0 656.0 1.00

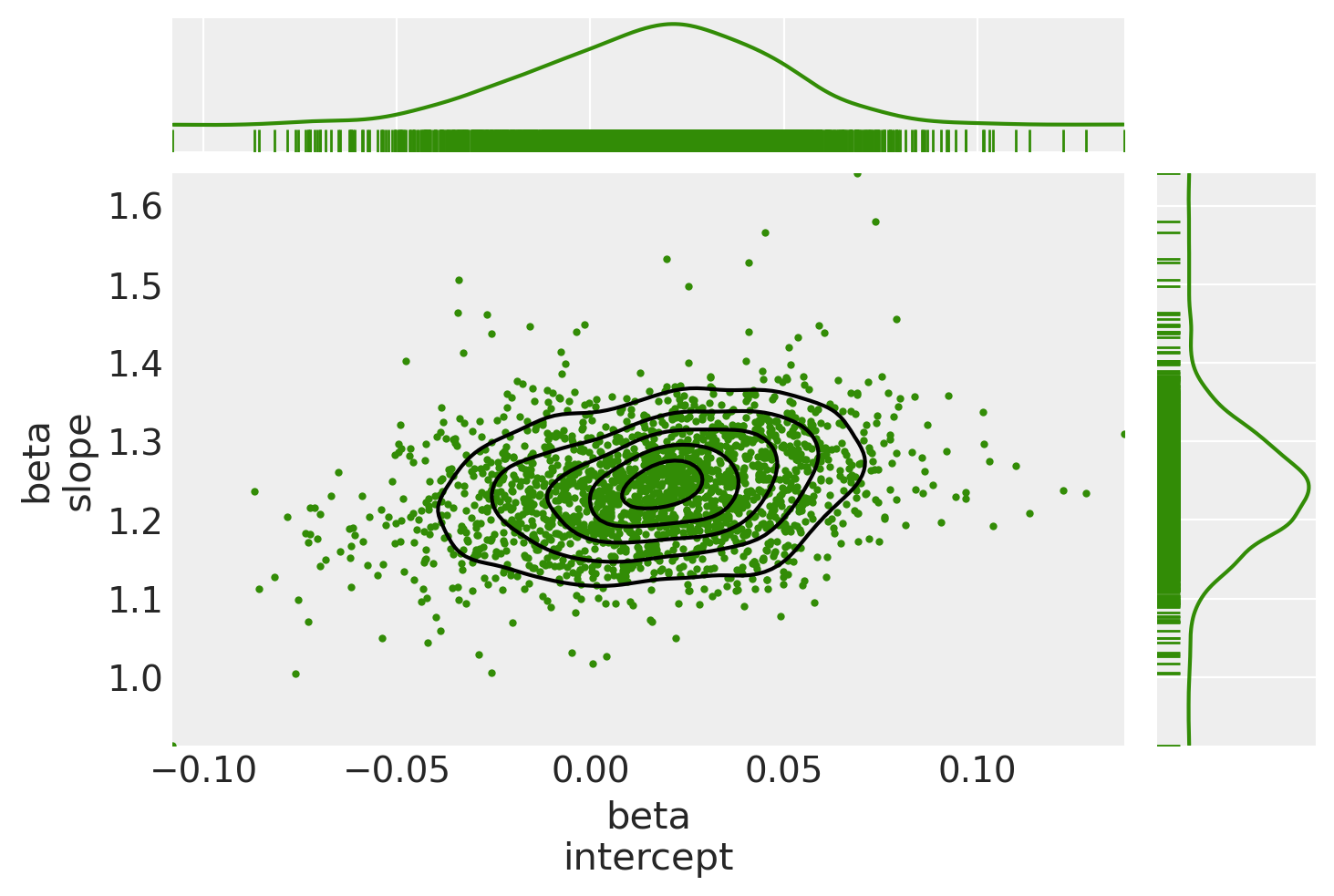
绘制后验联合分布

(在这种情况下，这是一个特别有用的诊断工具，因为我们看到轨迹中有很多分歧：可能是模型规范导致了奇怪的行为)

marginal_kwargs["color"] = "C2"
marginal_kwargs["rug"] = True
x = az.plot_pair(
    data=trc_hogg,
    var_names="beta",
    kind=["kde", "scatter"],
    divergences=True,
    marginals=True,
    marginal_kwargs=marginal_kwargs,
    scatter_kwargs={"color": "C2"},
)
ax[0, 0].get_figure().suptitle("Posterior joint distribution (mdl_hogg)");
../../../_images/04c5e7e2b5510c1d37b411e178432c6ce60baed48d325242cc4b4f781e9192cf.png

5.2.3 从OLS到StudentT再到Hogg查看后验联合分布的偏移#

kde_kwargs = {"contour_kwargs": {"colors": "C0", "zorder": 4}, "contourf_kwargs": {"alpha": 0}}
marginal_kwargs["rug"] = False
marginal_kwargs["color"] = "C0"
ax = az.plot_pair(
    trc_ols,
    var_names="beta",
    kind="kde",
    divergences=True,
    marginals=True,
    marginal_kwargs={"color": "C0"},
    kde_kwargs=kde_kwargs,
    figsize=(8, 8),
)

marginal_kwargs["color"] = "C1"
kde_kwargs["contour_kwargs"]["colors"] = "C1"
az.plot_pair(
    trc_studentt,
    var_names="beta",
    kind="kde",
    divergences=True,
    marginals=True,
    marginal_kwargs=marginal_kwargs,
    kde_kwargs=kde_kwargs,
    ax=ax,
)

marginal_kwargs["color"] = "C2"
kde_kwargs["contour_kwargs"]["colors"] = "C2"
az.plot_pair(
    data=trc_hogg,
    var_names="beta",
    kind="kde",
    divergences=True,
    marginals=True,
    marginal_kwargs=marginal_kwargs,
    kde_kwargs=kde_kwargs,
    ax=ax,
    show=True,
)
ax[0, 0].get_figure().suptitle(
    "Posterior joint distributions" + "\nOLS, StudentT, and Hogg (inliers)"
);
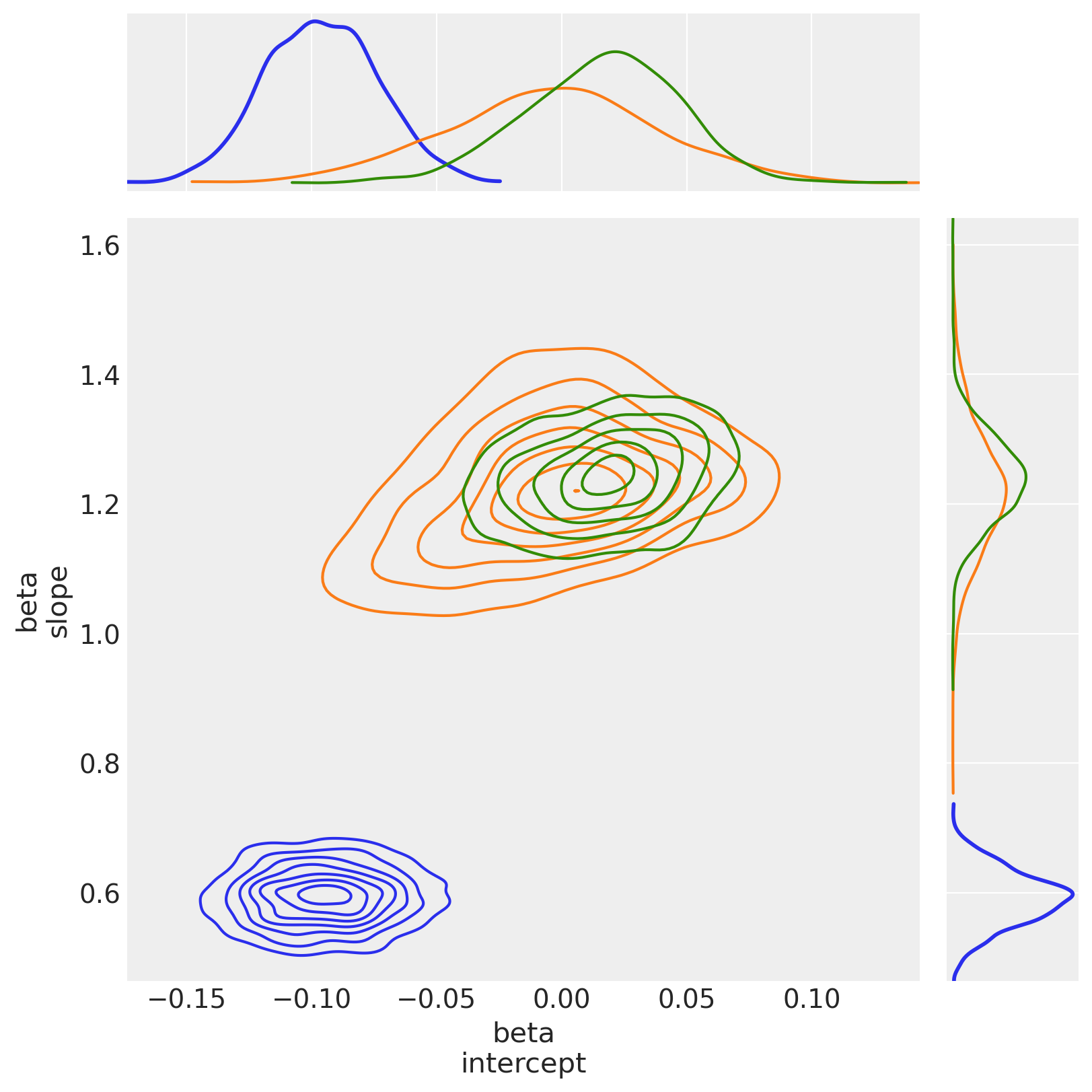
../../../_images/b0e0003e6f3f0c5c073a482b288e02a9f0e36101246ed65fda5dd88be980578e.png

观察：

  • The hogg_inlier 和 studentt 模型在 b0_intercept 和 b1_slope 上收敛到相似的范围，表明（未显示的）hogg_outlier 模型可能与 studentt 模型的胖尾部分执行类似的工作：允许在数据点中远离主要线性分布的地方具有更大的对数概率。

  • 正如预期的那样，（因为它是正态分布）hogg_inlier 后验分布具有更薄的尾部，并且更多的概率质量集中在中心值附近

  • The hogg_inlier 模型似乎也离 ols 和 studentt 模型在 b0_intercept 上的距离更远了，这表明异常值确实扭曲了该特定维度。

5.3 声明异常值#

5.3.1 查看内点/异常点的预测范围#

在每个跟踪步骤中，每个数据点可能是正常点或异常点。我们希望数据点在一种状态或另一种状态上花费的时间不相等，因此让我们来看一下每个数据点的20个状态的简单计数。

dfm_outlier_results = trc_hogg.posterior.is_outlier.to_dataframe().reset_index()

with plt.rc_context({"figure.constrained_layout.use": False}):
    gd = sns.catplot(
        y="datapoint_id",
        x="is_outlier",
        data=dfm_outlier_results,
        kind="point",
        join=False,
        height=6,
        aspect=2,
    )
_ = gd.fig.axes[0].set(xlim=(-0.05, 1.05), xticks=np.arange(0, 1.1, 0.1))
_ = gd.fig.axes[0].axvline(x=0, color="b", linestyle=":")
_ = gd.fig.axes[0].axvline(x=1, color="r", linestyle=":")
_ = gd.fig.axes[0].yaxis.grid(True, linestyle="-", which="major", color="w", alpha=0.4)
_ = gd.fig.suptitle(
    ("For each datapoint, distribution of outlier classification " + "over the trace"),
    y=1.04,
    fontsize=16,
)
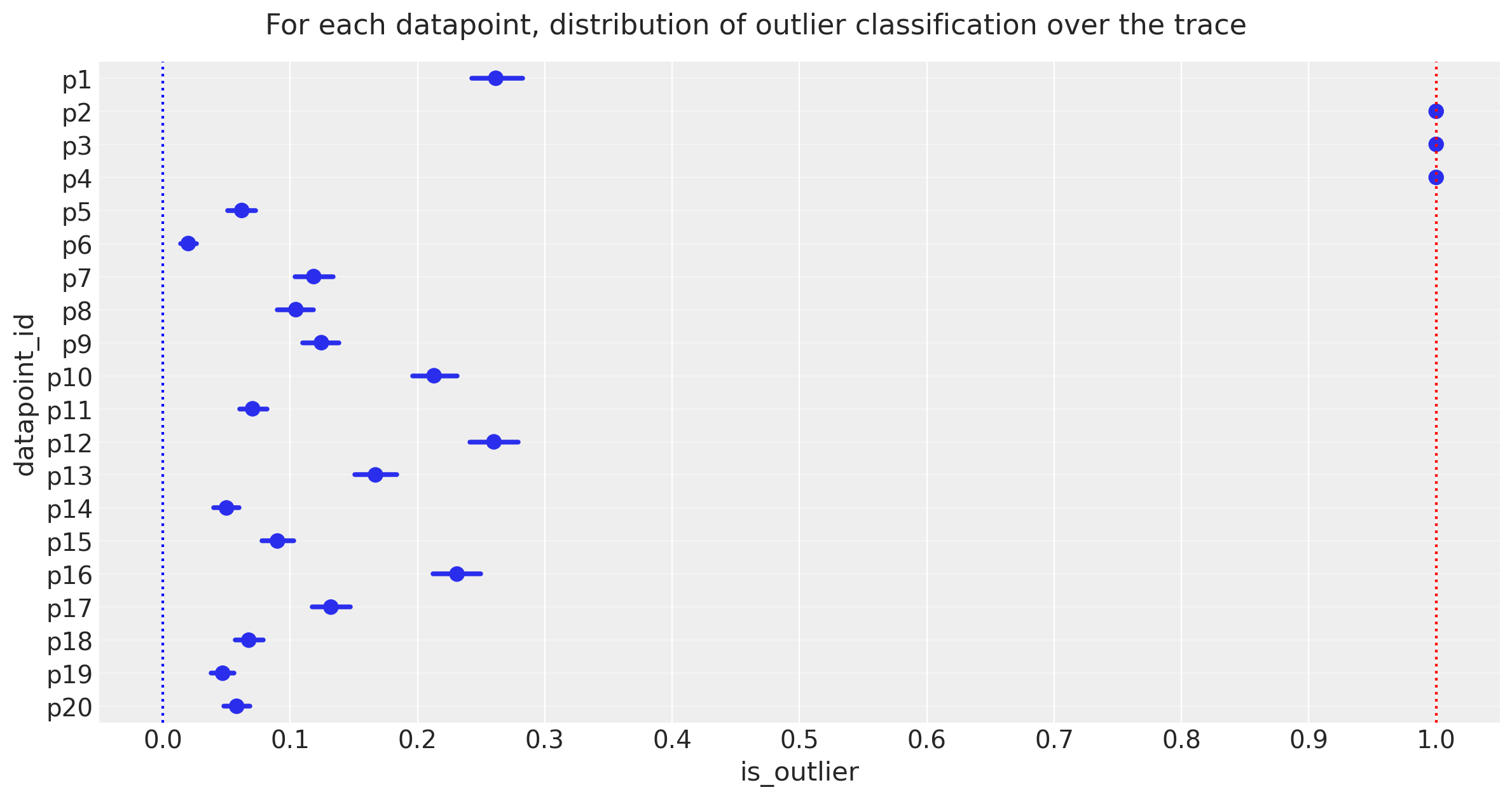
../../../_images/84ec3879702eef692ef34fc3913b9a4107051c650790c9e0f2ed309eaf25bf82.png

观察：

  • 上图显示了在轨迹中每个数据点被标记为异常值的样本比例，以百分比表示。

  • 3个点 [p2, p3, p4] 花费超过95%的时间作为异常值

  • 注意frac_outliers ~ 0.27的平均后验值，对应于大约5或6个20个数据点：我们可能会调查数据点[p1, p12, p16]，看看它们是否倾向于成为异常值

我们选择的95%截止值是主观且任意的，但我目前更喜欢它，所以让我们将这3个数据点声明为异常值，并看看它与Jake Vanderplas的异常值相比如何，后者是以稍微不同的方式声明的，即均值高于0.68的点。

5.3.2 声明异常值#

注意：

  • 我将声明异常值为在5%分位数截止点处值为1的数据点，即在5到100的分位数范围内，它们的值为1。

  • 亲自尝试将cutoff值调整为更大的值，这将导致异常值的客观排名。

cutoff = 0.05
dfhoggs["classed_as_outlier"] = (
    trc_hogg.posterior["is_outlier"].quantile(cutoff, dim=("chain", "draw")) == 1
)
dfhoggs["classed_as_outlier"].value_counts()

False    17
True      3
Name: classed_as_outlier, dtype: int64

同时添加需要调查的点的标志。将使用此标志来标注最终图表

dfhoggs["annotate_for_investigation"] = (
    trc_hogg.posterior["is_outlier"].quantile(0.75, dim=("chain", "draw")) == 1
)
dfhoggs["annotate_for_investigation"].value_counts()

False    15
True      5
Name: annotate_for_investigation, dtype: int64

5.4 OLS、StudentT 和 Hogg “信号与噪声” 的后验预测图#

import xarray as xr

x = xr.DataArray(np.linspace(-3, 3, 10), dims="plot_dim")

# evaluate outlier posterior distribution for plotting
trc_hogg.posterior["outlier_mean"] = trc_hogg.posterior["y_est_out"].broadcast_like(x)

# evaluate model (inlier) posterior distributions for all 3 models
lm = lambda beta, x: beta.sel(coefs="intercept") + beta.sel(coefs="slope") * x

trc_ols.posterior["y_mean"] = lm(trc_ols.posterior["beta"], x)
trc_studentt.posterior["y_mean"] = lm(trc_studentt.posterior["beta"], x)
trc_hogg.posterior["y_mean"] = lm(trc_hogg.posterior["beta"], x)

with plt.rc_context({"figure.constrained_layout.use": False}):
    gd = sns.FacetGrid(
        dfhoggs,
        height=7,
        hue="classed_as_outlier",
        hue_order=[True, False],
        palette="Set1",
        legend_out=False,
    )

# plot hogg outlier posterior distribution
outlier_mean = az.extract(trc_hogg, var_names="outlier_mean", num_samples=400)
gd.ax.plot(x, outlier_mean, color="C3", linewidth=0.5, alpha=0.2, zorder=1)

# plot the 3 model (inlier) posterior distributions
y_mean = az.extract(trc_ols, var_names="y_mean", num_samples=200)
gd.ax.plot(x, y_mean, color="C0", linewidth=0.5, alpha=0.2, zorder=2)

y_mean = az.extract(trc_studentt, var_names="y_mean", num_samples=200)
gd.ax.plot(x, y_mean, color="C1", linewidth=0.5, alpha=0.2, zorder=3)

y_mean = az.extract(trc_hogg, var_names="y_mean", num_samples=200)
gd.ax.plot(x, y_mean, color="C2", linewidth=0.5, alpha=0.2, zorder=4)

# add legend for regression lines plotted above
line_legend = plt.legend(
    [
        Line2D([0], [0], color="C3"),
        Line2D([0], [0], color="C2"),
        Line2D([0], [0], color="C1"),
        Line2D([0], [0], color="C0"),
    ],
    ["Hogg Inlier", "Hogg Outlier", "Student-T", "OLS"],
    loc="lower right",
    title="Posterior Predictive",
)
gd.ax.add_artist(line_legend)

# plot points
_ = gd.map(
    plt.errorbar,
    "x",
    "y",
    "sigma_y",
    "sigma_x",
    marker="o",
    ls="",
    markeredgecolor="w",
    markersize=10,
    zorder=5,
).add_legend()
gd.ax.legend(loc="upper left", title="Outlier Classification")

# annotate the potential outliers
for idx, r in dfhoggs.loc[dfhoggs["annotate_for_investigation"]].iterrows():
    _ = gd.ax.annotate(
        text=idx,
        xy=(r["x"], r["y"]),
        xycoords="data",
        xytext=(7, 7),
        textcoords="offset points",
        color="k",
        zorder=4,
    )

## create xlims ylims for plotting
x_ptp = np.ptp(dfhoggs["x"].values) / 3.3
y_ptp = np.ptp(dfhoggs["y"].values) / 3.3
xlims = (dfhoggs["x"].min() - x_ptp, dfhoggs["x"].max() + x_ptp)
ylims = (dfhoggs["y"].min() - y_ptp, dfhoggs["y"].max() + y_ptp)
gd.ax.set(ylim=ylims, xlim=xlims)
gd.fig.suptitle(
    (
        "Standardized datapoints in Hogg 2010 dataset, showing "
        "posterior predictive fit for 3 models:\nOLS, StudentT and Hogg "
        '"Signal vs Noise" (inlier vs outlier, custom likelihood)'
    ),
    y=1.04,
    fontsize=14,
);
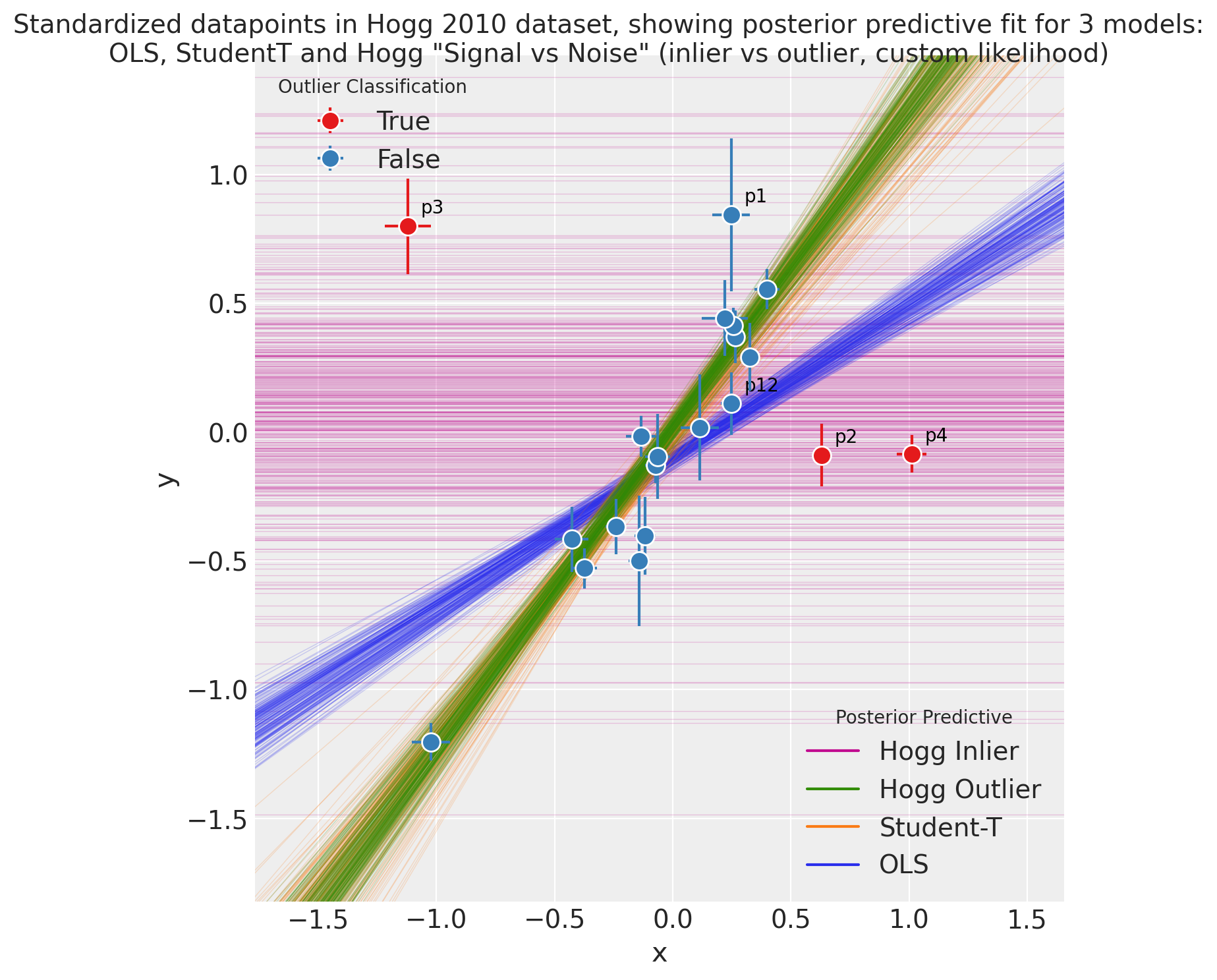
../../../_images/bc5da58b9a0f8fd700ec8f6633749b4df034d83bcc70ac92205b24a240bce61e.png

观察：

后验预测拟合为：

  • 显示的OLS模型以绿色表示，正如预期的那样，它似乎并没有很好地拟合我们的大多数数据点，受异常值的影响而偏斜。

  • 在橙色中显示的学生-T模型确实很好地拟合了数据点的“主轴”，忽略了异常值

  • 该Hogg 信号与噪声模型分为两部分展示：

    • 蓝色用于内点，很好地拟合了数据点的“主轴”，忽略了异常值

    • 红色用于异常值的方差非常大，并且为“异常值”点分配了比蓝色内值模型更多的对数似然值

我们看到Hogg 信噪比模型也给出了关于哪些数据点是异常值的具体估计：

  • 17 个“内点”数据点，以蓝色表示，并且

  • 3 个“异常值”数据点显示为红色。

  • 从简单的视觉检查来看，分类似乎是公平的，并且与Jake Vanderplas的发现一致。

  • 我已经将这些红色和最外围的内点标注出来，以帮助视觉调查

总体：

  • 这个Hogg 信号与噪声模型如承诺的那样运行，产生了一个稳健的回归估计，并明确标记了内点/离群点，但是

  • 这个Hogg 信号与噪声模型相当复杂，尽管回归看起来很稳健，但跟踪图显示了许多分歧，模型可能不稳定

  • 如果你只是想要一个没有内点/外点标记的稳健回归，学生-T模型可能是一个很好的折衷方案，提供了一个简单的模型，快速的采样，以及非常相似的估计。

参考资料#

[1] (1,2)

David W. Hogg, Jo Bovy, 和 Dustin Lang. 数据分析方法：拟合模型到数据。2010年。arXiv:1008.4686。

[2]

Željko Ivezić, Andrew J. Connolly, Jacob T. VanderPlas, 和 Alexander Gray. 天文学中的统计学、数据挖掘和机器学习：调查数据分析的实用Python指南. 普林斯顿大学出版社, 2014. ISBN 9781400848911. doi:10.1515/9781400848911.

[3]

J.T. Vanderplas, A.J. Connolly, Ž. Ivezić, 和 A. Gray. 天体物理学机器学习导论：astroml 简介。在 智能数据理解会议 (CIDU) 上，47–54。2012年10月。doi:10.1109/CIDU.2012.6382200。

[4]

安德鲁·盖尔曼。通过将输入除以两个标准差来缩放回归输入。《医学统计》，27(15):2865–2873, 2008年。doi:10.1002/sim.3107。

作者#

  • 由Jon Sedar（jonsedar）于2015年12月创作并改编为此集合。它最初发布在jonsedar/pymc3_examples

  • 由Thomas Wiecki更新（twiecki）于2018年7月

    • 使用 pm.Normal.dist().logp() 和 pm.Potential() 重新表述异常值模型

  • 更新于 Jon Sedar 于 2019年11月

    • 在StudentT模型中重新表述nu以提高效率，放弃显式使用theano共享变量，总体上改进绘图/解释/布局

  • 更新于 Jon Sedar，2020年5月

    • 整理语言、格式、图表和警告，并使用 pymc=3.8, arviz=0.7 重新运行

  • 更新者：Raul Maldonado (CloudChaoszero) 于2021年4月

    • 整理语言，格式化，将 MultiTrace 对象设置为 arviz.InferenceData 对象，运行在 pymc=3.11, arviz=0.11.0

  • 更新于2021年5月，作者：Raul Maldonado

    • 从 Matplotlib 显式调用 Arviz 可视化更新可视化对象，运行在 pymc=3.11, arviz=0.11.0

  • 更新于2021年11月，作者：Oriol Abril

  • 更新至 PyMC v5 并使用 az.extract，由 Benjamin Vincent 于 2023 年 2 月更新（pymc-examples#522）

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p theano,xarray

Last updated: Sun Feb 05 2023

Python implementation: CPython
Python version       : 3.10.9
IPython version      : 8.9.0

theano: not installed
xarray: 2023.1.0

numpy     : 1.24.1
arviz     : 0.14.0
pandas    : 1.5.3
pymc      : 5.0.1
seaborn   : 0.12.2
scipy     : 1.10.0
matplotlib: 3.6.3
xarray    : 2023.1.0

Watermark: 2.3.1