使用块更新的Lasso回归#

%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v4.0.0b2

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

有时，同时更新一组参数非常有用。例如，高度相关的变量通常适合一起更新。在 PyMC 中，块更新非常简单。这将以 pymc.sample 的参数 step 为例进行演示。

这里我们有一个LASSO回归模型，其中两个系数高度相关。通常情况下，我们会将系数参数定义为一个单一的随机变量，但在这里我们将它们分别定义，以展示如何进行块更新。

首先我们生成一些假数据。

x = rng.standard_normal(size=(3, 30))
x1 = x[0] + 4
x2 = x[1] + 4
noise = x[2]
y_obs = x1 * 0.2 + x2 * 0.3 + noise

然后定义随机变量。

lam = 3000

with pm.Model() as model:
    sigma = pm.Exponential("sigma", 1)
    tau = pm.Uniform("tau", 0, 1)
    b = lam * tau
    beta1 = pm.Laplace("beta1", 0, b)
    beta2 = pm.Laplace("beta2", 0, b)

    mu = x1 * beta1 + x2 * beta2

    y = pm.Normal("y", mu=mu, sigma=sigma, observed=y_obs)

对于大多数采样器，包括 pymc.Metropolis 和 pymc.HamiltonianMC，只需传递一个要作为块采样的变量列表。这适用于标量和数组参数。

with model:
    step1 = pm.Metropolis([beta1, beta2])

    step2 = pm.Slice([sigma, tau])

    idata = pm.sample(draws=10000, step=[step1, step2])

Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>CompoundStep
>>Metropolis: [beta1]
>>Metropolis: [beta2]
>CompoundStep
>>Slice: [sigma]
>>Slice: [tau]

100.00% [44000/44000 00:36<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 37 seconds.
The number of effective samples is smaller than 10% for some parameters.

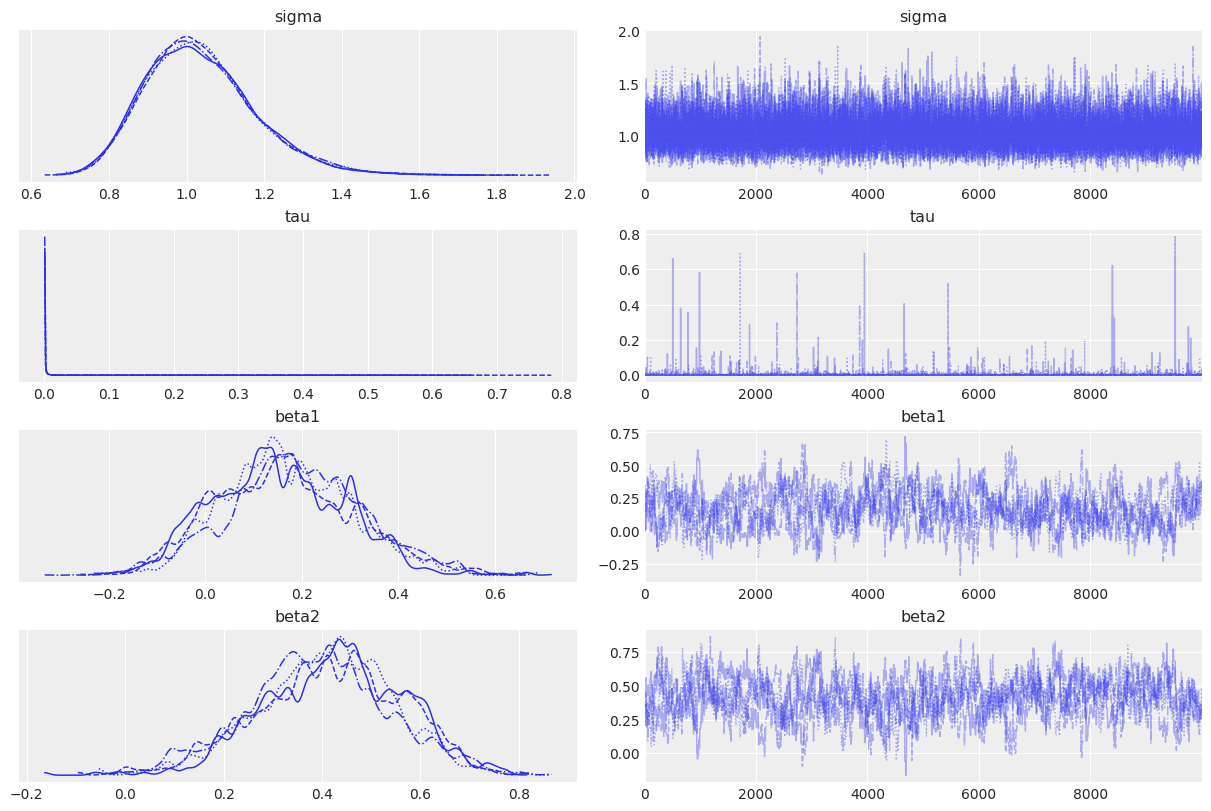
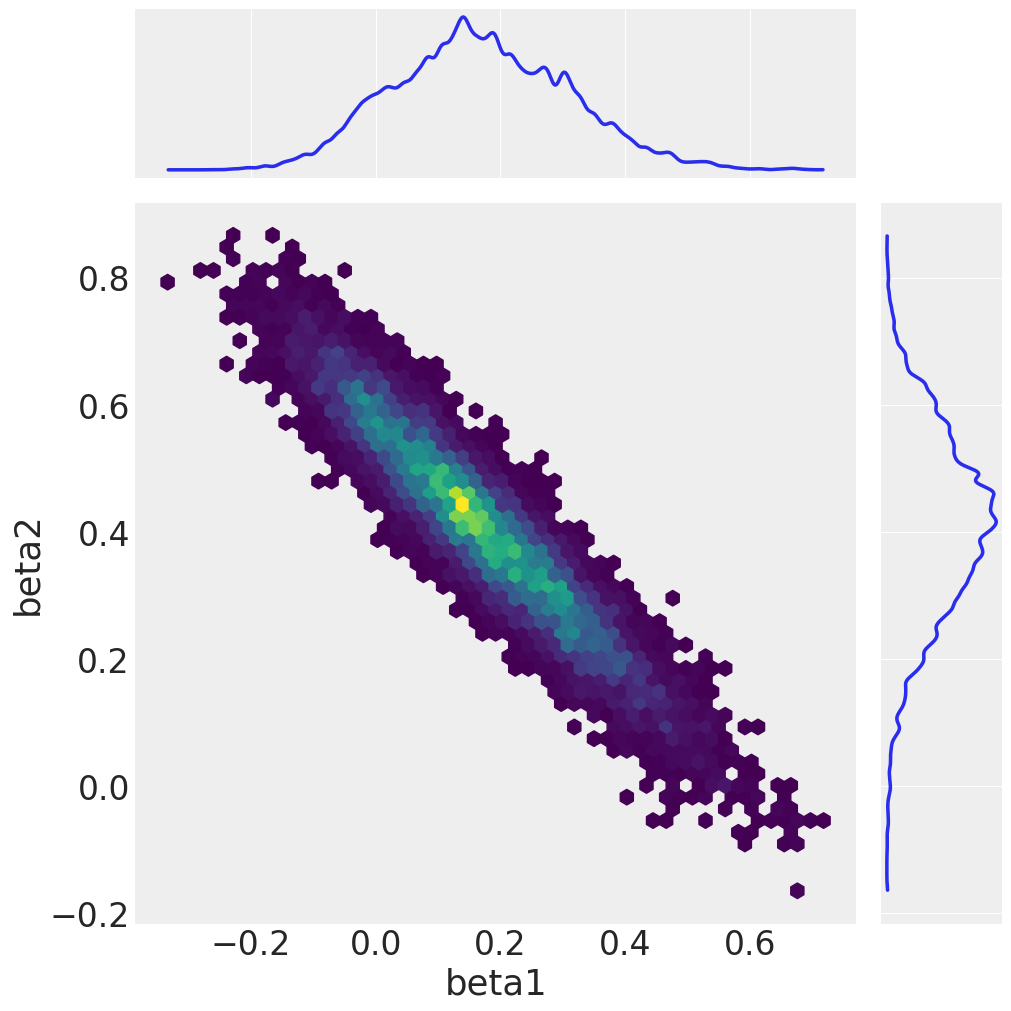
我们通过绘制采样的边缘分布和beta1与beta2的联合分布来总结。

az.plot_trace(idata);

../../../_images/0e88fba95c22b32165ed71adbc218847af2815a3f51302229e16df872cda552a.png

az.plot_pair(
    idata,
    var_names=["beta1", "beta2"],
    kind="hexbin",
    marginals=True,
    figsize=(10, 10),
    gridsize=50,
)

array([[<AxesSubplot:>, None],
       [<AxesSubplot:xlabel='beta1', ylabel='beta2'>, <AxesSubplot:>]],
      dtype=object)

../../../_images/2bc755fd8bf0a29be0c099502d53d2097de89708e8fd4c792426392f28773e1f.png

作者#

由Chris Fonnesbeck于2020年12月撰写
更新者 Raul Maldonado 于2021年1月
由Raul Maldonado于2021年3月更新
由 Thomas Wiecki 和 Michael Osthege 使用 PyMC v4 于 2022 年 1 月重新执行（pymc-examples#264）
由 Lorenzo Toniazzi 于2022年2月更新（pymc-examples#279）

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray

Last updated: Thu Mar 03 2022

Python implementation: CPython
Python version       : 3.9.10
IPython version      : 8.0.1

pytensor: 2.3.2
aeppl : 0.0.18
xarray: 2022.3.0

pymc      : 4.0.0b2
matplotlib: 3.5.1
numpy     : 1.21.5
arviz     : 0.11.4

Watermark: 2.3.0

分类

标签

使用块更新的Lasso回归#

作者#

水印#