使用Euler-Maruyama方案推断SDE的参数#

本笔记本源自为艾克斯-马赛大学系统神经科学研究所的理论神经科学小组准备的演示文稿。

import warnings

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor.tensor as pt
import scipy as sp

# Ignore UserWarnings
warnings.filterwarnings("ignore", category=UserWarning)

RANDOM_SEED = 8927
np.random.seed(RANDOM_SEED)

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")

示例模型#

这是一个标量线性随机微分方程的符号形式

\( dX_t = \lambda X_t + \sigma^2 dW_t \)

使用欧拉-丸山方案进行离散化。

我们可以从这个过程中模拟数据，然后尝试恢复参数。

# parameters
lam = -0.78
s2 = 5e-3
N = 200
dt = 1e-1

# time series
x = 0.1
x_t = []

# simulate
for i in range(N):
    x += dt * lam * x + np.sqrt(dt) * s2 * np.random.randn()
    x_t.append(x)

x_t = np.array(x_t)

# z_t noisy observation
z_t = x_t + np.random.randn(x_t.size) * 5e-3

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))

ax1.plot(x_t[:30], "k", label="$x(t)$", alpha=0.5)
ax1.plot(z_t[:30], "r", label="$z(t)$", alpha=0.5)
ax1.set_title("Transient")
ax1.legend()

ax2.plot(x_t[30:], "k", label="$x(t)$", alpha=0.5)
ax2.plot(z_t[30:], "r", label="$z(t)$", alpha=0.5)
ax2.set_title("All time")
ax2.legend()

plt.tight_layout()

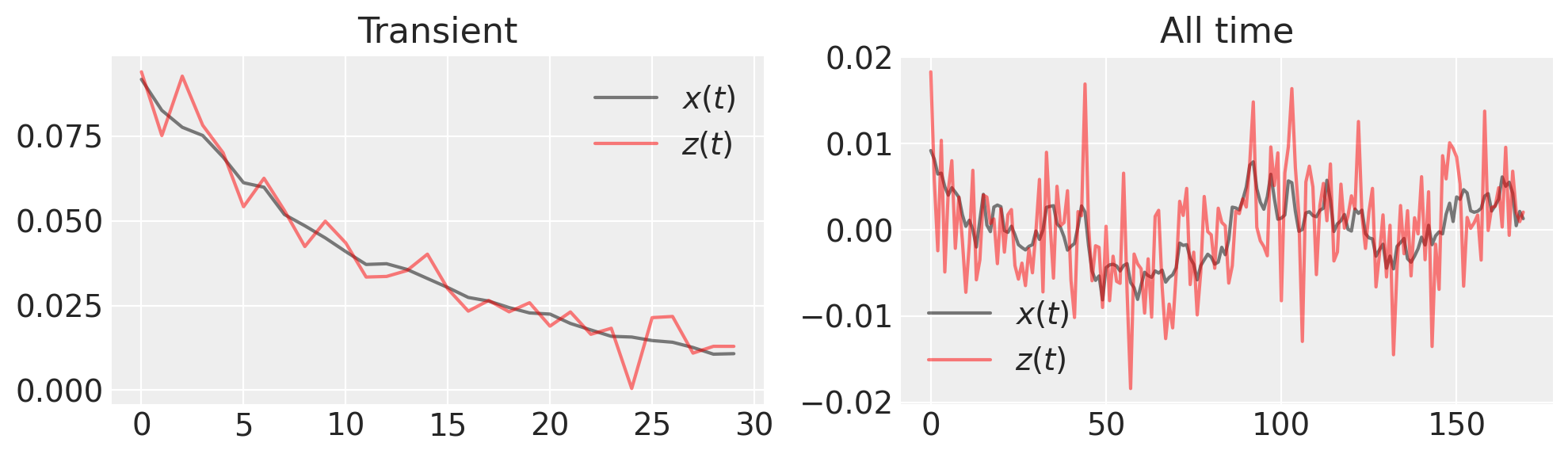
../../../_images/346da134c479657a572ddadb6fca97098efe05fbd219404d0aa1d7f4297dd575.png

我们想要得出什么推论？由于我们已经对生成的时间序列进行了噪声观测，我们需要估计 \(x(t)\) 和 \(\lambda\)。

我们需要提供一个SDE函数，该函数返回漂移和扩散系数。

def lin_sde(x, lam, s2):
    return lam * x, s2

概率模型由漂移参数 lam 的先验、扩散系数 s、潜在的欧拉-丸山过程 xh 以及描述噪声观测的似然 zh 组成。我们将假设我们知道观测噪声。

with pm.Model() as model:
    # uniform prior, but we know it must be negative
    l = pm.HalfCauchy("l", beta=1)
    s = pm.Uniform("s", 0.005, 0.5)

    # "hidden states" following a linear SDE distribution
    # parametrized by time step (det. variable) and lam (random variable)
    xh = pm.EulerMaruyama("xh", dt=dt, sde_fn=lin_sde, sde_pars=(-l, s**2), shape=N, initval=x_t)

    # predicted observation
    zh = pm.Normal("zh", mu=xh, sigma=5e-3, observed=z_t)

一旦模型构建完成，我们进行推理，这里是通过nutpie实现的NUTS算法，这将非常快速。

with model:
    trace = pm.sample(nuts_sampler="nutpie", random_seed=RANDOM_SEED, target_accept=0.99)

采样器进度

总链数: 4

活跃链：0

完成的链： 4

现在进行采样

预计完成时间： now

Draws	Step Size	Gradients/Draw
2000	0.06	255
2000	0.06	127
2000	0.07	255
2000	0.06	191

接下来，我们绘制后验样本的一些基本统计数据，

plt.figure(figsize=(10, 3))
plt.subplot(121)
plt.plot(
    trace.posterior.quantile((0.025, 0.975), dim=("chain", "draw"))["xh"].values.T,
    "k",
    label=r"$\hat{x}_{95\%}(t)$",
)
plt.plot(x_t, "r", label="$x(t)$")
plt.legend()

plt.subplot(122)
plt.hist(-1 * az.extract(trace.posterior)["l"], 30, label=r"$\hat{\lambda}$", alpha=0.5)
plt.axvline(lam, color="r", label=r"$\lambda$", alpha=0.5)
plt.legend();

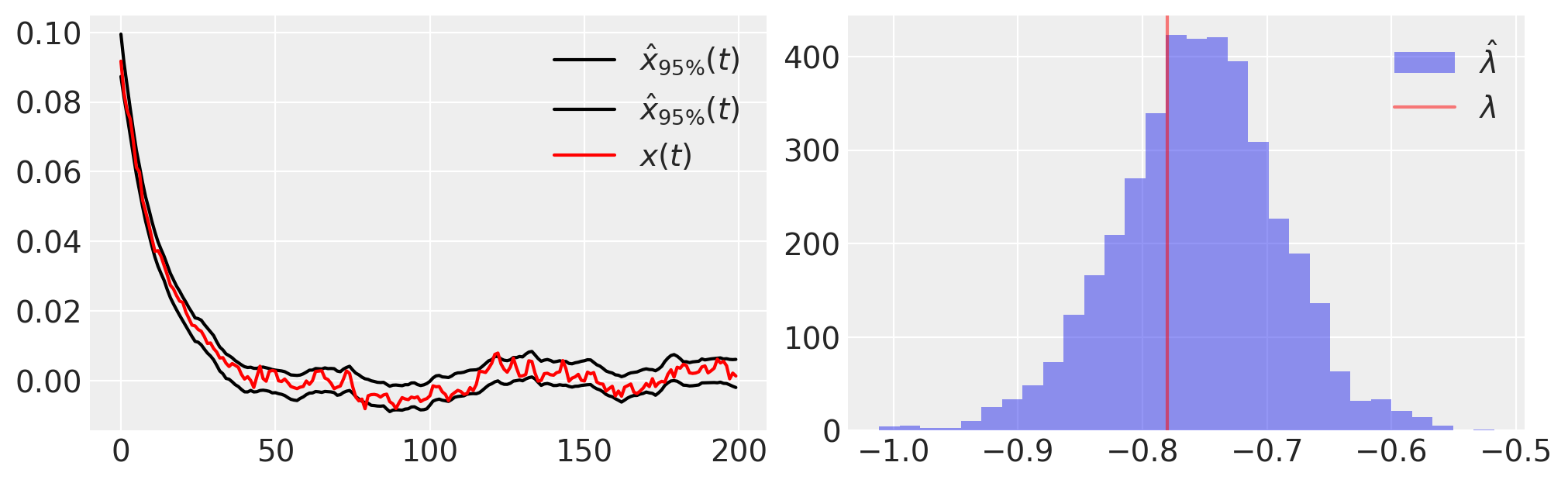
../../../_images/2b776f5df4e8a6fc9178a643b8931d320aaddec8810833d406577ab52256f51a.png

一个模型可以精确地拟合数据，但仍然可能是错误的；我们需要使用后验预测检查来评估在我们的拟合模型下，数据是否可能是合理的。

换句话说，我们

假设模型是正确的
模拟新观测值
检查新观测值是否与原始数据相符

# generate trace from posterior
with model:
    pm.sample_posterior_predictive(trace, extend_inferencedata=True)

Sampling: [zh]

plt.figure(figsize=(10, 3))
plt.plot(
    trace.posterior_predictive.quantile((0.025, 0.975), dim=("chain", "draw"))["zh"].values.T,
    "k",
    label=r"$z_{95\% PP}(t)$",
)
plt.plot(z_t, "r", label="$z(t)$")
plt.legend();

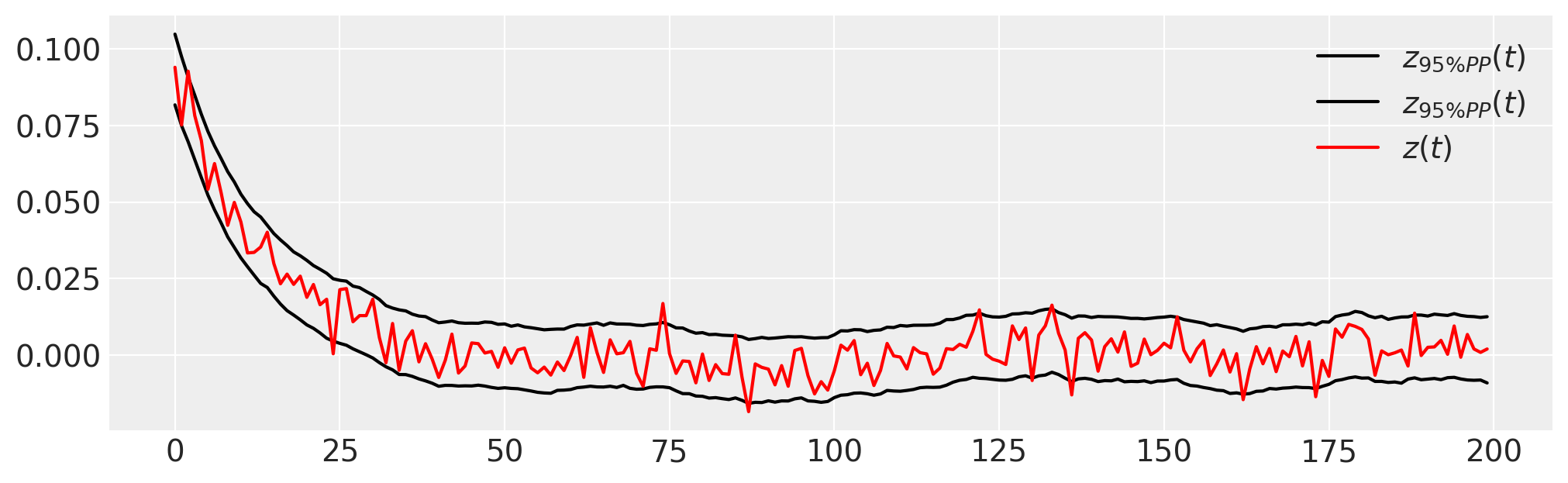
../../../_images/c3ab276d76f68bb69a60d7c6fdb857d53f8146040f2d399bfeb2e813da35270b.png

注意，初始条件也会被估计，并且大多数观测数据 \(z(t)\) 位于PPC的95%区间内。

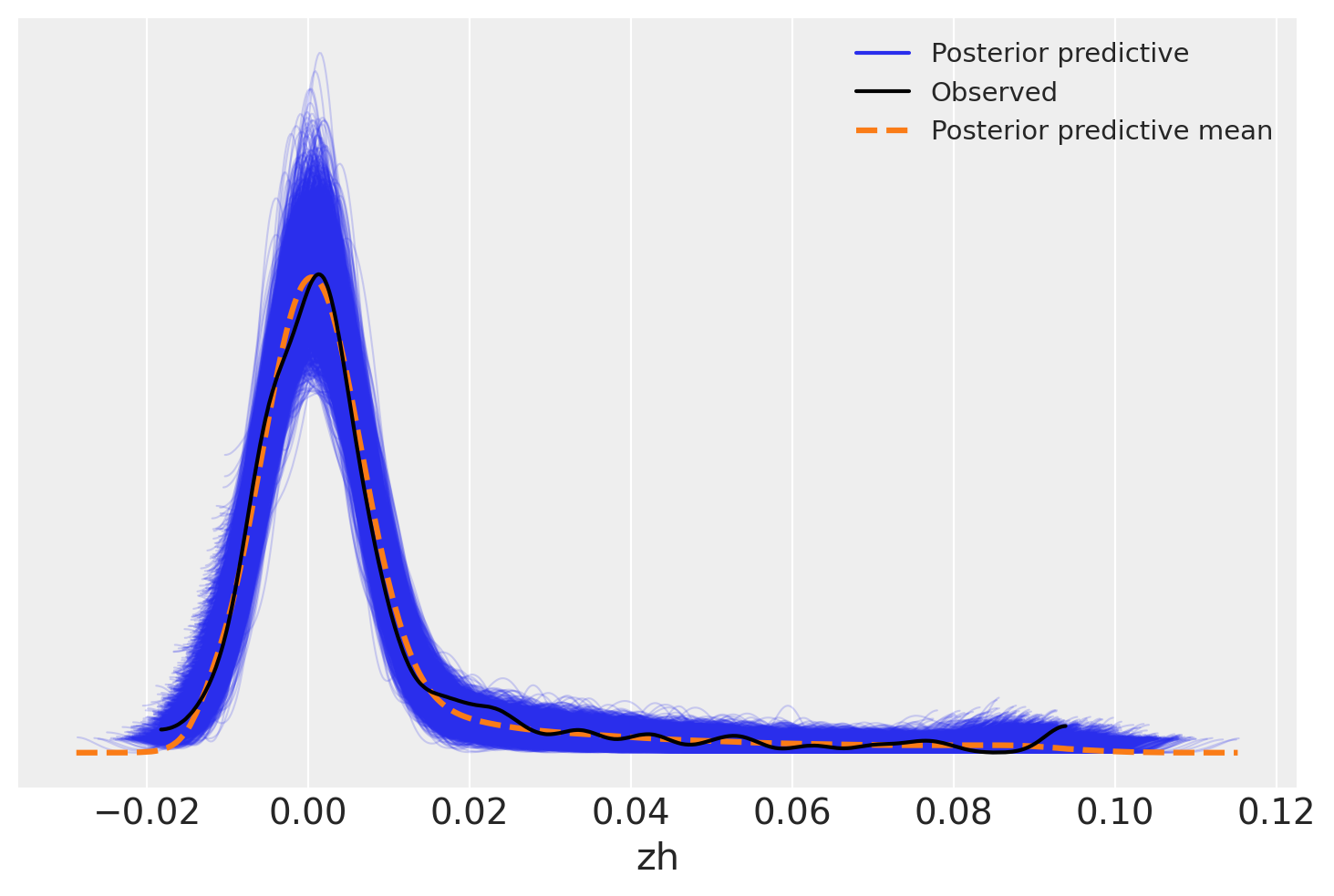
另一种方法是查看相对于观测数据的采样分布的抽取结果。这也显示了在整个观测范围内的良好拟合——后验预测均值几乎完美地追踪了数据。

az.plot_ppc(trace)

<Axes: xlabel='zh'>

../../../_images/17dbd10994eb4ce8227668e1ac07db814f5dafcdfa684e6c0973c7a231588796.png

作者#

由 @maedoc 于2016年7月撰写
更新至 PyMC v5，由 @fonnesbeck 于 2024 年 9 月

参考资料#

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Tue Sep 24 2024

Python implementation: CPython
Python version       : 3.12.5
IPython version      : 8.27.0

matplotlib: 3.9.2
pytensor  : 2.25.4
numpy     : 1.26.4
arviz     : 0.19.0
pymc      : 5.16.2
scipy     : 1.14.1

Watermark: 2.4.3

分类

标签

使用Euler-Maruyama方案推断SDE的参数#

示例模型#

作者#

参考资料#