随机波动率模型#
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
rng = np.random.RandomState(1234)
az.style.use("arviz-darkgrid")
资产价格具有时变波动性(日收益率的方差)。在某些时期,收益率变化很大,而在其他时期则非常稳定。随机波动模型通过一个潜在的波动变量来模拟这种情况,该变量被建模为一个随机过程。以下模型类似于No-U-Turn Sampler论文中描述的模型,[Hoffman和Gelman,2014]。
这里,\(r\) 是每日收益率序列,\(s\) 是潜在的对数波动率过程。
构建模型#
首先我们加载标准普尔500指数的每日回报,并计算每日对数回报。这些数据来自2008年5月至2019年11月。
try:
returns = pd.read_csv(os.path.join("..", "data", "SP500.csv"), index_col="Date")
except FileNotFoundError:
returns = pd.read_csv(pm.get_data("SP500.csv"), index_col="Date")
returns["change"] = np.log(returns["Close"]).diff()
returns = returns.dropna()
returns.head()
| Close | change | |
|---|---|---|
| Date | ||
| 2008-05-05 | 1407.489990 | -0.004544 |
| 2008-05-06 | 1418.260010 | 0.007623 |
| 2008-05-07 | 1392.569946 | -0.018280 |
| 2008-05-08 | 1397.680054 | 0.003663 |
| 2008-05-09 | 1388.280029 | -0.006748 |
如你所见,波动性似乎随着时间变化很大,但在某些时间段内聚集。例如,2008年的金融危机很容易被识别出来。
fig, ax = plt.subplots(figsize=(14, 4))
returns.plot(y="change", label="S&P 500", ax=ax)
ax.set(xlabel="time", ylabel="returns")
ax.legend();
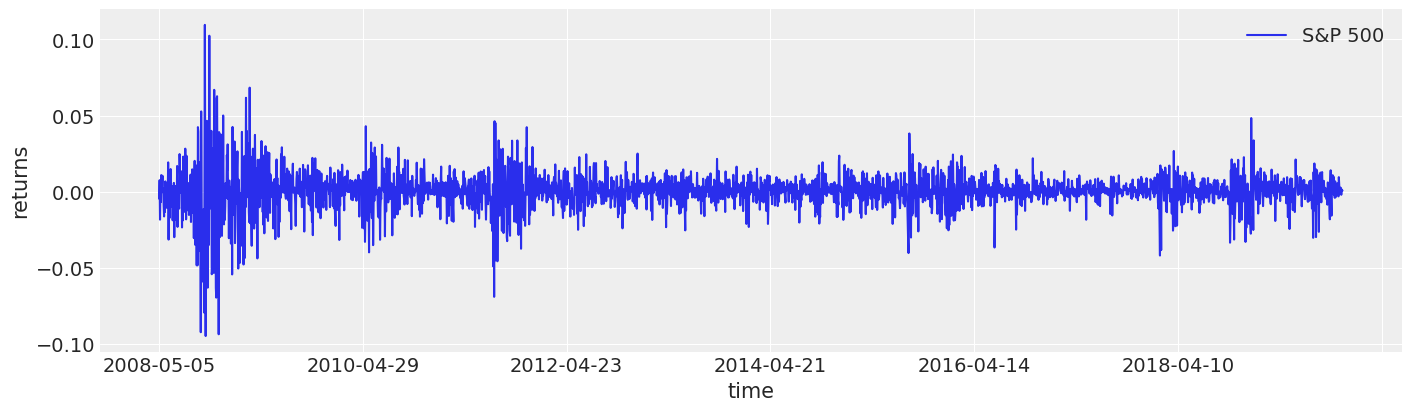
在 PyMC 中指定模型反映了其统计规范。
def make_stochastic_volatility_model(data):
with pm.Model(coords={"time": data.index.values}) as model:
step_size = pm.Exponential("step_size", 10)
volatility = pm.GaussianRandomWalk(
"volatility", sigma=step_size, dims="time", init_dist=pm.Normal.dist(0, 100)
)
nu = pm.Exponential("nu", 0.1)
returns = pm.StudentT(
"returns", nu=nu, lam=np.exp(-2 * volatility), observed=data["change"], dims="time"
)
return model
stochastic_vol_model = make_stochastic_volatility_model(returns)
检查模型#
确保我们的模型符合预期,有两件好事可以做,那就是
查看模型结构。这让我们知道我们指定了所需的先验和所需的连接。它还方便地提醒我们随机变量的大小。
查看先验预测样本。这有助于我们解释我们的先验对数据的含义。
pm.model_to_graphviz(stochastic_vol_model)
with stochastic_vol_model:
idata = pm.sample_prior_predictive(500, random_seed=rng)
prior_predictive = az.extract(idata, group="prior_predictive")
Sampling: [nu, returns, step_size, volatility]
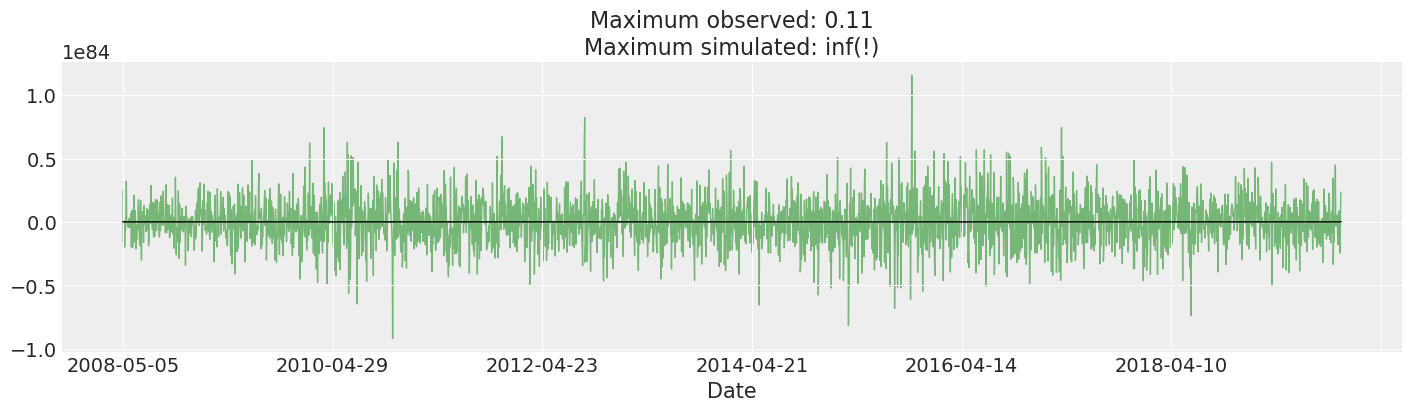
我们绘制并检查先验预测。这比我们观察到的实际回报大得多,实际上是许多数量级。事实上,我挑选了一些抽样结果,以避免图表看起来不合理。这可能表明我们需要改变我们的先验:我们的模型认为合理的回报将违反各种约束,而且幅度非常大:全球所有商品和服务的总价值约为\(\$10^9\),因此我们可能合理地不期望任何超过该数量级的回报。
尽管如此,我们仍然得到了一些合理的结果来拟合这个模型,而且它是标准的,所以我们保持原样。
fig, ax = plt.subplots(figsize=(14, 4))
returns["change"].plot(ax=ax, lw=1, color="black")
ax.plot(
prior_predictive["returns"][:, 0::10],
"g",
alpha=0.5,
lw=1,
zorder=-10,
)
max_observed, max_simulated = np.max(np.abs(returns["change"])), np.max(
np.abs(prior_predictive["returns"].values)
)
ax.set_title(f"Maximum observed: {max_observed:.2g}\nMaximum simulated: {max_simulated:.2g}(!)");
拟合模型#
一旦我们对模型感到满意,我们就可以从后验分布中采样。即使使用NUTS,这个模型的拟合也有点棘手,所以我们比默认情况下采样和调整的时间稍长一些。
with stochastic_vol_model:
idata.extend(pm.sample(random_seed=rng))
posterior = az.extract(idata)
posterior["exp_volatility"] = np.exp(posterior["volatility"])
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 113 seconds.
with stochastic_vol_model:
idata.extend(pm.sample_posterior_predictive(idata, random_seed=rng))
posterior_predictive = az.extract(idata, group="posterior_predictive")
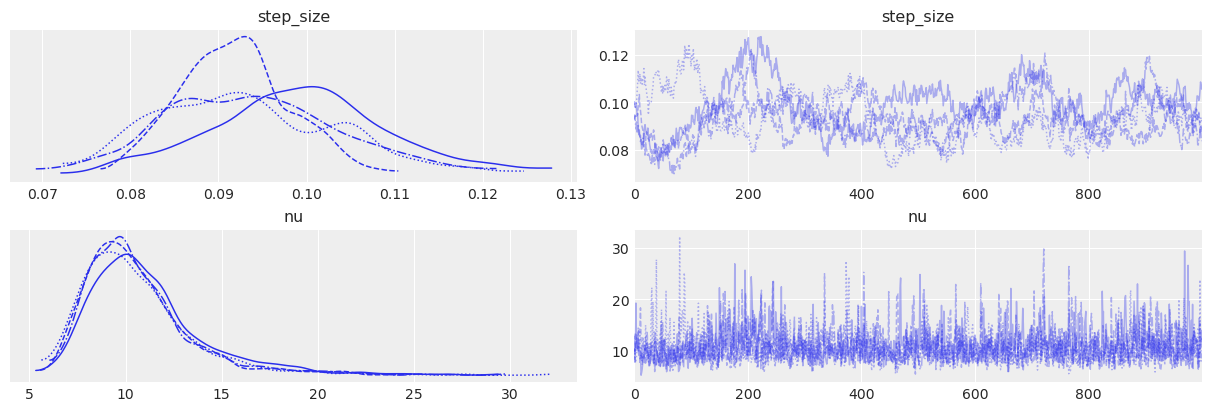
请注意,step_size 参数看起来并不完美:不同的链看起来有些不同。这再次表明我们的模型存在一些弱点:允许 step_size 随时间变化可能是有意义的,尤其是在这 11 年的时间跨度内。
az.plot_trace(idata, var_names=["step_size", "nu"]);
现在我们可以查看标准普尔500指数收益率随时间变化的后验波动率估计。
fig, ax = plt.subplots(figsize=(14, 4))
y_vals = posterior["exp_volatility"]
x_vals = y_vals.time.astype(np.datetime64)
plt.plot(x_vals, y_vals, "k", alpha=0.002)
ax.set_xlim(x_vals.min(), x_vals.max())
ax.set_ylim(bottom=0)
ax.set(title="Estimated volatility over time", xlabel="Date", ylabel="Volatility");
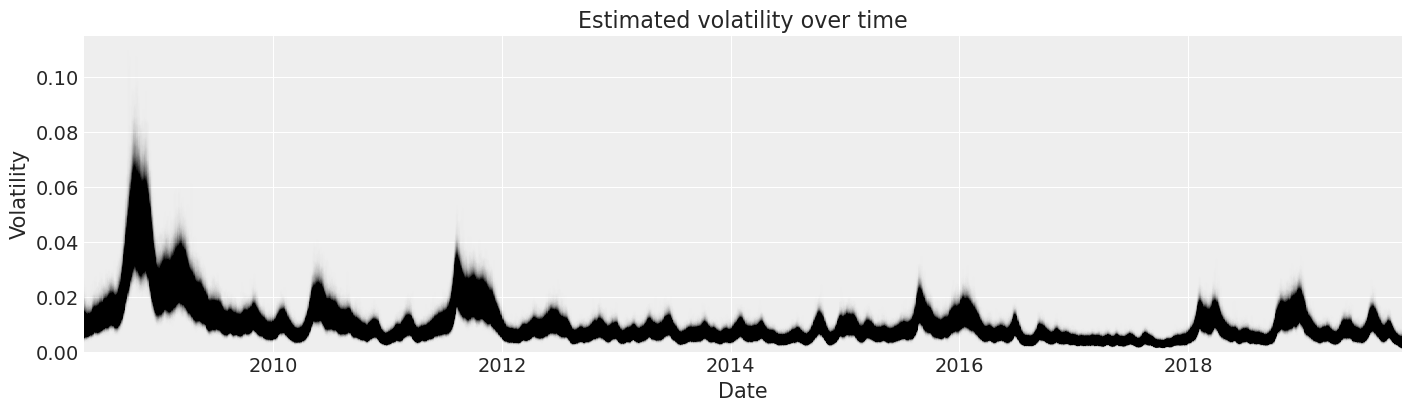
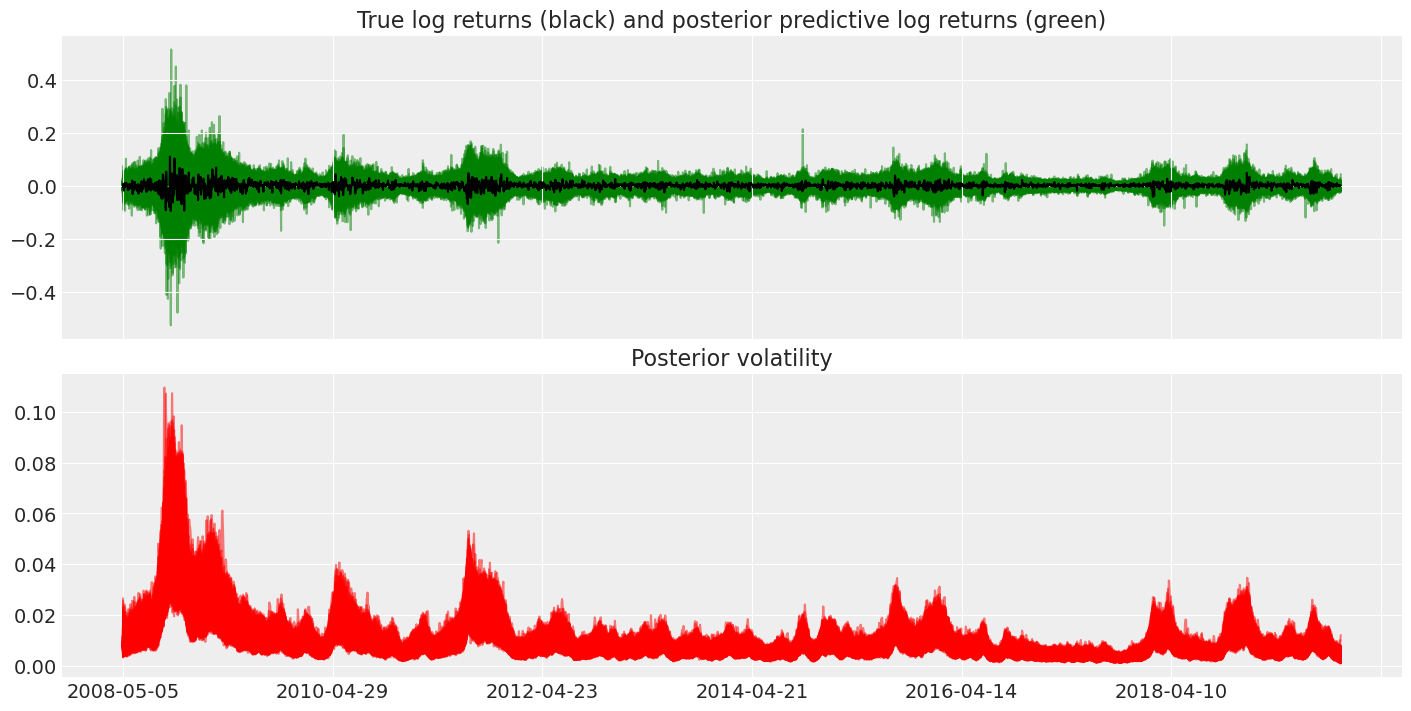
最后,我们可以使用后验预测分布来查看学习到的波动率可能如何影响回报。
fig, axes = plt.subplots(nrows=2, figsize=(14, 7), sharex=True)
returns["change"].plot(ax=axes[0], color="black")
axes[1].plot(posterior["exp_volatility"], "r", alpha=0.5)
axes[0].plot(
posterior_predictive["returns"],
"g",
alpha=0.5,
zorder=-10,
)
axes[0].set_title("True log returns (black) and posterior predictive log returns (green)")
axes[1].set_title("Posterior volatility");
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray
Last updated: Sun Feb 05 2023
Python implementation: CPython
Python version : 3.10.9
IPython version : 8.9.0
pytensor: 2.8.11
aeppl : not installed
xarray : 2023.1.0
arviz : 0.14.0
pymc : 5.0.1
matplotlib: 3.6.3
numpy : 1.24.1
pandas : 1.5.3
Watermark: 2.3.1
参考资料#
Matthew Hoffman 和 Andrew Gelman。无 U 形转弯采样器:在哈密顿蒙特卡洛中自适应设置路径长度。机器学习研究杂志,15:1593–1623,2014。URL: https://dl.acm.org/doi/10.5555/2627435.2638586。