心理测量学中的验证性因子分析和结构方程模型#

“显然，相关性和依赖性的概念比与概率判断相关的数值更基本……用于表示概率信息的语言应该允许对依赖关系进行定性、直接和明确的表达。” - Pearl 在《智能系统中的概率推理》Pearl [1985]

测量数据在心理计量学中通常来源于一个精心设计的调查，旨在针对特定的目标现象。一些直觉上存在但尚未测量的概念，可能在人类行为、动机或情感中起着决定性的作用。心理计量学中主题的相对“模糊性”对科学中追求的方法严谨性起到了催化作用。

调查设计为正确的语调和句子结构的节奏而苦恼。测量尺度经过双重检查以确保其可靠性和正确性。参考文献并完善问题。分析步骤经过合理化并在丰富的建模程序中进行测试。模型架构被定义和完善，以更好地表达数据生成过程中假设的结构。我们将看到这种尽职调查如何导致强大且富有表现力的模型，使我们能够在人类情感的棘手问题上获得可处理性。

在整个过程中，我们借鉴了Roy Levy和Robert J. Mislevy的优秀著作《贝叶斯心理测量建模》。

import warnings

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns

warnings.filterwarnings("ignore", category=RuntimeWarning)
warnings.filterwarnings("ignore", category=UserWarning)

%config InlineBackend.figure_format = 'retina'  # high resolution figures
az.style.use("arviz-darkgrid")
rng = np.random.default_rng(42)

潜在构念与测量#

我们的数据借用了Boris Mayer和Andrew Ellis的工作，可以在这里找到。他们展示了使用lavaan进行CFA和SEM建模。

我们有来自约300名个体的调查反馈，他们回答了关于他们的成长经历、自我效能感和报告的生活满意度的问题。这个生活满意度数据集中的假设依赖结构提出了一种调节关系，涉及与生活满意度、父母和家庭支持以及自我效能相关的分数。设计一个能够合理映射到这些“因素”或主题的调查并非易事，更不用说找到一个能够告诉我们每个因素对生活满意度结果的相对影响的模型了。

首先让我们提取数据并检查一些汇总统计信息。

df = pd.read_csv("../data/sem_data.csv")
df.head()
ID region gender age se_acad_p1 se_acad_p2 se_acad_p3 se_social_p1 se_social_p2 se_social_p3 sup_friends_p1 sup_friends_p2 sup_friends_p3 sup_parents_p1 sup_parents_p2 sup_parents_p3 ls_p1 ls_p2 ls_p3
0 1 west female 13 4.857143 5.571429 4.500000 5.80 5.500000 5.40 6.5 6.5 7.0 7.0 7.0 6.0 5.333333 6.75 5.50
1 2 west male 14 4.571429 4.285714 4.666667 5.00 5.500000 4.80 4.5 4.5 5.5 5.0 6.0 4.5 4.333333 5.00 4.50
2 10 west female 14 4.142857 6.142857 5.333333 5.20 4.666667 6.00 4.0 4.5 3.5 7.0 7.0 6.5 6.333333 5.50 4.00
3 11 west female 14 5.000000 5.428571 4.833333 6.40 5.833333 6.40 7.0 7.0 7.0 7.0 7.0 7.0 4.333333 6.50 6.25
4 12 west female 14 5.166667 5.600000 4.800000 5.25 5.400000 5.25 7.0 7.0 7.0 6.5 6.5 7.0 5.666667 6.00 5.75 
fig, ax = plt.subplots(figsize=(20, 10))
drivers = [c for c in df.columns if not c in ["region", "gender", "age", "ID"]]
corr_df = df[drivers].corr()
mask = np.triu(np.ones_like(corr_df, dtype=bool))
sns.heatmap(corr_df, annot=True, cmap="Blues", ax=ax, center=0, mask=mask)
ax.set_title("Sample Correlations between indicator Metrics")
fig, ax = plt.subplots(figsize=(20, 10))
sns.heatmap(df[drivers].cov(), annot=True, cmap="Blues", ax=ax, center=0, mask=mask)
ax.set_title("Sample Covariances between indicator Metrics");
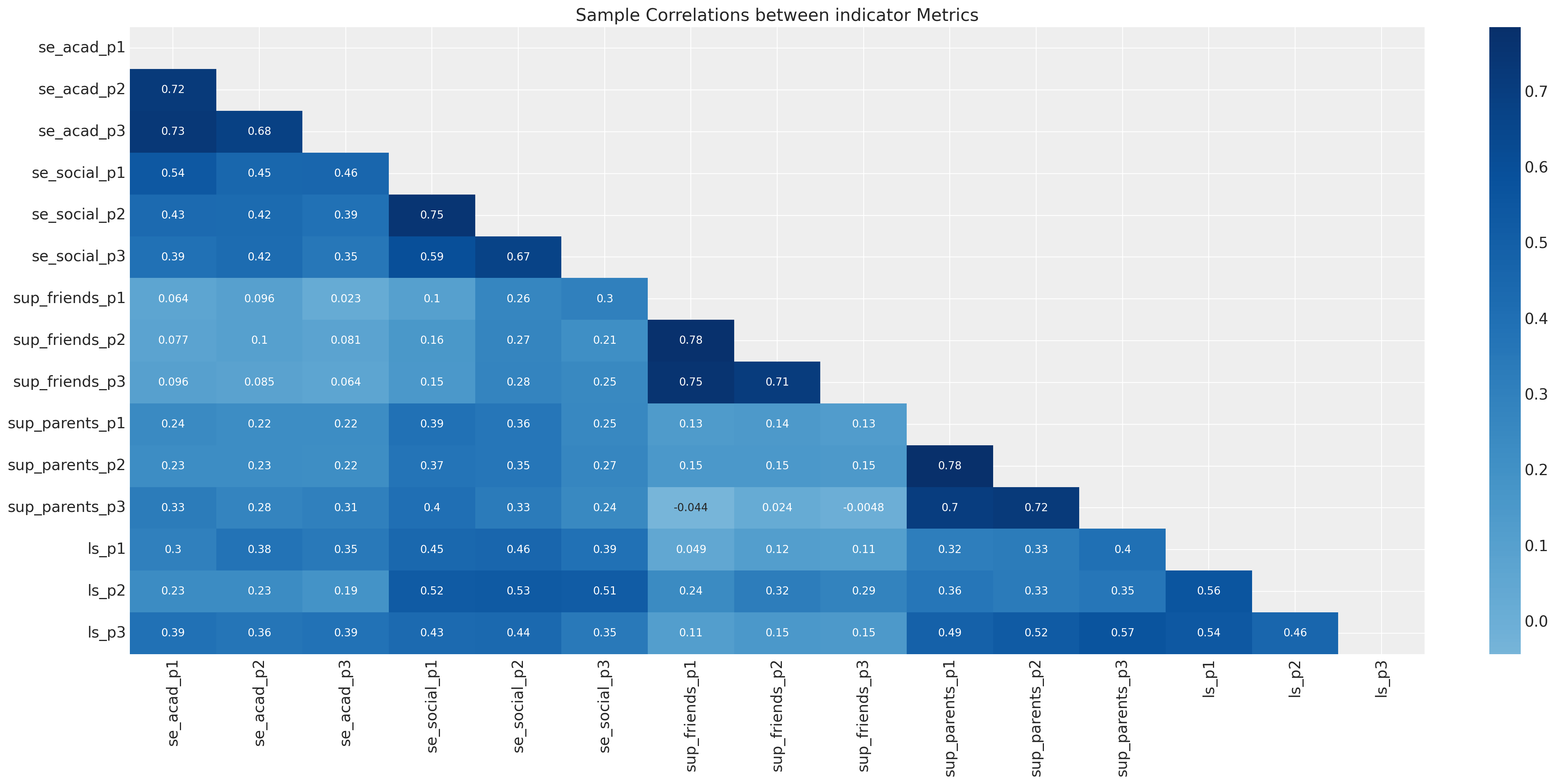
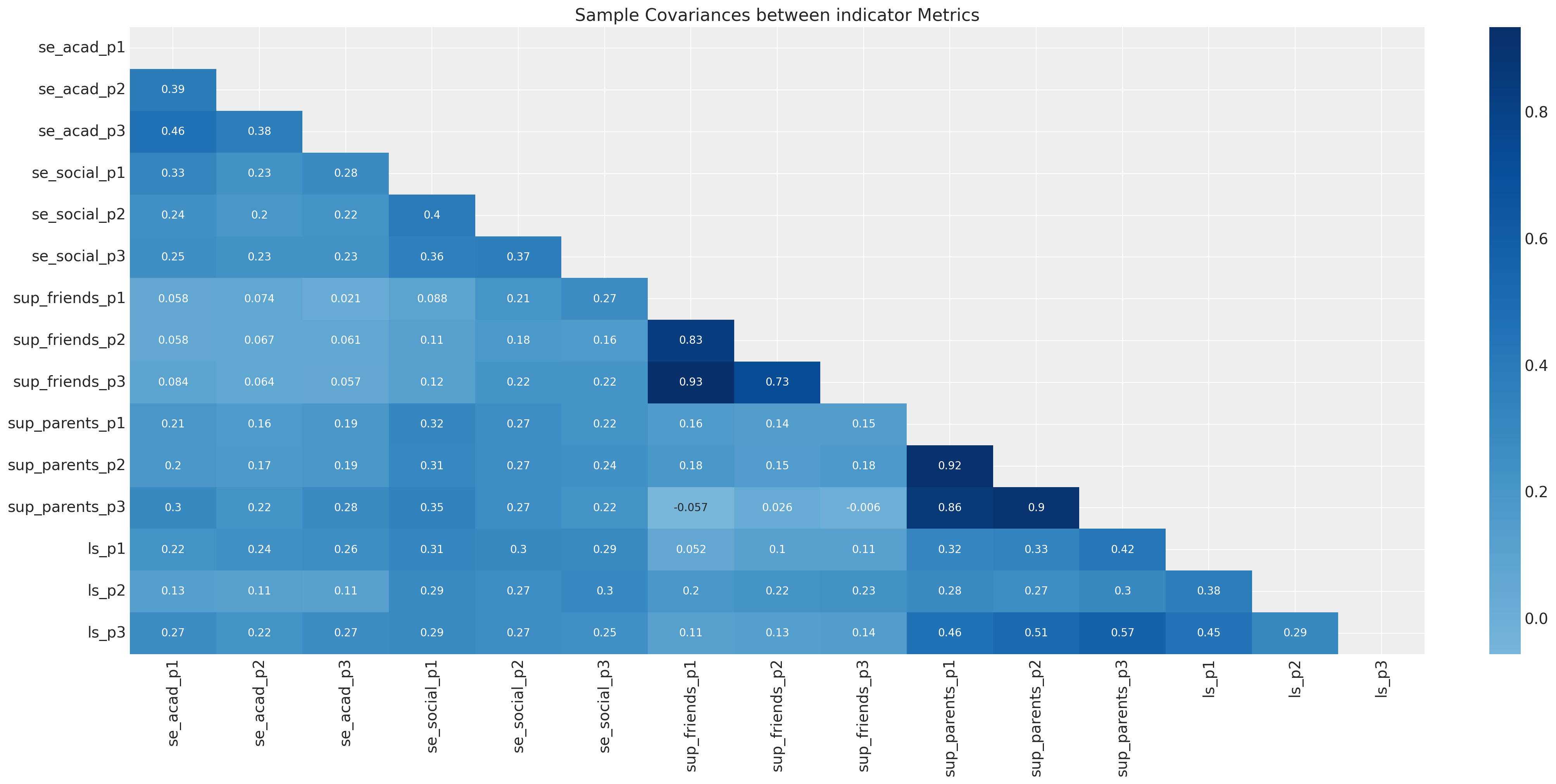
../_images/aebe547ee33a40d30f0b8eee41e262900255ed6a7c431ab65a9927b9e13d1573.png ../_images/48b5e32241718dd511a178f3afaaa08d2a769bab7e76adc4fbcb378bc9aa4645.png

样本协方差矩阵上的这种透镜在传统的SEM建模中很常见。CFA和SEM模型通常通过优化协方差矩阵的参数结构来拟合参数以适应数据。模型评估程序通常评估模型恢复样本协方差关系的能力。在估计这些模型的贝叶斯方法中，采用了一种略有不同（约束较少）的方法，该方法侧重于观察到的数据，而不是派生的汇总统计数据。

接下来我们将绘制配对图以可视化相关性的性质

ax = sns.pairplot(df[drivers], kind="reg", corner=True, diag_kind="kde")
plt.suptitle("Pair Plot of Indicator Metrics with Regression Fits", fontsize=30);
../_images/db0ad3e27df5db905e86df53ed194c146901e3b038ea44237681fc0471c9d1a2.png

我们试图在我们的CFA模型中提炼出这种广泛的关系。我们如何能够将这种复杂的联合分布结构化，使其既合理又可解释？

测量模型#

测量模型是更广泛的结构方程模型中的一个关键组成部分。测量模型规定了观测变量（通常是调查项目或指标）与其潜在构念（通常称为因子或潜在变量）之间的关系。我们通过关注一种具有自身历史的测量模型——验证性因子模型（CFA）来开始我们对SEM模型的一般介绍，该模型规定了我们的指标变量与潜在因子之间的特定结构关系。正是这种结构在我们的建模中需要得到验证。

我们将首先在PyMC中拟合一个“简单”的CFA模型，以展示各个部分如何组合在一起，然后我们将扩展我们的关注点。在这里，我们忽略了大部分的指示变量，并专注于以下两个潜在构念的概念：(1) 社交自我效能和(2) 生活满意度。

我们的目标是阐述一个数学结构，其中我们的指示变量 \(x_{ij}\) 由潜在因子 \(\text{Ksi}_{j}\) 通过估计的因子载荷 \(\lambda_{ij}\) 决定。从功能上讲，我们有一组带有误差项 \(\psi_i\) 的方程，用于每个个体。

\[\begin{split} x_{1} = \tau_{1} + \lambda_{11}\text{Ksi}_{1} + \psi_{1} \\ x_{2} = \tau_{2} + \lambda_{21}\text{Ksi}_{1} + \psi_{2} \\ ... \\ x_{n} = \tau_{n} + \lambda_{n2}\text{Ksi}_{2} + \psi_{n} \end{split}\]

或更简洁地

\[ \mathbf{x} = \tau + \Lambda\text{Ksi} + \Psi \]

目标是在这些潜在项的协方差方面阐述不同因素之间的关系，并估计每个潜在因素与显性指标变量之间的关系。从高层次来看，我们可以说观测数据的联合分布可以通过以下模式的条件化来表示。

\[p(\mathbf{x_{i}}^{T}.....\mathbf{x_{q}}^{T} | \text{Ksi}, \Psi, \tau, \Lambda) \sim Normal(\tau + \Lambda\cdot \text{Ksi}, \Psi) \]

我们提出一个论点，即来自每个个体 \(q\) 的多变量观测值 \(\mathbf{x}\) 可以被认为是条件可交换的，并且通过德菲内蒂定理的贝叶斯条件化来表示。这是用于估计CFA和SEM模型的贝叶斯方法。我们正在寻求一种条件化结构，该结构可以根据潜在构念和构念与观测数据点之间的假设关系来反向预测观测数据。我们将在下面展示如何将这些结构构建到我们的模型中

# Set up coordinates for appropriate indexing of latent factors
coords = {
    "obs": list(range(len(df))),
    "indicators": ["se_social_p1", "se_social_p2", "se_social_p3", "ls_p1", "ls_p2", "ls_p3"],
    "indicators_1": ["se_social_p1", "se_social_p2", "se_social_p3"],
    "indicators_2": ["ls_p1", "ls_p2", "ls_p3"],
    "latent": ["SE_SOC", "LS"],
}


obs_idx = list(range(len(df)))
with pm.Model(coords=coords) as model:

    # Set up Factor Loadings
    lambdas_ = pm.Normal("lambdas_1", 1, 10, dims=("indicators_1"))
    # Force a fixed scale on the factor loadings for factor 1
    lambdas_1 = pm.Deterministic(
        "lambdas1", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_1")
    )
    lambdas_ = pm.Normal("lambdas_2", 1, 10, dims=("indicators_2"))
    # Force a fixed scale on the factor loadings for factor 2
    lambdas_2 = pm.Deterministic(
        "lambdas2", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_2")
    )

    # Specify covariance structure between latent factors
    kappa = 0
    sd_dist = pm.Exponential.dist(1.0, shape=2)
    chol, _, _ = pm.LKJCholeskyCov("chol_cov", n=2, eta=2, sd_dist=sd_dist, compute_corr=True)
    ksi = pm.MvNormal("ksi", kappa, chol=chol, dims=("obs", "latent"))

    # Construct Pseudo Observation matrix based on Factor Loadings
    tau = pm.Normal("tau", 3, 10, dims="indicators")
    m1 = tau[0] + ksi[obs_idx, 0] * lambdas_1[0]
    m2 = tau[1] + ksi[obs_idx, 0] * lambdas_1[1]
    m3 = tau[2] + ksi[obs_idx, 0] * lambdas_1[2]
    m4 = tau[3] + ksi[obs_idx, 1] * lambdas_2[0]
    m5 = tau[4] + ksi[obs_idx, 1] * lambdas_2[1]
    m6 = tau[5] + ksi[obs_idx, 1] * lambdas_2[2]

    mu = pm.Deterministic("mu", pm.math.stack([m1, m2, m3, m4, m5, m6]).T)

    ## Error Terms
    Psi = pm.InverseGamma("Psi", 5, 10, dims="indicators")

    # Likelihood
    _ = pm.Normal(
        "likelihood",
        mu,
        Psi,
        observed=df[
            ["se_social_p1", "se_social_p2", "se_social_p3", "ls_p1", "ls_p2", "ls_p3"]
        ].values,
    )

    idata = pm.sample(
        nuts_sampler="numpyro", target_accept=0.95, idata_kwargs={"log_likelihood": True}
    )
    idata.extend(pm.sample_posterior_predictive(idata))

pm.model_to_graphviz(model)

Compiling...
Compilation time = 0:00:02.037172
Sampling...

Sampling time = 0:00:04.970539
Transforming variables...
Transformation time = 0:00:00.366997
Computing Log Likelihood...
Log Likelihood time = 0:00:00.248048
Sampling: [likelihood]
100.00% [4000/4000 00:00<00:00]
../_images/d3ad7e3d79ec922c8a3296117f1b37f732dad72205a68377df84b4d73bd7b3a2.svg

这里，模型结构和依赖图变得更加清晰。我们的似然项模型是一个283x6观测值的结果矩阵，即6个问题的调查响应。这些调查响应被建模为来自多元正态分布\(Ksi\)的回归类结果，具有潜在结构之间的先验相关性。然后，我们指定每个结果测量如何是潜在因子之一的函数，由适当的因子载荷lambda修改。

测量模型结构#

我们现在可以看到，潜在构念之间的协方差结构是整体模型设计中的一个重要部分，它被前馈到我们的伪回归组件中，并根据各自的lambda项进行加权。

az.summary(idata, var_names=["lambdas1", "lambdas2"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
lambdas1[se_social_p1] 1.000 0.000 1.000 1.000 0.000 0.000 4000.0 4000.0 NaN
lambdas1[se_social_p2] 0.977 0.060 0.863 1.089 0.002 0.001 993.0 1688.0 1.0
lambdas1[se_social_p3] 0.947 0.074 0.810 1.091 0.002 0.002 1110.0 1965.0 1.0
lambdas2[ls_p1] 1.000 0.000 1.000 1.000 0.000 0.000 4000.0 4000.0 NaN
lambdas2[ls_p2] 0.815 0.087 0.672 0.989 0.004 0.003 524.0 792.0 1.0
lambdas2[ls_p3] 0.861 0.095 0.689 1.047 0.004 0.003 713.0 1164.0 1.0

这些因子载荷通常在解释结构效度时非常重要。因为我们已经指定其中一个指示变量固定为1，其他加载在该因子上的指示变量应该具有与定义结构尺度的固定点指示变量大致相同的载荷系数。我们寻找载荷之间的一致性，以评估这些指示变量是否是结构的可靠测量，即如果指示变量的载荷偏离单位1太远，那么就有理由认为这些指示变量不属于同一个因子结构。

idata
arviz.InferenceData
    • <xarray.Dataset>
Dimensions:              (chain: 4, draw: 1000, indicators_1: 3,
                          indicators_2: 3, obs: 283, latent: 2, indicators: 6,
                          chol_cov_dim_0: 3, chol_cov_corr_dim_0: 2,
                          chol_cov_corr_dim_1: 2, chol_cov_stds_dim_0: 2,
                          mu_dim_0: 283, mu_dim_1: 6)
Coordinates: (12/13)
  * chain                (chain) int64 0 1 2 3
  * draw                 (draw) int64 0 1 2 3 4 5 6 ... 994 995 996 997 998 999
  * indicators_1         (indicators_1) <U12 'se_social_p1' ... 'se_social_p3'
  * indicators_2         (indicators_2) <U5 'ls_p1' 'ls_p2' 'ls_p3'
  * obs                  (obs) int64 0 1 2 3 4 5 6 ... 277 278 279 280 281 282
  * latent               (latent) <U6 'SE_SOC' 'LS'
    ...                   ...
  * chol_cov_dim_0       (chol_cov_dim_0) int64 0 1 2
  * chol_cov_corr_dim_0  (chol_cov_corr_dim_0) int64 0 1
  * chol_cov_corr_dim_1  (chol_cov_corr_dim_1) int64 0 1
  * chol_cov_stds_dim_0  (chol_cov_stds_dim_0) int64 0 1
  * mu_dim_0             (mu_dim_0) int64 0 1 2 3 4 5 ... 278 279 280 281 282
  * mu_dim_1             (mu_dim_1) int64 0 1 2 3 4 5
Data variables:
    lambdas_1            (chain, draw, indicators_1) float64 -1.601 ... 0.962
    lambdas_2            (chain, draw, indicators_2) float64 11.47 ... 0.7527
    ksi                  (chain, draw, obs, latent) float64 0.4271 ... 0.9507
    tau                  (chain, draw, indicators) float64 5.301 5.437 ... 5.233
    chol_cov             (chain, draw, chol_cov_dim_0) float64 0.6359 ... 0.5823
    Psi                  (chain, draw, indicators) float64 0.4654 ... 0.6677
    lambdas1             (chain, draw, indicators_1) float64 1.0 ... 0.962
    lambdas2             (chain, draw, indicators_2) float64 1.0 ... 0.7527
    chol_cov_corr        (chain, draw, chol_cov_corr_dim_0, chol_cov_corr_dim_1) float64 ...
    chol_cov_stds        (chain, draw, chol_cov_stds_dim_0) float64 0.6359 .....
    mu                   (chain, draw, mu_dim_0, mu_dim_1) float64 5.728 ... ...
Attributes:
    created_at:     2024-09-25T11:16:42.786789
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:           (chain: 4, draw: 1000, likelihood_dim_2: 283,
                       likelihood_dim_3: 6)
Coordinates:
  * chain             (chain) int64 0 1 2 3
  * draw              (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
  * likelihood_dim_2  (likelihood_dim_2) int64 0 1 2 3 4 ... 278 279 280 281 282
  * likelihood_dim_3  (likelihood_dim_3) int64 0 1 2 3 4 5
Data variables:
    likelihood        (chain, draw, likelihood_dim_2, likelihood_dim_3) float64 ...
Attributes:
    created_at:                 2024-09-25T11:16:43.032825
    arviz_version:              0.17.0
    inference_library:          pymc
    inference_library_version:  5.10.3

    • <xarray.Dataset>
Dimensions:           (chain: 4, draw: 1000, likelihood_dim_0: 283,
                       likelihood_dim_1: 6)
Coordinates:
  * chain             (chain) int64 0 1 2 3
  * draw              (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
  * likelihood_dim_0  (likelihood_dim_0) int64 0 1 2 3 4 ... 278 279 280 281 282
  * likelihood_dim_1  (likelihood_dim_1) int64 0 1 2 3 4 5
Data variables:
    likelihood        (chain, draw, likelihood_dim_0, likelihood_dim_1) float64 ...
Attributes:
    created_at:     2024-09-25T11:16:42.790979
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:          (chain: 4, draw: 1000)
Coordinates:
  * chain            (chain) int64 0 1 2 3
  * draw             (draw) int64 0 1 2 3 4 5 6 ... 993 994 995 996 997 998 999
Data variables:
    acceptance_rate  (chain, draw) float64 0.9026 0.9604 0.9726 ... 0.992 0.9294
    step_size        (chain, draw) float64 0.1464 0.1464 ... 0.1427 0.1427
    diverging        (chain, draw) bool False False False ... False False False
    energy           (chain, draw) float64 2.091e+03 2.111e+03 ... 2.072e+03
    n_steps          (chain, draw) int64 31 31 31 31 31 31 ... 31 31 31 31 31 31
    tree_depth       (chain, draw) int64 5 5 5 5 5 5 5 5 5 ... 5 5 5 5 5 5 5 5 5
    lp               (chain, draw) float64 1.803e+03 1.804e+03 ... 1.78e+03
Attributes:
    created_at:     2024-09-25T11:16:42.789976
    arviz_version:  0.17.0

    • <xarray.Dataset>
Dimensions:           (likelihood_dim_0: 283, likelihood_dim_1: 6)
Coordinates:
  * likelihood_dim_0  (likelihood_dim_0) int64 0 1 2 3 4 ... 278 279 280 281 282
  * likelihood_dim_1  (likelihood_dim_1) int64 0 1 2 3 4 5
Data variables:
    likelihood        (likelihood_dim_0, likelihood_dim_1) float64 5.8 ... 5.75
Attributes:
    created_at:                 2024-09-25T11:16:42.791317
    arviz_version:              0.17.0
    inference_library:          numpyro
    inference_library_version:  0.13.2
    sampling_time:              4.970539

让我们绘制轨迹诊断图，以验证采样器是否已很好地收敛到后验分布。

az.plot_trace(idata, var_names=["lambdas1", "lambdas2", "tau", "Psi", "ksi"]);
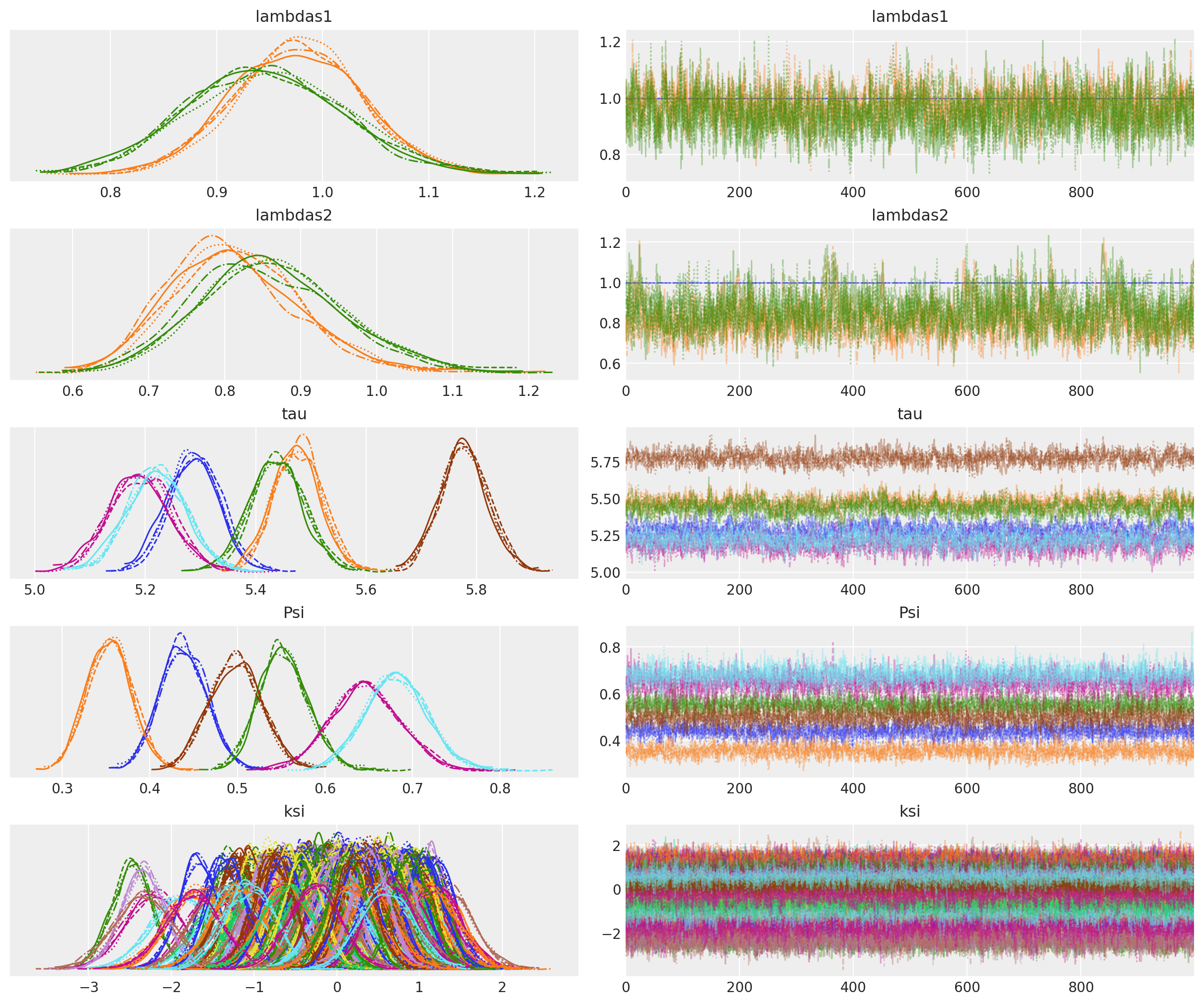
../_images/dbff0c1df09f2a3e3f747707272f557c8544f9687b5650b06bcb8fd66f1f7a3a.png

采样潜在结构#

关于贝叶斯方法拟合CFA和SEM模型的一个特别值得强调的方面是，我们现在可以访问潜在变量的后验分布。这些样本可以为我们调查中的特定个体提供见解，而这些见解在显变量的多元展示中更难以获得。

Hide code cell source 
fig, axs = plt.subplots(1, 2, figsize=(20, 9))
axs = axs.flatten()
ax1 = axs[0]
ax2 = axs[1]
az.plot_forest(
    idata,
    var_names=["ksi"],
    combined=True,
    ax=ax1,
    colors="forestgreen",
    coords={"latent": ["SE_SOC"]},
)
az.plot_forest(
    idata, var_names=["ksi"], combined=True, ax=ax2, colors="slateblue", coords={"latent": ["LS"]}
)
ax1.set_yticklabels([])
ax1.set_xlabel("SE_SOCIAL")
ax2.set_yticklabels([])
ax2.set_xlabel("LS")
ax1.axvline(-2, color="red")
ax2.axvline(-2, color="red")
ax1.set_title("Individual Social Self Efficacy \n On Latent Factor SE_SOCIAL")
ax2.set_title("Individual Life Satisfaction Metric \n On Latent Factor LS")
plt.show();
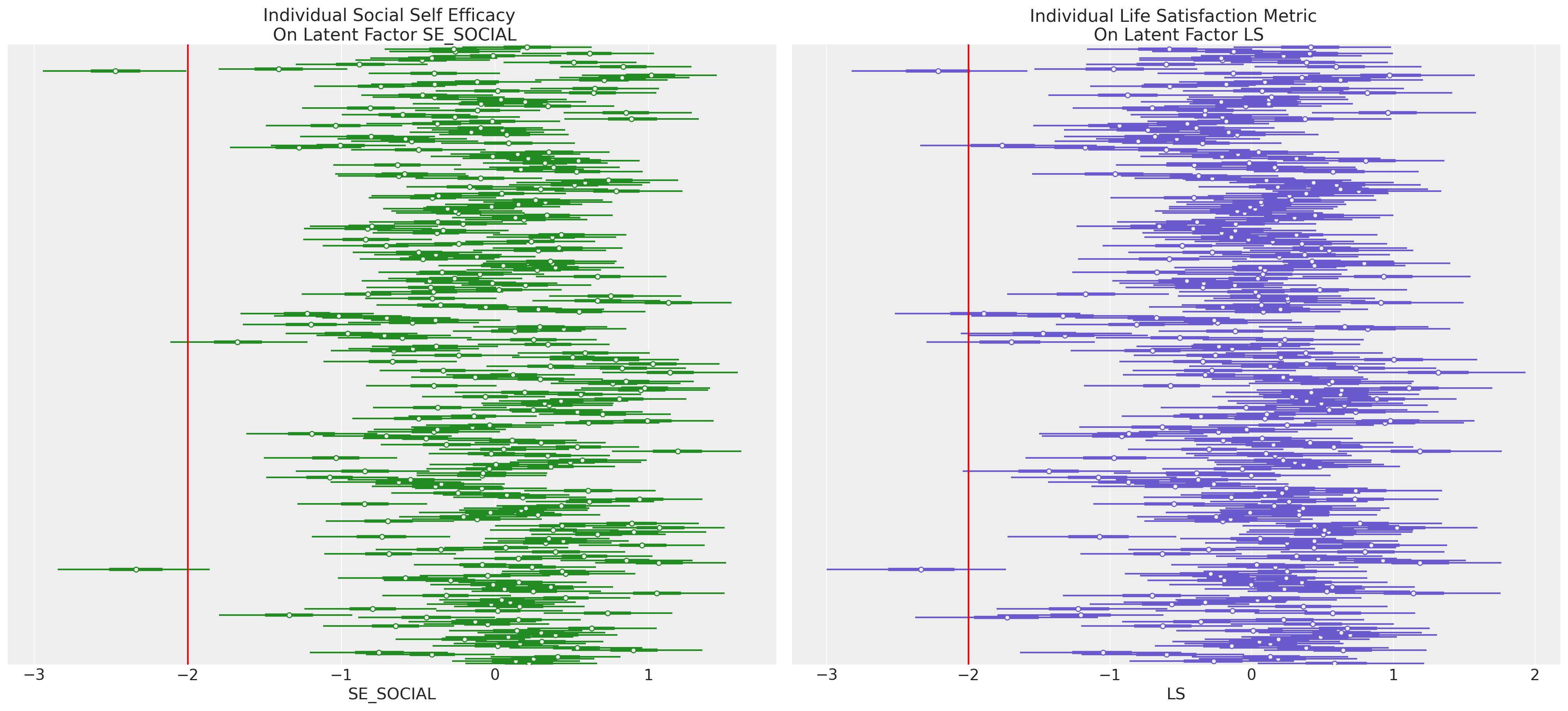
../_images/8b3d1f351b1472689ac7bd1eb3eb74dd239c817398f73bdadc92615ab9a9780f.png

通过这种方式，我们可以识别并聚焦于在一个或多个潜在构念上表现出异常的个体。

后验预测检查#

与更传统的贝叶斯建模一样，模型评估的核心组成部分是评估后验预测分布，即隐含的结果分布。在这里，我们也可以针对每个指标变量提取样本，以评估其一致性和充分性。

def make_ppc(
    idata,
    samples=100,
    drivers=["se_social_p1", "se_social_p2", "se_social_p3", "ls_p1", "ls_p2", "ls_p3"],
    dims=(2, 3),
):
    fig, axs = plt.subplots(dims[0], dims[1], figsize=(20, 10))
    axs = axs.flatten()
    for i in range(len(drivers)):
        for j in range(samples):
            temp = az.extract(idata["posterior_predictive"].sel({"likelihood_dim_3": i}))[
                "likelihood"
            ].values[:, j]
            temp = pd.DataFrame(temp, columns=["likelihood"])
            if j == 0:
                axs[i].hist(df[drivers[i]], alpha=0.3, ec="black", bins=20, label="Observed Scores")
                axs[i].hist(
                    temp["likelihood"], color="purple", alpha=0.1, bins=20, label="Predicted Scores"
                )
            else:
                axs[i].hist(df[drivers[i]], alpha=0.3, ec="black", bins=20)
                axs[i].hist(temp["likelihood"], color="purple", alpha=0.1, bins=20)
            axs[i].set_title(f"Posterior Predictive Checks {drivers[i]}")
            axs[i].legend()
    plt.tight_layout()
    plt.show()


make_ppc(idata)
del idata
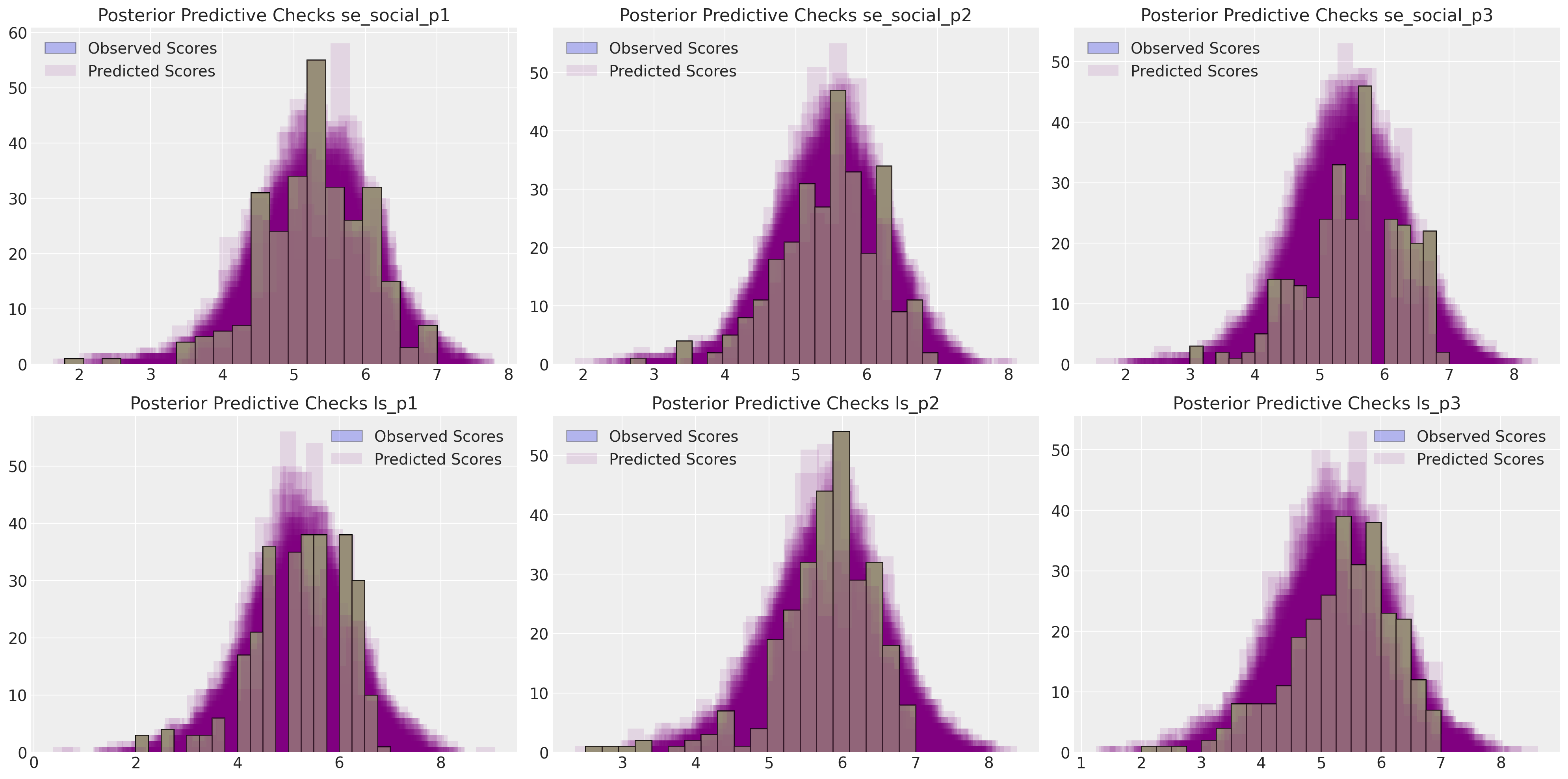
../_images/d55c362796fffa145ccc878d3b3804c742435c5536e4c9dd2093e6550b125461.png

这显示了对观测数据的相对良好的恢复。

中间交叉加载模型#

当我们只看到拟合良好的模型时，测量模型的概念可能有点晦涩。相反，我们想简要展示一个不合适的测量模型如何反映在因子载荷的估计参数中。这里我们指定一个测量模型，试图将se_social和sup_parents指标耦合在一起，并将它们捆绑到同一个因子中。

coords = {
    "obs": list(range(len(df))),
    "indicators": [
        "se_social_p1",
        "se_social_p2",
        "se_social_p3",
        "sup_parents_p1",
        "sup_parents_p2",
        "sup_parents_p3",
        "ls_p1",
        "ls_p2",
        "ls_p3",
    ],
    ## Attempt Cross-Loading of two metric types on one factor
    "indicators_1": [
        "se_social_p1",
        "se_social_p2",
        "se_social_p3",
        "sup_parents_p1",
        "sup_parents_p2",
        "sup_parents_p3",
    ],
    "indicators_2": ["ls_p1", "ls_p2", "ls_p3"],
    "latent": ["SE_SOC", "LS"],
}


obs_idx = list(range(len(df)))
with pm.Model(coords=coords) as model:

    Psi = pm.InverseGamma("Psi", 5, 10, dims="indicators")
    lambdas_ = pm.Normal("lambdas_1", 1, 10, dims=("indicators_1"))
    # Force a fixed scale on the factor loadings for factor 1
    lambdas_1 = pm.Deterministic(
        "lambdas1", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_1")
    )
    lambdas_ = pm.Normal("lambdas_2", 1, 10, dims=("indicators_2"))
    # Force a fixed scale on the factor loadings for factor 2
    lambdas_2 = pm.Deterministic(
        "lambdas2", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_2")
    )
    tau = pm.Normal("tau", 3, 10, dims="indicators")
    # Specify covariance structure between latent factors
    kappa = 0
    sd_dist = pm.Exponential.dist(1.0, shape=2)
    chol, _, _ = pm.LKJCholeskyCov("chol_cov", n=2, eta=2, sd_dist=sd_dist, compute_corr=True)
    ksi = pm.MvNormal("ksi", kappa, chol=chol, dims=("obs", "latent"))

    # Construct Observation matrix
    m1 = tau[0] + ksi[obs_idx, 0] * lambdas_1[0]
    m2 = tau[1] + ksi[obs_idx, 0] * lambdas_1[1]
    m3 = tau[2] + ksi[obs_idx, 0] * lambdas_1[2]
    m4 = tau[3] + ksi[obs_idx, 0] * lambdas_1[3]
    m5 = tau[4] + ksi[obs_idx, 0] * lambdas_1[4]
    m6 = tau[5] + ksi[obs_idx, 0] * lambdas_1[5]
    m7 = tau[3] + ksi[obs_idx, 1] * lambdas_2[0]
    m8 = tau[4] + ksi[obs_idx, 1] * lambdas_2[1]
    m9 = tau[5] + ksi[obs_idx, 1] * lambdas_2[2]

    mu = pm.Deterministic("mu", pm.math.stack([m1, m2, m3, m4, m5, m6, m7, m8, m9]).T)
    _ = pm.Normal(
        "likelihood",
        mu,
        Psi,
        observed=df[
            [
                "se_social_p1",
                "se_social_p2",
                "se_social_p3",
                "sup_parents_p1",
                "sup_parents_p2",
                "sup_parents_p3",
                "ls_p1",
                "ls_p2",
                "ls_p3",
            ]
        ].values,
    )

    idata = pm.sample(
        # draws = 4000,
        draws=10000,
        nuts_sampler="numpyro",
        target_accept=0.99,
        idata_kwargs={"log_likelihood": True},
        random_seed=114,
    )
    idata.extend(pm.sample_posterior_predictive(idata))

Compiling...
Compilation time = 0:00:01.765569
Sampling...

Sampling time = 0:00:26.201814
Transforming variables...
Transformation time = 0:00:01.184088
Computing Log Likelihood...
Log Likelihood time = 0:00:00.831334
Sampling: [likelihood]
100.00% [40000/40000 00:02<00:00]

再次，我们的模型采样良好，但参数估计表明，在我们试图强制两者度量集的尺度之间存在一些不一致性。

az.summary(idata, var_names=["lambdas1", "lambdas2"])
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
lambdas1[se_social_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas1[se_social_p2] 0.928 0.128 0.694 1.172 0.002 0.002 3090.0 5423.0 1.0
lambdas1[se_social_p3] 0.854 0.139 0.598 1.121 0.002 0.002 4600.0 8366.0 1.0
lambdas1[sup_parents_p1] 2.321 0.289 1.807 2.867 0.008 0.005 1421.0 2736.0 1.0
lambdas1[sup_parents_p2] 2.171 0.278 1.684 2.699 0.008 0.005 1333.0 2592.0 1.0
lambdas1[sup_parents_p3] 2.334 0.290 1.832 2.898 0.008 0.005 1442.0 2795.0 1.0
lambdas2[ls_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas2[ls_p2] 0.777 0.105 0.589 0.975 0.002 0.002 2530.0 4296.0 1.0
lambdas2[ls_p3] 1.080 0.135 0.840 1.335 0.003 0.002 2271.0 3902.0 1.0

这在诊断能量图中也同样得到了体现。

fig, axs = plt.subplots(1, 2, figsize=(20, 9))
axs = axs.flatten()
az.plot_energy(idata, ax=axs[0])
az.plot_forest(idata, var_names=["lambdas1"], combined=True, ax=axs[1]);
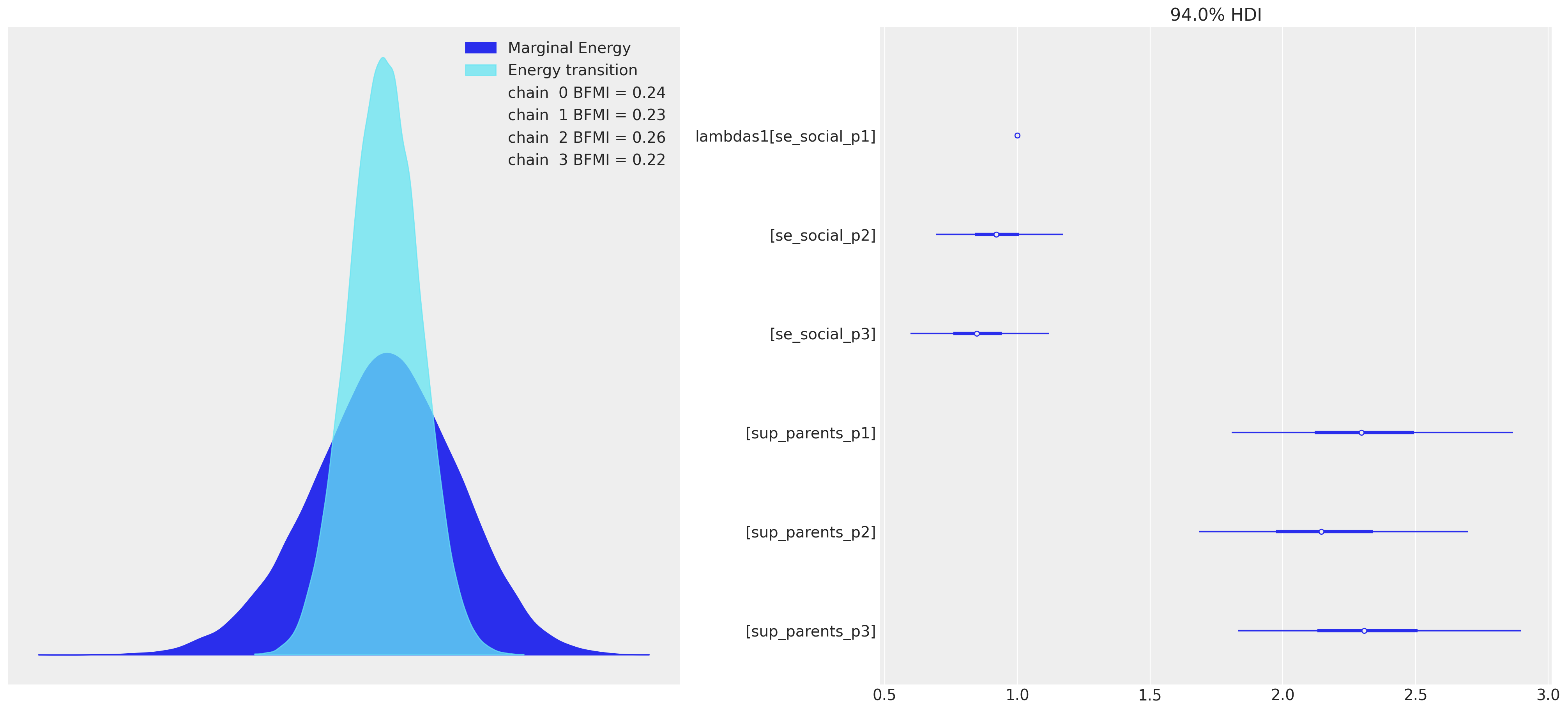
../_images/3282e96422c80ef6af337df47a394ff972975abc0e4f6f47f7089a9f5539f135.png

这暗示了各种测量模型设定错误，并应迫使我们回到绘图板。一个适当的测量模型将指示变量映射到一个一致定义的潜在构念，该构念合理地反映了实现指示指标的各个方面。

完整测量模型#

考虑到这一点，我们现在将指定一个完整的测量，将每个主题相似的指标映射到单个潜在构念。这要求我们假设5个不同的构念，其中每个构念只允许三个指标加载。选择哪个指标加载在潜在构念上，在我们的情况下是由每个测量所要测量的构念决定的。在典型的 lavaan 语法中，我们可能会将模型写成如下：

SUP_Parents =~ sup_parents_p1 + sup_parents_p2 + sup_parents_p3
SUP_Friends =~ sup_friends_p1 + sup_friends_p2 + sup_friends_p3
SE_Academic =~ se_acad_p1 + se_acad_p2 + se_acad_p3
SE_Social =~ se_social_p1 + se_social_p2 + se_social_p3
LS  =~ ls_p1 + ls_p2 + ls_p3

其中=~语法表示“由...衡量”的关系。在这种类型的测量模型拟合中，我们试图估计的是每个这些指标变量是如何由潜在构念决定的。

drivers = [
    "se_acad_p1",
    "se_acad_p2",
    "se_acad_p3",
    "se_social_p1",
    "se_social_p2",
    "se_social_p3",
    "sup_friends_p1",
    "sup_friends_p2",
    "sup_friends_p3",
    "sup_parents_p1",
    "sup_parents_p2",
    "sup_parents_p3",
    "ls_p1",
    "ls_p2",
    "ls_p3",
]

coords = {
    "obs": list(range(len(df))),
    "indicators": drivers,
    "indicators_1": ["se_acad_p1", "se_acad_p2", "se_acad_p3"],
    "indicators_2": ["se_social_p1", "se_social_p2", "se_social_p3"],
    "indicators_3": ["sup_friends_p1", "sup_friends_p2", "sup_friends_p3"],
    "indicators_4": ["sup_parents_p1", "sup_parents_p2", "sup_parents_p3"],
    "indicators_5": ["ls_p1", "ls_p2", "ls_p3"],
    "latent": ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P", "LS"],
    "latent1": ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P", "LS"],
}

obs_idx = list(range(len(df)))
with pm.Model(coords=coords) as model:

    Psi = pm.InverseGamma("Psi", 5, 10, dims="indicators")
    lambdas_ = pm.Normal("lambdas_1", 1, 10, dims=("indicators_1"))
    lambdas_1 = pm.Deterministic(
        "lambdas1", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_1")
    )
    lambdas_ = pm.Normal("lambdas_2", 1, 10, dims=("indicators_2"))
    lambdas_2 = pm.Deterministic(
        "lambdas2", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_2")
    )
    lambdas_ = pm.Normal("lambdas_3", 1, 10, dims=("indicators_3"))
    lambdas_3 = pm.Deterministic(
        "lambdas3", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_3")
    )
    lambdas_ = pm.Normal("lambdas_4", 1, 10, dims=("indicators_4"))
    lambdas_4 = pm.Deterministic(
        "lambdas4", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_4")
    )
    lambdas_ = pm.Normal("lambdas_5", 1, 10, dims=("indicators_5"))
    lambdas_5 = pm.Deterministic(
        "lambdas5", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_5")
    )
    tau = pm.Normal("tau", 3, 10, dims="indicators")
    kappa = 0
    sd_dist = pm.Exponential.dist(1.0, shape=5)
    chol, _, _ = pm.LKJCholeskyCov("chol_cov", n=5, eta=2, sd_dist=sd_dist, compute_corr=True)
    cov = pm.Deterministic("cov", chol.dot(chol.T), dims=("latent", "latent1"))
    ksi = pm.MvNormal("ksi", kappa, chol=chol, dims=("obs", "latent"))

    m0 = tau[0] + ksi[obs_idx, 0] * lambdas_1[0]
    m1 = tau[1] + ksi[obs_idx, 0] * lambdas_1[1]
    m2 = tau[2] + ksi[obs_idx, 0] * lambdas_1[2]
    m3 = tau[3] + ksi[obs_idx, 1] * lambdas_2[0]
    m4 = tau[4] + ksi[obs_idx, 1] * lambdas_2[1]
    m5 = tau[5] + ksi[obs_idx, 1] * lambdas_2[2]
    m6 = tau[6] + ksi[obs_idx, 2] * lambdas_3[0]
    m7 = tau[7] + ksi[obs_idx, 2] * lambdas_3[1]
    m8 = tau[8] + ksi[obs_idx, 2] * lambdas_3[2]
    m9 = tau[9] + ksi[obs_idx, 3] * lambdas_4[0]
    m10 = tau[10] + ksi[obs_idx, 3] * lambdas_4[1]
    m11 = tau[11] + ksi[obs_idx, 3] * lambdas_4[2]
    m12 = tau[12] + ksi[obs_idx, 4] * lambdas_5[0]
    m13 = tau[13] + ksi[obs_idx, 4] * lambdas_5[1]
    m14 = tau[14] + ksi[obs_idx, 4] * lambdas_5[2]

    mu = pm.Deterministic(
        "mu", pm.math.stack([m0, m1, m2, m3, m4, m5, m6, m7, m8, m9, m10, m11, m12, m13, m14]).T
    )
    _ = pm.Normal("likelihood", mu, Psi, observed=df[drivers].values)

    idata_mm = pm.sample(
        draws=10000,
        nuts_sampler="numpyro",
        target_accept=0.98,
        tune=1000,
        idata_kwargs={"log_likelihood": True},
        random_seed=100,
    )
    idata_mm.extend(pm.sample_posterior_predictive(idata_mm))

Compiling...
Compilation time = 0:00:02.385203
Sampling...

Sampling time = 0:04:36.313368
Transforming variables...
Transformation time = 0:00:03.402148
Computing Log Likelihood...
Log Likelihood time = 0:00:01.964164
Sampling: [likelihood]
100.00% [40000/40000 00:03<00:00]

模型评估检查#

我们可以在这里快速看到这种因子结构似乎更好地进行了采样，并保持了尺度的一致性。

fig, axs = plt.subplots(1, 2, figsize=(20, 9))
axs = axs.flatten()
az.plot_energy(idata_mm, ax=axs[0])
az.plot_forest(idata_mm, var_names=["lambdas1", "lambdas2", "lambdas3"], combined=True, ax=axs[1]);
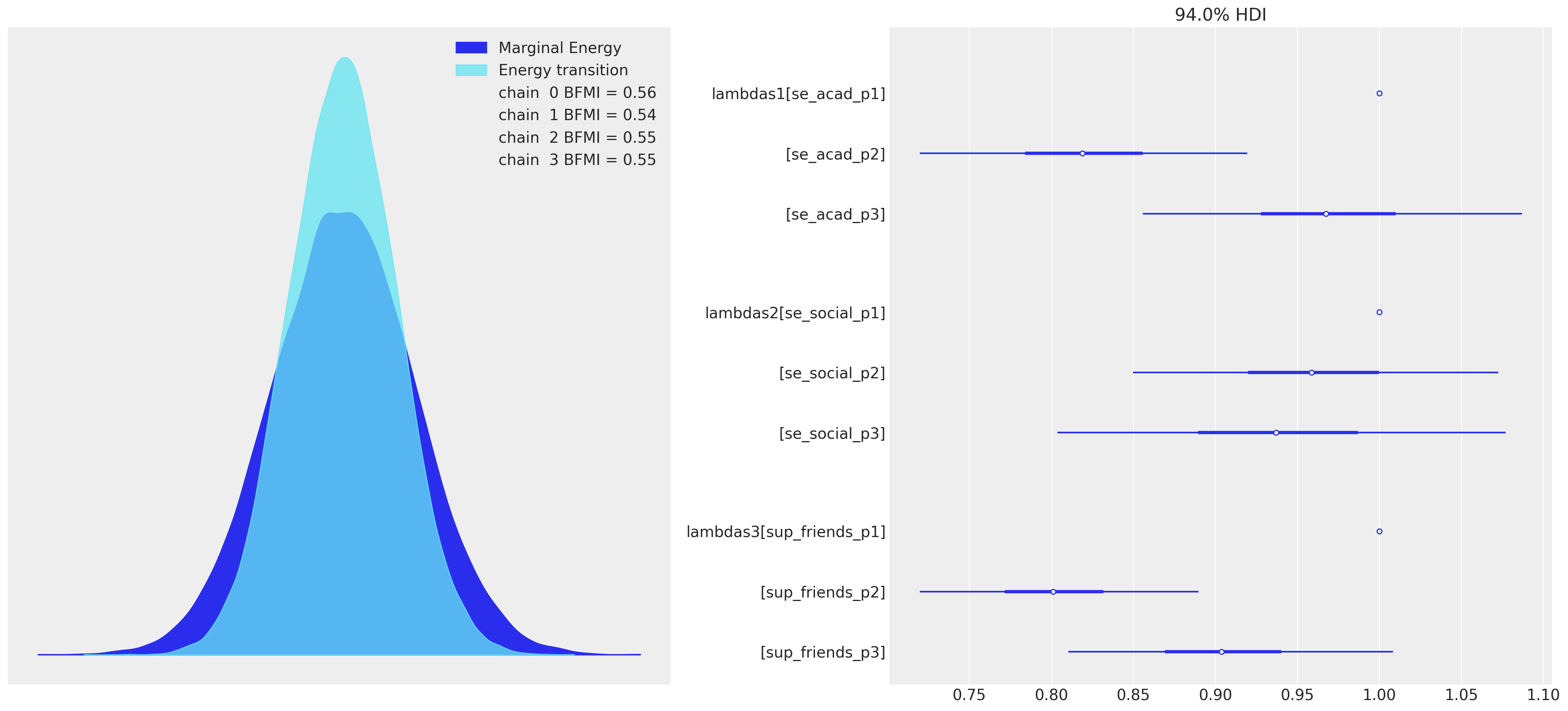
../_images/4c0e10189f28ca821f00442de44ac417512623425ca9fdcc5c1951e84d8d1d14.png

我们还可以通过评估后验预测协方差与样本协方差之间的拟合度，提取出更典型的模型评估模式。这是一个用于评估局部模型拟合统计的合理性检查。以下代码迭代后验预测分布的抽取，并在每次抽取时计算协方差或相关矩阵，我们在每次抽取时计算协方差之间的残差，然后对所有抽取进行平均。

def get_posterior_resids(idata, samples=100, metric="cov"):
    resids = []
    for i in range(100):
        if metric == "cov":
            model_cov = pd.DataFrame(
                az.extract(idata["posterior_predictive"])["likelihood"][:, :, i]
            ).cov()
            obs_cov = df[drivers].cov()
        else:
            model_cov = pd.DataFrame(
                az.extract(idata["posterior_predictive"])["likelihood"][:, :, i]
            ).corr()
            obs_cov = df[drivers].corr()
        model_cov.index = obs_cov.index
        model_cov.columns = obs_cov.columns
        residuals = model_cov - obs_cov
        resids.append(residuals.values.flatten())

    residuals_posterior = pd.DataFrame(pd.DataFrame(resids).mean().values.reshape(15, 15))
    residuals_posterior.index = obs_cov.index
    residuals_posterior.columns = obs_cov.index
    return residuals_posterior


residuals_posterior_cov = get_posterior_resids(idata_mm, 2500)
residuals_posterior_corr = get_posterior_resids(idata_mm, 2500, metric="corr")

这些表格适合用于绘制漂亮的图表，我们可以在其中突出显示与样本协方差和相关统计数据的偏差。

fig, ax = plt.subplots(figsize=(20, 10))
mask = np.triu(np.ones_like(residuals_posterior_corr, dtype=bool))
ax = sns.heatmap(residuals_posterior_corr, annot=True, cmap="bwr", mask=mask)
ax.set_title("Residuals between Model Implied and Sample Correlations", fontsize=25);
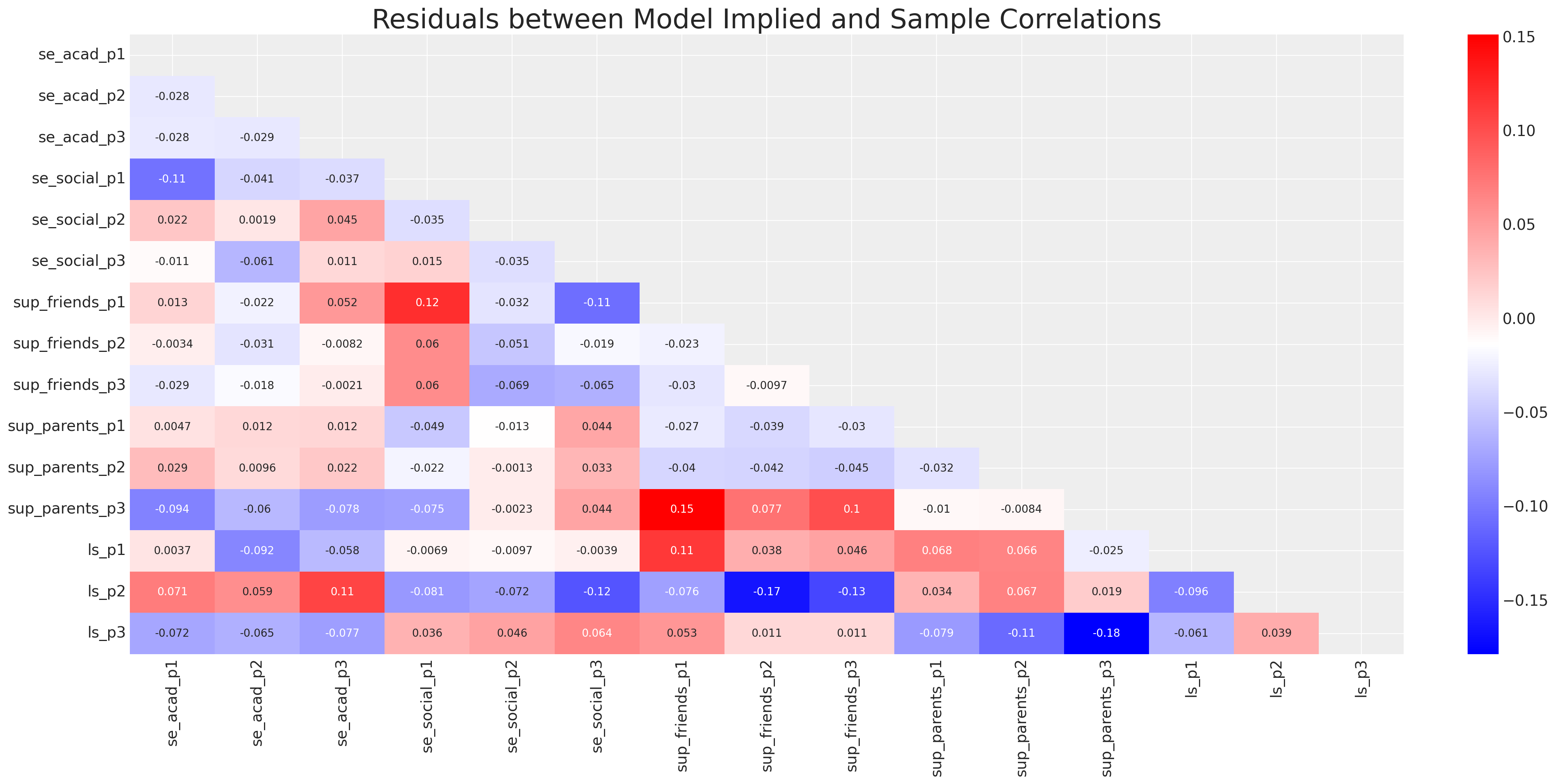
../_images/45422aad0fce25c034ab72bfc86f545ecb3b0b3e4b1caac157d3c884074a4d12.png 
fig, ax = plt.subplots(figsize=(20, 10))
ax = sns.heatmap(residuals_posterior_cov, annot=True, cmap="bwr", mask=mask)
ax.set_title("Residuals between Model Implied and Sample Covariances", fontsize=25);
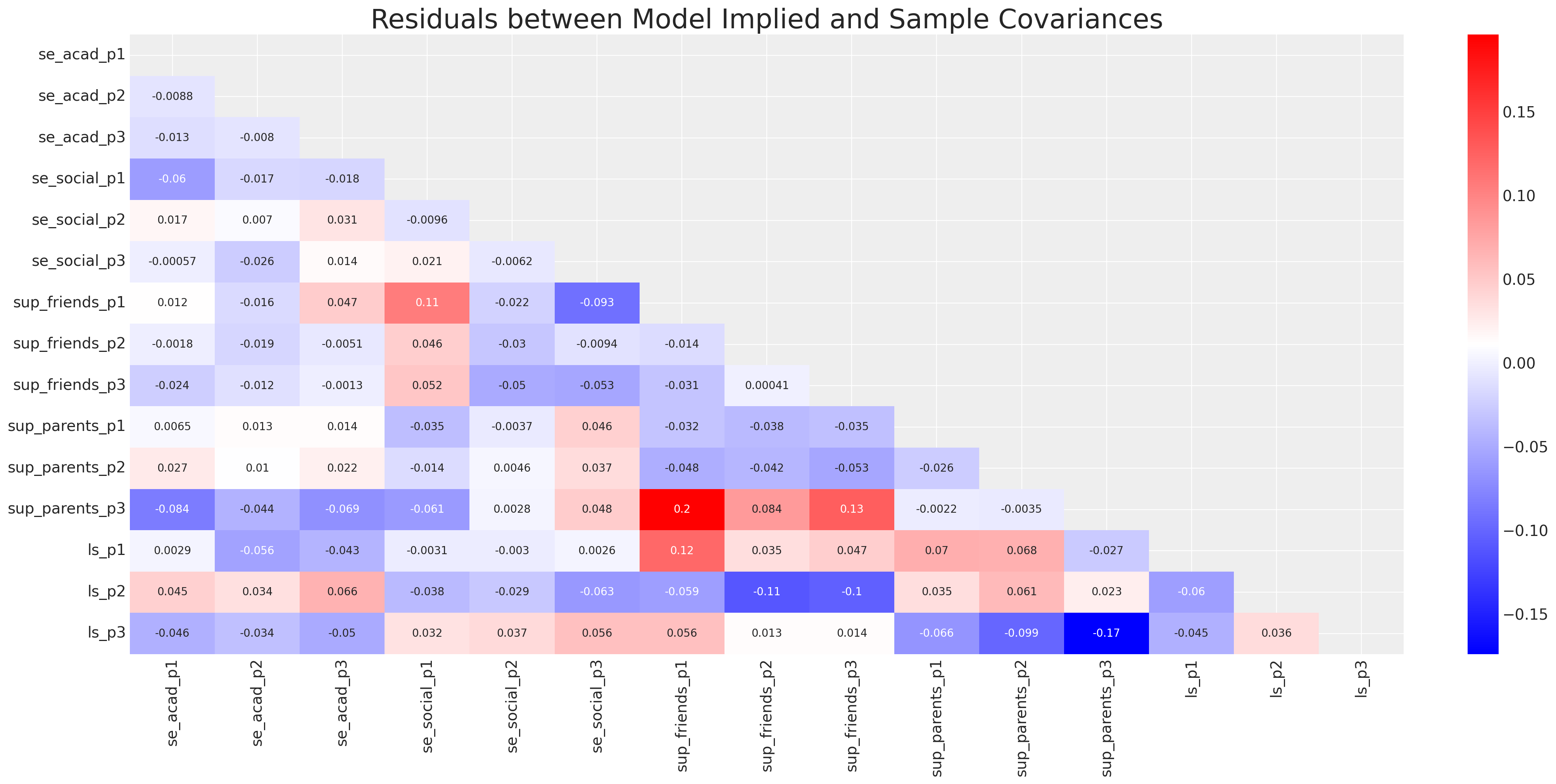
../_images/0b22af532a5b9fdcf8b521920c40a849854abf8bbc22181146ebb737609004bd.png

然而，与恢复观测数据本身相比，专注于恢复这些汇总统计数据的拟合度不那么有说服力，也更为间接。我们还可以在提取每个观测指标的预测后验分布时，进行更现代的贝叶斯后验预测检查。

make_ppc(idata_mm, 100, drivers=residuals_posterior_cov.columns, dims=(5, 3));
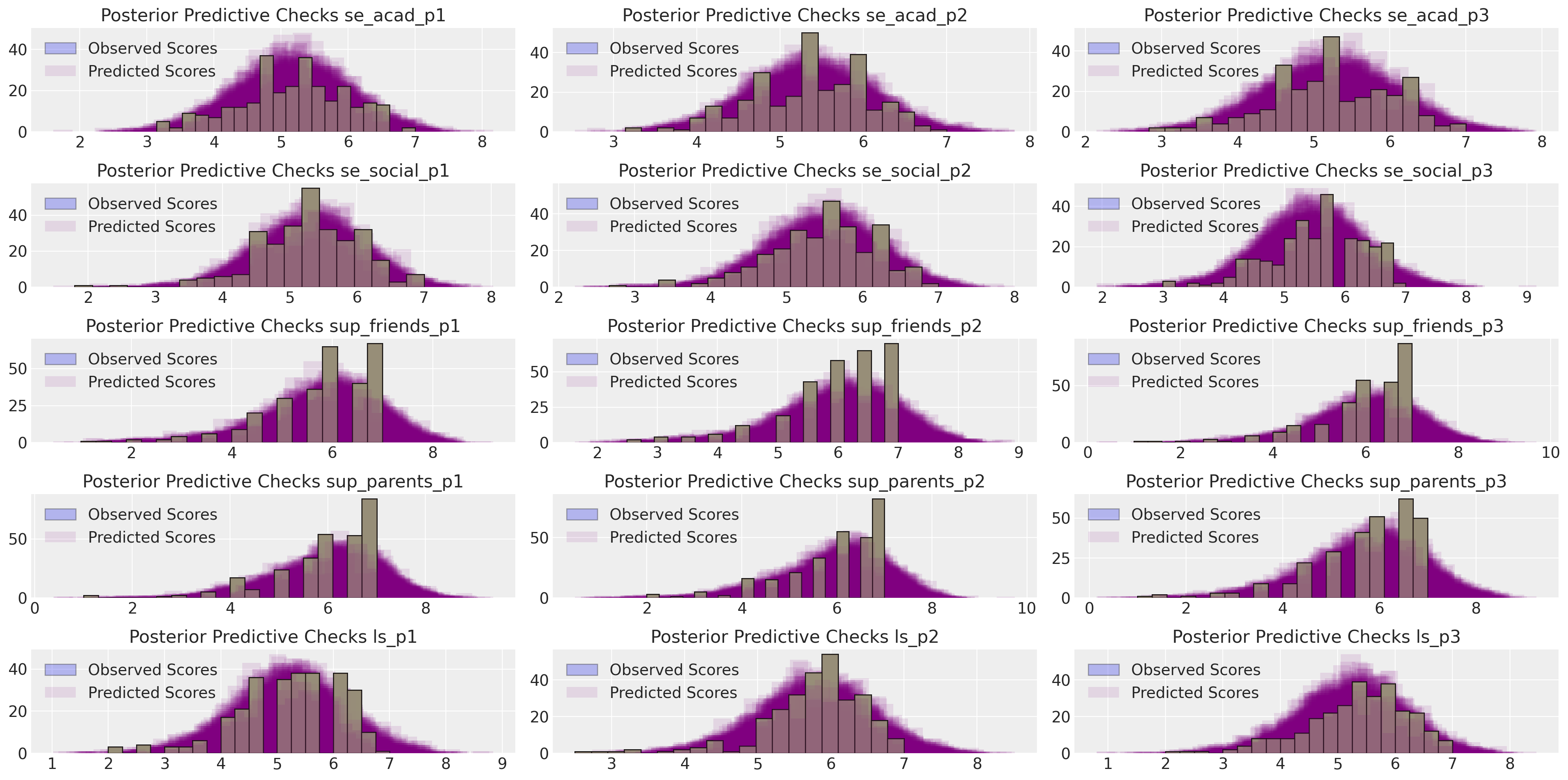
../_images/1e3d992e6ce4e14b10d7a1099a73024544d64887d231f1ef98d6ec7afb1f42bb.png

模型分析#

我们不仅对恢复观测到的数据模式感兴趣，还希望有一种方法能够提取与潜在结构相关的推论。例如，我们可以提取因子载荷，并计算该因子系统中每个指示变量以及因子本身所解释的方差量。

def make_factor_loadings_df(idata):
    factor_loadings = pd.DataFrame(
        az.summary(
            idata_mm, var_names=["lambdas1", "lambdas2", "lambdas3", "lambdas4", "lambdas5"]
        )["mean"]
    ).reset_index()
    factor_loadings["factor"] = factor_loadings["index"].str.split("[", expand=True)[0]
    factor_loadings.columns = ["factor_loading", "factor_loading_weight", "factor"]
    factor_loadings["factor_loading_weight_sq"] = factor_loadings["factor_loading_weight"] ** 2
    factor_loadings["sum_sq_loadings"] = factor_loadings.groupby("factor")[
        "factor_loading_weight_sq"
    ].transform(sum)
    factor_loadings["error_variances"] = az.summary(idata_mm, var_names=["Psi"])["mean"].values
    factor_loadings["total_indicator_variance"] = (
        factor_loadings["factor_loading_weight_sq"] + factor_loadings["error_variances"]
    )
    factor_loadings["total_variance"] = factor_loadings["total_indicator_variance"].sum()
    factor_loadings["indicator_explained_variance"] = (
        factor_loadings["factor_loading_weight_sq"] / factor_loadings["total_variance"]
    )
    factor_loadings["factor_explained_variance"] = (
        factor_loadings["sum_sq_loadings"] / factor_loadings["total_variance"]
    )
    num_cols = [c for c in factor_loadings.columns if not c in ["factor_loading", "factor"]]
    return factor_loadings


pd.set_option("display.max_colwidth", 15)
factor_loadings = make_factor_loadings_df(idata_mm)
num_cols = [c for c in factor_loadings.columns if not c in ["factor_loading", "factor"]]
factor_loadings.style.format("{:.2f}", subset=num_cols).background_gradient(
    axis=0, subset=["indicator_explained_variance", "factor_explained_variance"]
)

/var/folders/__/ng_3_9pn1f11ftyml_qr69vh0000gn/T/ipykernel_43772/1650813745.py:12: FutureWarning: The provided callable <built-in function sum> is currently using SeriesGroupBy.sum. In a future version of pandas, the provided callable will be used directly. To keep current behavior pass the string "sum" instead.
  ].transform(sum)
  factor_loading factor_loading_weight factor factor_loading_weight_sq sum_sq_loadings error_variances total_indicator_variance total_variance indicator_explained_variance factor_explained_variance
0 lambdas1[se_acad_p1] 1.00 lambdas1 1.00 2.61 0.41 1.41 21.47 0.05 0.12
1 lambdas1[se_acad_p2] 0.82 lambdas1 0.67 2.61 0.41 1.09 21.47 0.03 0.12
2 lambdas1[se_acad_p3] 0.97 lambdas1 0.94 2.61 0.47 1.41 21.47 0.04 0.12
3 lambdas2[se_social_p1] 1.00 lambdas2 1.00 2.81 0.43 1.43 21.47 0.05 0.13
4 lambdas2[se_social_p2] 0.96 lambdas2 0.92 2.81 0.36 1.29 21.47 0.04 0.13
5 lambdas2[se_social_p3] 0.94 lambdas2 0.88 2.81 0.55 1.43 21.47 0.04 0.13
6 lambdas3[sup_friends_p1] 1.00 lambdas3 1.00 2.46 0.52 1.52 21.47 0.05 0.11
7 lambdas3[sup_friends_p2] 0.80 lambdas3 0.64 2.46 0.51 1.15 21.47 0.03 0.11
8 lambdas3[sup_friends_p3] 0.91 lambdas3 0.82 2.46 0.62 1.44 21.47 0.04 0.11
9 lambdas4[sup_parents_p1] 1.00 lambdas4 1.00 3.11 0.55 1.55 21.47 0.05 0.14
10 lambdas4[sup_parents_p2] 1.04 lambdas4 1.08 3.11 0.54 1.62 21.47 0.05 0.14
11 lambdas4[sup_parents_p3] 1.01 lambdas4 1.02 3.11 0.68 1.70 21.47 0.05 0.14
12 lambdas5[ls_p1] 1.00 lambdas5 1.00 2.61 0.67 1.67 21.47 0.05 0.12
13 lambdas5[ls_p2] 0.79 lambdas5 0.63 2.61 0.53 1.16 21.47 0.03 0.12
14 lambdas5[ls_p3] 0.99 lambdas5 0.98 2.61 0.62 1.61 21.47 0.05 0.12

我们可以提取并绘制有序的权重，作为一种特征重要性图。

fig, ax = plt.subplots(figsize=(15, 8))
temp = factor_loadings[["factor_loading", "indicator_explained_variance"]].sort_values(
    by="indicator_explained_variance"
)
ax.barh(
    temp["factor_loading"], temp["indicator_explained_variance"], align="center", color="slateblue"
)
ax.set_title("Explained Variance");
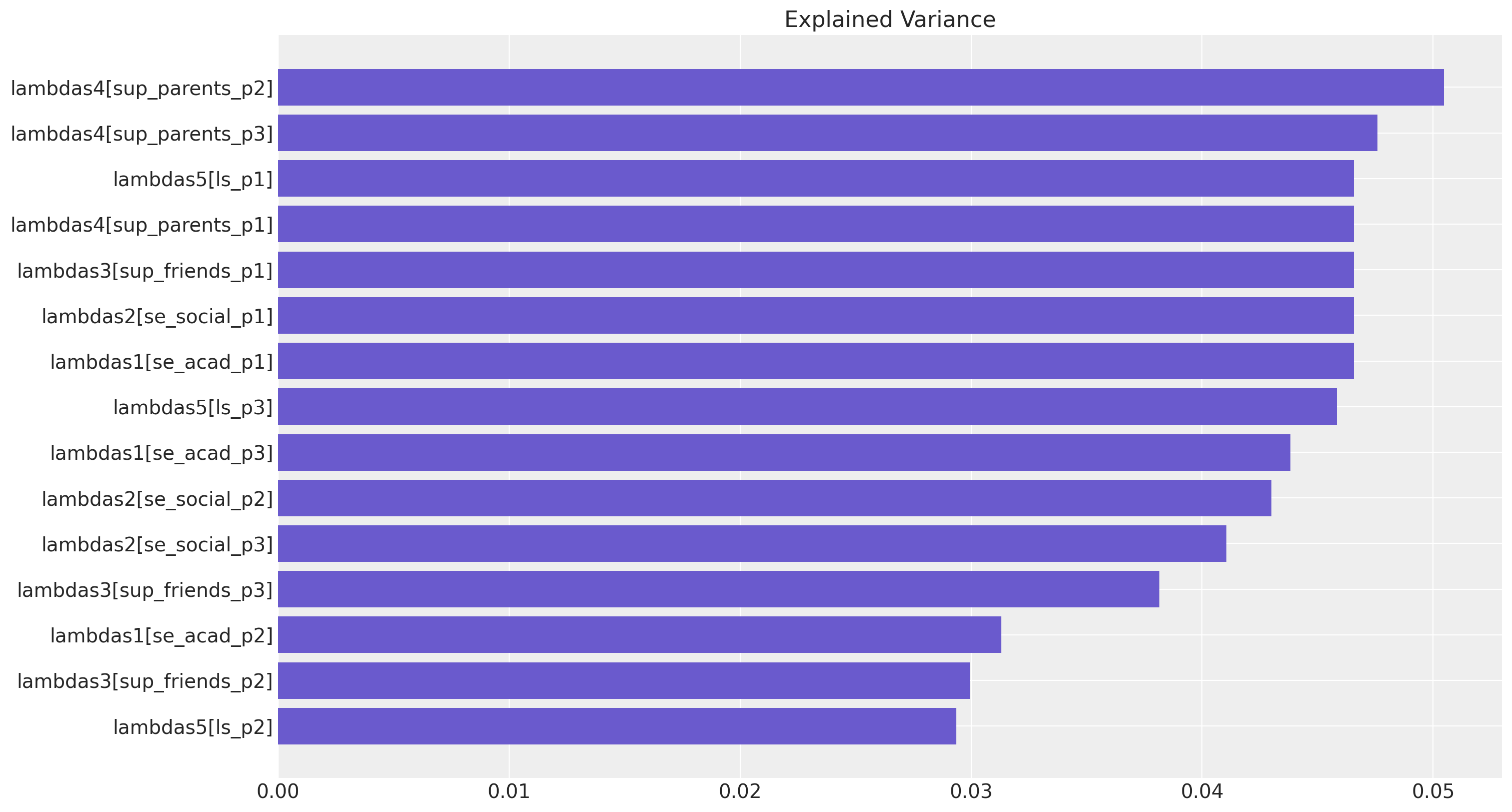
../_images/dbe8dcc773c0b6c1c167cad397d7ae115ab8eadf3820db11505d0866b5cbc803.png

这种视图的目标不一定是像在机器学习上下文中那样找到有用的特征，而是帮助理解我们系统中变化的性质。我们还可以提取潜在因素之间的协方差和相关性

Hide code cell source 
cov_df = pd.DataFrame(az.extract(idata_mm["posterior"])["cov"].mean(axis=2))
cov_df.index = ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P", "LS"]
cov_df.columns = ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P", "LS"]

correlation_df = pd.DataFrame(az.extract(idata_mm["posterior"])["chol_cov_corr"].mean(axis=2))
correlation_df.index = ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P", "LS"]
correlation_df.columns = ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P", "LS"]

fig, axs = plt.subplots(1, 2, figsize=(20, 10))
axs = axs.flatten()
mask = np.triu(np.ones_like(cov_df, dtype=bool))
sns.heatmap(cov_df, annot=True, cmap="Blues", ax=axs[0], mask=mask)
axs[0].set_title("Covariance of Latent Constructs")
axs[1].set_title("Correlation of Latent Constructs")
sns.heatmap(correlation_df, annot=True, cmap="Blues", ax=axs[1], mask=mask);
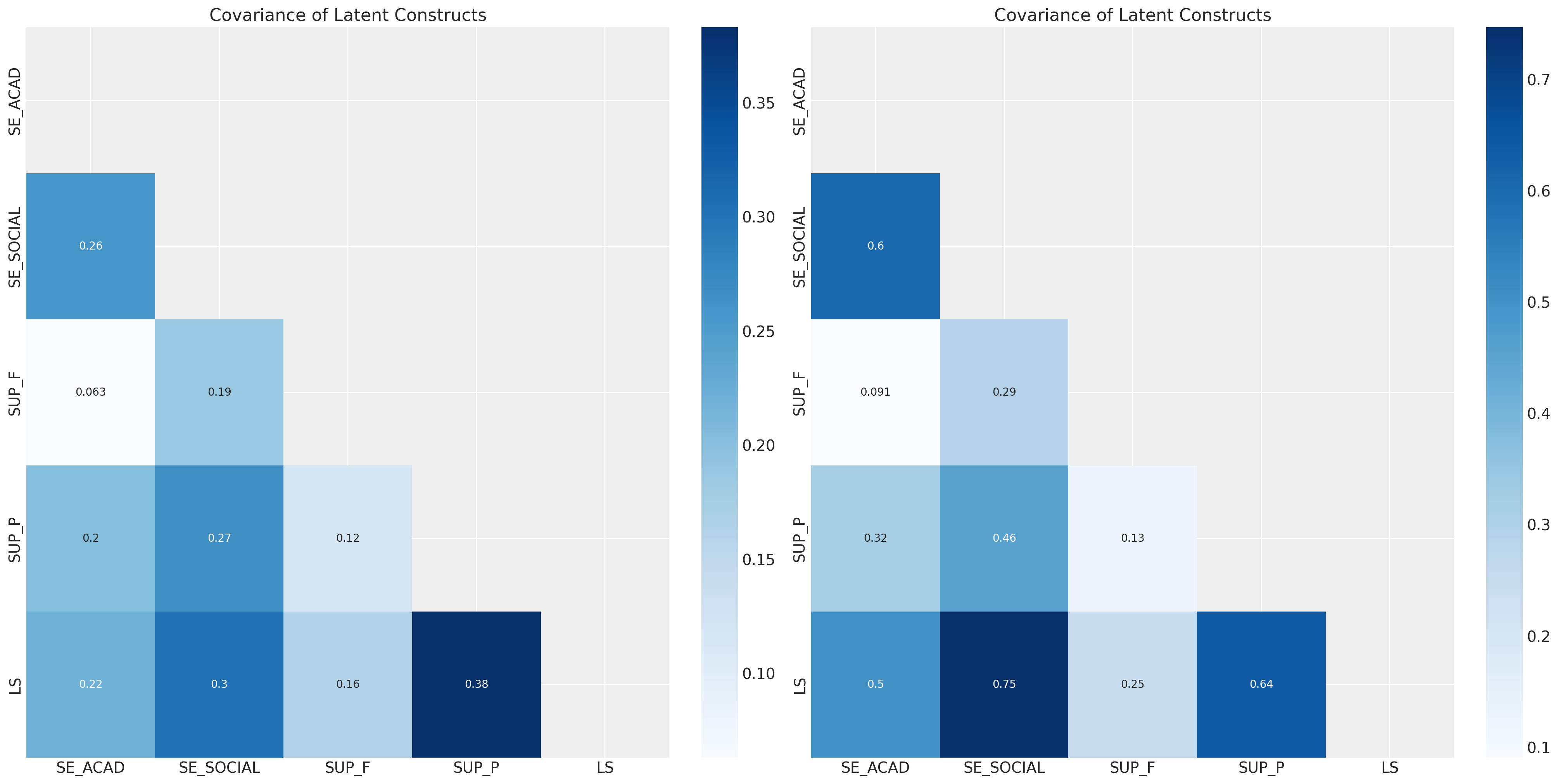
../_images/ec87778b71040e903eefec8a5858dbccb3a4b9b803a9590b9aa7b524527f96b1.png

这突出了生活满意度LS结构、父母支持SUP_P和社会自我效能SE_SOCIAL之间的强关系。我们也可以在我们的潜在结构抽取中观察到这些模式

Hide code cell source 
fig, axs = plt.subplots(1, 3, figsize=(15, 10))
axs = axs.flatten()
ax = axs[0]
ax1 = axs[1]
ax2 = axs[2]
az.plot_forest(idata_mm, var_names=["ksi"], combined=True, ax=ax, coords={"latent": ["SUP_P"]})
az.plot_forest(
    idata_mm,
    var_names=["ksi"],
    combined=True,
    ax=ax1,
    colors="forestgreen",
    coords={"latent": ["SE_SOCIAL"]},
)
az.plot_forest(
    idata_mm,
    var_names=["ksi"],
    combined=True,
    ax=ax2,
    colors="slateblue",
    coords={"latent": ["LS"]},
)
ax.set_yticklabels([])
ax.set_xlabel("SUP_P")
ax1.set_yticklabels([])
ax1.set_xlabel("SE_SOCIAL")
ax2.set_yticklabels([])
ax2.set_xlabel("LS")
ax.axvline(-2, color="red")
ax1.axvline(-2, color="red")
ax2.axvline(-2, color="red")
ax.set_title("Individual Parental Support Metric \n On Latent Factor SUP_P")
ax1.set_title("Individual Social Self Efficacy \n On Latent Factor SE_SOCIAL")
ax2.set_title("Individual Life Satisfaction Metric \n On Latent Factor LS")
plt.show();
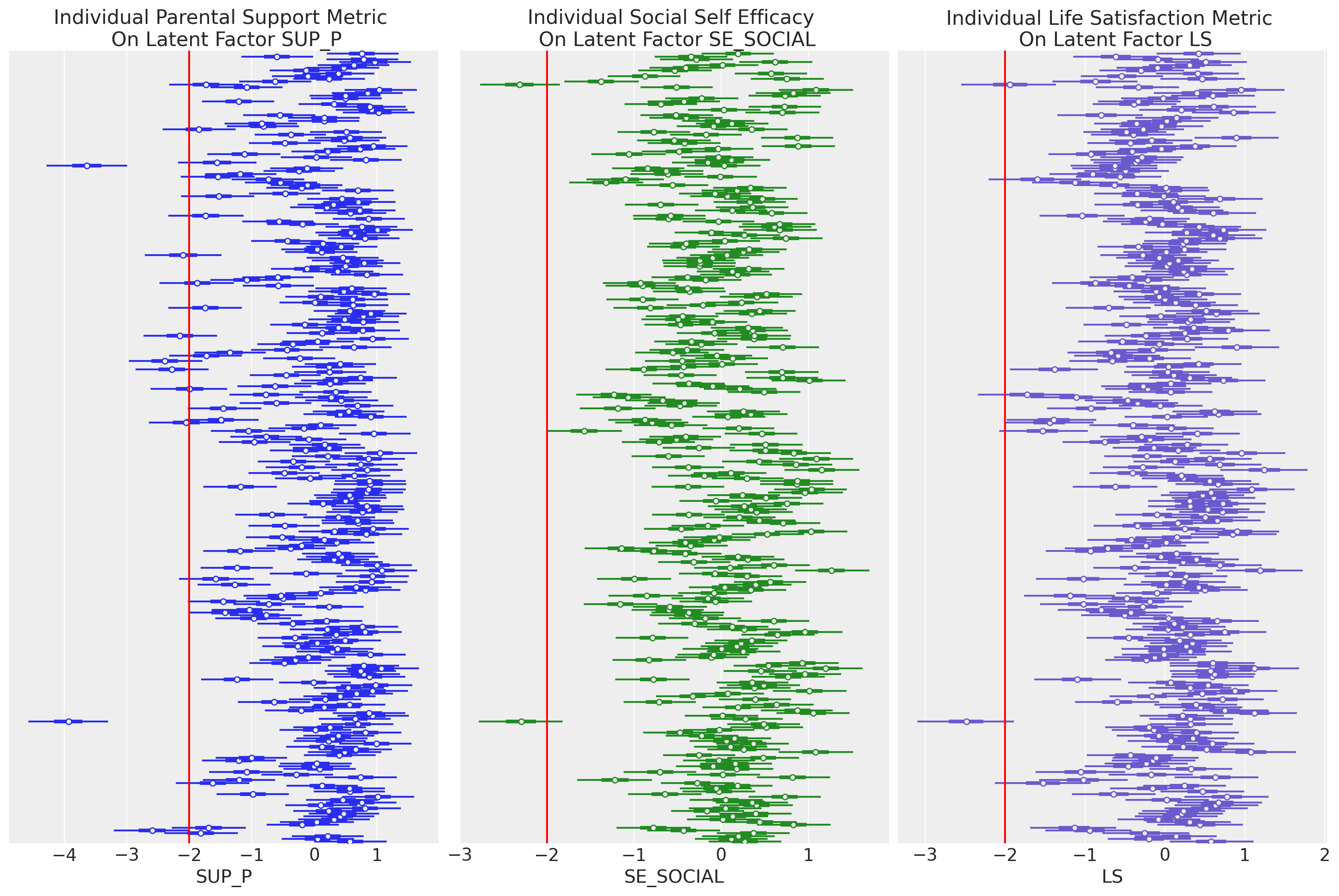
../_images/d4f878c84a78103fda35b6e78442b2ad929b90e7f4dc29532a7903f370f9f341.png

这里值得强调的是，SUP_P 图左上角的群体，其父母支持分数较低，似乎 SE_SOCIAL 分数也较不严重。这种组合似乎导致了相当标准的 LS 分数，表明某种调节关系。

贝叶斯结构方程模型#

我们现在了解了测量模型如何以一种粗略的方式帮助我们理解不同指标变量之间的关系。我们假设了一个潜在因素系统，并推导出这些因素之间的相关性，以帮助我们理解感兴趣的更广泛结构之间的关系强度。这是结构方程模型的一种特殊情况。在SEM传统中，我们感兴趣的是弄清楚变量之间结构关系的各个方面，这意味着我们想要假设依赖和独立关系，以检验我们对系统中影响流动的信念。

对于我们的数据集，我们可以假设以下依赖链

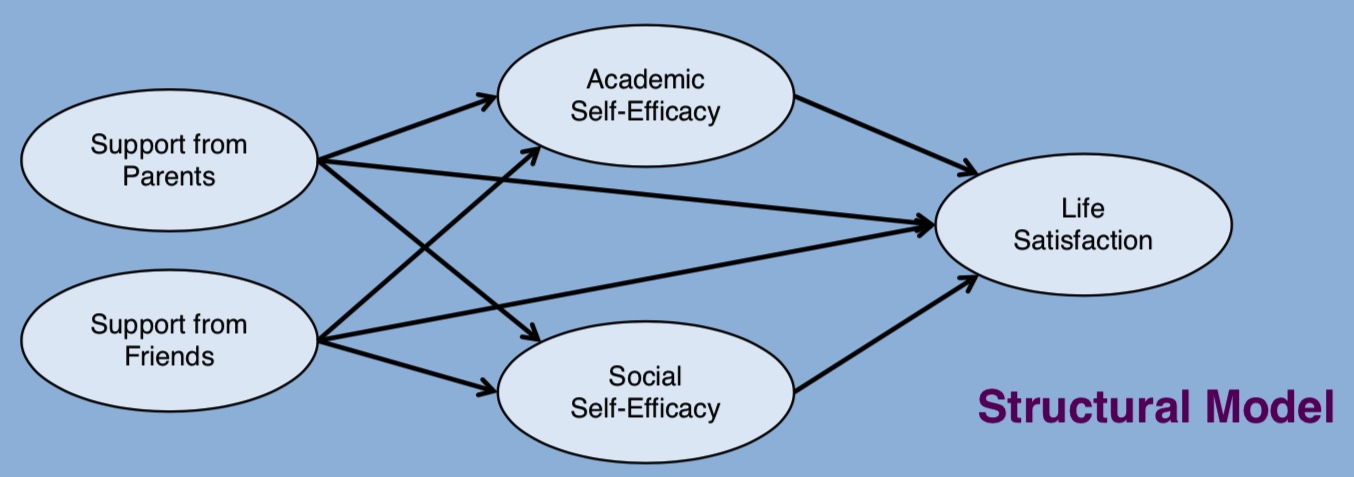
候选结构模型

这张图片介绍了依赖性的具体主张，然后问题就变成了如何对这些模式进行建模？在下一节中，我们将基于基本测量模型的结构，将这些依赖链表述为“根”构念的函数方程。这使得我们能够像以前一样评估模型的充分性问题，但此外，我们现在可以提出关于潜在构念之间直接和间接关系的问题。特别是，由于我们的重点是驱动生活满意度的因素，我们可以向模型询问父母和同伴支持的中介效应。

模型复杂性与贝叶斯敏感性分析#

这些模型已经很复杂了，现在我们又向模型中添加了许多新的参数和结构。每个参数都配备了一个先验，用于塑造模型规范的含义。这是一个非常灵活的框架，我们可以在其中编码各种依赖关系和相关性。有了这种构建推理模型的自由度，我们需要小心评估我们推论的稳健性。因此，我们在这里将进行一个快速的敏感性分析，以展示在不同的先验设置下，该模型的核心含义如何变化。

drivers = [
    "se_acad_p1",
    "se_acad_p2",
    "se_acad_p3",
    "se_social_p1",
    "se_social_p2",
    "se_social_p3",
    "sup_friends_p1",
    "sup_friends_p2",
    "sup_friends_p3",
    "sup_parents_p1",
    "sup_parents_p2",
    "sup_parents_p3",
    "ls_p1",
    "ls_p2",
    "ls_p3",
]


def make_indirect_sem(priors):

    coords = {
        "obs": list(range(len(df))),
        "indicators": drivers,
        "indicators_1": ["se_acad_p1", "se_acad_p2", "se_acad_p3"],
        "indicators_2": ["se_social_p1", "se_social_p2", "se_social_p3"],
        "indicators_3": ["sup_friends_p1", "sup_friends_p2", "sup_friends_p3"],
        "indicators_4": ["sup_parents_p1", "sup_parents_p2", "sup_parents_p3"],
        "indicators_5": ["ls_p1", "ls_p2", "ls_p3"],
        "latent": ["SUP_F", "SUP_P"],
        "latent1": ["SUP_F", "SUP_P"],
        "latent_regression": ["SUP_F->SE_ACAD", "SUP_P->SE_ACAD", "SUP_F->SE_SOC", "SUP_P->SE_SOC"],
        "regression": ["SE_ACAD", "SE_SOCIAL", "SUP_F", "SUP_P"],
    }

    obs_idx = list(range(len(df)))
    with pm.Model(coords=coords) as model:

        Psi = pm.InverseGamma("Psi", 5, 10, dims="indicators")
        lambdas_ = pm.Normal(
            "lambdas_1", priors["lambda"][0], priors["lambda"][1], dims=("indicators_1")
        )
        lambdas_1 = pm.Deterministic(
            "lambdas1", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_1")
        )
        lambdas_ = pm.Normal(
            "lambdas_2", priors["lambda"][0], priors["lambda"][1], dims=("indicators_2")
        )
        lambdas_2 = pm.Deterministic(
            "lambdas2", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_2")
        )
        lambdas_ = pm.Normal(
            "lambdas_3", priors["lambda"][0], priors["lambda"][1], dims=("indicators_3")
        )
        lambdas_3 = pm.Deterministic(
            "lambdas3", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_3")
        )
        lambdas_ = pm.Normal(
            "lambdas_4", priors["lambda"][0], priors["lambda"][1], dims=("indicators_4")
        )
        lambdas_4 = pm.Deterministic(
            "lambdas4", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_4")
        )
        lambdas_ = pm.Normal(
            "lambdas_5", priors["lambda"][0], priors["lambda"][1], dims=("indicators_5")
        )
        lambdas_5 = pm.Deterministic(
            "lambdas5", pt.set_subtensor(lambdas_[0], 1), dims=("indicators_5")
        )
        tau = pm.Normal("tau", 3, 0.5, dims="indicators")
        kappa = 0
        sd_dist = pm.Exponential.dist(1.0, shape=2)
        chol, _, _ = pm.LKJCholeskyCov(
            "chol_cov", n=2, eta=priors["eta"], sd_dist=sd_dist, compute_corr=True
        )
        cov = pm.Deterministic("cov", chol.dot(chol.T), dims=("latent", "latent1"))
        ksi = pm.MvNormal("ksi", kappa, chol=chol, dims=("obs", "latent"))

        # Regression Components
        beta_r = pm.Normal("beta_r", 0, priors["beta_r"], dims="latent_regression")
        beta_r2 = pm.Normal("beta_r2", 0, priors["beta_r2"], dims="regression")
        sd_dist1 = pm.Exponential.dist(1.0, shape=2)
        resid_chol, _, _ = pm.LKJCholeskyCov(
            "resid_chol", n=2, eta=3, sd_dist=sd_dist1, compute_corr=True
        )
        _ = pm.Deterministic("resid_cov", chol.dot(chol.T))
        sigmas_resid = pm.MvNormal("sigmas_resid", kappa, chol=resid_chol)

        # SE_ACAD ~ SUP_FRIENDS + SUP_PARENTS
        regression_se_acad = pm.Normal(
            "regr_se_acad",
            beta_r[0] * ksi[obs_idx, 0] + beta_r[1] * ksi[obs_idx, 1],
            sigmas_resid[0],
        )
        # SE_SOCIAL ~ SUP_FRIENDS + SUP_PARENTS

        regression_se_social = pm.Normal(
            "regr_se_social",
            beta_r[2] * ksi[obs_idx, 0] + beta_r[3] * ksi[obs_idx, 1],
            sigmas_resid[1],
        )

        # LS ~ SE_ACAD + SE_SOCIAL + SUP_FRIEND + SUP_PARENTS
        regression = pm.Normal(
            "regr",
            beta_r2[0] * regression_se_acad
            + beta_r2[1] * regression_se_social
            + beta_r2[2] * ksi[obs_idx, 0]
            + beta_r2[3] * ksi[obs_idx, 1],
            1,
        )

        m0 = tau[0] + regression_se_acad * lambdas_1[0]
        m1 = tau[1] + regression_se_acad * lambdas_1[1]
        m2 = tau[2] + regression_se_acad * lambdas_1[2]
        m3 = tau[3] + regression_se_social * lambdas_2[0]
        m4 = tau[4] + regression_se_social * lambdas_2[1]
        m5 = tau[5] + regression_se_social * lambdas_2[2]
        m6 = tau[6] + ksi[obs_idx, 0] * lambdas_3[0]
        m7 = tau[7] + ksi[obs_idx, 0] * lambdas_3[1]
        m8 = tau[8] + ksi[obs_idx, 0] * lambdas_3[2]
        m9 = tau[9] + ksi[obs_idx, 1] * lambdas_4[0]
        m10 = tau[10] + ksi[obs_idx, 1] * lambdas_4[1]
        m11 = tau[11] + ksi[obs_idx, 1] * lambdas_4[2]
        m12 = tau[12] + regression * lambdas_5[0]
        m13 = tau[13] + regression * lambdas_5[1]
        m14 = tau[14] + regression * lambdas_5[2]

        mu = pm.Deterministic(
            "mu", pm.math.stack([m0, m1, m2, m3, m4, m5, m6, m7, m8, m9, m10, m11, m12, m13, m14]).T
        )
        _ = pm.Normal("likelihood", mu, Psi, observed=df[drivers].values)

        idata = pm.sample(
            10_000,
            chains=4,
            nuts_sampler="numpyro",
            target_accept=0.99,
            tune=2000,
            idata_kwargs={"log_likelihood": True},
            random_seed=110,
        )
        idata.extend(pm.sample_posterior_predictive(idata))

        return model, idata


model_sem0, idata_sem0 = make_indirect_sem(
    priors={"eta": 2, "lambda": [1, 1], "beta_r": 0.1, "beta_r2": 0.1}
)
model_sem1, idata_sem1 = make_indirect_sem(
    priors={"eta": 2, "lambda": [1, 1], "beta_r": 0.2, "beta_r2": 0.2}
)
model_sem2, idata_sem2 = make_indirect_sem(
    priors={"eta": 2, "lambda": [1, 1], "beta_r": 0.5, "beta_r2": 0.5}
)

Compiling...
Compilation time = 0:00:11.696197
Sampling...

Sampling time = 0:01:08.103534
Transforming variables...
Transformation time = 0:00:03.042150
Computing Log Likelihood...
Log Likelihood time = 0:00:01.889064
Sampling: [likelihood]
100.00% [40000/40000 00:04<00:00] 
Compiling...
Compilation time = 0:00:11.975201
Sampling...

Sampling time = 0:01:08.567877
Transforming variables...
Transformation time = 0:00:03.029417
Computing Log Likelihood...
Log Likelihood time = 0:00:02.128598
Sampling: [likelihood]
100.00% [40000/40000 00:04<00:00] 
Compiling...
Compilation time = 0:00:12.106062
Sampling...

Sampling time = 0:01:07.131131
Transforming variables...
Transformation time = 0:00:03.069262
Computing Log Likelihood...
Log Likelihood time = 0:00:01.810234
Sampling: [likelihood]
100.00% [40000/40000 00:04<00:00]

主要需要观察的结构特征是，我们现在已经在模型中添加了许多回归，使得我们在测量模型中作为给定的一些构念现在被表示为其他构念的线性组合。因为我们去除了SE_SOCIAL和SE_ACAD之间的相关效应，我们通过在它们的回归方程中添加相关误差项来重新引入它们之间的相关性。在lavaan语法中，我们追求的是类似的东西。

Measurement model
SUP_Parents =~ sup_parents_p1 + sup_parents_p2 + sup_parents_p3
SUP_Friends =~ sup_friends_p1 + sup_friends_p2 + sup_friends_p3
SE_Academic =~ se_acad_p1 + se_acad_p2 + se_acad_p3
SE_Social =~ se_social_p1 + se_social_p2 + se_social_p3
LS  =~ ls_p1 + ls_p2 + ls_p3

Regressions
SE_Academic ~ SUP_Parents + SUP_Friends
SE_Social ~ SUP_Parents + SUP_Friends
LS ~ SE_Academic + SE_Social + SUP_Parents + SUP_Friends

Residual covariances
SE_Academic ~~ SE_Social

pm.model_to_graphviz(model_sem0)
../_images/eac0e0b0fd411a8f254457404e693fadc28fd8845672b3d0e87e171a4b1d0b33.svg

值得暂停一下，来审视一下这个图中所描绘的依赖关系的本质。我们可以看到，我们如何替换了更简单的测量模型结构，并添加了三个回归函数，这些函数取代了从多元正态分布 \(Ksi\) 中抽取的样本。换句话说，我们已经在同一个模型中表达了一系列回归的依赖关系。接下来，我们将看到参数估计值如何在我们对模型的先验规范中发生变化。请注意，与回归系数相比，因子载荷的相对稳定性。

fig, ax = plt.subplots(figsize=(15, 15))
az.plot_forest(
    [idata_sem0, idata_sem1, idata_sem2],
    model_names=["SEM0", "SEM1", "SEM2"],
    var_names=["lambdas1", "lambdas2", "lambdas3", "lambdas4", "lambdas5", "beta_r", "beta_r2"],
    combined=True,
    ax=ax,
);
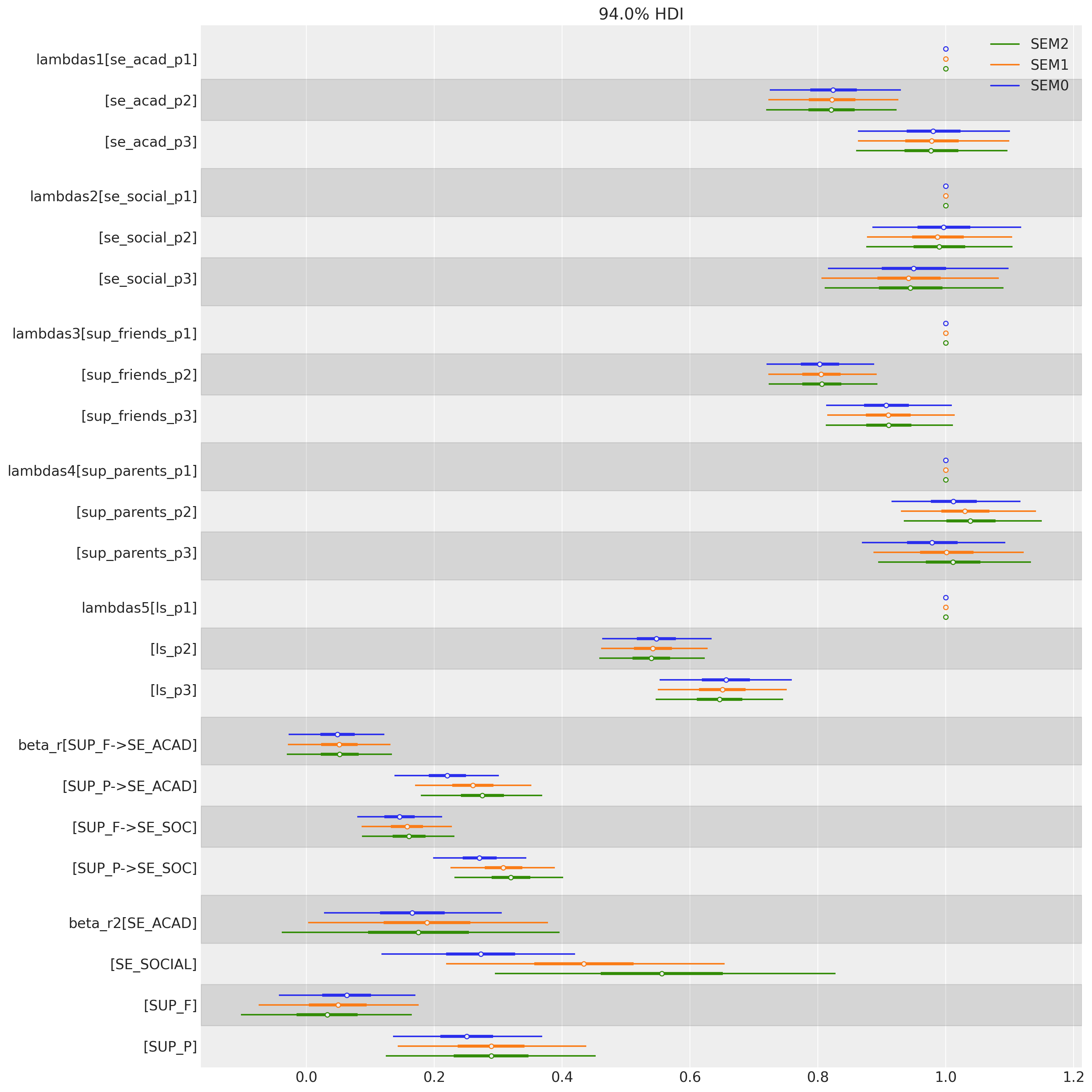
../_images/ad7c42ff37b4fe41a25e35db270d8ae100cc1eaad0de0e9390596b511eb259a6.png

模型评估检查#

对模型性能的快速评估表明，我们在恢复样本协方差结构方面做得不如在更简单的测量模型中那么好。

residuals_posterior_cov = get_posterior_resids(idata_sem0, 2500)
residuals_posterior_corr = get_posterior_resids(idata_sem0, 2500, metric="corr")

fig, ax = plt.subplots(figsize=(20, 10))
mask = np.triu(np.ones_like(residuals_posterior_corr, dtype=bool))
ax = sns.heatmap(residuals_posterior_corr, annot=True, cmap="bwr", center=0, mask=mask)
ax.set_title("Residuals between Model Implied and Sample Correlations", fontsize=25);
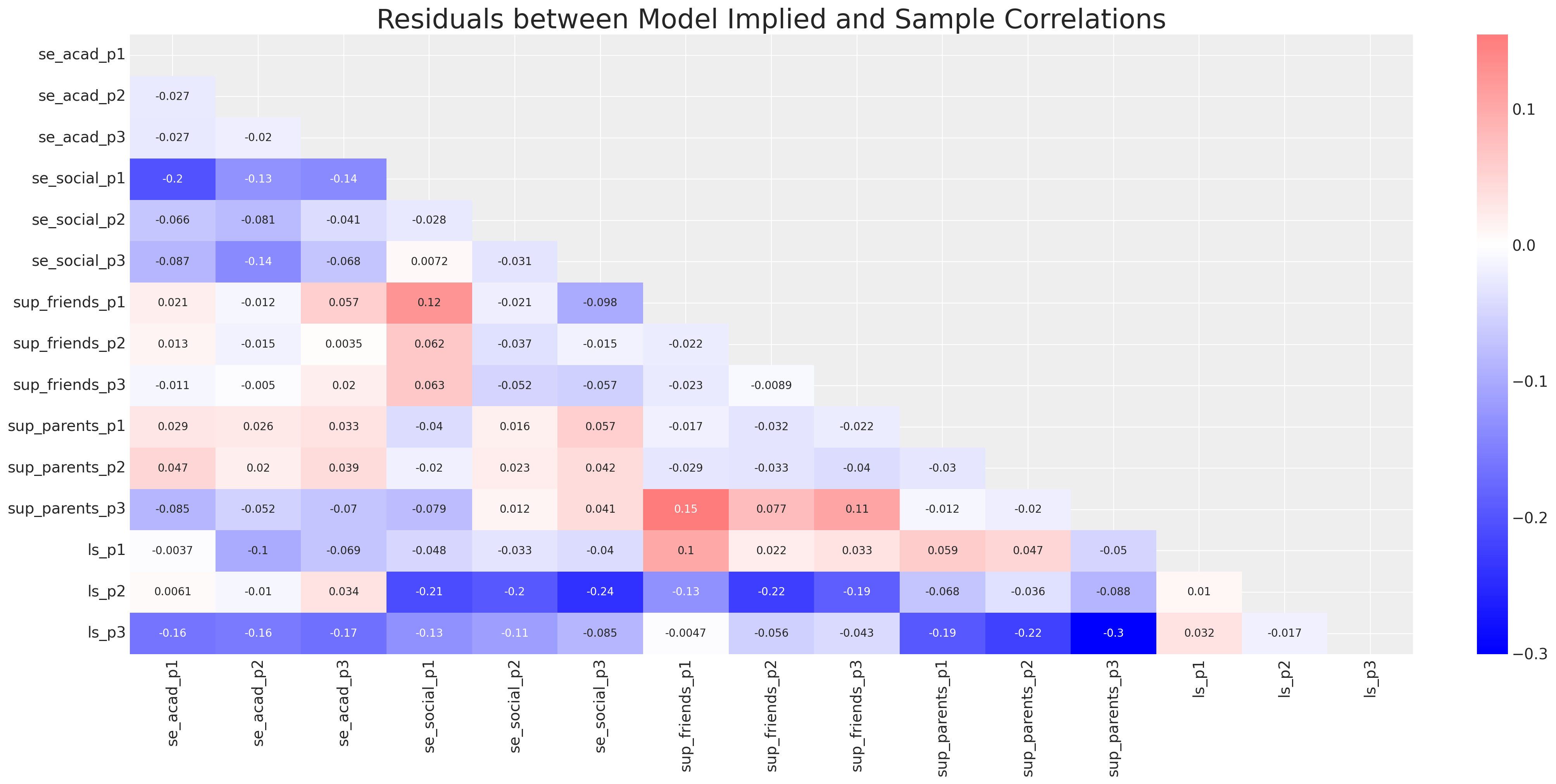
../_images/aa5821bd527af95dde0eeb07e24d77f87a83087928647402b48787ab4361e537.png

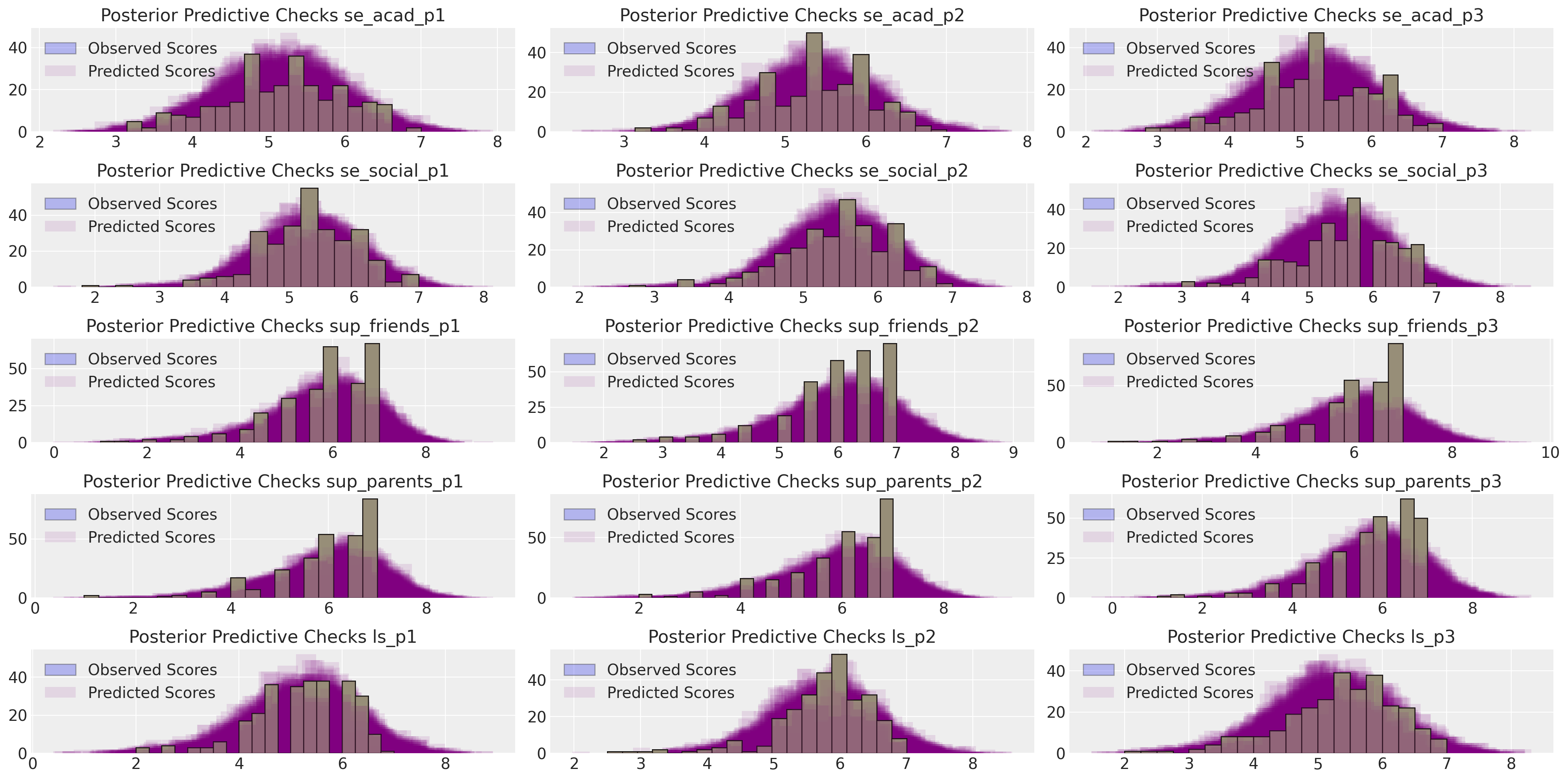
但后验预测检查看起来仍然合理。我们的生活满意度焦点量似乎得到了很好的恢复。

make_ppc(idata_sem0, 100, drivers=drivers, dims=(5, 3))
../_images/7e51874bfe68c09c5d80c3ef8602297e782ed993fe04d78693cfdcb1fae6931c.png

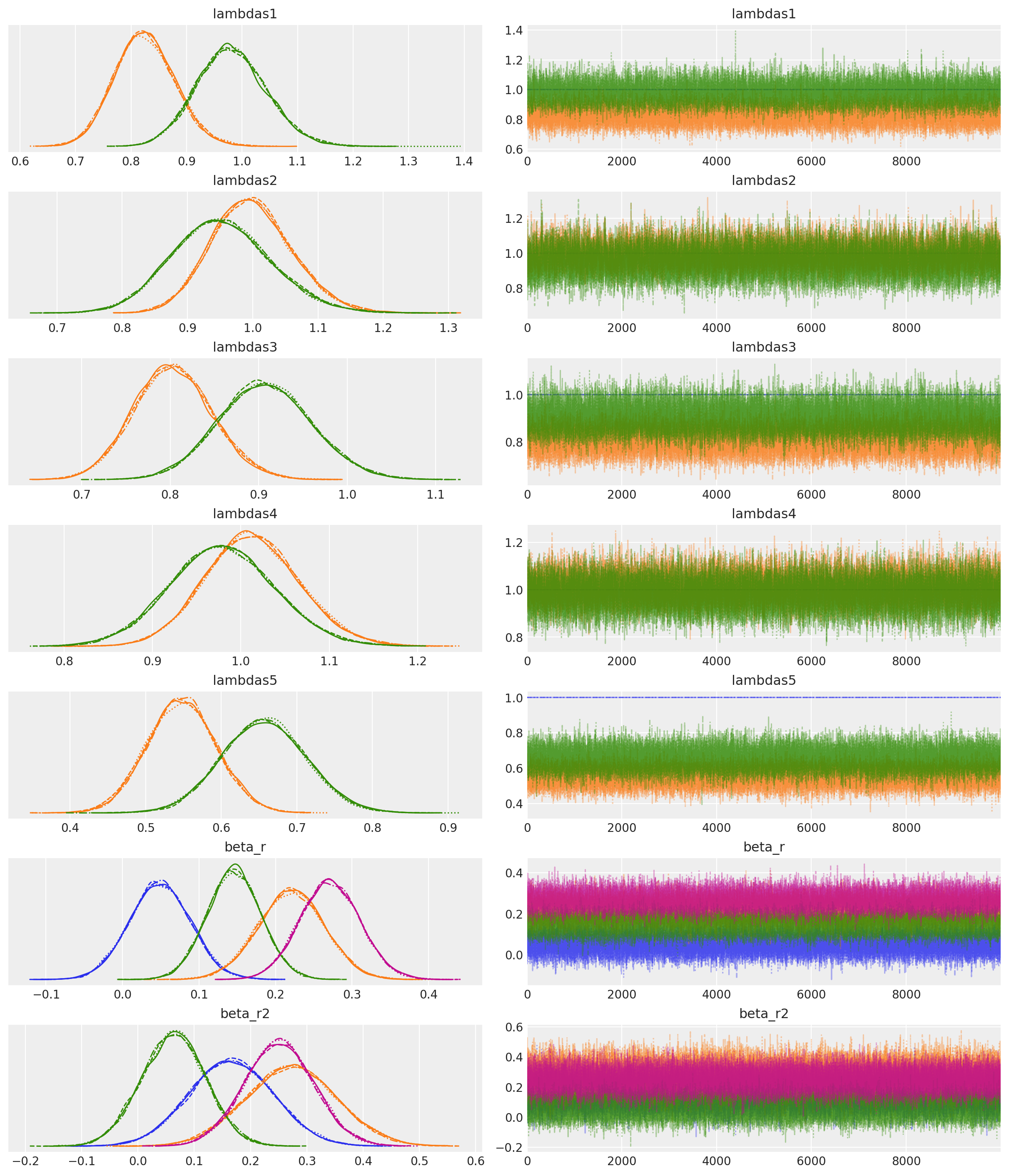
模型诊断显示总体上健康的跟踪图，存在一些分歧，但有效样本量和r-hat指标都很好，因此我们应该对模型很好地收敛到后验分布感到相当满意。

az.plot_trace(
    idata_sem0,
    var_names=["lambdas1", "lambdas2", "lambdas3", "lambdas4", "lambdas5", "beta_r", "beta_r2"],
);
../_images/95e8c3b18b62f0a5f0db50f9fe2793357d62954e0a1bc6023f899af3c04fb59a.png 
az.summary(
    idata_sem0,
    var_names=[
        "lambdas1",
        "lambdas2",
        "lambdas3",
        "lambdas4",
        "lambdas5",
        "beta_r",
        "beta_r2",
        "Psi",
        "tau",
    ],
)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
lambdas1[se_acad_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas1[se_acad_p2] 0.825 0.055 0.725 0.930 0.001 0.000 9636.0 15616.0 1.0
lambdas1[se_acad_p3] 0.982 0.063 0.863 1.101 0.001 0.000 8860.0 14667.0 1.0
lambdas2[se_social_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas2[se_social_p2] 0.999 0.062 0.885 1.118 0.001 0.001 5688.0 9867.0 1.0
lambdas2[se_social_p3] 0.952 0.075 0.816 1.098 0.001 0.001 9841.0 16162.0 1.0
lambdas3[sup_friends_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas3[sup_friends_p2] 0.804 0.045 0.720 0.888 0.000 0.000 10940.0 18878.0 1.0
lambdas3[sup_friends_p3] 0.908 0.052 0.813 1.010 0.000 0.000 12075.0 20292.0 1.0
lambdas4[sup_parents_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas4[sup_parents_p2] 1.013 0.054 0.915 1.117 0.001 0.000 8953.0 15516.0 1.0
lambdas4[sup_parents_p3] 0.979 0.059 0.869 1.093 0.001 0.000 12016.0 19450.0 1.0
lambdas5[ls_p1] 1.000 0.000 1.000 1.000 0.000 0.000 40000.0 40000.0 NaN
lambdas5[ls_p2] 0.547 0.046 0.463 0.634 0.000 0.000 23600.0 28513.0 1.0
lambdas5[ls_p3] 0.656 0.056 0.552 0.759 0.000 0.000 21916.0 27988.0 1.0
beta_r[SUP_F->SE_ACAD] 0.049 0.040 -0.028 0.122 0.000 0.000 33619.0 30265.0 1.0
beta_r[SUP_P->SE_ACAD] 0.220 0.043 0.138 0.301 0.000 0.000 26087.0 27608.0 1.0
beta_r[SUP_F->SE_SOC] 0.146 0.035 0.080 0.213 0.000 0.000 26552.0 29710.0 1.0
beta_r[SUP_P->SE_SOC] 0.271 0.039 0.198 0.344 0.000 0.000 18597.0 25964.0 1.0
beta_r2[SE_ACAD] 0.166 0.074 0.028 0.305 0.000 0.000 41792.0 31794.0 1.0
beta_r2[SE_SOCIAL] 0.272 0.080 0.118 0.420 0.000 0.000 42014.0 31550.0 1.0
beta_r2[SUP_F] 0.063 0.057 -0.043 0.171 0.000 0.000 34544.0 27449.0 1.0
beta_r2[SUP_P] 0.251 0.062 0.136 0.369 0.000 0.000 29584.0 30999.0 1.0
Psi[se_acad_p1] 0.417 0.029 0.362 0.471 0.000 0.000 11409.0 16465.0 1.0
Psi[se_acad_p2] 0.413 0.024 0.366 0.457 0.000 0.000 19369.0 24906.0 1.0
Psi[se_acad_p3] 0.462 0.028 0.408 0.516 0.000 0.000 17531.0 22823.0 1.0
Psi[se_social_p1] 0.444 0.027 0.394 0.494 0.000 0.000 14886.0 22035.0 1.0
Psi[se_social_p2] 0.338 0.026 0.291 0.389 0.000 0.000 10327.0 17290.0 1.0
Psi[se_social_p3] 0.557 0.029 0.503 0.610 0.000 0.000 29639.0 29036.0 1.0
Psi[sup_friends_p1] 0.517 0.039 0.444 0.591 0.000 0.000 10615.0 15242.0 1.0
Psi[sup_friends_p2] 0.508 0.031 0.450 0.566 0.000 0.000 18625.0 24298.0 1.0
Psi[sup_friends_p3] 0.624 0.036 0.556 0.691 0.000 0.000 21581.0 25635.0 1.0
Psi[sup_parents_p1] 0.541 0.035 0.477 0.609 0.000 0.000 14766.0 22528.0 1.0
Psi[sup_parents_p2] 0.537 0.037 0.468 0.605 0.000 0.000 13008.0 18715.0 1.0
Psi[sup_parents_p3] 0.684 0.038 0.612 0.754 0.000 0.000 21999.0 26864.0 1.0
Psi[ls_p1] 0.537 0.051 0.442 0.633 0.001 0.000 6824.0 10978.0 1.0
Psi[ls_p2] 0.552 0.030 0.496 0.608 0.000 0.000 21921.0 25170.0 1.0
Psi[ls_p3] 0.670 0.036 0.603 0.740 0.000 0.000 19160.0 24500.0 1.0
tau[se_acad_p1] 5.058 0.048 4.966 5.148 0.001 0.001 4545.0 10287.0 1.0
tau[se_acad_p2] 5.266 0.042 5.186 5.345 0.001 0.000 5105.0 12105.0 1.0
tau[se_acad_p3] 5.115 0.049 5.022 5.208 0.001 0.000 4915.0 12071.0 1.0
tau[se_social_p1] 5.175 0.046 5.087 5.262 0.001 0.001 3954.0 9674.0 1.0
tau[se_social_p2] 5.364 0.043 5.283 5.444 0.001 0.001 3632.0 8857.0 1.0
tau[se_social_p3] 5.327 0.049 5.236 5.421 0.001 0.000 5021.0 11942.0 1.0
tau[sup_friends_p1] 5.607 0.070 5.473 5.735 0.001 0.001 3545.0 7220.0 1.0
tau[sup_friends_p2] 5.864 0.059 5.754 5.979 0.001 0.001 3903.0 8593.0 1.0
tau[sup_friends_p3] 5.822 0.068 5.696 5.954 0.001 0.001 4102.0 8858.0 1.0
tau[sup_parents_p1] 5.769 0.068 5.641 5.895 0.001 0.001 3000.0 7066.0 1.0
tau[sup_parents_p2] 5.719 0.068 5.587 5.843 0.001 0.001 3132.0 7931.0 1.0
tau[sup_parents_p3] 5.512 0.071 5.378 5.644 0.001 0.001 3647.0 9103.0 1.0
tau[ls_p1] 5.010 0.073 4.873 5.149 0.001 0.001 4056.0 9242.0 1.0
tau[ls_p2] 5.671 0.050 5.578 5.765 0.001 0.000 5777.0 13336.0 1.0
tau[ls_p3] 5.096 0.060 4.984 5.210 0.001 0.001 5766.0 12740.0 1.0

其他模型的类似诊断结果也成立。我们现在继续评估在更简单的测量模型中模糊的直接和间接效应问题。我的意思是，我们追踪影响生活满意度的总路径，并评估由于父母和同伴支持的相对影响强度。

间接和直接效应#

我们现在转向我们在模型图中编码的附加回归结构。首先我们提取回归系数

fig, axs = plt.subplots(1, 2, figsize=(20, 8))

az.plot_energy(idata_sem0, ax=axs[0])

az.plot_forest(idata_sem0, var_names=["beta_r", "beta_r2"], combined=True, ax=axs[1])
axs[1].axvline(0, color="red", label="zero-effect")
axs[1].legend();
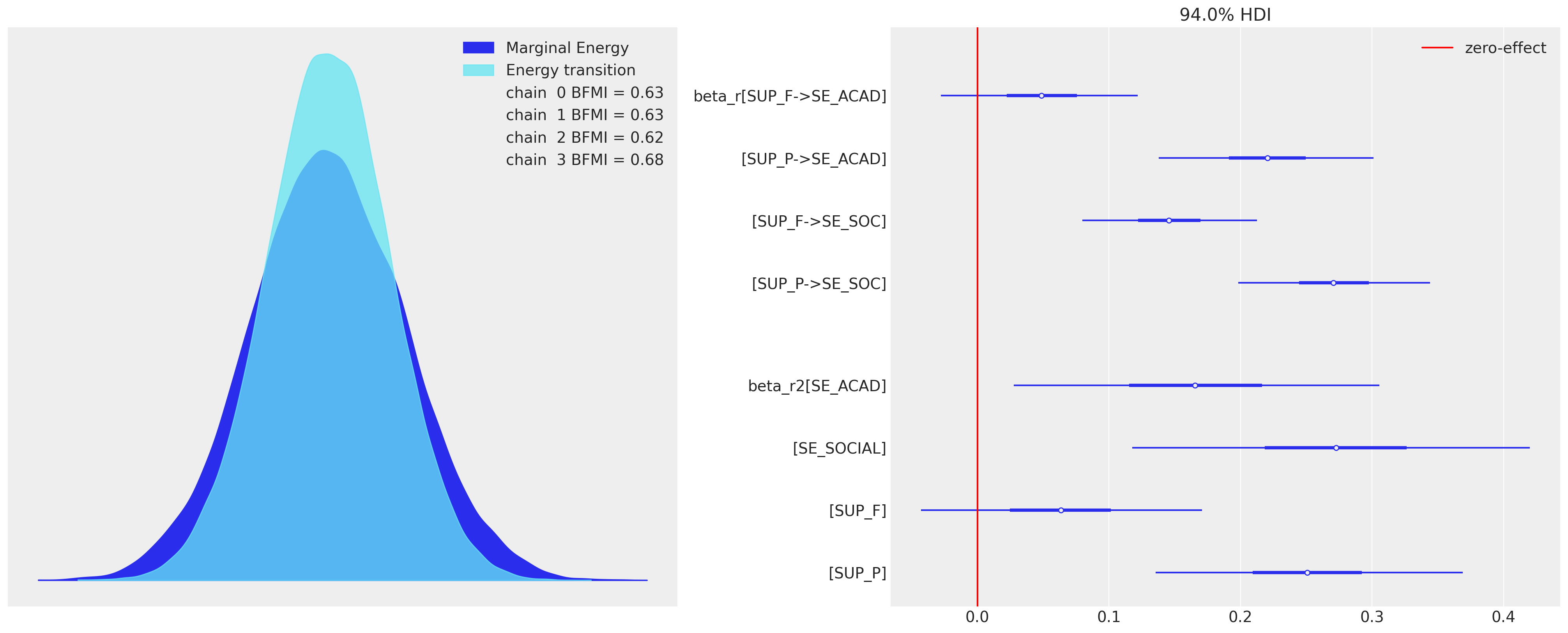
../_images/14eb9491b9267bf08151c2374e71258769f8f15bfaec4189e4bc82943a4f1441.png

系数表明，与父母支持相比，同伴支持的相对权重较小。当我们通过我们的DAG或回归系数链追踪累积的因果效应（直接和间接）时，这一点得到了证实。

def calculate_effects(idata, var="SUP_P"):
    summary_df = az.summary(idata, var_names=["beta_r", "beta_r2"])
    # Indirect Paths
    ## VAR -> SE_SOC ->LS
    indirect_parent_soc = (
        summary_df.loc[f"beta_r[{var}->SE_SOC]"]["mean"]
        * summary_df.loc["beta_r2[SE_SOCIAL]"]["mean"]
    )

    ## VAR -> SE_SOC ->LS
    indirect_parent_acad = (
        summary_df.loc[f"beta_r[{var}->SE_ACAD]"]["mean"]
        * summary_df.loc["beta_r2[SE_ACAD]"]["mean"]
    )

    ## Total Indirect Effects
    total_indirect = indirect_parent_soc + indirect_parent_acad

    ## Total Effects
    total_effect = total_indirect + summary_df.loc[f"beta_r2[{var}]"]["mean"]

    return pd.DataFrame(
        [[indirect_parent_soc, indirect_parent_acad, total_indirect, total_effect]],
        columns=[
            f"{var} -> SE_SOC ->LS",
            f"{var} -> SE_ACAD ->LS",
            f"Total Indirect Effects {var}",
            f"Total Effects {var}",
        ],
    )

重要的是，我们在这里看到了先验对隐含关系的影响。当我们把先验拉近到0时，父母支持的总效应被向下拉离了0.5，而同伴支持则相对稳定在0.10左右。然而，父母支持的影响仍然明显大于同伴支持的影响。

summary_p = pd.concat(
    [calculate_effects(idata_sem0), calculate_effects(idata_sem1), calculate_effects(idata_sem2)]
)

summary_p.index = ["SEM0", "SEM1", "SEM2"]
summary_p
SUP_P -> SE_SOC ->LS SUP_P -> SE_ACAD ->LS Total Indirect Effects SUP_P Total Effects SUP_P
SEM0 0.073712 0.03652 0.110232 0.361232
SEM1 0.133672 0.04914 0.182812 0.471812
SEM2 0.177920 0.04840 0.226320 0.515320

由于父母支持的估计影响对我们的方差先验的敏感性变化很大。这里有一个实质性的例子，说明了理论选择在模型设计中的作用。我们应该多强烈地相信父母和同伴效应对生活满意度的影响为零？如果我们试图将效应缩小到零，我倾向于认为我们过于保守，应该更喜欢一个不那么保守的模型。然而，这里的例子不是为了争论这个问题，而是为了展示敏感性检查的重要性。

summary_f = pd.concat(
    [
        calculate_effects(idata_sem0, "SUP_F"),
        calculate_effects(idata_sem1, "SUP_F"),
        calculate_effects(idata_sem2, "SUP_F"),
    ]
)

summary_f.index = ["SEM0", "SEM1", "SEM2"]
summary_f
SUP_F -> SE_SOC ->LS SUP_F -> SE_ACAD ->LS Total Indirect Effects SUP_F Total Effects SUP_F
SEM0 0.039712 0.008134 0.047846 0.110846
SEM1 0.068572 0.009828 0.078400 0.127400
SEM2 0.089516 0.009152 0.098668 0.130668

计算全局模型拟合#

我们还可以计算模型的全局拟合度量。这里我们比较了测量模型和我们的SEM模型的各种版本，虽然这种比较有些不公平。SEM模型试图表达更复杂的结构，因此在简单的全局拟合度量上可能会不如相对简单的模型。这种复杂性并非随意，你需要在表达能力和与观测数据点的全局模型拟合之间做出权衡决策。

compare_df = az.compare(
    {"SEM0": idata_sem0, "SEM1": idata_sem1, "SEM2": idata_sem2, "MM": idata_mm}
)
compare_df

/Users/nathanielforde/mambaforge/envs/pymc_causal/lib/python3.11/site-packages/arviz/stats/stats.py:309: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'True' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  df_comp.loc[val] = (
/Users/nathanielforde/mambaforge/envs/pymc_causal/lib/python3.11/site-packages/arviz/stats/stats.py:309: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise an error in a future version of pandas. Value 'log' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
  df_comp.loc[val] = (
rank elpd_loo p_loo elpd_diff weight se dse warning scale
MM 0 -3728.300062 994.604514 0.000000 8.023087e-01 65.332293 0.000000 True log
SEM0 1 -3778.256742 1109.385888 49.956680 1.976913e-01 64.764420 13.618924 True log
SEM1 2 -3781.419677 1104.681730 53.119615 3.276563e-15 64.853007 13.459803 True log
SEM2 3 -3782.787099 1102.006963 54.487037 0.000000e+00 64.871911 13.330740 True log

结论#

我们刚刚看到了如何从思考抽象心理测量结构的测量，通过评估这些潜在结构之间复杂的相关性和协方差模式，到评估潜在因素之间的假设因果结构。这是对心理测量模型以及SEM和CFA模型的表达能力的快速介绍，我们通过将它们与因果推断领域联系起来来结束这一介绍！这并非偶然，而是证明了因果关系问题处于大多数建模工作的核心。当我们对任何类型的复杂变量联合分布感兴趣时，我们很可能对系统的因果结构感兴趣——一些观测指标的实现值如何依赖于或与其它指标相关？重要的是，我们需要理解这些观测是如何实现的，而不会将简单的相关性误认为因果关系，从而避免通过天真或混淆的推断得出错误的结论。

Mislevy 和 Levy 通过关注 De Finetti 定理在通过贝叶斯推断恢复可交换性中的作用，强调了这种联系。根据 De Finetti 定理，可交换序列变量的分布可以表示为条件独立变量的混合。

\[ p(\mathbf{x_{1}}^{T}....\mathbf{x_{q}}^{T}) = \dfrac{p(X | \theta)p(\theta)}{p_{i}(X)} = \dfrac{p(\mathbf{x_{i}}^{T}.....\mathbf{x_{n}}^{T} | \text{Ksi}, \Psi, \tau, \Lambda, \beta)p(\text{Ksi}, \Psi, \tau, \Lambda, \beta) }{p(\mathbf{x_{i}}^{T}.....\mathbf{x_{n}}^{T})} \]

这种表示方法授权了对系统的实质性声明。因此，如果我们正确地指定了条件分布，我们就能恢复那些通过精心设计的模型进行推断的条件，因为受试者的结果在我们模型的条件下被认为是可交换的。混合分布只是我们模型所依赖的参数向量。这在结构方程模型（SEM）和验证性因子分析（CFA）模型中表现得很好，因为我们明确地构建了系统的交互作用，以消除偏倚的依赖结构并授权进行清晰的推断。在固定潜在构念水平的情况下，我们期望能够对指标度量的预期实现做出可推广的声明。

[C]条件独立性不是我们必须被动等待的自然恩赐，而是一种心理上的必要性，我们通过以特定方式组织我们的知识来满足这种必要性。在这种组织中，一个重要的工具是识别出诱导可观测变量之间条件独立的中间变量；如果这些变量不在我们的词汇中，我们就创造它们。例如，在医学诊断中，当某些症状直接相互影响时，医学界会为这种相互作用发明一个名称（例如“综合征”、“并发症”、“病理状态”），并将其视为一个新的辅助变量，诱导条件独立性。” - Pearl 引自 Levy 和 Mislevy [2020] 第61页

正是这种对条件化结构的有意和谨慎的关注，将看似不同的学科——心理测量学和因果推断——统一起来。这两个学科都培养了对数据生成过程结构的仔细思考，并且更进一步，它们提供了条件化策略，以更好地针对某些感兴趣的估计量。两者都可以用像PyMC这样的概率编程语言的表达性词汇很好地表述。我们鼓励您亲自探索丰富的可能性！

作者#

参考资料#

[1]

朱迪亚·珀尔。智能系统中的概率推理：可信推理网络。摩根·考夫曼，1985年。

[2]

罗伊·利维和罗伯特·J·米斯利维。《贝叶斯心理测量建模》。CRC出版社，2020年。

水印#

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Wed Sep 25 2024

Python implementation: CPython
Python version       : 3.11.7
IPython version      : 8.20.0

pytensor: 2.18.6

pandas    : 2.2.0
pymc      : 5.10.3
arviz     : 0.17.0
matplotlib: 3.8.2
pytensor  : 2.18.6
numpy     : 1.24.4
seaborn   : 0.13.2

Watermark: 2.4.3