贝叶斯中介分析#
本笔记本涵盖了贝叶斯中介分析。当我们想要探索预测变量与结果变量之间可能的中介路径时,这是非常有用的。
需要注意的是,中介分析的方法随着时间的推移已经发生了演变。本笔记本深受Hayes [2017]在其教科书《中介、调节和条件过程分析导论》中所提出的方法的影响。
读者应注意,中介分析通常与调节分析混淆,对此我们有一个单独的示例(贝叶斯调节分析)。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns
from pandas import DataFrame
%config InlineBackend.figure_format = 'retina'
plt.rcParams.update({"font.size": 14})
seed = 42
rng = np.random.default_rng(seed);
中介模型#
简单的媒介模型非常简单,其中 \(m\) 是 \(x\) 的线性函数,而 \(y\) 是 \(x\) 和 \(m\) 的线性函数:
其中 \(i\) 表示每个观测值(数据集中的行),而 \(i_M\) 和 \(i_Y\) 是截距参数。注意,\(x_i\)、\(m_i\) 和 \(y_i\) 是观测数据。
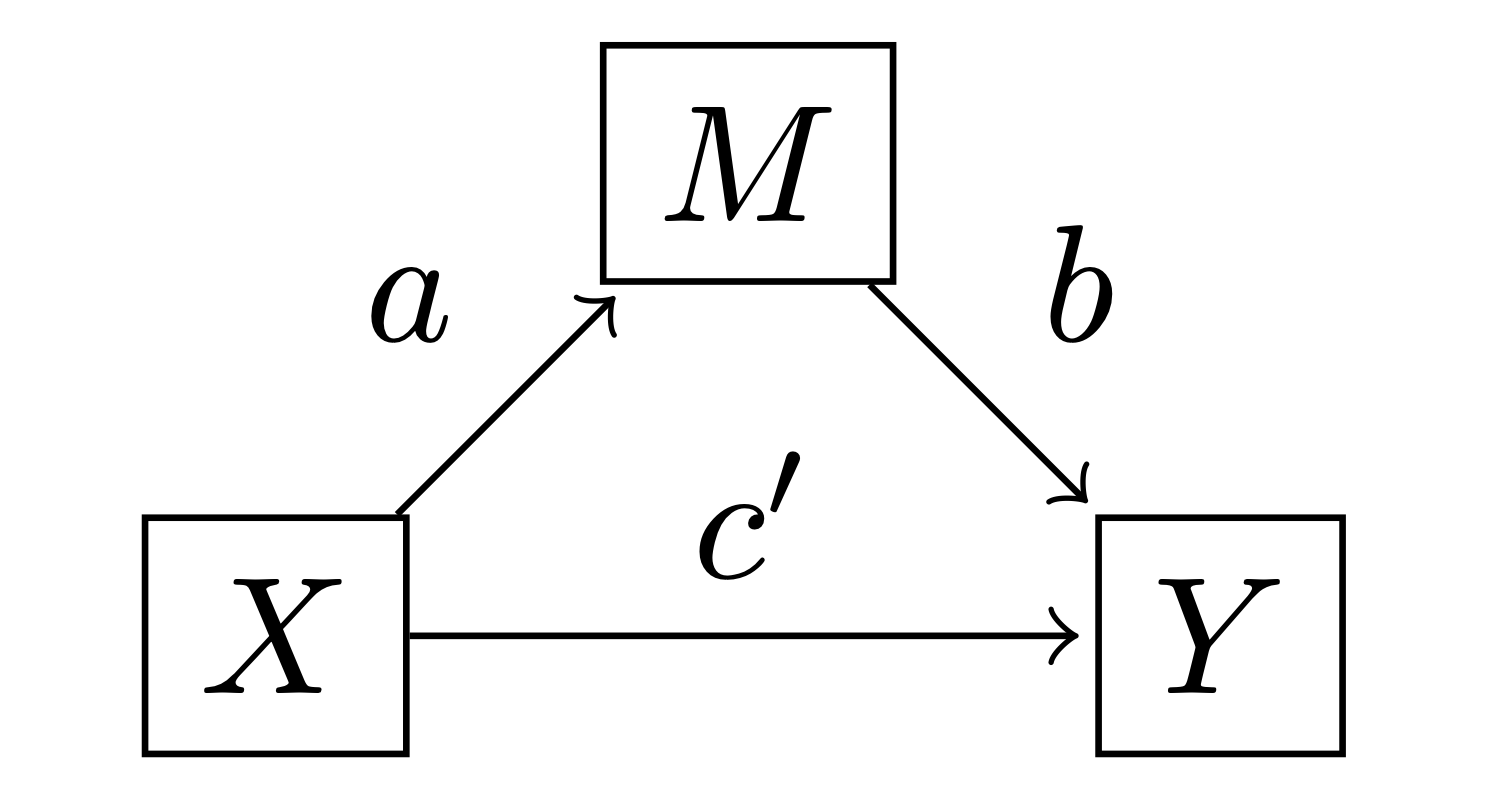
使用来自 Hayes [2017] 的定义,我们可以定义一些感兴趣的效果:
直接效应:由\(c'\)给出。在\(x\)上相差一个单位但在\(m\)上相等的两种情况,估计在\(y\)上相差\(c'\)个单位。
间接效应:由 \(a \cdot b\) 给出。两个相差一个单位 \(x\) 的情况估计在 \(y\) 上相差 \(a \cdot b\) 个单位,这是由于 \(x \rightarrow m\) 和 \(m \rightarrow y\) 的影响。
总效应:是 \(c = c' + a \cdot b\),即直接效应和间接效应的总和。这可以理解为:在 \(x\) 上相差一个单位的两个案例,由于间接路径 \(x \rightarrow m \rightarrow y\),估计在 \(y\) 上相差 \(a \cdot b\) 个单位,由于直接路径 \(x \rightarrow y\),估计相差 \(c'\) 个单位。总效应也可以通过评估替代模型 \(y_i \sim \mathrm{Normal}(i_{Y*} + c \cdot x_i, \sigma_{Y*})\) 来估计。
生成模拟数据#
def make_data():
N = 75
a, b, cprime = 0.5, 0.6, 0.3
im, iy, σm, σy = 2.0, 0.0, 0.5, 0.5
x = rng.normal(loc=0, scale=1, size=N)
m = im + rng.normal(loc=a * x, scale=σm, size=N)
y = iy + (cprime * x) + rng.normal(loc=b * m, scale=σy, size=N)
print(f"True direct effect = {cprime}")
print(f"True indirect effect = {a*b}")
print(f"True total effect = {cprime+a*b}")
return x, m, y
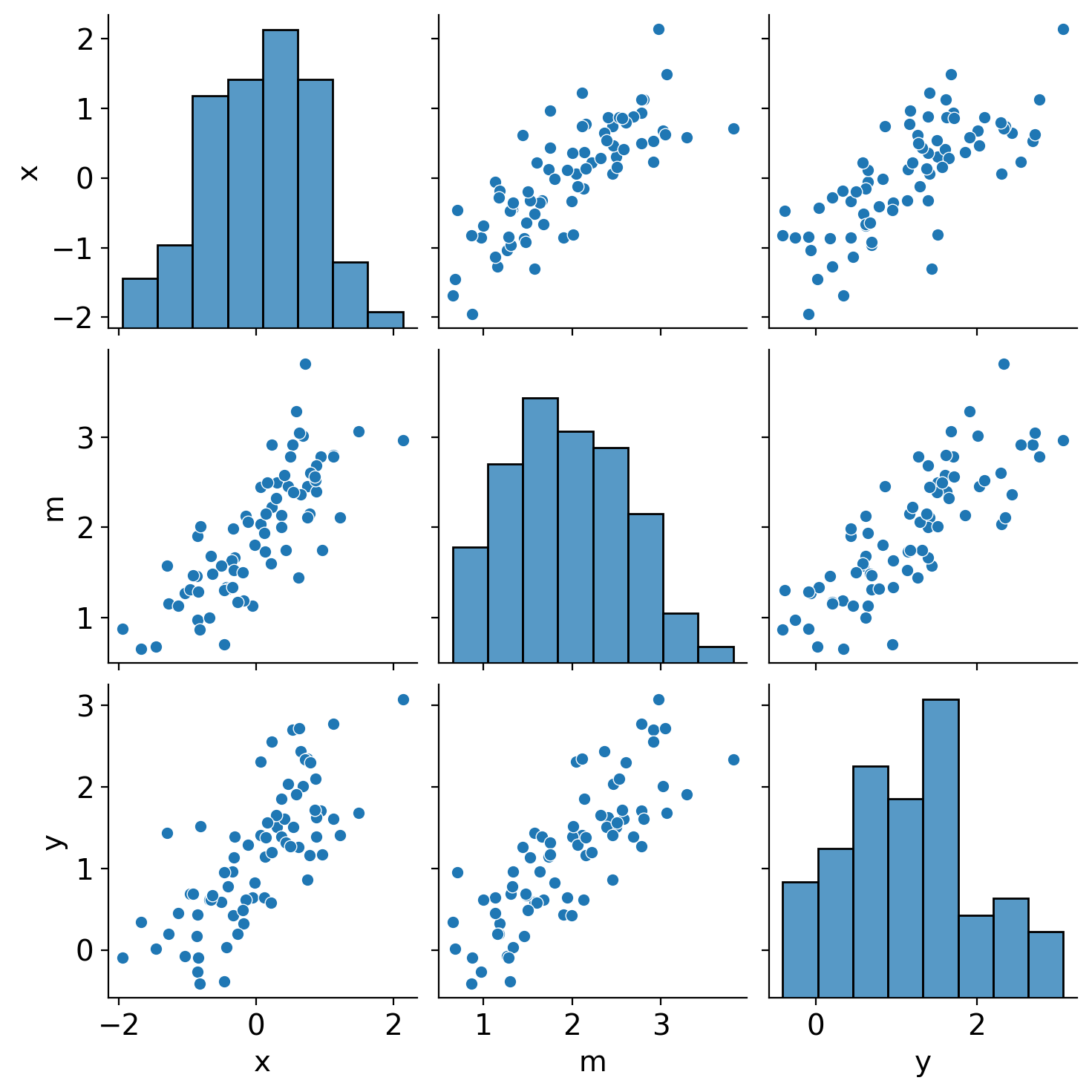
x, m, y = make_data()
sns.pairplot(DataFrame({"x": x, "m": m, "y": y}));
True direct effect = 0.3
True indirect effect = 0.3
True total effect = 0.6
定义 PyMC 模型并进行推理#
def mediation_model(x, m, y):
with pm.Model() as model:
x = pm.ConstantData("x", x, dims="obs_id")
y = pm.ConstantData("y", y, dims="obs_id")
m = pm.ConstantData("m", m, dims="obs_id")
# intercept priors
im = pm.Normal("im", mu=0, sigma=10)
iy = pm.Normal("iy", mu=0, sigma=10)
# slope priors
a = pm.Normal("a", mu=0, sigma=10)
b = pm.Normal("b", mu=0, sigma=10)
cprime = pm.Normal("cprime", mu=0, sigma=10)
# noise priors
σm = pm.HalfCauchy("σm", 1)
σy = pm.HalfCauchy("σy", 1)
# likelihood
pm.Normal("m_likelihood", mu=im + a * x, sigma=σm, observed=m, dims="obs_id")
pm.Normal("y_likelihood", mu=iy + b * m + cprime * x, sigma=σy, observed=y, dims="obs_id")
# calculate quantities of interest
indirect_effect = pm.Deterministic("indirect effect", a * b)
total_effect = pm.Deterministic("total effect", a * b + cprime)
return model
model = mediation_model(x, m, y)
pm.model_to_graphviz(model)
with model:
result = pm.sample(tune=4000, target_accept=0.9, random_seed=42)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [im, iy, a, b, cprime, σm, σy]
Sampling 4 chains for 4_000 tune and 1_000 draw iterations (16_000 + 4_000 draws total) took 9 seconds.
可视化轨迹以检查收敛性。
az.plot_trace(result)
plt.tight_layout()
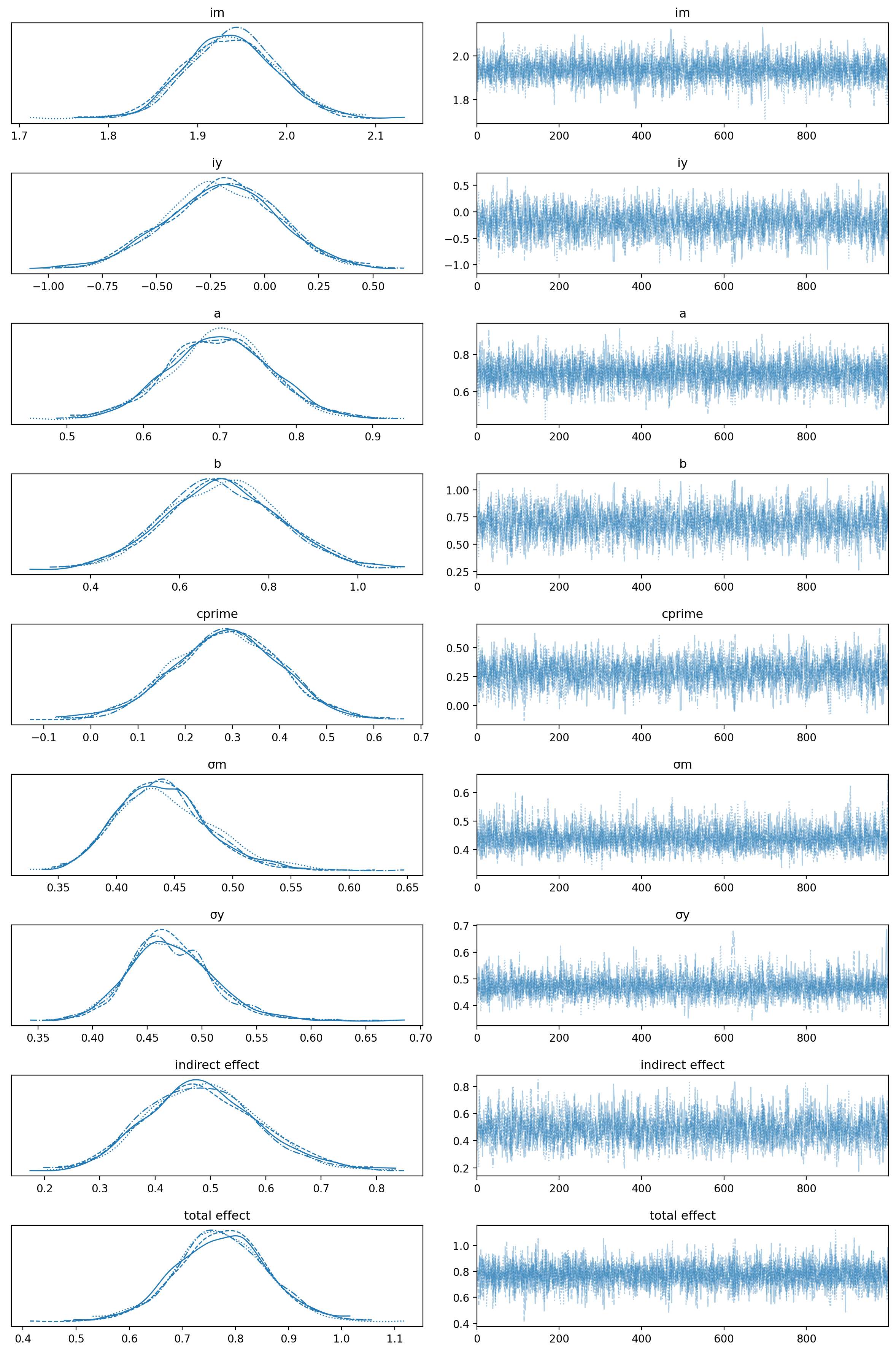
我们拥有良好的链混合,每个链的后验分布看起来非常相似,因此在这方面没有问题。
可视化重要参数#
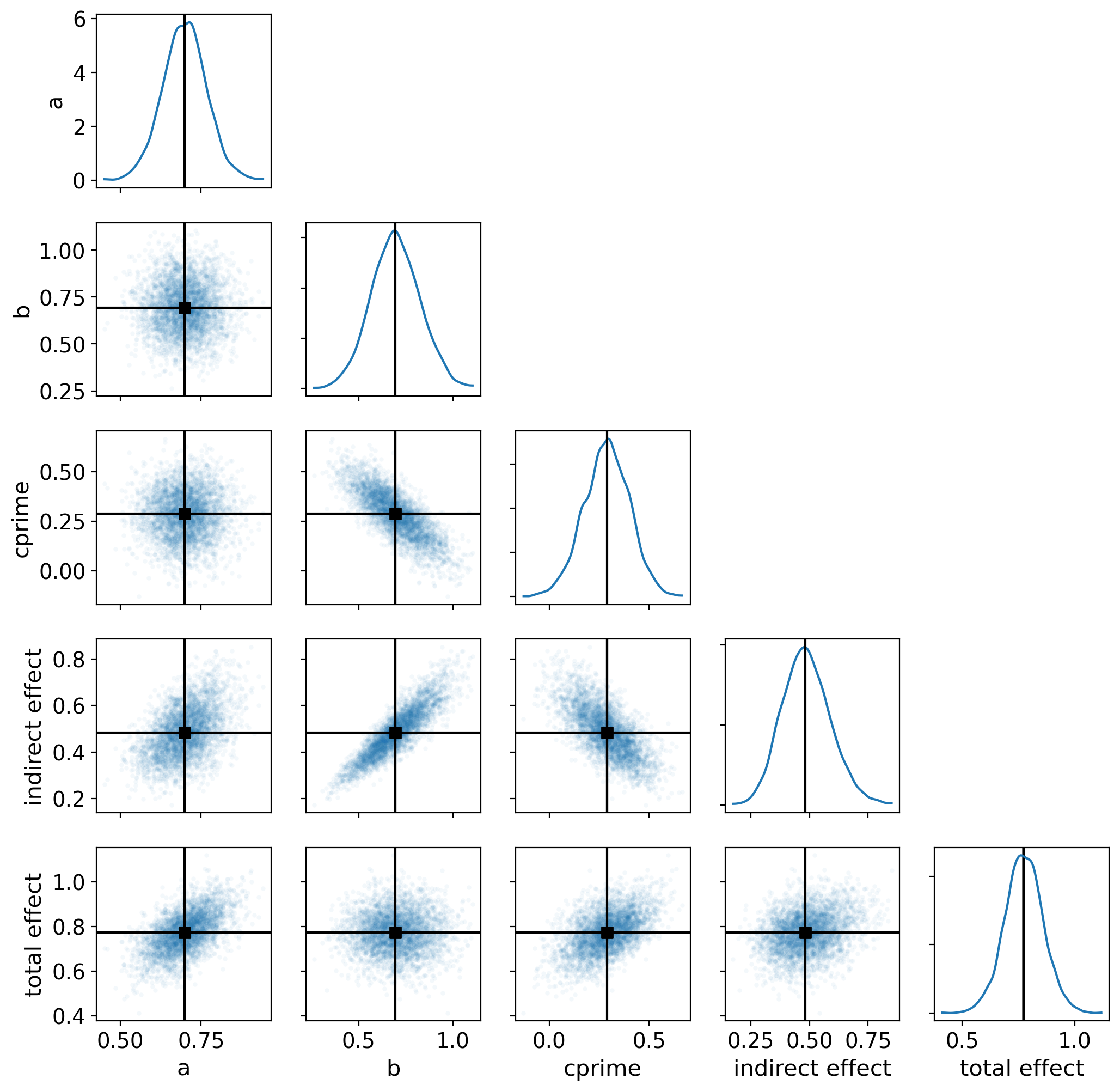
首先我们将使用配对图来查看联合后验分布。
az.plot_pair(
result,
marginals=True,
point_estimate="median",
figsize=(12, 12),
scatter_kwargs={"alpha": 0.05},
var_names=["a", "b", "cprime", "indirect effect", "total effect"],
);
解释结果#
我们可以更仔细地查看间接、总体和直接效应:
ax = az.plot_posterior(
result,
var_names=["cprime", "indirect effect", "total effect"],
ref_val=0,
hdi_prob=0.95,
figsize=(14, 4),
)
ax[0].set(title="direct effect");
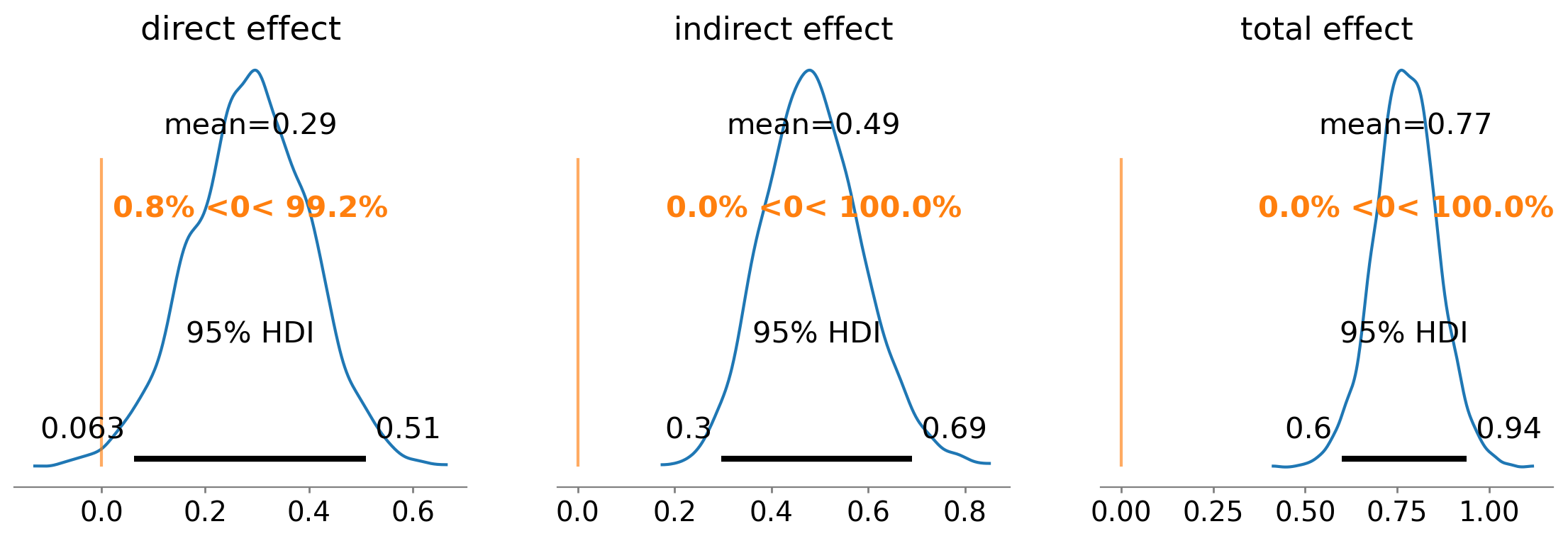
后验均值直接效应为0.29,意味着每增加1单位\(x\),\(y\)由于直接效应\(x \rightarrow y\)增加0.29。
后验均值间接效应为0.49,意味着对于\(x\)每增加1个单位,\(y\)通过路径\(x \rightarrow m \rightarrow y\)增加0.49。间接效应为零的概率是微乎其微的。
后验均值总效应为0.77,意味着每增加1单位\(x\),\(y\)通过直接和间接路径增加0.77。
仅使用总效应模型进行双重检查#
上面,我们提到总效应也可以通过评估替代模型 \(y_i \sim \mathrm{Normal}(i_{Y*} + c \cdot x_i, \sigma_{Y*})\) 来估计。这里我们将通过比较中介模型中 \(c'\) 的后验分布与替代模型中 \(c\) 的后验分布来验证这一点。
with total_effect_model:
total_effect_result = pm.sample(tune=4000, target_accept=0.9, random_seed=42)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [iy, c, σy]
Sampling 4 chains for 4_000 tune and 1_000 draw iterations (16_000 + 4_000 draws total) took 2 seconds.
fig, ax = plt.subplots(figsize=(14, 4))
az.plot_posterior(
total_effect_result, var_names=["c"], point_estimate=None, hdi_prob="hide", c="r", lw=4, ax=ax
)
az.plot_posterior(
result, var_names=["total effect"], point_estimate=None, hdi_prob="hide", c="k", lw=4, ax=ax
);
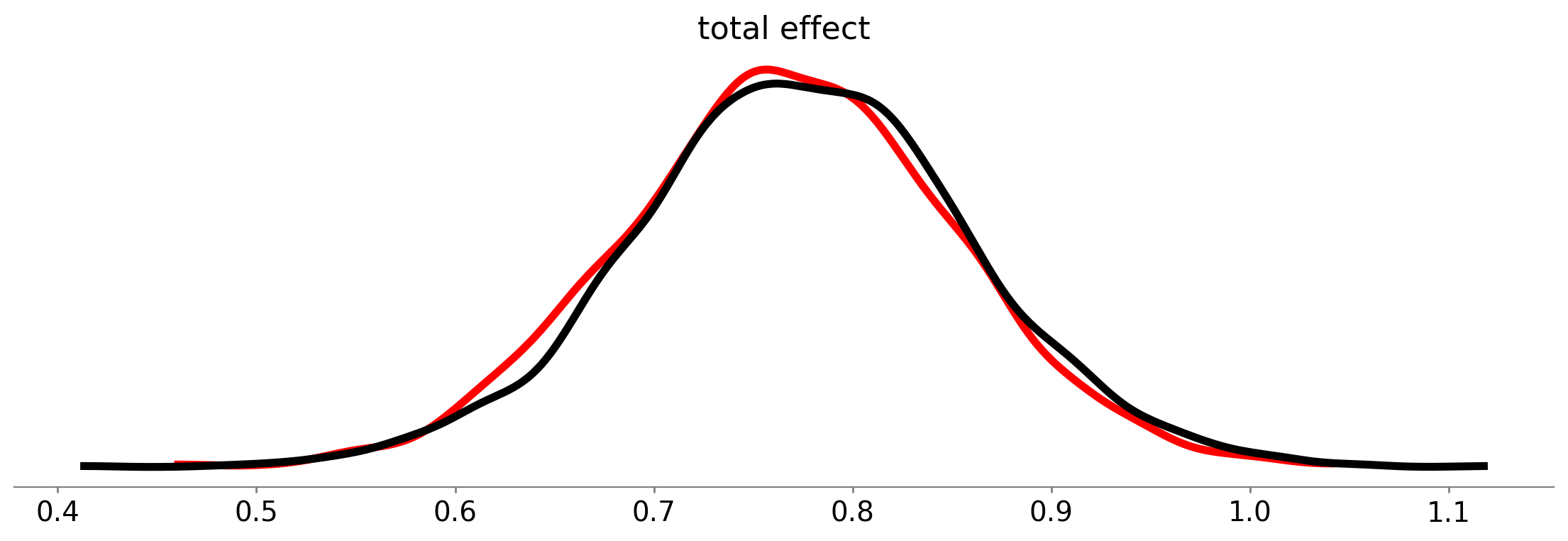
正如我们所见,中介模型(黑色曲线)和直接模型(红色曲线)的直接效应的后验分布几乎是相同的。
参数估计与假设检验#
本笔记本重点介绍了贝叶斯参数估计的方法。在许多情况下,这种方法是完全足够的,更多信息可以在Yuan和MacKinnon [2009]中找到。它将告诉我们,除其他事项外,我们对直接效应、间接效应和总效应的后验信念是什么。我们可以使用这些后验信念来进行后验预测检查,以直观地检查模型对数据的解释程度。
然而,根据使用情况,可能更倾向于测试关于间接效应存在或不存在的假设(例如\(x \rightarrow m \rightarrow y\))。在这种情况下,采用更明确的假设检验方法来检查与简单直接效应模型(即\(y_i = \mathrm{Normal}(i_{Y*} + c \cdot x_i, \sigma_{Y*})\))相比,中介模型的相对可信度可能更为合适。读者可参考Nuijten 等人 [2015]了解贝叶斯中介模型的假设检验方法,并参考Kruschke [2011]获取更多关于参数估计与假设检验的信息。
概述#
如开头所述,调解分析中使用的方法已经随着时间的推移而发展。因此,有很多人不一定了解现代的最佳实践。本笔记本中的方法遵循了Hayes [2017]所概述的内容,但了解一些历史背景以避免混淆是相关的——这在同行评审中为自己的方法辩护时尤为重要。
参考资料#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl,xarray
Last updated: Wed Feb 01 2023
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.9.0
pytensor: 2.8.11
aeppl : not installed
xarray : 2023.1.0
arviz : 0.14.0
pymc : 5.0.1
matplotlib: 3.6.3
numpy : 1.24.1
seaborn : 0.12.2
Watermark: 2.3.1
许可证声明#
本示例库中的所有笔记本均在MIT许可证下提供,该许可证允许修改和重新分发,前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本,请使用Zenodo为pymc-examples仓库提供的DOI。
重要
许多笔记本是从其他来源改编的:博客、书籍……在这种情况下,您应该引用原始来源。
同时记得引用代码中使用的相关库。
这是一个BibTeX的引用模板:
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像: