GP-Circular#

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm
import theano.tensor as tt

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")

圆形域对于高斯过程来说是一个挑战。

  • 假设存在周期性模式，但它们很难用基本元素捕捉

  • 对于圆形域 \([0, \pi)\) 如何建模 \(\pi-\varepsilon\) 和 \(\varepsilon\) 之间的相关性，实际距离是 \(2\varepsilon\)，但如果您只是将其视为非圆形 \((\pi-\varepsilon) - \varepsilon\)，则计算方式不同。

  • 为了正确计算距离，我们需要验证所得到的核函数是正定的

需要采用另一种方法。

在以下论文中，Weinland函数被用于解决问题，并确保在圆形域（以及不仅仅是）上的正定核。

\[ W_c(t) = \left(1 + \tau \frac{t}{c}\right)\left(1-\frac{t}{c}\right)_+^\tau \]

其中 \(c\) 是 \(t\) 的最大值，而 \(\tau\ge 4\) 是某个正数

用于计算圆上测地距离（弧长）的内核本身看起来像

\[ k_g(x, y) = W_\pi(\text{dist}_{\mathit{geo}}(x, y)) \]

简而言之，你可以认为

  • \(t\) 是时间，它从 \(0\) 运行到 \(24\)，然后回到 \(0\)

  • \(c\) 是任意时间戳之间的最大距离，这里将是 \(12\)

  • \(\tau\) 与相关强度成正比。让我们看看有多少！

在Python中，Weinland函数是这样实现的

def weinland(t, c, tau=4):
    return (1 + tau * t / c) * np.clip(1 - t / c, 0, np.inf) ** tau

我们还需要实现圆形域上的距离计算

def angular_distance(x, y, c):
    # https://stackoverflow.com/questions/1878907/the-smallest-difference-between-2-angles
    return (x - y + c) % (c * 2) - c

C = np.pi
x = np.linspace(0, C)

让我们可视化Weinland函数是什么，以及它如何影响核函数：

plt.figure(figsize=(16, 9))
for tau in range(4, 10):
    plt.plot(x, weinland(x, C, tau), label=f"tau={tau}")
plt.legend()
plt.ylabel("K(x, y)")
plt.xlabel("dist");
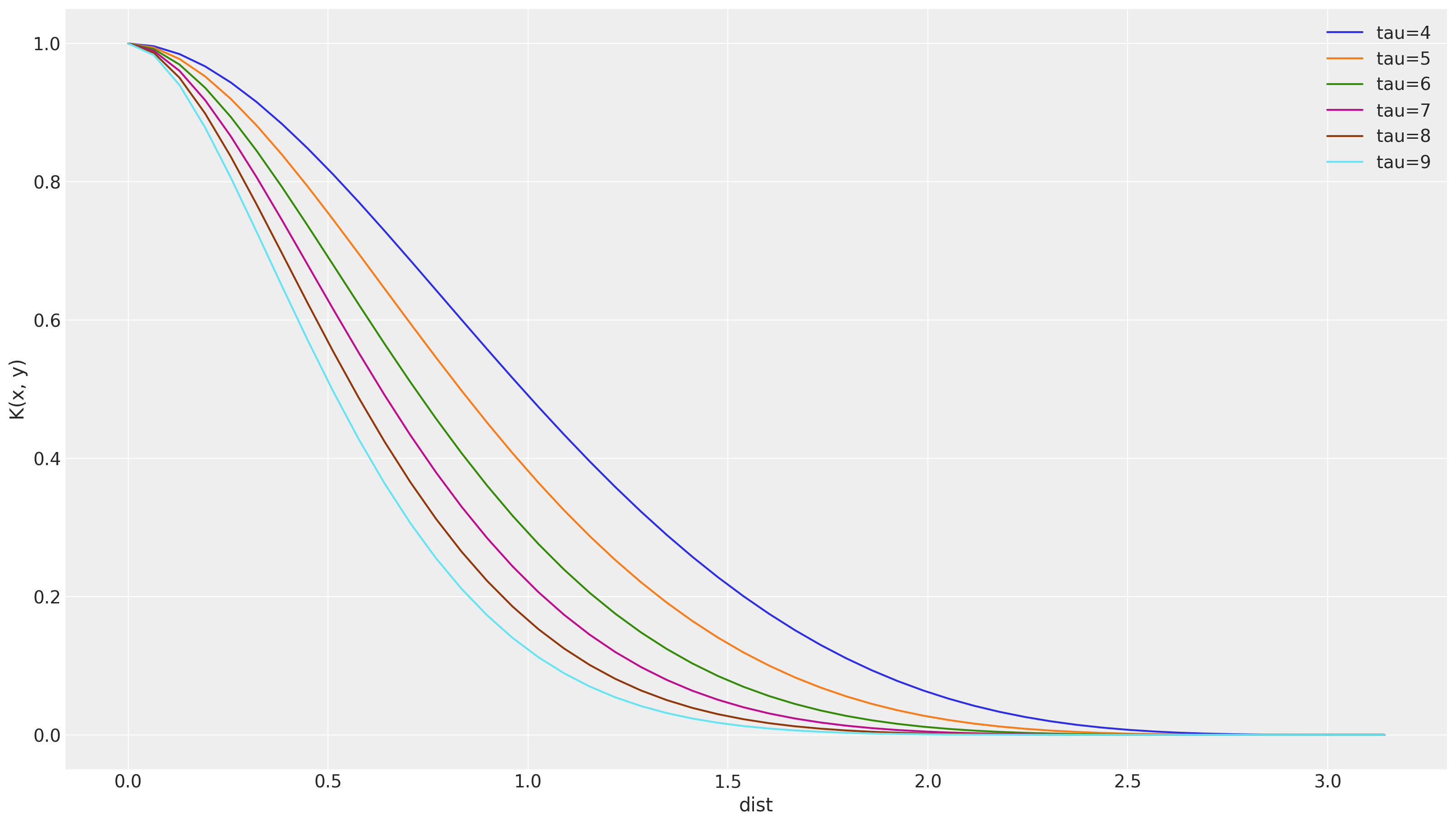
../_images/6d6b411075905d18c7dd9d8a10c79a3a2e2b08203af2daaa4b1f31b355210963.png

正如我们所见，\(\tau\) 越高，样本的相关性越低

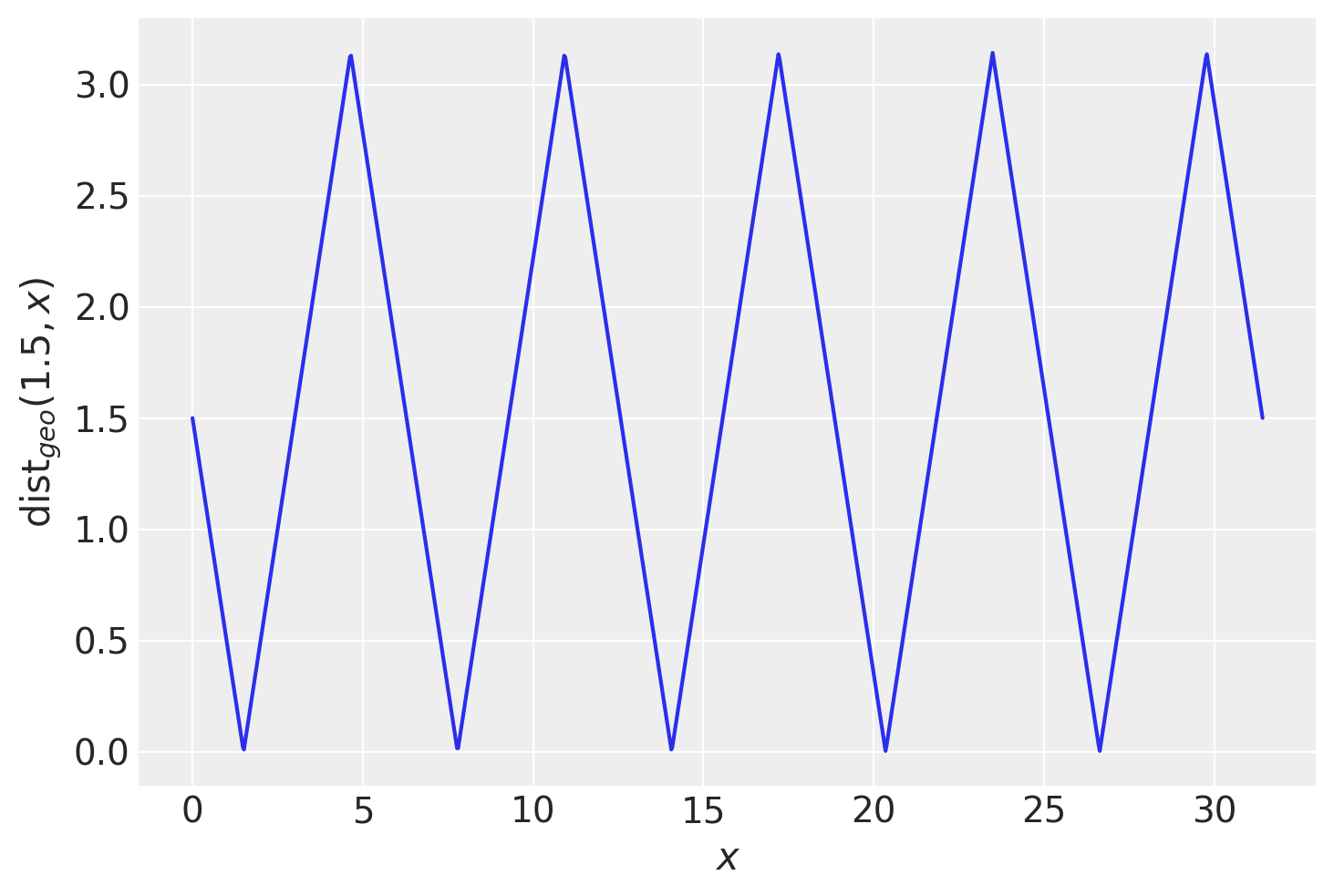
另外，让我们验证一下我们的圆形距离函数是否按预期工作

plt.plot(
    np.linspace(0, 10 * np.pi, 1000),
    abs(angular_distance(np.linspace(0, 10 * np.pi, 1000), 1.5, C)),
)
plt.ylabel(r"$\operatorname{dist}_{geo}(1.5, x)$")
plt.xlabel("$x$");
../_images/2aec53bbd4d1b612593f50aa4e34bf58b0cd262509590422acdec77e0a3e7913.png

在 pymc3 中，我们将使用 pm.gp.cov.Circular 来建模圆形函数

angles = np.linspace(0, 2 * np.pi)
observed = dict(x=np.random.uniform(0, np.pi * 2, size=5), y=np.random.randn(5) + 4)


def plot_kernel_results(Kernel):
    """
    To check for many kernels we leave it as a parameter
    """
    with pm.Model() as model:
        cov = Kernel()
        gp = pm.gp.Marginal(pm.gp.mean.Constant(4), cov_func=cov)
        lik = gp.marginal_likelihood("x_obs", X=observed["x"][:, None], y=observed["y"], noise=0.2)
        mp = pm.find_MAP()
        # actual functions
        y_sampled = gp.conditional("y", angles[:, None])
        # GP predictions (mu, cov)
        y_pred = gp.predict(angles[:, None], point=mp)
        trace = pm.sample_posterior_predictive([mp], var_names=["y"], samples=100)
    plt.figure(figsize=(9, 9))
    paths = plt.polar(angles, trace["y"].T, color="b", alpha=0.05)
    plt.scatter(observed["x"], observed["y"], color="r", alpha=1, label="observations")
    plt.polar(angles, y_pred[0], color="black")
    plt.fill_between(
        angles,
        y_pred[0] - np.diag(y_pred[1]) ** 0.5,
        y_pred[0] + np.diag(y_pred[1]) ** 0.5,
        color="gray",
        alpha=0.5,
        label=r"$\mu\pm\sigma$",
    )
    plt.fill_between(
        angles,
        y_pred[0] - np.diag(y_pred[1]) ** 0.5 * 3,
        y_pred[0] + np.diag(y_pred[1]) ** 0.5 * 3,
        color="gray",
        alpha=0.25,
        label=r"$\mu\pm3\sigma$",
    )
    plt.legend()

def circular():
    tau = pm.Deterministic("τ", pm.Gamma("_τ", alpha=2, beta=1) + 4)
    cov = pm.gp.cov.Circular(1, period=2 * np.pi, tau=tau)
    return cov

plot_kernel_results(circular)
100.00% [7/7 00:00<00:00 logp = -6.9811, ||grad|| = 0.94385]
100.00% [100/100 00:01<00:00]
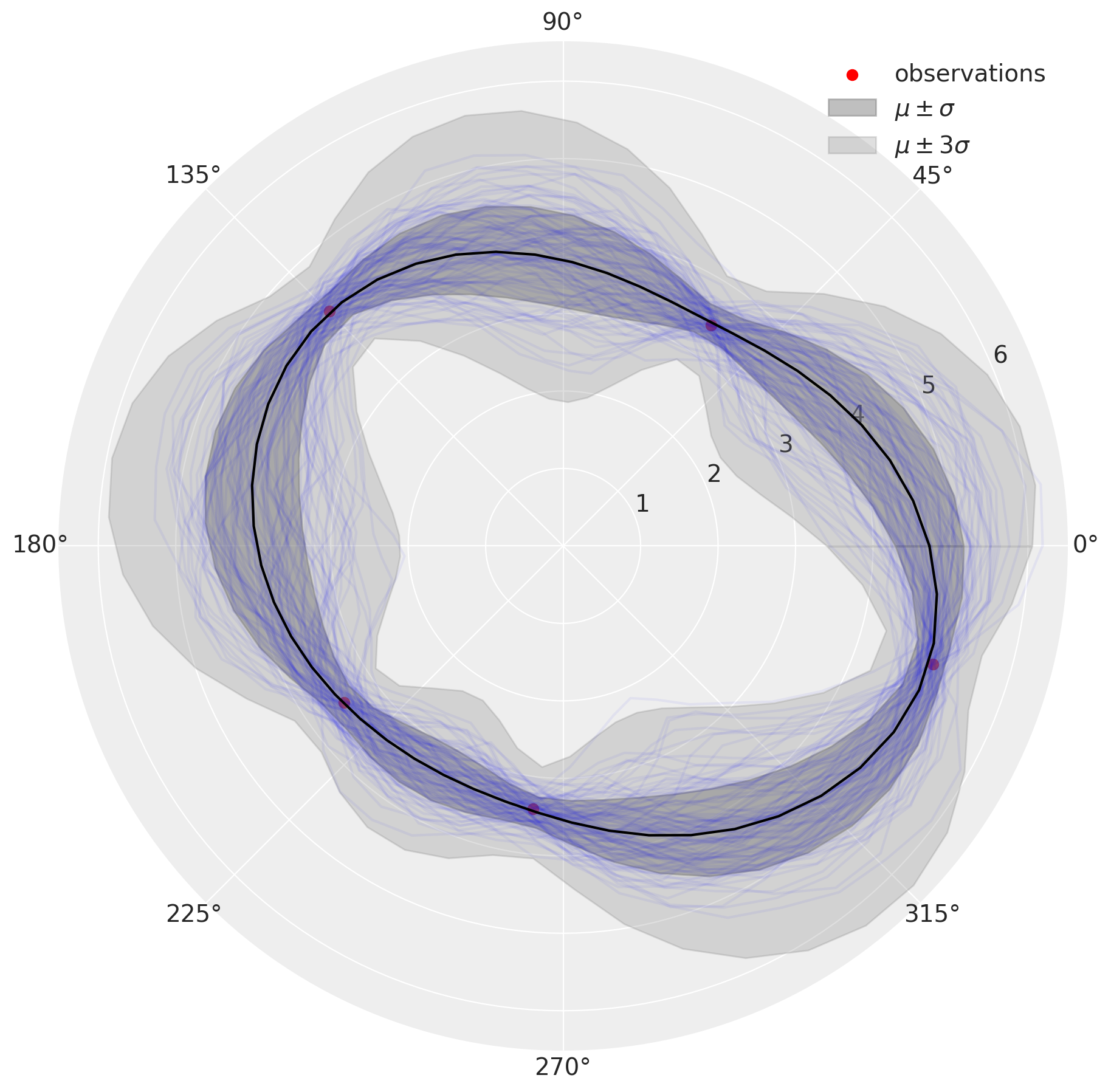
../_images/b85877827819aef038e57510082452001184f305587d8a4e019711cdd10c1373.png

另一种解决方案是周期性核函数。

注意：

  • 在周期性核函数中，控制点之间相关性的关键参数是 ls

  • 在圆形核中，它是tau，添加ls参数没有意义，因为它会相互抵消

基本上，这些核函数之间几乎没有区别，只是建模相关性的方式不同。

def periodic():
    ls = pm.Gamma("ℓ", alpha=2, beta=1)
    return pm.gp.cov.Periodic(1, 2 * np.pi, ls=ls)

plot_kernel_results(periodic)
100.00% [13/13 00:00<00:00 logp = -7.1213, ||grad|| = 0.0066278]
100.00% [100/100 00:00<00:00]
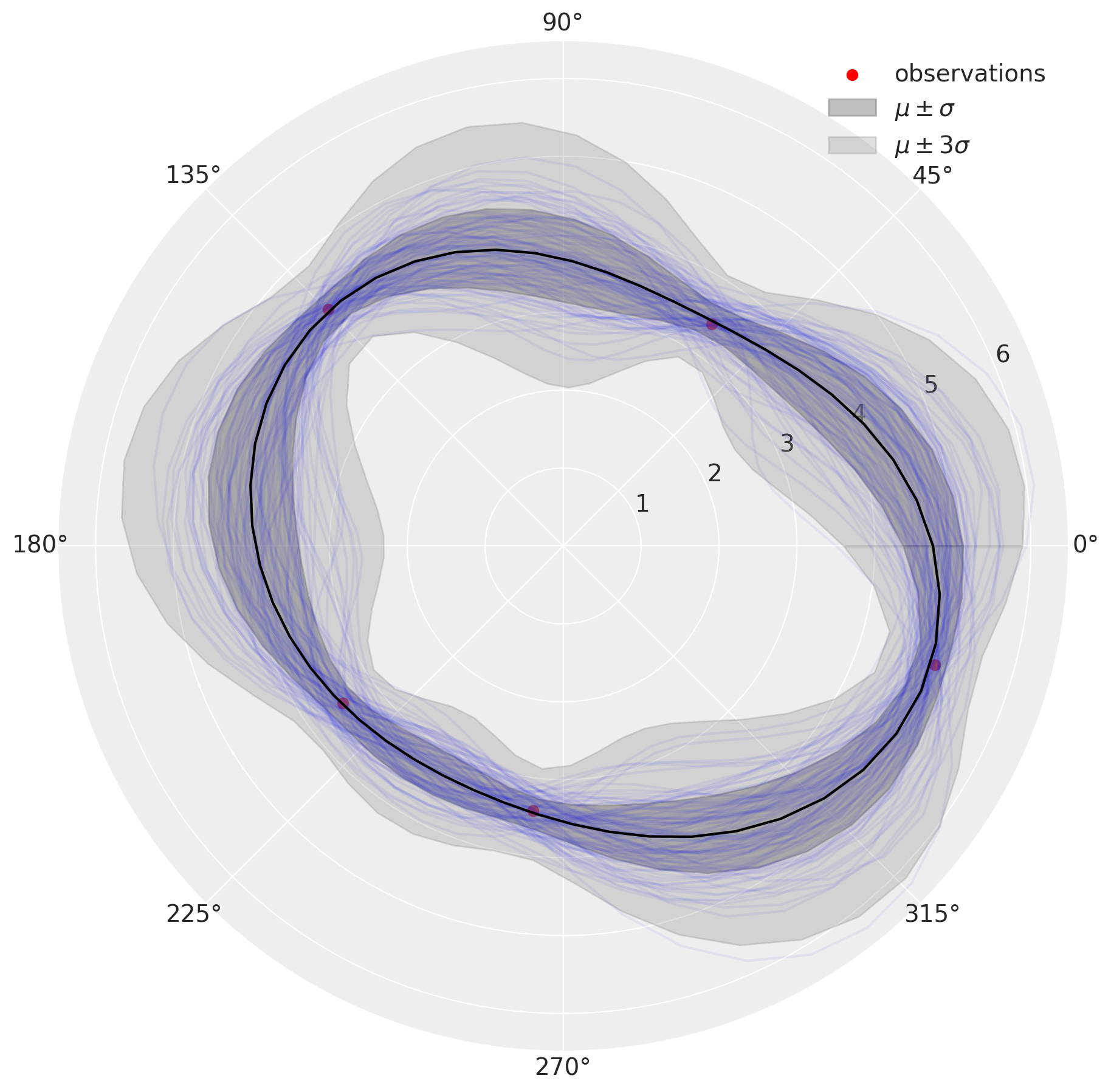
../_images/655c64d6e170506bee4917ce9d72580380c37c1dc9b2ea1302b4c6413563aa18.png

从模拟中，我们看到圆形核导致后验更加不确定。

让我们看看指数核函数是如何失败的

def rbf():
    ls = pm.Gamma("ℓ", alpha=2, beta=1)
    return pm.gp.cov.Exponential(1, ls=ls)

plot_kernel_results(rbf)
100.00% [6/6 00:00<00:00 logp = -7.4099, ||grad|| = 1.8782]
100.00% [100/100 00:01<00:00]
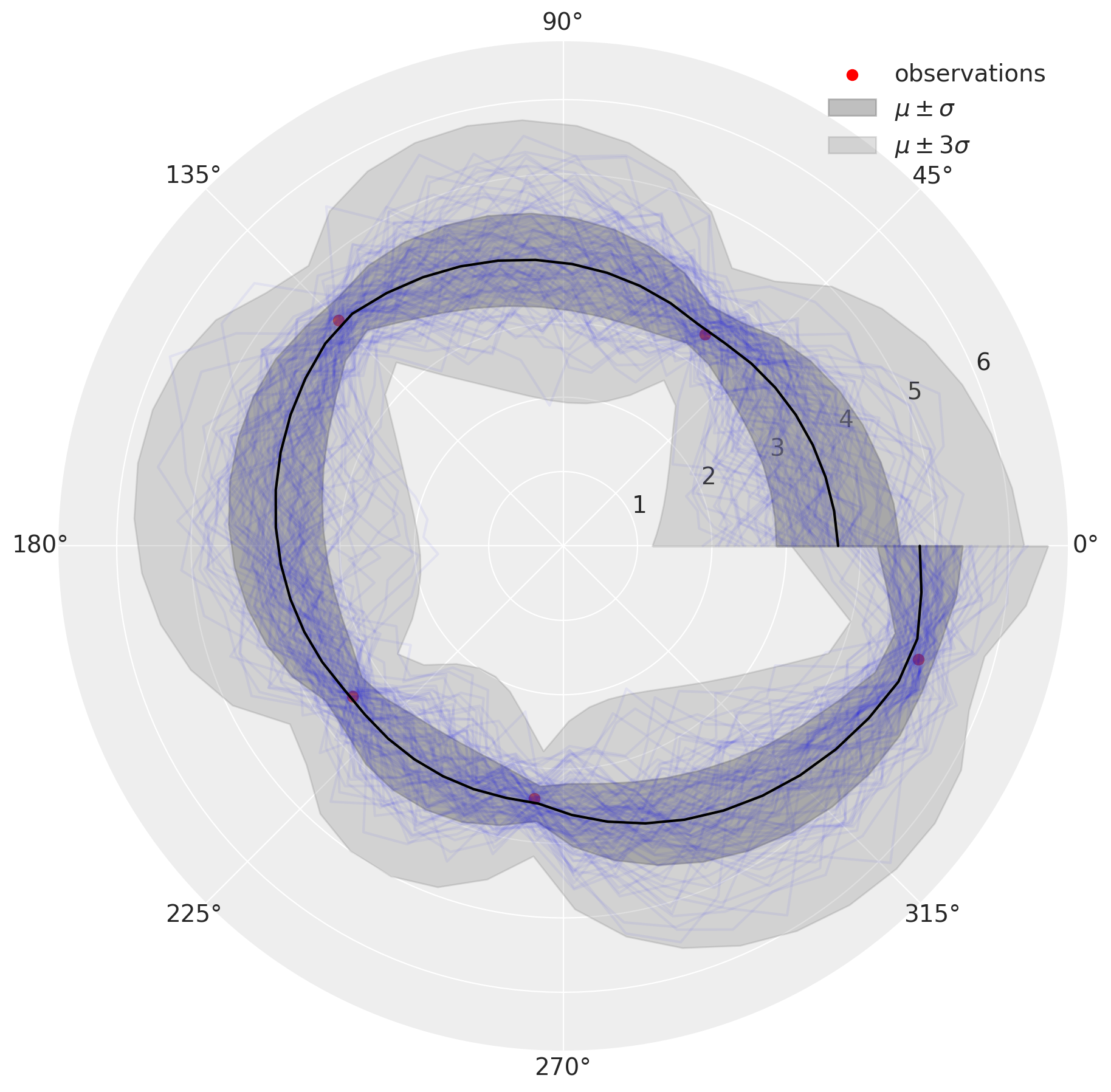
../_images/17b5ed0d51d8b2455a4411ce792c41a696fabd8872cda69392f0c4fa184cd9bb.png

结果看起来与我们使用圆形核函数时的结果相似，但变化点\(0^\circ\)未被考虑在内

结论#

  • 当你强烈认为函数应该平滑地通过周期的边界时，使用循环/周期性核函数

  • 周期核与圆形核一样精细，只是后者允许更多的不确定性

  • RBF 核函数不是正确的选择

%load_ext watermark
%watermark -n -u -v -iv -w

pymc3 3.9.3
numpy 1.19.0
arviz 0.9.0
last updated: Sat Oct 10 2020 

CPython 3.8.6
IPython 7.17.0
watermark 2.0.2