高斯过程 (GP) 平滑#
这个例子处理了我们想要对观测到的数据点 \((x_i, y_i)\) 进行平滑处理的情况,这些数据点来自某个一维函数 \(y=f(x)\)。通过找到新的值 \((x_i, y'_i)\),使得在沿着 \(x\) 轴移动时,新的数据更加“平滑”(关于平滑度的定义,请参阅下面的模型描述中通过分配方差的部分)。
需要注意的是,我们不处理在未知值\(x\)处插值函数\(y=f(x)\)的问题。这样的问题将被称为“回归”而不是“平滑”,并将在其他示例中进行考虑。
如果我们假设\(x\)和\(y\)之间的函数依赖关系是线性的,那么通过假设噪声的独立性和正态性,我们可以推断出一条近似变量之间依赖关系的直线,即进行线性回归。如果我们事先知道依赖关系的函数形式,我们也可以拟合更复杂的函数依赖关系(如二次、三次等)。
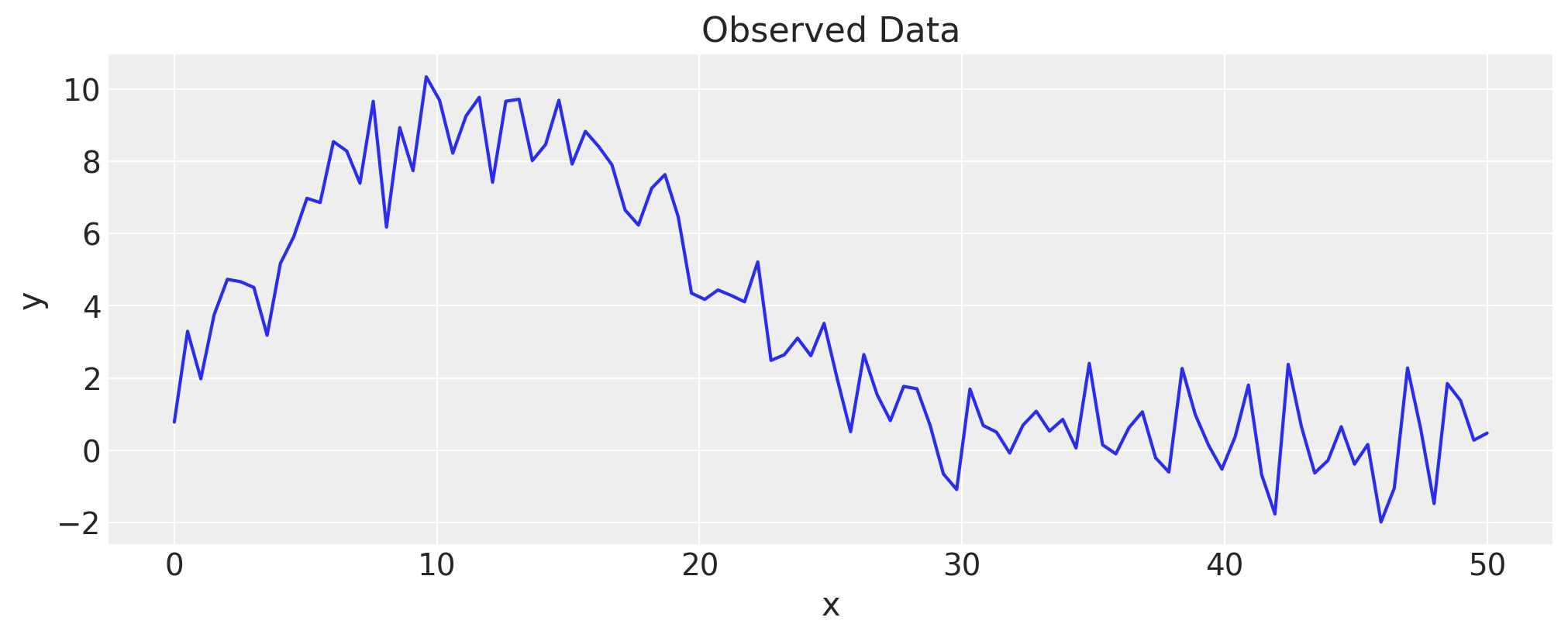
然而,函数形式 \(y=f(x)\) 并不总是事先已知的,并且在给定数据的情况下,可能很难选择要拟合的函数。例如,在给定以下观测数据的情况下,您不一定知道要使用哪个函数。假设您还没有看到生成它的公式:
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import scipy.stats as stats
from pytensor import shared
%config InlineBackend.figure_format = "retina"
WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
plt.rcParams["figure.figsize"] = (10, 4)
x = np.linspace(0, 50, 100)
y = np.exp(1.0 + np.power(x, 0.5) - np.exp(x / 15.0)) + rng.normal(scale=1.0, size=x.shape)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.set(title="Observed Data", xlabel="x", ylabel="y");
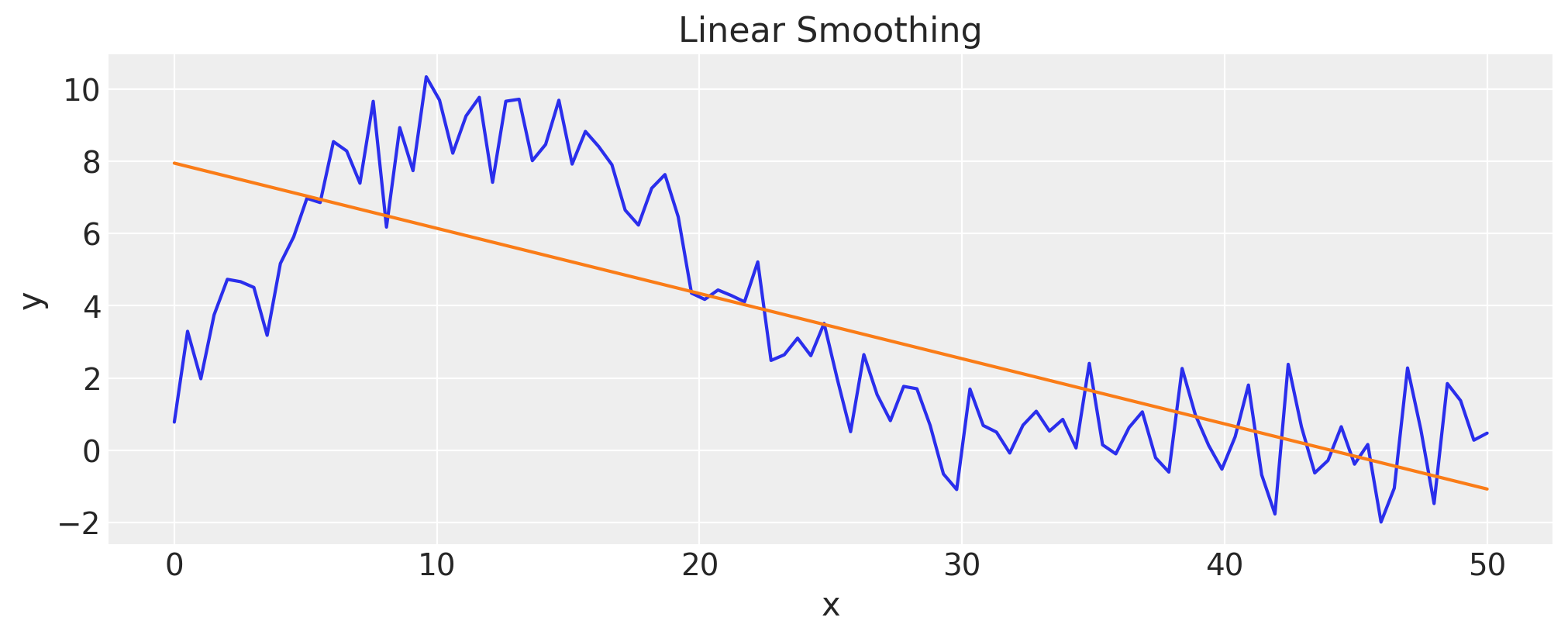
让我们先尝试一个线性回归#
作为人类,我们观察到存在一些噪声的非线性依赖关系,我们希望捕捉到这种依赖关系。如果我们进行线性回归,我们会发现“平滑”后的数据并不令人满意:
lin = stats.linregress(x, y)
fig, ax = plt.subplots()
ax.plot(x, y)
lin = stats.linregress(x, y)
ax.plot(x, lin.intercept + lin.slope * x)
ax.set(title="Linear Smoothing", xlabel="x", ylabel="y");
线性回归模型回顾#
线性回归假设输入\(x\)和输出\(y\)之间存在线性依赖关系,并伴随一些噪声,因此对于每个观察到的数据点,我们有:
其中每个数据点的观测误差满足:
具有相同的\(\sigma\),并且误差是独立的:
该模型的参数是 \(a\), \(b\), 和 \(\sigma\)。事实证明,在这些假设下,\(a\) 和 \(b\) 的最大似然估计值不依赖于 \(\sigma\)。然后可以在找到 \(a\) 和 \(b\) 的最可能值之后,单独估计 \(\sigma\)。
高斯过程平滑模型#
该模型通过假设\(x\)和\(y\)之间的依赖关系在\(x\)的域上是布朗运动,从而允许偏离线性依赖。这并不像假设变量之间的特定函数依赖那样极端。相反,通过控制未观察到的布朗运动的标准差,我们可以在原始数据点上实现恢复的函数依赖的不同平滑度水平。
我们即将讨论的特定模型假设观测数据点在\(x\)的定义域上是均匀分布的,因此可以不失一般性地通过\(i=1,\dots,N\)进行索引。该模型描述如下:
其中 \(z\) 是隐藏的布朗运动,\(y\) 是观测数据,每个观测值的总方差 \(\sigma^2\) 在隐藏的布朗运动和噪声之间按比例 \(1 - \alpha\) 和 \(\alpha\) 分配,参数 \(0 < \alpha < 1\) 指定平滑程度。
当我们估计每个数据点上隐藏过程 \(z_i\) 的最大似然值时,\(i=1,\dots,N\),这些值在原始数据点 \(x_i\) 上提供了函数依赖 \(y=f(x)\) 的近似值,即 \(\mathrm{E}\,[f(x_i)] = z_i\)。因此,再次强调,该方法称为平滑而非回归。
让我们在PyMC中描述上述GP平滑模型#
让我们创建一个具有共享参数的模型,用于指定不同的平滑级别。我们对隐藏布朗运动的“mu”和“tau”参数使用非常宽的先验,您可以根据您的应用进行调整。
LARGE_NUMBER = 1e5
model = pm.Model()
with model:
smoothing_param = shared(0.9)
mu = pm.Normal("mu", sigma=LARGE_NUMBER)
tau = pm.Exponential("tau", 1.0 / LARGE_NUMBER)
z = pm.GaussianRandomWalk(
"z", mu=mu, sigma=pm.math.sqrt((1.0 - smoothing_param) / tau), shape=y.shape
)
obs = pm.Normal("obs", mu=z, tau=tau / smoothing_param, observed=y)
/Users/juanitorduz/anaconda3/envs/pymc-examples-env/lib/python3.11/site-packages/pymc/distributions/timeseries.py:293: UserWarning: Initial distribution not specified, defaulting to `Normal.dist(0, 100)`.You can specify an init_dist manually to suppress this warning.
warnings.warn(
让我们也创建一个辅助函数来推断\(z\)的最可能值:
def infer_z(smoothing):
with model:
smoothing_param.set_value(smoothing)
res = pm.find_MAP(vars=[z], method="L-BFGS-B")
return res["z"]
请注意,在这个示例中,我们只关注未观测变量的最大后验估计(MAP estimate)。我们并不真正关心推断后验分布。相反,我们有一个控制参数 \(\alpha\),它让我们可以在隐藏的布朗运动和噪声之间分配方差。其他目标或不同的模型可能需要采样来获得后验分布,但对于我们的目标,最大后验估计已经足够。
探索不同的平滑级别#
让我们尝试将50%的方差分配给噪声,看看结果是否符合我们的预期。
smoothing = 0.5
z_val = infer_z(smoothing)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(x, z_val)
ax.set(title=f"Smoothing={smoothing}");
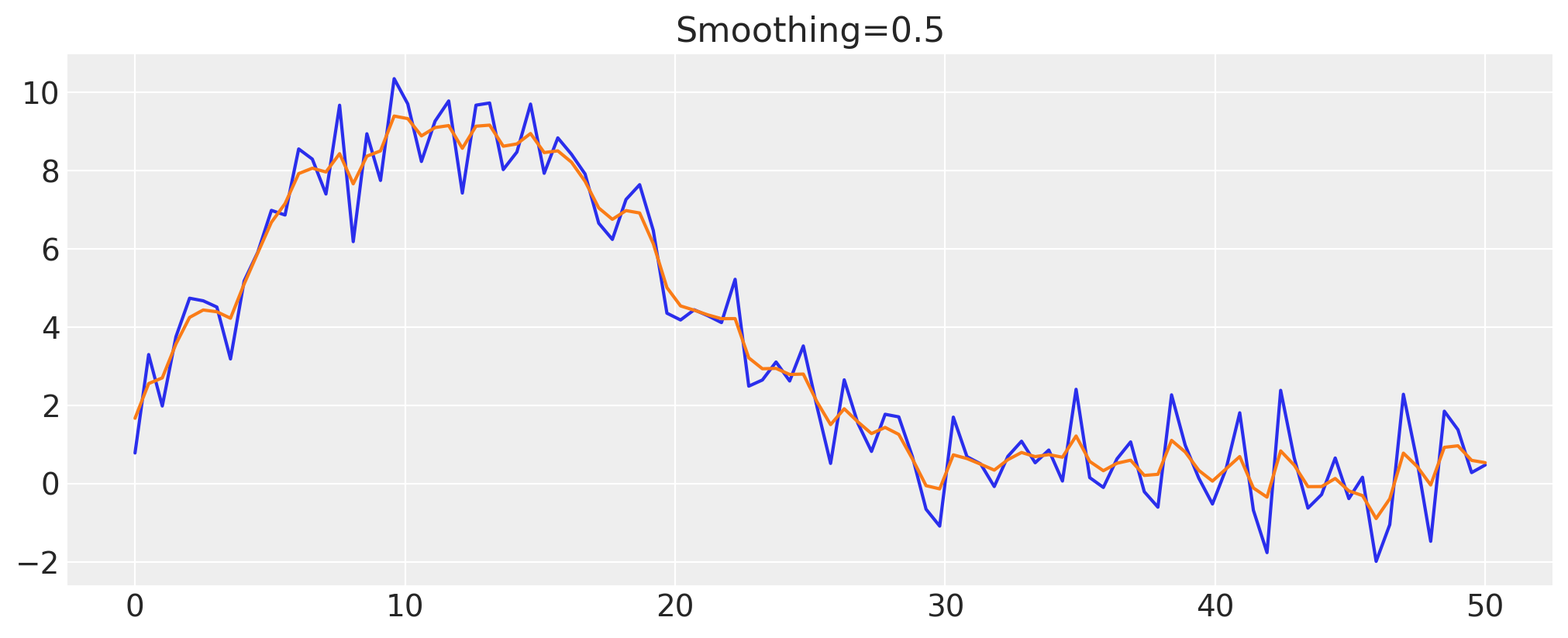
看起来方差在噪声和隐藏过程之间均匀分配,正如预期的那样。
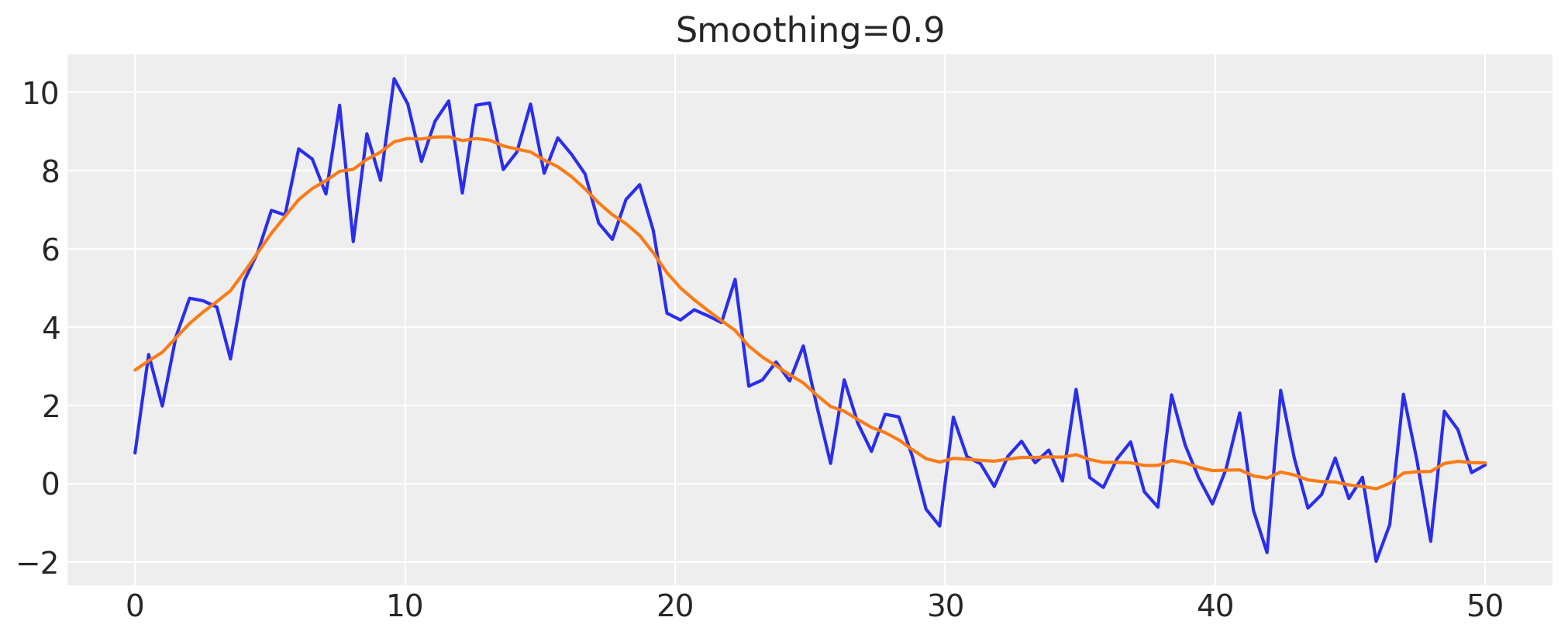
让我们尝试逐渐增加平滑度参数,看看是否能获得更平滑的数据:
smoothing = 0.9
z_val = infer_z(smoothing)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(x, z_val)
ax.set(title=f"Smoothing={smoothing}");
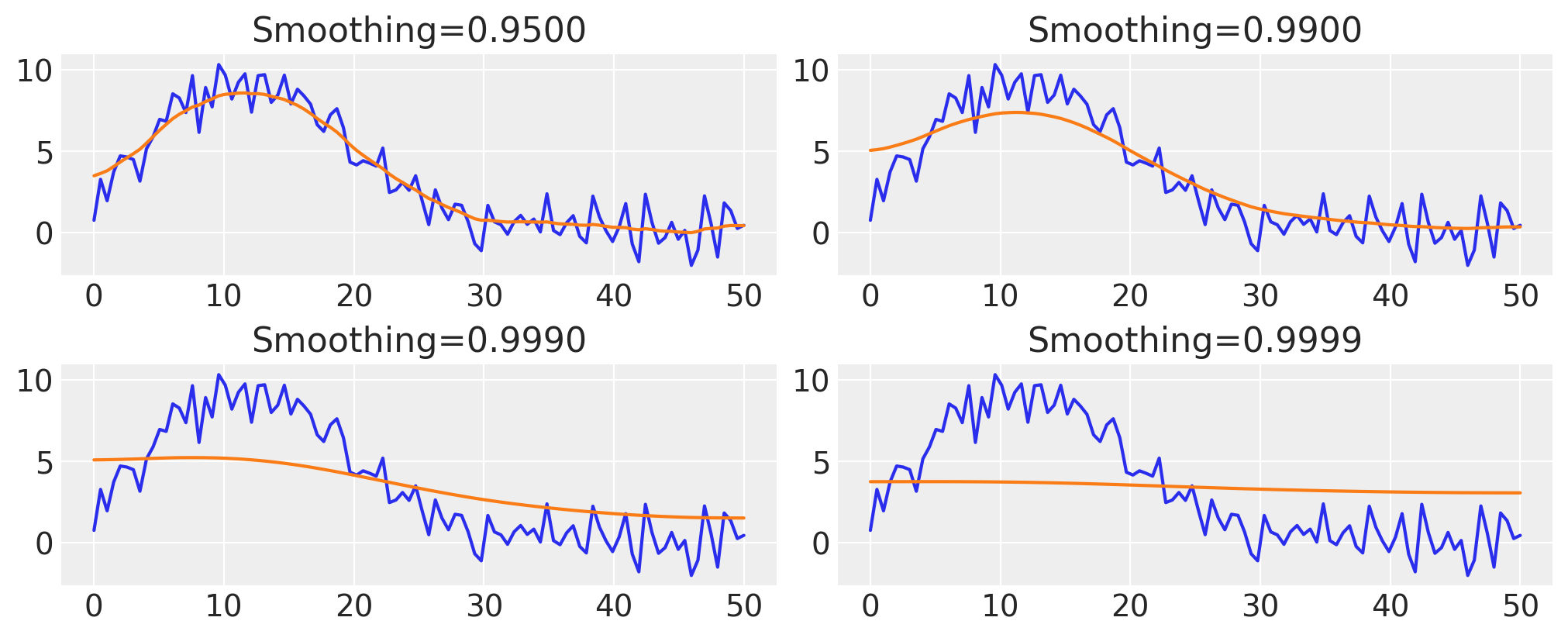
平滑“到极限”#
通过增加平滑参数,我们可以逐渐使隐藏的布朗运动推断值接近数据的平均值。这是因为随着我们增加平滑参数,我们允许分配给布朗运动的方差越来越少,因此最终它接近于在\(x\)域上几乎不变化的过程:
fig, axes = plt.subplots(nrows=2, ncols=2)
for ax, smoothing in zip(axes.ravel(), [0.95, 0.99, 0.999, 0.9999]):
z_val = infer_z(smoothing)
ax.plot(x, y)
ax.plot(x, z_val)
ax.set_title(f"Smoothing={smoothing:05.4f}")