GLM: 模型选择#
import arviz as az
import bambi as bmb
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import seaborn as sns
import xarray as xr
from ipywidgets import fixed, interactive
print(f"Running on PyMC3 v{pm.__version__}")
Running on PyMC3 v3.11.4
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
plt.rcParams["figure.constrained_layout.use"] = False
介绍#
一个相当简洁的可重复模型选择示例，使用WAIC和LOO，如当前在PyMC3中实现的那样。
此示例在线性和二次模型下创建了两个玩具数据集，然后使用广泛适用信息准则（WAIC）和使用Pareto平滑重要性采样（PSIS）的留一法（LOO）交叉验证来测试一系列多项式线性模型在这些数据集上的拟合情况。
该示例灵感来源于Jake Vanderplas关于模型选择的博客文章，尽管未实现交叉验证和贝叶斯因子比较。数据集非常小，并在本Notebook中生成。它们仅在测量值（y）中包含误差。
本地函数#
我们开始编写一些函数来帮助完成笔记本的其他部分。只有一些函数对于理解笔记本至关重要，其余的函数是为了在需要时使绘图更加简洁的便利函数，并且隐藏在一个可切换的部分中；它仍然可用，但您需要点击才能看到它。
def generate_data(n=20, p=0, a=1, b=1, c=0, latent_sigma_y=20, seed=5):
"""
Create a toy dataset based on a very simple model that we might
imagine is a noisy physical process:
1. random x values within a range
2. latent error aka inherent noise in y
3. optionally create labelled outliers with larger noise
Model form: y ~ a + bx + cx^2 + e
NOTE: latent_sigma_y is used to create a normally distributed,
'latent error' aka 'inherent noise' in the 'physical' generating
process, rather than experimental measurement error.
Please don't use the returned `latent_error` values in inferential
models, it's returned in the dataframe for interest only.
"""
rng = np.random.default_rng(seed)
df = pd.DataFrame({"x": rng.choice(np.arange(100), n, replace=False)})
# create linear or quadratic model
df["y"] = a + b * (df["x"]) + c * (df["x"]) ** 2
# create latent noise and marked outliers
df["latent_error"] = rng.normal(0, latent_sigma_y, n)
df["outlier_error"] = rng.normal(0, latent_sigma_y * 10, n)
df["outlier"] = rng.binomial(1, p, n)
# add noise, with extreme noise for marked outliers
df["y"] += (1 - df["outlier"]) * df["latent_error"]
df["y"] += df["outlier"] * df["outlier_error"]
# round
for col in ["y", "latent_error", "outlier_error", "x"]:
df[col] = np.round(df[col], 3)
# add label
df["source"] = "linear" if c == 0 else "quadratic"
# create simple linspace for plotting true model
plotx = np.linspace(
df["x"].min() - np.ptp(df["x"].values) * 0.1,
df["x"].max() + np.ptp(df["x"].values) * 0.1,
100,
)
ploty = a + b * plotx + c * plotx**2
dfp = pd.DataFrame({"x": plotx, "y": ploty})
return df, dfp
Show code cell content
def interact_dataset(n=20, p=0, a=-30, b=5, c=0, latent_sigma_y=20):
"""
Convenience function:
Interactively generate dataset and plot
"""
df, dfp = generate_data(n, p, a, b, c, latent_sigma_y)
g = sns.FacetGrid(
df,
height=8,
hue="outlier",
hue_order=[True, False],
palette=sns.color_palette("bone"),
legend_out=False,
)
g.map(
plt.errorbar,
"x",
"y",
"latent_error",
marker="o",
ms=10,
mec="w",
mew=2,
ls="",
elinewidth=0.7,
).add_legend()
plt.plot(dfp["x"], dfp["y"], "--", alpha=0.8)
plt.subplots_adjust(top=0.92)
g.fig.suptitle("Sketch of Data Generation ({})".format(df["source"][0]), fontsize=16)
def plot_datasets(df_lin, df_quad, dfp_lin, dfp_quad):
"""
Convenience function:
Plot the two generated datasets in facets with generative model
"""
df = pd.concat((df_lin, df_quad), axis=0)
g = sns.FacetGrid(col="source", hue="source", data=df, height=6, sharey=False, legend_out=False)
g.map(plt.scatter, "x", "y", alpha=0.7, s=100, lw=2, edgecolor="w")
g.axes[0][0].plot(dfp_lin["x"], dfp_lin["y"], "--", alpha=0.6, color="C0")
g.axes[0][1].plot(dfp_quad["x"], dfp_quad["y"], "--", alpha=0.6, color="C0")
def plot_annotated_trace(traces):
"""
Convenience function:
Plot traces with overlaid means and values
"""
summary = az.summary(traces, stat_funcs={"mean": np.mean}, extend=False)
ax = az.plot_trace(
traces,
lines=tuple([(k, {}, v["mean"]) for k, v in summary.iterrows()]),
)
for i, mn in enumerate(summary["mean"].values):
ax[i, 0].annotate(
f"{mn:.2f}",
xy=(mn, 0),
xycoords="data",
xytext=(5, 10),
textcoords="offset points",
rotation=90,
va="bottom",
fontsize="large",
color="C0",
)
def plot_posterior_cr(models, idatas, rawdata, xlims, datamodelnm="linear", modelnm="k1"):
"""
Convenience function:
Plot posterior predictions with credible regions shown as filled areas.
"""
# Get traces and calc posterior prediction for npoints in x
npoints = 100
mdl = models[modelnm]
trc = idatas[modelnm].posterior.copy().drop_vars("y_sigma")
da = xr.concat([var for var in trc.values()], dim="order")
ordr = int(modelnm[-1:])
x = xr.DataArray(np.linspace(xlims[0], xlims[1], npoints), dims=["x_plot"])
pwrs = xr.DataArray(np.arange(ordr + 1), dims=["order"])
X = x**pwrs
cr = xr.dot(X, da, dims="order")
# Calculate credible regions and plot over the datapoints
qs = cr.quantile([0.025, 0.25, 0.5, 0.75, 0.975], dim=("chain", "draw"))
f, ax1d = plt.subplots(1, 1, figsize=(7, 7))
f.suptitle(
f"Posterior Predictive Fit -- Data: {datamodelnm} -- Model: {modelnm}",
fontsize=16,
)
ax1d.fill_between(
x, qs.sel(quantile=0.025), qs.sel(quantile=0.975), alpha=0.5, color="C0", label="CR 95%"
)
ax1d.fill_between(
x, qs.sel(quantile=0.25), qs.sel(quantile=0.75), alpha=0.5, color="C3", label="CR 50%"
)
ax1d.plot(x, qs.sel(quantile=0.5), alpha=0.6, color="C4", label="Median")
ax1d.scatter(rawdata["x"], rawdata["y"], alpha=0.7, s=100, lw=2, edgecolor="w")
ax1d.legend()
ax1d.set_xlim(xlims)
生成玩具数据集#
交互式草拟数据#
在本笔记本的其余部分中，我们将使用分别由线性和二次模型创建的两个玩具数据集，以便我们可以更好地评估模型选择的效果。
现在，让我们使用交互式会话来探索本Notebook中的数据生成函数，并感受一下我们可以生成的数据的可能性。
\[y_{i} = a + bx_{i} + cx_{i}^{2} + \epsilon_{i}\]
其中：
\(i \in n\) 数据点
\[\epsilon \sim \mathcal{N}(0,latent\_sigma\_y)\]
关于异常值的说明
我们可以使用值
p来设置伯努利分布下“异常值”的（近似）比例。这些异常值的
latent_sigma_y大10倍这些异常值在返回的数据集中被标记，并且可能对其他建模有用，请参阅另一个示例笔记本：GLM：使用自定义似然进行异常值分类的稳健回归
interactive(
interact_dataset,
n=[5, 50, 5],
p=[0, 0.5, 0.05],
a=[-50, 50],
b=[-10, 10],
c=[-3, 3],
latent_sigma_y=[0, 1000, 50],
)
观察：
我已经展示了
latent_error在误差条中，但这只是出于兴趣，因为这显示了我们想象中创建数据的任何“物理过程”中的固有噪声。没有测量误差。
创建为异常值的数据点以红色显示，仅作为参考。
创建用于建模的数据集#
我们可以使用上述交互式图表来感受参数的效果。现在我们将创建两个固定的数据集，用于本笔记本的其余部分。
首先，我们将创建一个带有小噪声的线性模型。保持简单。
其次，一个带有小噪声的二次模型
n = 30
df_lin, dfp_lin = generate_data(n=n, p=0, a=-30, b=5, c=0, latent_sigma_y=40, seed=RANDOM_SEED)
df_quad, dfp_quad = generate_data(n=n, p=0, a=-200, b=2, c=3, latent_sigma_y=500, seed=RANDOM_SEED)
散点图与模型线
plot_datasets(df_lin, df_quad, dfp_lin, dfp_quad)
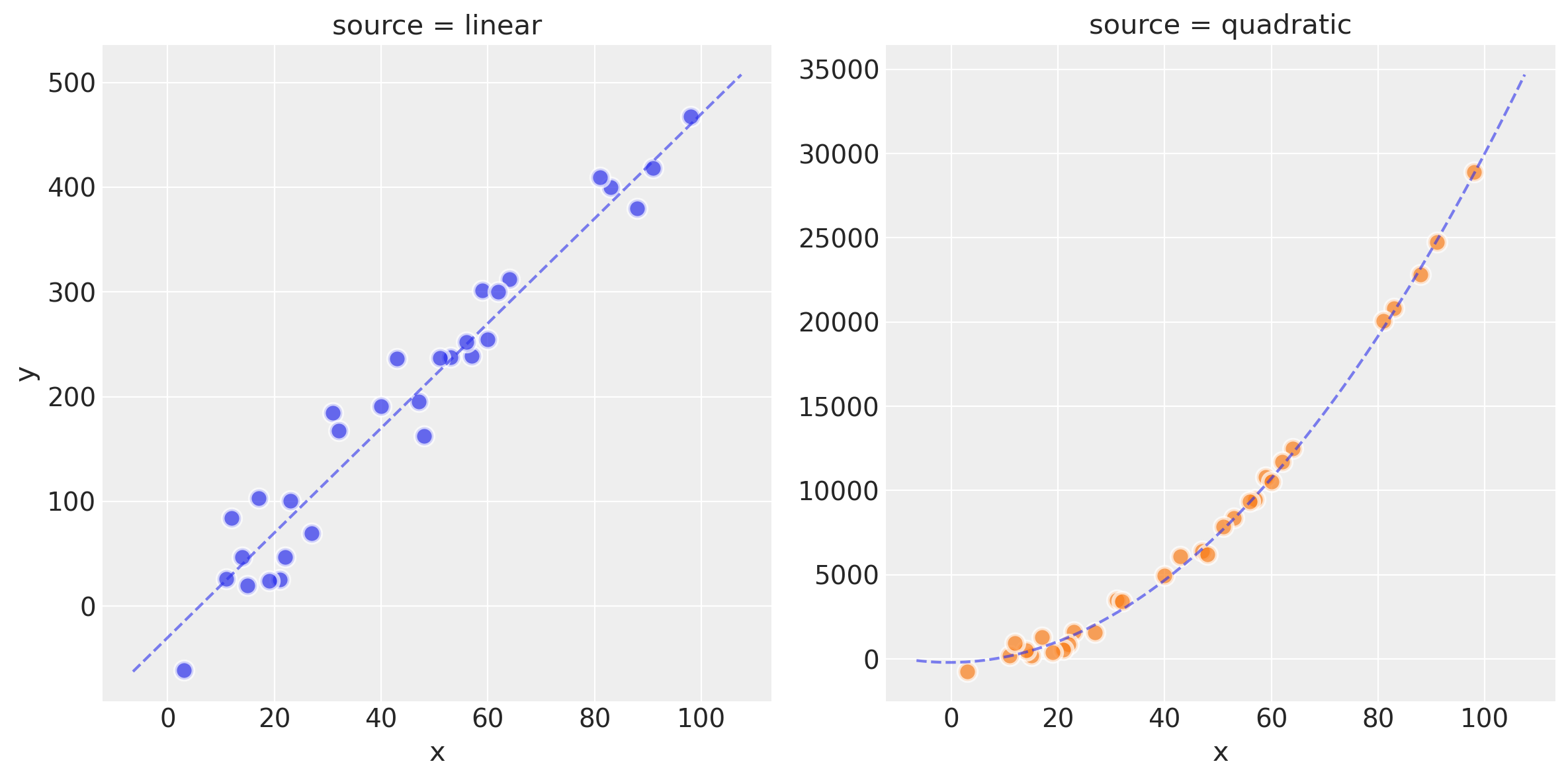
观察：
我们现在有两个数据集
df_lin和df_quad，分别由线性模型和二次模型创建。您可以在上面的散点图中看到原始数据、理想模型拟合以及潜在噪声的影响
在本笔记本的以下图中，线性生成的数据将以蓝色显示，而二次生成的数据将以绿色显示。
标准化#
dfs_lin = df_lin.copy()
dfs_lin["x"] = (df_lin["x"] - df_lin["x"].mean()) / df_lin["x"].std()
dfs_quad = df_quad.copy()
dfs_quad["x"] = (df_quad["x"] - df_quad["x"].mean()) / df_quad["x"].std()
创建用于后续 ylim xim 的范围
dfs_lin_xlims = (
dfs_lin["x"].min() - np.ptp(dfs_lin["x"].values) / 10,
dfs_lin["x"].max() + np.ptp(dfs_lin["x"].values) / 10,
)
dfs_lin_ylims = (
dfs_lin["y"].min() - np.ptp(dfs_lin["y"].values) / 10,
dfs_lin["y"].max() + np.ptp(dfs_lin["y"].values) / 10,
)
dfs_quad_ylims = (
dfs_quad["y"].min() - np.ptp(dfs_quad["y"].values) / 10,
dfs_quad["y"].max() + np.ptp(dfs_quad["y"].values) / 10,
)
演示简单线性模型#
这个线性模型非常简单且传统，是一个带有L2约束的OLS（岭回归）：
\[y = a + bx + \epsilon\]
使用显式 PyMC3 方法定义模型#
with pm.Model() as mdl_ols:
## define Normal priors to give Ridge regression
b0 = pm.Normal("Intercept", mu=0, sigma=100)
b1 = pm.Normal("x", mu=0, sigma=100)
## define Linear model
yest = b0 + b1 * df_lin["x"]
## define Normal likelihood with HalfCauchy noise (fat tails, equiv to HalfT 1DoF)
y_sigma = pm.HalfCauchy("y_sigma", beta=10)
likelihood = pm.Normal("likelihood", mu=yest, sigma=y_sigma, observed=df_lin["y"])
idata_ols = pm.sample(2000, return_inferencedata=True)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, x, Intercept]
100.00% [12000/12000 00:04<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 5 seconds.
The acceptance probability does not match the target. It is 0.886314395097965, but should be close to 0.8. Try to increase the number of tuning steps.
plt.rcParams["figure.constrained_layout.use"] = True
plot_annotated_trace(idata_ols)
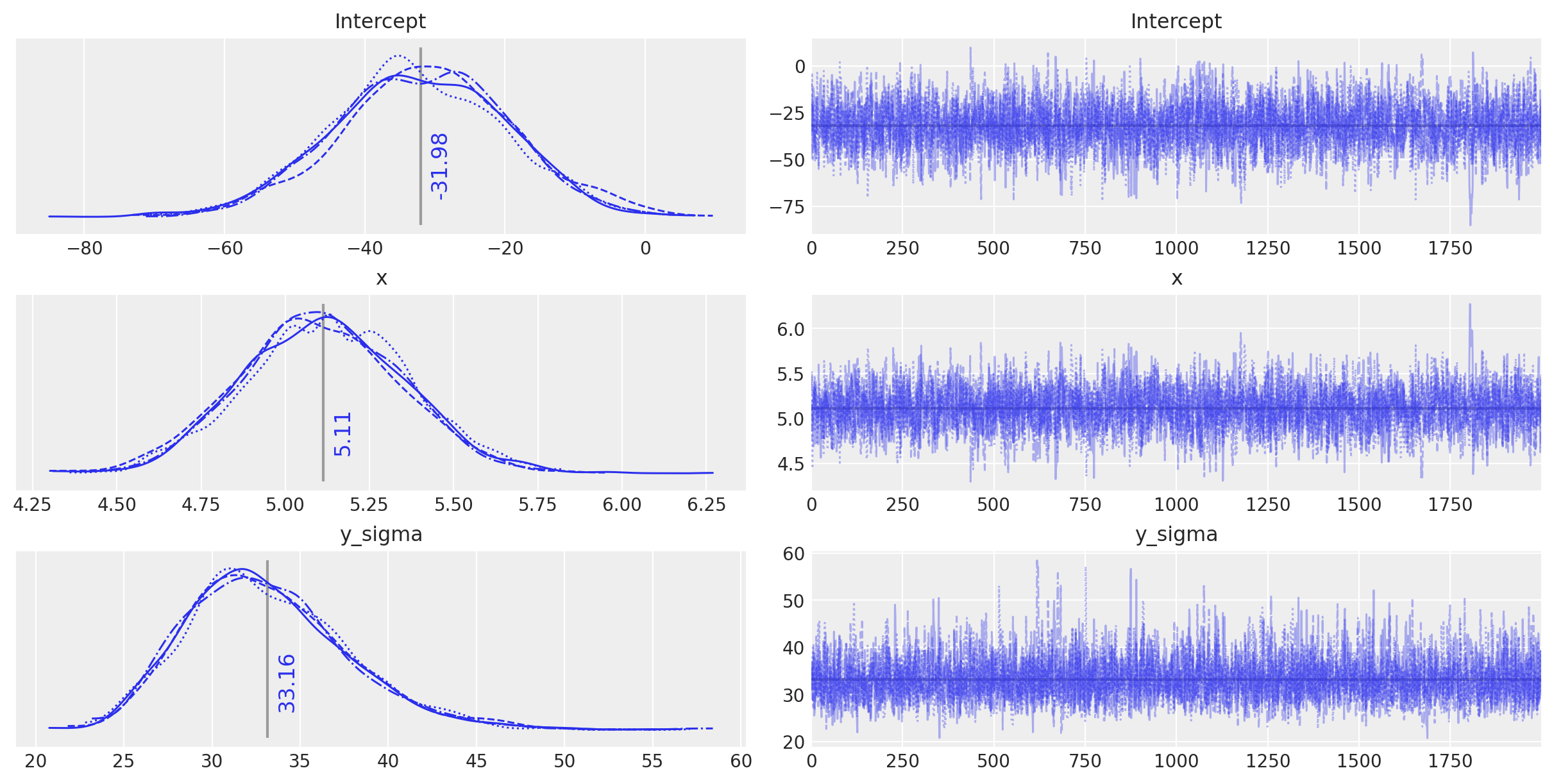
观察：
这个简单的OLS在模型参数上做出了相当不错的猜测——毕竟数据生成得相当简单——但它似乎确实被固有的噪声稍微迷惑了。
使用Bambi定义模型#
Bambi 可以使用 formulae 风格的公式语法来定义模型。这看起来非常有用，特别是用于在更少的代码行中定义简单的回归模型。
这里是与上面相同的OLS模型，使用bambi定义。
# Define priors for intercept and regression coefficients.
priors = {
"Intercept": bmb.Prior("Normal", mu=0, sigma=100),
"x": bmb.Prior("Normal", mu=0, sigma=100),
}
model = bmb.Model("y ~ 1 + x", df_lin, priors=priors, family="gaussian")
idata_ols_glm = model.fit(draws=2000, tune=2000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, x]
100.00% [16000/16000 00:04<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 2_000 tune and 2_000 draw iterations (8_000 + 8_000 draws total) took 4 seconds.
plot_annotated_trace(idata_ols_glm)
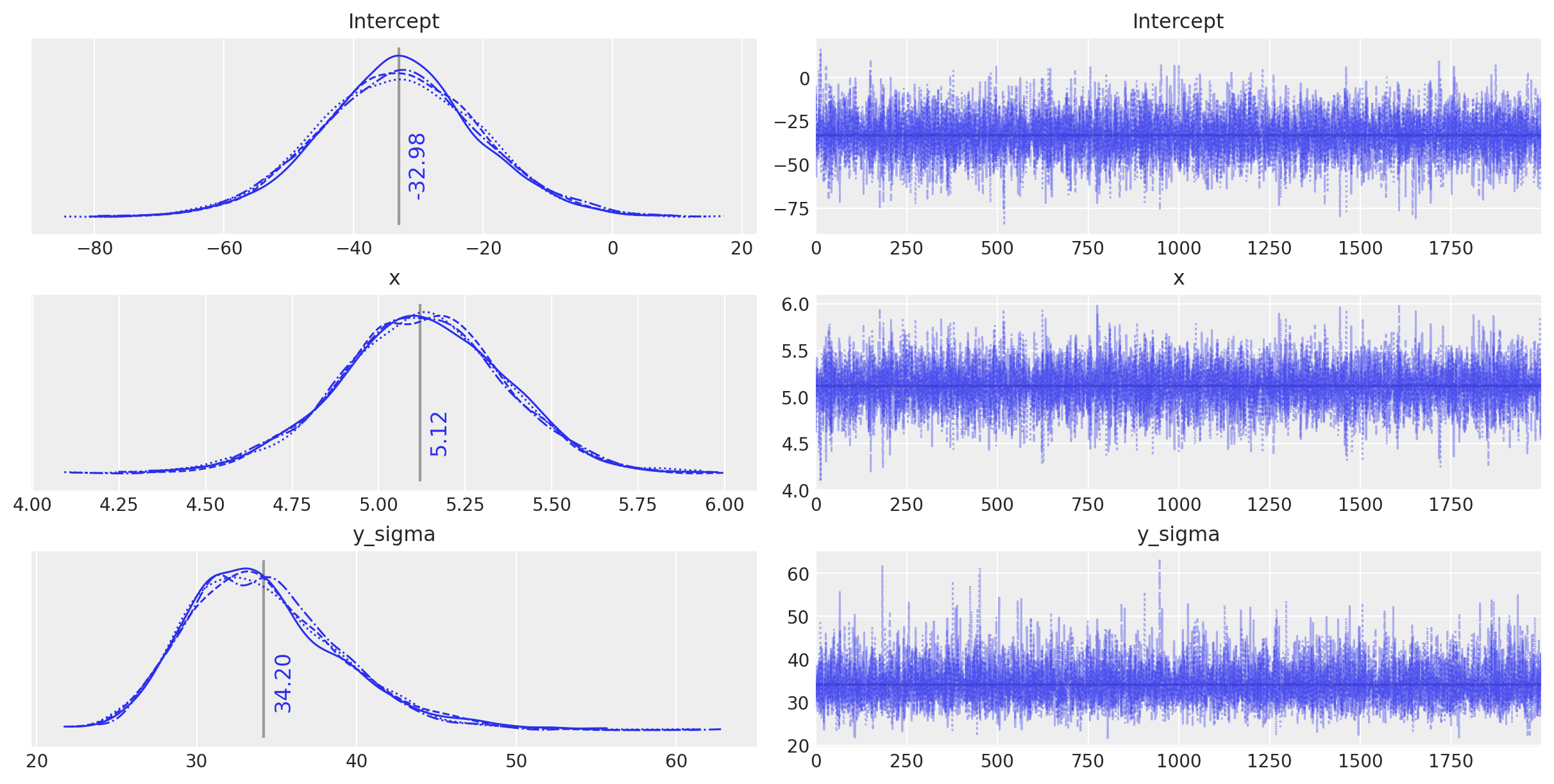
观察：
这个由
bambi定义的模型似乎表现得非常相似，并且找到了与常规定义的模型相同的参数值——任何差异都是由于采样的随机性造成的。我们可以很高兴地使用
bambi语法来构建下面的进一步模型，因为它使我们能够非常容易地创建一个小型模型工厂。
创建高阶线性模型#
回到这个笔记本的真正目的，即演示模型选择。
首先，让我们在每个玩具数据集上创建并运行一组多项式模型。默认情况下，这是针对1到5阶的模型。
创建和运行多项式模型#
我们正在创建5个多项式模型，并使用下面的函数create_poly_modelspec和run_models将每个模型拟合到选定的数据集上。
def create_poly_modelspec(k=1):
"""
Convenience function:
Create a polynomial modelspec string for bambi
"""
return ("y ~ 1 + x " + " ".join([f"+ np.power(x,{j})" for j in range(2, k + 1)])).strip()
def run_models(df, upper_order=5):
"""
Convenience function:
Fit a range of pymc3 models of increasing polynomial complexity.
Suggest limit to max order 5 since calculation time is exponential.
"""
models, results = dict(), dict()
for k in range(1, upper_order + 1):
nm = f"k{k}"
fml = create_poly_modelspec(k)
print(f"\nRunning: {nm}")
models[nm] = bmb.Model(
fml, df, priors={"intercept": bmb.Prior("Normal", mu=0, sigma=100)}, family="gaussian"
)
results[nm] = models[nm].fit(draws=2000, tune=1000, init="advi+adapt_diag")
return models, results
models_lin, idatas_lin = run_models(dfs_lin, 5)
Show code cell output
Running: k1
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
18.85% [9425/50000 00:00<00:03 Average Loss = 201.06]
Convergence achieved at 11400
Interrupted at 11,399 [22%]: Average Loss = 206
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, x]
100.00% [12000/12000 00:03<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 4 seconds.
Running: k2
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
18.26% [9129/50000 00:00<00:03 Average Loss = 205.62]
Convergence achieved at 11100
Interrupted at 11,099 [22%]: Average Loss = 210.55
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 2), x]
100.00% [12000/12000 00:03<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 4 seconds.
Running: k3
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
20.70% [10352/50000 00:01<00:04 Average Loss = 207.62]
Convergence achieved at 11500
Interrupted at 11,499 [22%]: Average Loss = 213.58
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 3), np.power(x, 2), x]
100.00% [12000/12000 00:07<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 8 seconds.
Running: k4
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
22.68% [11339/50000 00:01<00:04 Average Loss = 209.36]
Convergence achieved at 11400
Interrupted at 11,399 [22%]: Average Loss = 216.86
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 4), np.power(x, 3), np.power(x, 2), x]
100.00% [12000/12000 00:10<00:00 Sampling 4 chains, 4 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 11 seconds.
There were 4 divergences after tuning. Increase `target_accept` or reparameterize.
The acceptance probability does not match the target. It is 0.8819029722250732, but should be close to 0.8. Try to increase the number of tuning steps.
Running: k5
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
22.21% [11103/50000 00:01<00:04 Average Loss = 209.47]
Convergence achieved at 11400
Interrupted at 11,399 [22%]: Average Loss = 219.06
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 5), np.power(x, 4), np.power(x, 3), np.power(x, 2), x]
100.00% [12000/12000 00:23<00:00 Sampling 4 chains, 131 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 23 seconds.
There were 14 divergences after tuning. Increase `target_accept` or reparameterize.
There were 94 divergences after tuning. Increase `target_accept` or reparameterize.
There were 16 divergences after tuning. Increase `target_accept` or reparameterize.
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 10% for some parameters.
models_quad, idatas_quad = run_models(dfs_quad, 5)
Show code cell output
Running: k1
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
19.58% [9789/50000 00:00<00:03 Average Loss = 331.38]
Convergence achieved at 9900
Interrupted at 9,899 [19%]: Average Loss = 336.87
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, x]
100.00% [12000/12000 00:04<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 5 seconds.
Running: k2
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
18.23% [9115/50000 00:00<00:04 Average Loss = 340.37]
Convergence achieved at 9900
Interrupted at 9,899 [19%]: Average Loss = 346.3
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 2), x]
100.00% [12000/12000 00:05<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 6 seconds.
Running: k3
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
16.44% [8221/50000 00:00<00:04 Average Loss = 348.56]
Convergence achieved at 9900
Interrupted at 9,899 [19%]: Average Loss = 354.21
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 3), np.power(x, 2), x]
100.00% [12000/12000 00:07<00:00 Sampling 4 chains, 43 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 8 seconds.
There were 43 divergences after tuning. Increase `target_accept` or reparameterize.
The acceptance probability does not match the target. It is 0.6356752238454105, but should be close to 0.8. Try to increase the number of tuning steps.
The number of effective samples is smaller than 25% for some parameters.
Running: k4
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
19.62% [9812/50000 00:01<00:04 Average Loss = 354.73]
Convergence achieved at 9900
Interrupted at 9,899 [19%]: Average Loss = 361.87
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 4), np.power(x, 3), np.power(x, 2), x]
100.00% [12000/12000 00:15<00:00 Sampling 4 chains, 3 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 16 seconds.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
Running: k5
Auto-assigning NUTS sampler...
Initializing NUTS using advi+adapt_diag...
18.53% [9267/50000 00:01<00:05 Average Loss = 361.43]
Convergence achieved at 9900
Interrupted at 9,899 [19%]: Average Loss = 368.94
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [y_sigma, Intercept, np.power(x, 5), np.power(x, 4), np.power(x, 3), np.power(x, 2), x]
100.00% [12000/12000 00:30<00:00 Sampling 4 chains, 141 divergences]
Sampling 4 chains for 1_000 tune and 2_000 draw iterations (4_000 + 8_000 draws total) took 31 seconds.
There were 20 divergences after tuning. Increase `target_accept` or reparameterize.
The acceptance probability does not match the target. It is 0.9001195215217999, but should be close to 0.8. Try to increase the number of tuning steps.
There were 85 divergences after tuning. Increase `target_accept` or reparameterize.
There were 36 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
查看后验预测拟合#
对于线性生成的数据，让我们交互式地查看模型k1到k5的后验预测拟合。
如上图的似然图所示，高阶多项式模型在函数中表现出一些相当剧烈的波动，以（过度）拟合数据
interactive(
plot_posterior_cr,
models=fixed(models_lin),
idatas=fixed(idatas_lin),
rawdata=fixed(dfs_lin),
xlims=fixed(dfs_lin_xlims),
datamodelnm=fixed("linear"),
modelnm=["k1", "k2", "k3", "k4", "k5"],
)
使用WAIC比较模型#
广泛适用信息准则（WAIC）可以使用数值技术来计算模型的拟合优度。详情请参见。
观察：
我们得到三种不同的测量结果：
waic: 广泛适用的信息准则（或“Watanabe–Akaike信息准则”）
waic_se: waic的标准误差
p_waic: 有效参数数量
在这种情况下，我们关注的是WAIC得分。我们还绘制了估计得分的标准误差误差条。这让我们更准确地了解它们可能相差多少。
dfwaic_lin = az.compare(idatas_lin, ic="WAIC")
dfwaic_quad = az.compare(idatas_quad, ic="WAIC")
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:1491: UserWarning: For one or more samples the posterior variance of the log predictive densities exceeds 0.4. This could be indication of WAIC starting to fail.
See http://arxiv.org/abs/1507.04544 for details
warnings.warn(
dfwaic_lin
| rank | waic | p_waic | d_waic | weight | se | dse | warning | waic_scale | |
|---|---|---|---|---|---|---|---|---|---|
| k1 | 0 | -149.117557 | 2.345789 | 0.000000 | 1.000000e+00 | 2.712912 | 0.000000 | False | log |
| k2 | 1 | -149.602476 | 3.020848 | 0.484919 | 6.401130e-16 | 2.837751 | 0.803918 | True | log |
| k3 | 2 | -150.602409 | 3.721614 | 1.484851 | 2.407190e-15 | 2.777387 | 0.853239 | True | log |
| k4 | 3 | -151.411297 | 4.254917 | 2.293740 | 2.194139e-15 | 2.684069 | 0.878195 | True | log |
| k5 | 4 | -152.481775 | 5.040347 | 3.364217 | 0.000000e+00 | 2.662009 | 0.806270 | True | log |
dfwaic_quad
| rank | waic | p_waic | d_waic | weight | se | dse | warning | waic_scale | |
|---|---|---|---|---|---|---|---|---|---|
| k2 | 0 | -225.391799 | 3.002856 | 0.000000 | 1.000000e+00 | 2.818772 | 0.000000 | True | log |
| k3 | 1 | -226.368588 | 3.709239 | 0.976789 | 0.000000e+00 | 2.762794 | 0.327095 | True | log |
| k4 | 2 | -227.392991 | 4.444871 | 2.001191 | 0.000000e+00 | 2.720125 | 0.636527 | True | log |
| k5 | 3 | -228.251205 | 4.943613 | 2.859405 | 0.000000e+00 | 2.597084 | 0.776222 | True | log |
| k1 | 4 | -274.311114 | 3.433617 | 48.919315 | 2.383094e-11 | 3.916081 | 4.858806 | True | log |
_, axs = plt.subplots(1, 2)
ax = axs[0]
az.plot_compare(dfwaic_lin, ax=ax)
ax.set_title("Linear data")
ax = axs[1]
az.plot_compare(dfwaic_quad, ax=ax)
ax.set_title("Quadratic data");
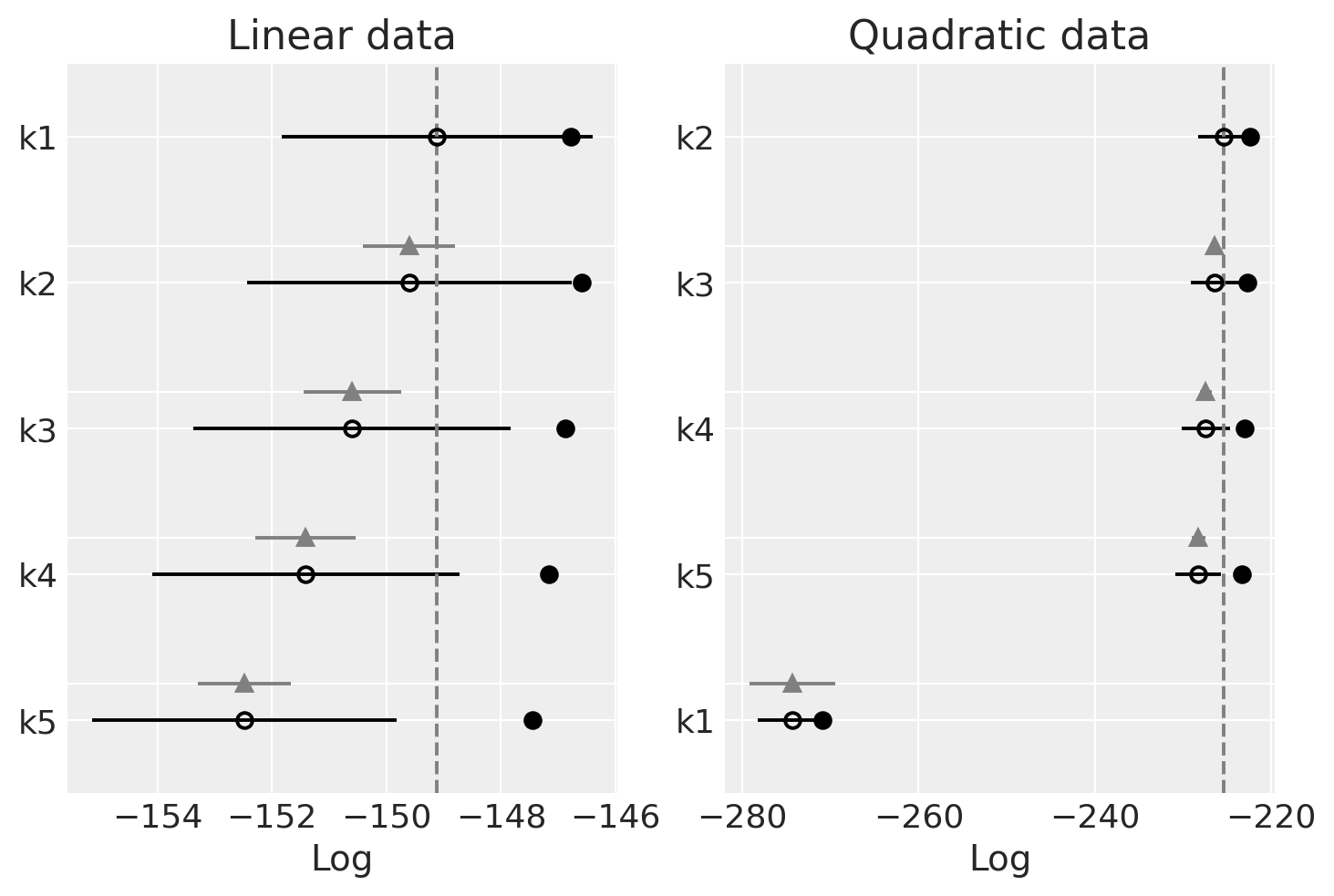
观察
我们应该选择具有更高WAIC的模型
线性生成的数据（左侧）：
WAIC 在不同模型中似乎相当平稳
WAIC 似乎最适合（最高）简单的模型。
二次生成的数据（右侧）：
WAIC在各模型中也非常平坦
最差的WAIC是针对k1的，它不够灵活，无法很好地拟合数据。
对于其余部分，WAIC 相当平坦，但最高的是 k2，正如预期的那样，随着阶数的增加，WAIC 会下降。阶数越高，模型的复杂度越高，但拟合优度基本相同。由于复杂度较高的模型会受到惩罚，我们可以看到我们如何选择能够拟合数据的最简单模型。
比较留一法交叉验证 [LOO]#
留一法交叉验证或K折交叉验证是另一种非常通用的模型选择方法。然而，要实现K折交叉验证，我们需要反复划分数据并在每个分区上拟合模型。这可能会非常耗时（计算时间大约增加K倍）。在这里，我们应用了数值方法，使用后验迹线，如中所建议的。
dfloo_lin = az.compare(idatas_lin, ic="LOO")
dfloo_quad = az.compare(idatas_quad, ic="LOO")
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:703: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:703: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:703: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
warnings.warn(
/home/oriol/miniconda3/envs/pymc-v3/lib/python3.9/site-packages/arviz/stats/stats.py:703: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
warnings.warn(
dfloo_lin
| rank | loo | p_loo | d_loo | weight | se | dse | warning | loo_scale | |
|---|---|---|---|---|---|---|---|---|---|
| k1 | 0 | -149.143334 | 2.371565 | 0.000000 | 1.000000e+00 | 2.719166 | 0.000000 | False | log |
| k2 | 1 | -149.692788 | 3.111160 | 0.549454 | 1.770806e-14 | 2.854122 | 0.808749 | False | log |
| k3 | 2 | -150.815225 | 3.934430 | 1.671890 | 1.261129e-14 | 2.809695 | 0.852309 | False | log |
| k4 | 3 | -151.875401 | 4.719021 | 2.732067 | 8.919651e-15 | 2.750613 | 0.967395 | True | log |
| k5 | 4 | -153.319706 | 5.878278 | 4.176372 | 0.000000e+00 | 2.805217 | 1.058934 | True | log |
dfloo_quad
| rank | loo | p_loo | d_loo | weight | se | dse | warning | loo_scale | |
|---|---|---|---|---|---|---|---|---|---|
| k2 | 0 | -225.464584 | 3.075641 | 0.000000 | 1.000000e+00 | 2.833440 | 0.000000 | False | log |
| k3 | 1 | -226.535084 | 3.875735 | 1.070500 | 1.290357e-12 | 2.784418 | 0.362643 | False | log |
| k4 | 2 | -227.987866 | 5.039746 | 2.523282 | 1.286804e-12 | 2.823319 | 0.882205 | True | log |
| k5 | 3 | -229.054152 | 5.746561 | 3.589568 | 1.116274e-12 | 2.740229 | 1.036157 | True | log |
| k1 | 4 | -274.409459 | 3.531961 | 48.944875 | 0.000000e+00 | 3.979691 | 4.908271 | False | log |
_, axs = plt.subplots(1, 2)
ax = axs[0]
az.plot_compare(dfloo_lin, ax=ax)
ax.set_title("Linear data")
ax = axs[1]
az.plot_compare(dfloo_quad, ax=ax)
ax.set_title("Quadratic data");
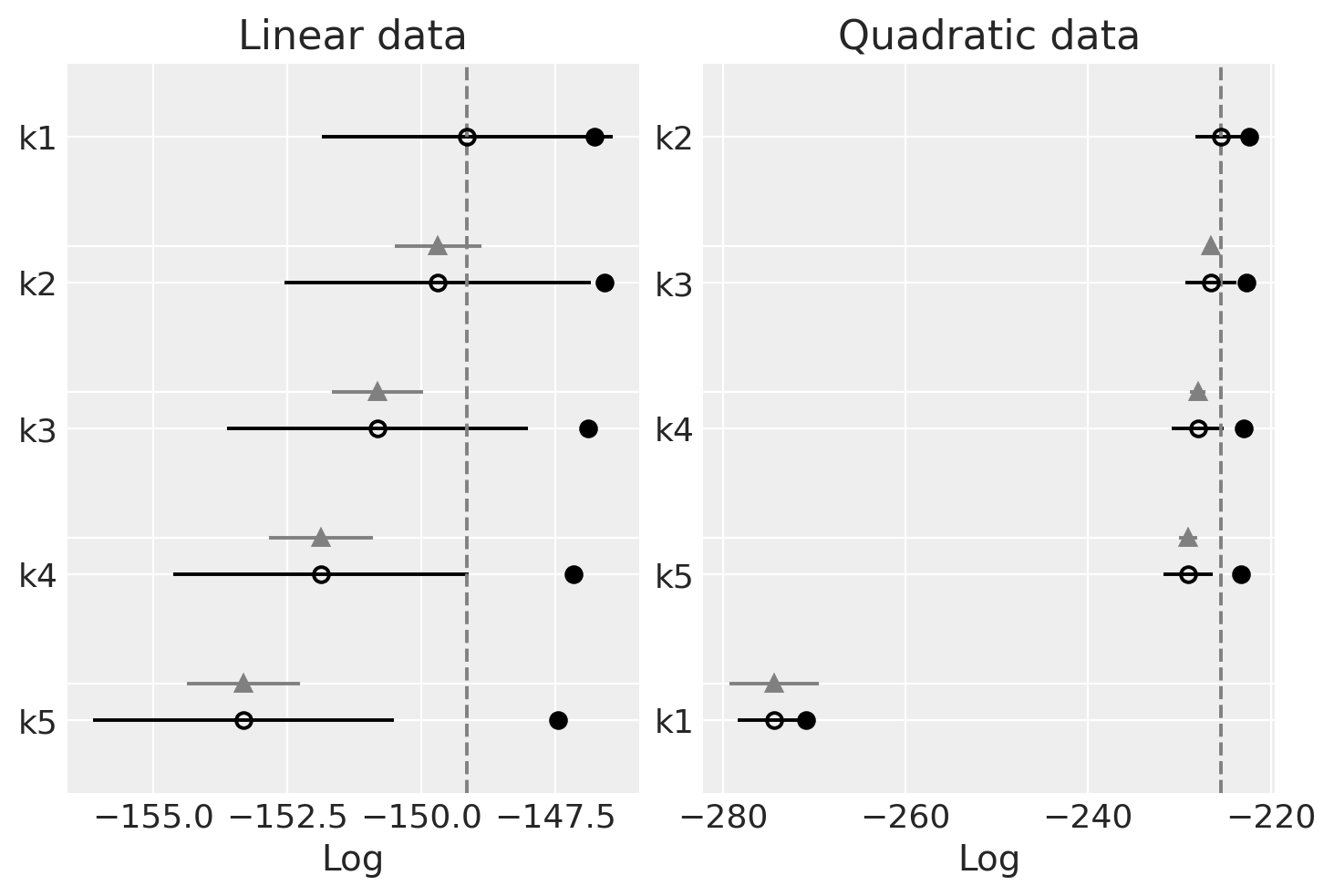
观察
我们应该选择具有更高LOO的模型。你可以看到LOO与WAIC几乎相同。这是因为WAIC在渐近情况下等于LOO。然而，在有限情况下（在弱先验或影响观察下），PSIS-LOO据说比WAIC更稳健。
线性生成的数据（左侧）：
LOO 在不同模型中也非常平坦
LOO 对于更简单的模型似乎也是最好的（最高的）。
二次生成的数据（右侧）：
与WAIC相同的模式
最后的评论和建议#
重要的是要记住，随着数据点的增加，真实的潜在模型（我们用来生成数据的模型）应该优于其他模型。
有一些共识认为PSIS-LOO提供了模型质量的最佳指示。引用自avehtari的评论：“我也建议使用PSIS-LOO而不是WAIC，因为它更可靠，并且具有更好的诊断功能，如中所讨论的，但如果你坚持要使用一个信息准则，那么就保留WAIC”。
另外，渡边表示“WAIC 是比帕累托平滑重要性采样交叉验证更好的泛化误差近似器。帕累托平滑交叉验证可能比 WAIC 更好地近似交叉验证，然而，它并不是泛化误差的近似器”。
参考资料#
[1]
安藤友弘。用于评估分层贝叶斯和经验贝叶斯模型的贝叶斯预测信息准则。Biometrika，94(2):443–458，2007年。doi:10.1093/biomet/asm017。
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p theano,xarray
Last updated: Sat Jan 08 2022
Python implementation: CPython
Python version : 3.9.7
IPython version : 7.29.0
theano: 1.1.2
xarray: 0.20.1
arviz : 0.11.4
pandas : 1.3.4
numpy : 1.21.4
matplotlib: 3.4.3
seaborn : 0.11.2
bambi : 0.6.3
xarray : 0.20.1
pymc3 : 3.11.4
Watermark: 2.2.0
许可证声明#
本示例库中的所有笔记本均在MIT许可证下提供，该许可证允许修改和重新分发，前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本，请使用Zenodo为pymc-examples仓库提供的DOI。
重要
许多笔记本是从其他来源改编的：博客、书籍……在这种情况下，您应该引用原始来源。
同时记得引用代码中使用的相关库。
这是一个BibTeX的引用模板：
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像：