GLM: 负二项回归

注意

本笔记本使用了不是 PyMC 依赖项的库，因此需要专门安装这些库才能运行此笔记本。打开下面的下拉菜单以获取更多指导。

Extra dependencies install instructions

为了在本地或binder上运行此笔记本，您不仅需要一个安装了所有可选依赖项的PyMC工作环境，还需要安装一些额外的依赖项。有关安装PyMC本身的建议，请参阅安装

您可以使用您喜欢的包管理器安装这些依赖项，我们提供了以下作为示例的pip和conda命令。

$ pip install seaborn

请注意，如果您想（或需要）从笔记本内部而不是命令行安装软件包，您可以通过运行pip命令的变体来安装软件包：

导入系统

!{sys.executable} -m pip install seaborn

您不应运行!pip install，因为它可能会在不同的环境中安装包，即使安装了也无法从Jupyter笔记本中使用。

另一个替代方案是使用conda：

$ conda install seaborn

在安装科学计算Python包时，我们推荐使用conda forge

import arviz as az
import numpy as np
import pandas as pd
import pymc as pm
import seaborn as sns

from scipy import stats

RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)

%config InlineBackend.figure_format = "retina"
az.style.use("arviz-darkgrid")

本笔记本紧密跟随Jonathan Sedar的GLM泊松回归示例（该示例又受到Ian Osvald的项目的启发），除了这里的数据是负二项分布而不是泊松分布。

负二项回归用于对计数数据进行建模，这些数据的方差大于均值。负二项分布可以被视为泊松分布，其速率参数是伽马分布的，因此速率参数可以调整以解释增加的方差。

生成数据

与泊松回归示例一样，我们假设打喷嚏的发生率在某个基线水平，并且饮酒、不服用抗组胺药或两者都做会增加其频率。

泊松数据

首先，让我们看一下泊松回归示例中的一些泊松分布数据。

# Mean Poisson values
theta_noalcohol_meds = 1  # no alcohol, took an antihist
theta_alcohol_meds = 3  # alcohol, took an antihist
theta_noalcohol_nomeds = 6  # no alcohol, no antihist
theta_alcohol_nomeds = 36  # alcohol, no antihist

# Create samples
q = 1000
df_pois = pd.DataFrame(
    {
        "nsneeze": np.concatenate(
            (
                rng.poisson(theta_noalcohol_meds, q),
                rng.poisson(theta_alcohol_meds, q),
                rng.poisson(theta_noalcohol_nomeds, q),
                rng.poisson(theta_alcohol_nomeds, q),
            )
        ),
        "alcohol": np.concatenate(
            (
                np.repeat(False, q),
                np.repeat(True, q),
                np.repeat(False, q),
                np.repeat(True, q),
            )
        ),
        "nomeds": np.concatenate(
            (
                np.repeat(False, q),
                np.repeat(False, q),
                np.repeat(True, q),
                np.repeat(True, q),
            )
        ),
    }
)

df_pois.groupby(["nomeds", "alcohol"])["nsneeze"].agg(["mean", "var"])

		mean	var
nomeds	alcohol
False	False	1.047	1.127919
	True	2.986	2.960765
True	False	5.981	6.218858
	True	35.929	36.064023

由于泊松分布的随机变量的均值和方差相等，样本均值和方差非常接近。

负二项分布数据

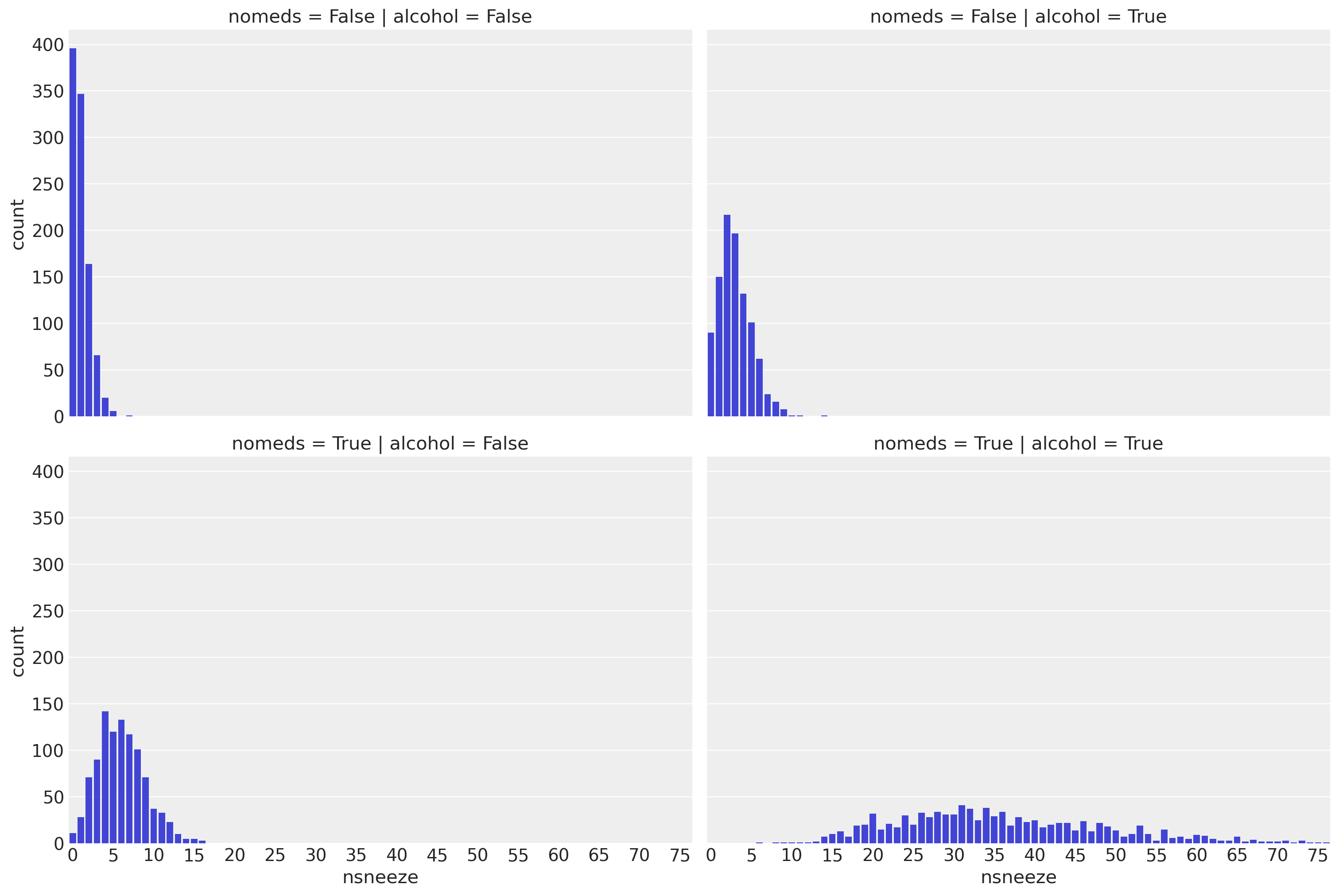
现在，假设数据集中的每个对象都患有流感，增加了他们打喷嚏的方差（并导致一些不幸的人每天打喷嚏超过70次）。如果打喷嚏的平均次数保持不变但方差增加，数据可能遵循负二项分布。

# Gamma shape parameter
alpha = 10


def get_nb_vals(mu, alpha, size):
    """Generate negative binomially distributed samples by
    drawing a sample from a gamma distribution with mean `mu` and
    shape parameter `alpha', then drawing from a Poisson
    distribution whose rate parameter is given by the sampled
    gamma variable.

    """

    g = stats.gamma.rvs(alpha, scale=mu / alpha, size=size)
    return stats.poisson.rvs(g)


# Create samples
n = 1000
df = pd.DataFrame(
    {
        "nsneeze": np.concatenate(
            (
                get_nb_vals(theta_noalcohol_meds, alpha, n),
                get_nb_vals(theta_alcohol_meds, alpha, n),
                get_nb_vals(theta_noalcohol_nomeds, alpha, n),
                get_nb_vals(theta_alcohol_nomeds, alpha, n),
            )
        ),
        "alcohol": np.concatenate(
            (
                np.repeat(False, n),
                np.repeat(True, n),
                np.repeat(False, n),
                np.repeat(True, n),
            )
        ),
        "nomeds": np.concatenate(
            (
                np.repeat(False, n),
                np.repeat(False, n),
                np.repeat(True, n),
                np.repeat(True, n),
            )
        ),
    }
)
df

	nsneeze	alcohol	nomeds
0	2	False	False
1	1	False	False
2	2	False	False
3	2	False	False
4	3	False	False
...	...	...	...
3995	28	True	True
3996	63	True	True
3997	19	True	True
3998	34	True	True
3999	40	True	True

4000行 × 3列

df.groupby(["nomeds", "alcohol"])["nsneeze"].agg(["mean", "var"])

		mean	var
nomeds	alcohol
False	False	0.990	1.137037
	True	2.983	4.030742
True	False	6.004	8.658643
	True	35.918	169.018294

与泊松回归示例一样，我们看到饮酒和/或不服用抗组胺药会增加打喷嚏率，程度各不相同。与该示例不同的是，对于每种alcohol和nomeds的组合，nsneeze的方差都大于均值。这表明泊松分布不适合这些数据，因为泊松分布的均值和方差是相等的。

可视化数据

g = sns.catplot(x="nsneeze", row="nomeds", col="alcohol", data=df, kind="count", aspect=1.5)

# Make x-axis ticklabels less crowded
ax = g.axes[1, 0]
labels = range(len(ax.get_xticklabels(which="both")))
ax.set_xticks(labels[::5])
ax.set_xticklabels(labels[::5]);

/opt/homebrew/Caskroom/miniconda/base/envs/pymc-dev/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
  self._figure.tight_layout(*args, **kwargs)
/opt/homebrew/Caskroom/miniconda/base/envs/pymc-dev/lib/python3.11/site-packages/seaborn/axisgrid.py:123: UserWarning: The figure layout has changed to tight
  self._figure.tight_layout(*args, **kwargs)

负二项回归

创建GLM模型

COORDS = {"regressor": ["nomeds", "alcohol", "nomeds:alcohol"], "obs_idx": df.index}

with pm.Model(coords=COORDS) as m_sneeze_inter:
    a = pm.Normal("intercept", mu=0, sigma=5)
    b = pm.Normal("slopes", mu=0, sigma=1, dims="regressor")
    alpha = pm.Exponential("alpha", 0.5)

    M = pm.ConstantData("nomeds", df.nomeds.to_numpy(), dims="obs_idx")
    A = pm.ConstantData("alcohol", df.alcohol.to_numpy(), dims="obs_idx")
    S = pm.ConstantData("nsneeze", df.nsneeze.to_numpy(), dims="obs_idx")

    λ = pm.math.exp(a + b[0] * M + b[1] * A + b[2] * M * A)

    y = pm.NegativeBinomial("y", mu=λ, alpha=alpha, observed=S, dims="obs_idx")

    idata = pm.sample()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [intercept, slopes, alpha]

100.00% [8000/8000 00:10<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 11 seconds.

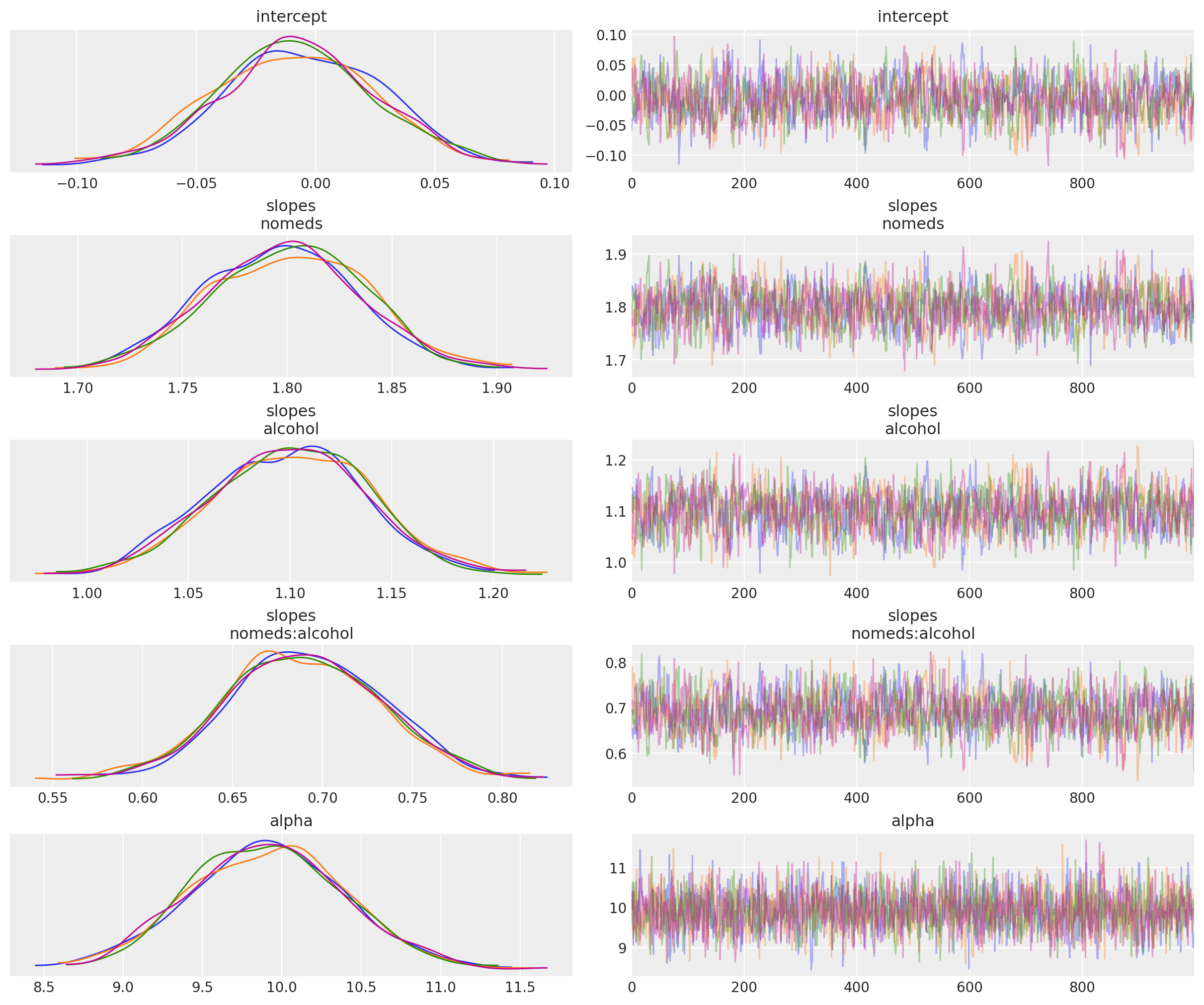
查看结果

az.plot_trace(idata, compact=False);

# Transform coefficients to recover parameter values
az.summary(np.exp(idata.posterior), kind="stats", var_names=["intercept", "slopes"])

	mean	sd	hdi_3%	hdi_97%
intercept	0.993	0.033	0.935	1.056
slopes[nomeds]	6.048	0.221	5.635	6.438
slopes[alcohol]	3.006	0.115	2.789	3.215
slopes[nomeds:alcohol]	1.995	0.086	1.842	2.163

az.summary(idata.posterior, kind="stats", var_names="alpha")

	mean	sd	hdi_3%	hdi_97%
alpha	9.909	0.487	9.05	10.887

均值接近我们在生成数据时指定的值：

• 基础利率是一个常数 1。

• 饮酒使基础率增加了两倍。

• 不服用抗组胺药会使基础率增加6倍。

• 饮酒且不服用抗组胺药会使预期发生率翻倍。如果它们是独立的，那么同时进行这两项会使基础发生率增加3*6=18倍，但实际上基础发生率增加了3*6*2=36倍。

最后，nsneeze_alpha 的平均值也非常接近其真实值 10。

另请参阅，bambi的负二项式示例以供进一步参考。

作者

• 由 Ian Ozsvald 创建

• 更新于 Abhipsha Das 在2021年8月

• 由 Benjamin Vincent 于2022年6月更新至PyMC v4

• 由 Wesley Boelrijk 于2023年9月更新至PyMC v5

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Mon Oct 16 2023

Python implementation: CPython
Python version       : 3.11.5
IPython version      : 8.15.0

pytensor: 2.16.1
xarray  : 2023.8.0

pymc   : 5.8.1
pandas : 2.1.0
seaborn: 0.13.0
numpy  : 1.25.2
arviz  : 0.16.1
scipy  : 1.11.2

Watermark: 2.4.3

许可证声明

本示例库中的所有笔记本均在MIT许可证下提供，该许可证允许修改和重新分发，前提是保留版权和许可证声明。

引用 PyMC 示例

要引用此笔记本，请使用Zenodo为pymc-examples仓库提供的DOI。

重要

许多笔记本是从其他来源改编的：博客、书籍……在这种情况下，您应该引用原始来源。

同时记得引用代码中使用的相关库。

这是一个BibTeX的引用模板：

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像：