LKJ Cholesky 协方差先验用于多元正态模型#

虽然逆Wishart分布是多元正态分布协方差矩阵的共轭先验，但它并不非常适合现代贝叶斯计算方法。因此，在为多元正态分布的协方差矩阵建模时，建议使用LKJ先验。

为了说明使用LKJ分布建模协方差，我们首先生成一个二维正态分布的样本数据集。

import arviz as az
import numpy as np
import pymc as pm

from matplotlib import pyplot as plt
from matplotlib.lines import Line2D
from matplotlib.patches import Ellipse

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v5.9.0

%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")

N = 10000

mu_actual = np.array([1.0, -2.0])
sigmas_actual = np.array([0.7, 1.5])
Rho_actual = np.matrix([[1.0, -0.4], [-0.4, 1.0]])

Sigma_actual = np.diag(sigmas_actual) * Rho_actual * np.diag(sigmas_actual)

x = rng.multivariate_normal(mu_actual, Sigma_actual, size=N)
Sigma_actual

matrix([[ 0.49, -0.42],
        [-0.42,  2.25]])

var, U = np.linalg.eig(Sigma_actual)
angle = 180.0 / np.pi * np.arccos(np.abs(U[0, 0]))

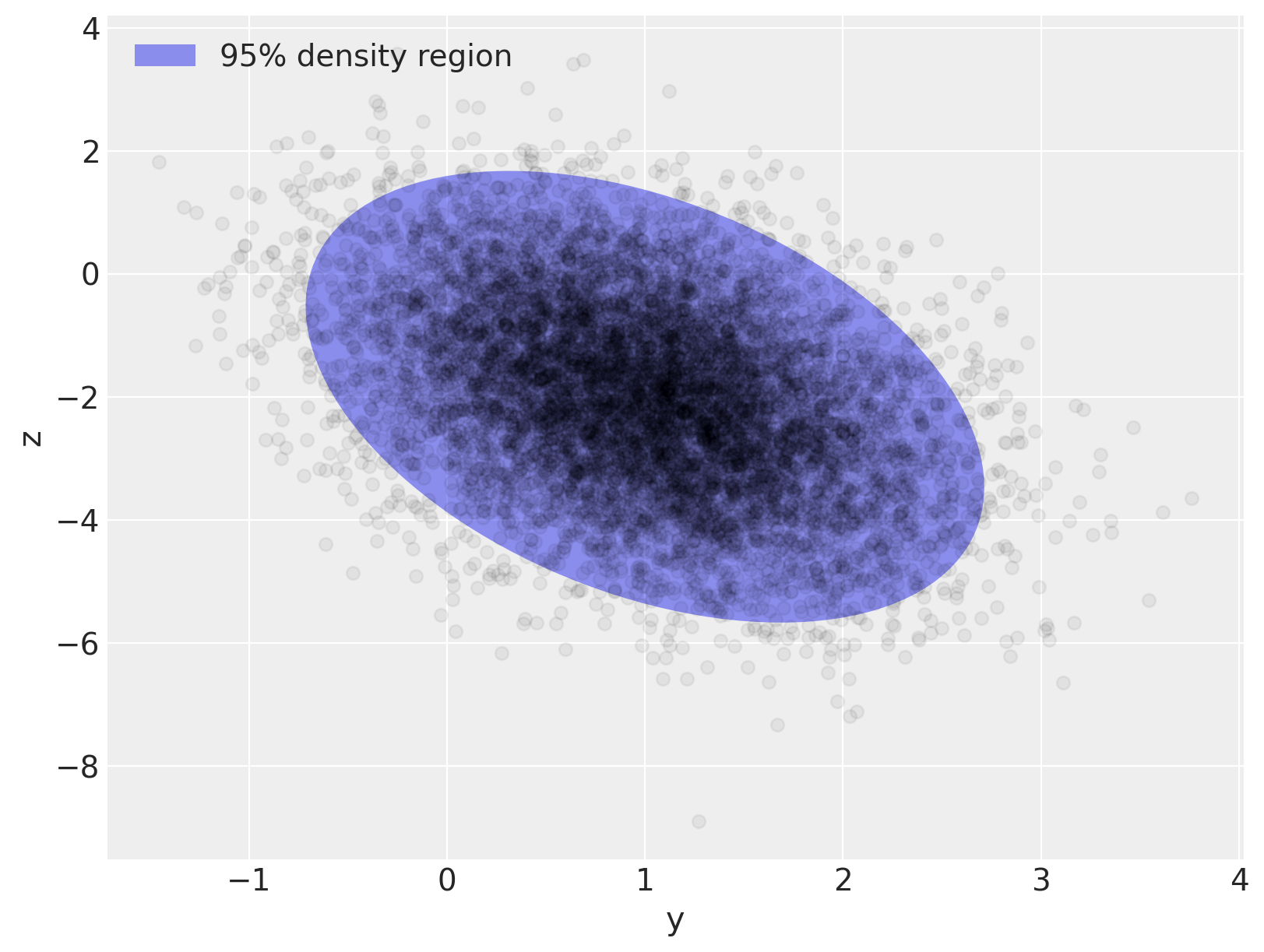
fig, ax = plt.subplots(figsize=(8, 6))

e = Ellipse(mu_actual, 2 * np.sqrt(5.991 * var[0]), 2 * np.sqrt(5.991 * var[1]), angle=angle)
e.set_alpha(0.5)
e.set_facecolor("C0")
e.set_zorder(10)
ax.add_artist(e)

ax.scatter(x[:, 0], x[:, 1], c="k", alpha=0.05, zorder=11)
ax.set_xlabel("y")
ax.set_ylabel("z")

rect = plt.Rectangle((0, 0), 1, 1, fc="C0", alpha=0.5)
ax.legend([rect], ["95% density region"], loc=2);
../_images/f859e4ca959a1c0fc8f886a6752ef8317cff5016e94dc17a7c1cc6ac2cd9535f.png

多元正态模型的抽样分布为 \(\mathbf{x} \sim N(\mu, \Sigma)\)，其中 \(\Sigma\) 是抽样分布的协方差矩阵，且 \(\Sigma_{ij} = \textrm{Cov}(x_i, x_j)\)。该分布的密度为

\[f(\mathbf{x}\ |\ \mu, \Sigma^{-1}) = (2 \pi)^{-\frac{k}{2}} |\Sigma|^{-\frac{1}{2}} \exp\left(-\frac{1}{2} (\mathbf{x} - \mu)^{\top} \Sigma^{-1} (\mathbf{x} - \mu)\right).\]

LKJ 分布提供了一个关于相关矩阵的先验，\(\mathbf{C} = \textrm{Corr}(x_i, x_j)\)，它与每个分量的标准差的先验结合，诱导出一个关于协方差矩阵的先验，\(\Sigma\)。由于反转 \(\Sigma\) 在数值上不稳定且效率低下，因此使用 \(\Sigma\) 的 Cholesky 分解，\(\Sigma = \mathbf{L} \mathbf{L}^{\top}\)，其中 \(\mathbf{L}\) 是一个下三角矩阵，在计算上是有优势的。这种分解允许使用回代法计算项 \((\mathbf{x} - \mu)^{\top} \Sigma^{-1} (\mathbf{x} - \mu)\)，这比直接矩阵求逆在数值上更稳定且更高效。

PyMC 支持通过 pymc.LKJCholeskyCov 分布对协方差矩阵的 Cholesky 分解使用 LKJ 先验。该分布具有参数 n 和 sd_dist，分别表示观测值的维度 \(\mathbf{x}\) 和分量标准差的 PyMC 分布。它还具有一个超参数 eta，用于控制 \(\mathbf{x}\) 分量之间的相关性程度。LKJ 分布具有密度 \(f(\mathbf{C}\ |\ \eta) \propto |\mathbf{C}|^{\eta - 1}\)，因此 \(\eta = 1\) 会导致相关矩阵上的均匀分布，而随着 \(\eta \to \infty\)，分量之间的相关性幅度会减小。

在这个例子中，我们使用 \(\textrm{Exponential}(1.0)\) 先验来建模标准差，并将相关矩阵建模为 \(\mathbf{C} \sim \textrm{LKJ}(\eta = 2)\)。

with pm.Model() as m:
    packed_L = pm.LKJCholeskyCov(
        "packed_L", n=2, eta=2.0, sd_dist=pm.Exponential.dist(1.0, shape=2), compute_corr=False
    )

由于\(\Sigma\)的Cholesky分解是下三角的，LKJCholeskyCov仅存储对角线和次对角线项，以提高效率：

packed_L.eval()

array([ 2.60423567, -1.28344686,  0.65139719])

我们使用 expand_packed_triangular 将这个向量转换为下三角矩阵 \(\mathbf{L}\)，它出现在 Cholesky 分解 \(\Sigma = \mathbf{L} \mathbf{L}^{\top}\) 中。

with m:
    L = pm.expand_packed_triangular(2, packed_L)
    Sigma = L.dot(L.T)

L.eval().shape

(2, 2)

然而，通常情况下，您会对相关矩阵和标准差的后验分布感兴趣，而不是对后验的Cholesky协方差矩阵本身感兴趣。为什么？因为相关性和标准差更容易解释，并且在模型中通常具有科学意义。从PyMC v4开始，compute_corr参数默认设置为True，这将返回一个由Cholesky分解、相关矩阵和标准差组成的元组。

coords = {"axis": ["y", "z"], "axis_bis": ["y", "z"], "obs_id": np.arange(N)}
with pm.Model(coords=coords) as model:
    chol, corr, stds = pm.LKJCholeskyCov(
        "chol", n=2, eta=2.0, sd_dist=pm.Exponential.dist(1.0, shape=2)
    )
    cov = pm.Deterministic("cov", chol.dot(chol.T), dims=("axis", "axis_bis"))

为了完成我们的模型，我们在\(\mu\)上放置了独立、弱正则化的先验，\(N(0, 1.5),\)：

with model:
    mu = pm.Normal("mu", 0.0, sigma=1.5, dims="axis")
    obs = pm.MvNormal("obs", mu, chol=chol, observed=x, dims=("obs_id", "axis"))

我们使用NUTS从这个模型中采样，并将轨迹传递给arviz进行汇总：

with model:
    trace = pm.sample(
        random_seed=rng,
        idata_kwargs={"dims": {"chol_stds": ["axis"], "chol_corr": ["axis", "axis_bis"]}},
    )
az.summary(trace, var_names="~chol", round_to=2)

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [chol, mu]
100.00% [8000/8000 00:31<00:00 Sampling 4 chains, 0 divergences] 
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 31 seconds.
/home/erik/mambaforge/envs/pymc_examples/lib/python3.11/site-packages/arviz/stats/diagnostics.py:592: RuntimeWarning: invalid value encountered in scalar divide
  (between_chain_variance / within_chain_variance + num_samples - 1) / (num_samples)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
mu[y] 1.00 0.01 0.99 1.01 0.0 0.0 4121.45 3183.18 1.0
mu[z] -2.01 0.01 -2.04 -1.99 0.0 0.0 4649.42 3413.88 1.0
chol_corr[y, y] 1.00 0.00 1.00 1.00 0.0 0.0 4000.00 4000.00 NaN
chol_corr[y, z] -0.40 0.01 -0.42 -0.39 0.0 0.0 4986.71 3442.98 1.0
chol_corr[z, y] -0.40 0.01 -0.42 -0.39 0.0 0.0 4986.71 3442.98 1.0
chol_corr[z, z] 1.00 0.00 1.00 1.00 0.0 0.0 3458.80 3722.51 1.0
chol_stds[y] 0.70 0.01 0.69 0.71 0.0 0.0 5112.65 3038.55 1.0
chol_stds[z] 1.49 0.01 1.47 1.51 0.0 0.0 5330.27 3156.89 1.0
cov[y, y] 0.49 0.01 0.48 0.51 0.0 0.0 5112.65 3038.55 1.0
cov[y, z] -0.42 0.01 -0.44 -0.40 0.0 0.0 4320.77 3391.79 1.0
cov[z, y] -0.42 0.01 -0.44 -0.40 0.0 0.0 4320.77 3391.79 1.0
cov[z, z] 2.23 0.03 2.17 2.28 0.0 0.0 5330.27 3156.89 1.0

采样进行得很顺利：没有分歧，且r-hat值良好（除了相关矩阵的对角元素 - 不过，这些并不令人担忧，因为对于每个链的每个样本，它们应该等于1，而常数值的方差是未定义的。如果对角元素之一有r_hat定义，这很可能是由于极小的数值误差）。

你也可以看到采样器恢复了真实的均值、相关性和标准差。通常，这在图表中会更加清晰：

az.plot_trace(
    trace,
    var_names="chol_corr",
    coords={"axis": "y", "axis_bis": "z"},
    lines=[("chol_corr", {}, Rho_actual[0, 1])],
);
../_images/353f15d322acedbcb9e93ff1c218a2165256fe0ee8b27022e32478c569437721.png 
az.plot_trace(
    trace,
    var_names=["~chol", "~chol_corr"],
    compact=True,
    lines=[
        ("mu", {}, mu_actual),
        ("cov", {}, Sigma_actual),
        ("chol_stds", {}, sigmas_actual),
    ],
);
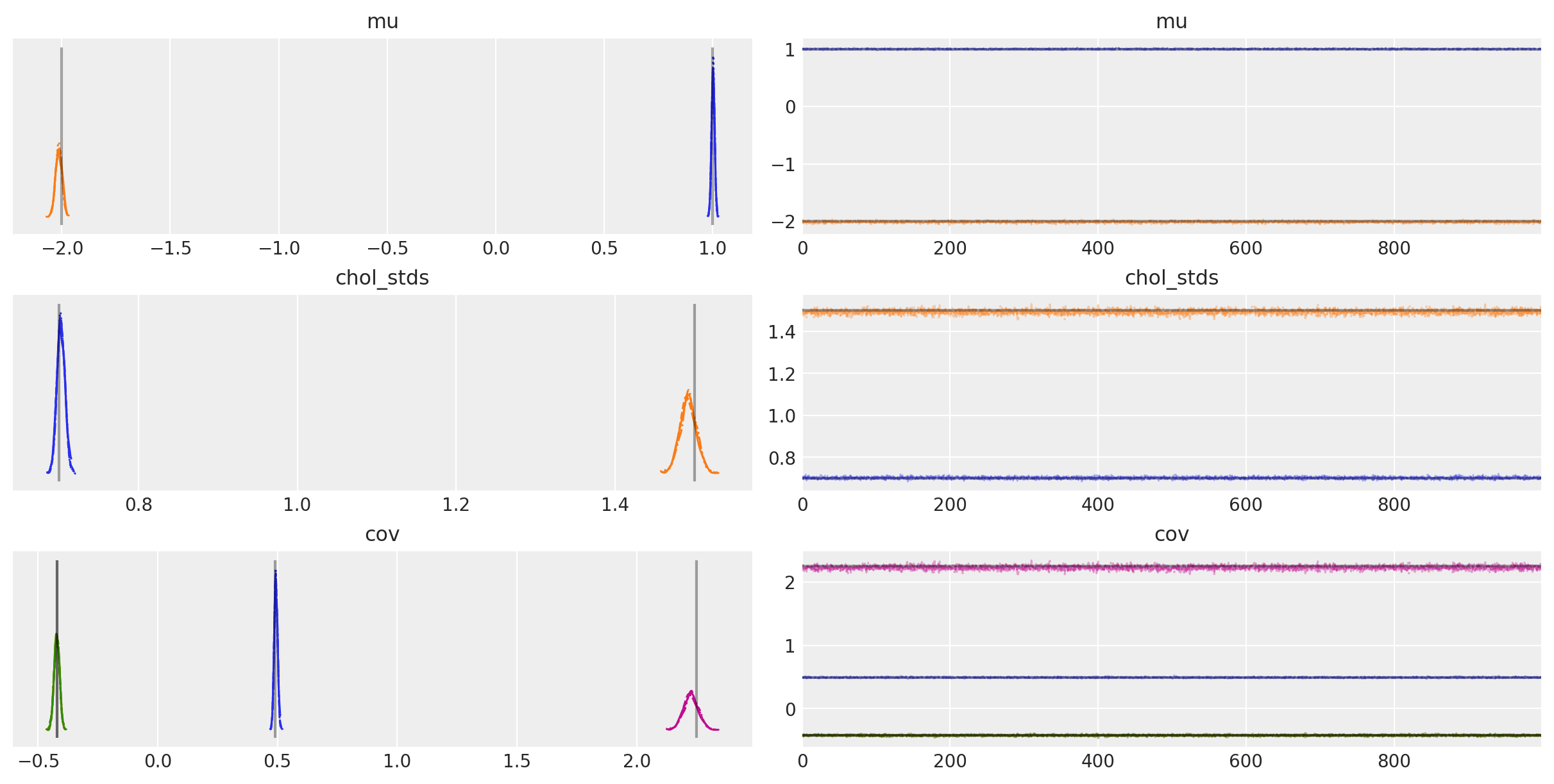
../_images/31c7852632e428c502f6472cfc8172db72ac3beff63aa0b17372d4a2b215401f.png

后验期望值非常接近每个分量的真实值！具体有多接近？让我们计算\(\mu\)和\(\Sigma\)的接近百分比：

mu_post = trace.posterior["mu"].mean(("chain", "draw")).values
(1 - mu_post / mu_actual).round(2)

array([-0.  , -0.01])

Sigma_post = trace.posterior["cov"].mean(("chain", "draw")).values
(1 - Sigma_post / Sigma_actual).round(2)

array([[-0.01, -0.  ],
       [-0.  ,  0.01]])

因此，后验均值在\(\mu\)和\(\Sigma\)的真实值的1%以内。

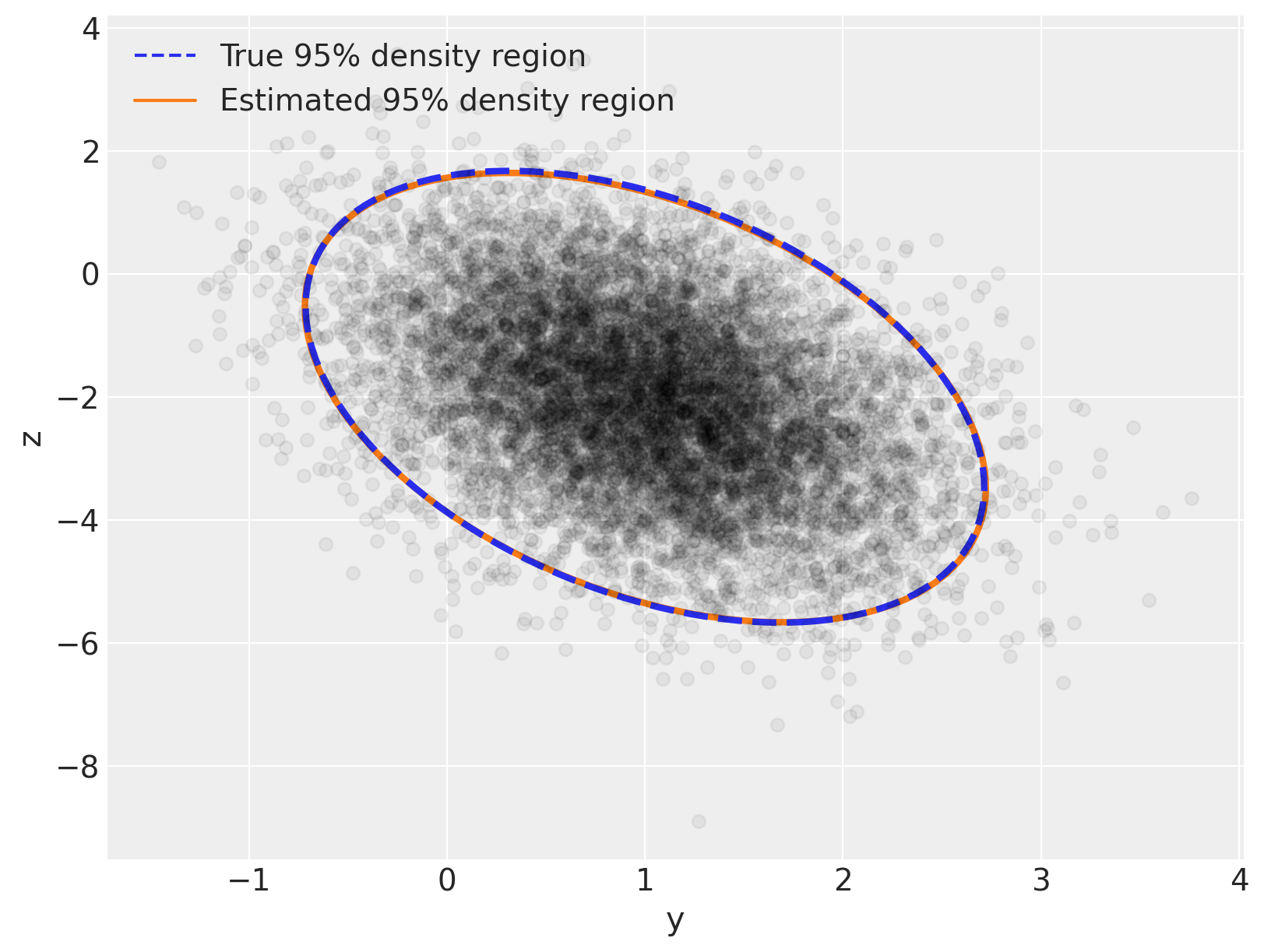
现在让我们复制我们在开始时绘制的图表，但让我们在真实分布的顶部叠加后验分布——你会看到两者之间有非常好的视觉一致性：

var_post, U_post = np.linalg.eig(Sigma_post)
angle_post = 180.0 / np.pi * np.arccos(np.abs(U_post[0, 0]))

fig, ax = plt.subplots(figsize=(8, 6))

e = Ellipse(
    mu_actual,
    2 * np.sqrt(5.991 * var[0]),
    2 * np.sqrt(5.991 * var[1]),
    angle=angle,
    linewidth=3,
    linestyle="dashed",
)
e.set_edgecolor("C0")
e.set_zorder(11)
e.set_fill(False)
ax.add_artist(e)

e_post = Ellipse(
    mu_post,
    2 * np.sqrt(5.991 * var_post[0]),
    2 * np.sqrt(5.991 * var_post[1]),
    angle=angle_post,
    linewidth=3,
)
e_post.set_edgecolor("C1")
e_post.set_zorder(10)
e_post.set_fill(False)
ax.add_artist(e_post)

ax.scatter(x[:, 0], x[:, 1], c="k", alpha=0.05, zorder=11)
ax.set_xlabel("y")
ax.set_ylabel("z")

line = Line2D([], [], color="C0", linestyle="dashed", label="True 95% density region")
line_post = Line2D([], [], color="C1", label="Estimated 95% density region")
ax.legend(
    handles=[line, line_post],
    loc=2,
);
../_images/0f00b23290a12d0321899f684b6108ccac834c6a555112ed39cf7beb7ba88ffa.png 
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Thu Oct 12 2023

Python implementation: CPython
Python version       : 3.11.6
IPython version      : 8.16.1

pytensor: 2.17.1
xarray  : 2023.9.0

numpy     : 1.25.2
matplotlib: 3.8.0
pymc      : 5.9.0
arviz     : 0.16.1

Watermark: 2.4.3