贝叶斯Copula估计：描述相关联合分布

问题

当我们处理多个变量（例如 \(a\) 和 \(b\)）时，我们通常希望以参数化的方式描述联合分布 \(P(a, b)\)。如果我们幸运的话，这个联合分布可能在某种方式上是“简单”的。例如，可能 \(a\) 和 \(b\) 在统计上是独立的，在这种情况下，我们可以将联合分布分解为 \(P(a, b) = P(a) P(b)\)，因此我们只需要找到 \(P(a)\) 和 \(P(b)\) 的适当参数化描述。即使这不适用，也可能 \(P(a, b)\) 可以通过简单的多元分布很好地描述，例如多元正态分布。

然而，当我们处理真实数据集时，通常会遇到复杂的关联结构，即\(P(a, b)\)，这意味着我们无法使用上述两种方法。因此，需要采用其他方法。

Copulas 来救援

这就是copulas发挥作用的地方。它们允许你通过一个简单的多元分布（如多元高斯分布）、两个边缘分布和一些变换来描述具有相关结构的复杂分布 \(P(a, b)\)。对于copulas的非常易懂的介绍，我们推荐阅读Thomas Wiecki的这篇博客文章。

本笔记本介绍了我们如何使用贝叶斯方法来描述具有相关结构的分布 \(P(a, b)\)，以推断copula的参数。我们将采用的总体方法如下图所示。

• 在底部，我们有我们的观测空间，数据存放在这里。

• 我们可以假设这些数据是通过从上到下的过程生成的——我们在多元正态空间中有一个多元正态分布，该分布经过两个阶段的转换，最终得到我们在观测空间中的数据。

• 我们可以访问观测空间中的数据，但我们可以通过从一个空间转换到另一个空间来推断多元正态空间中的参数。

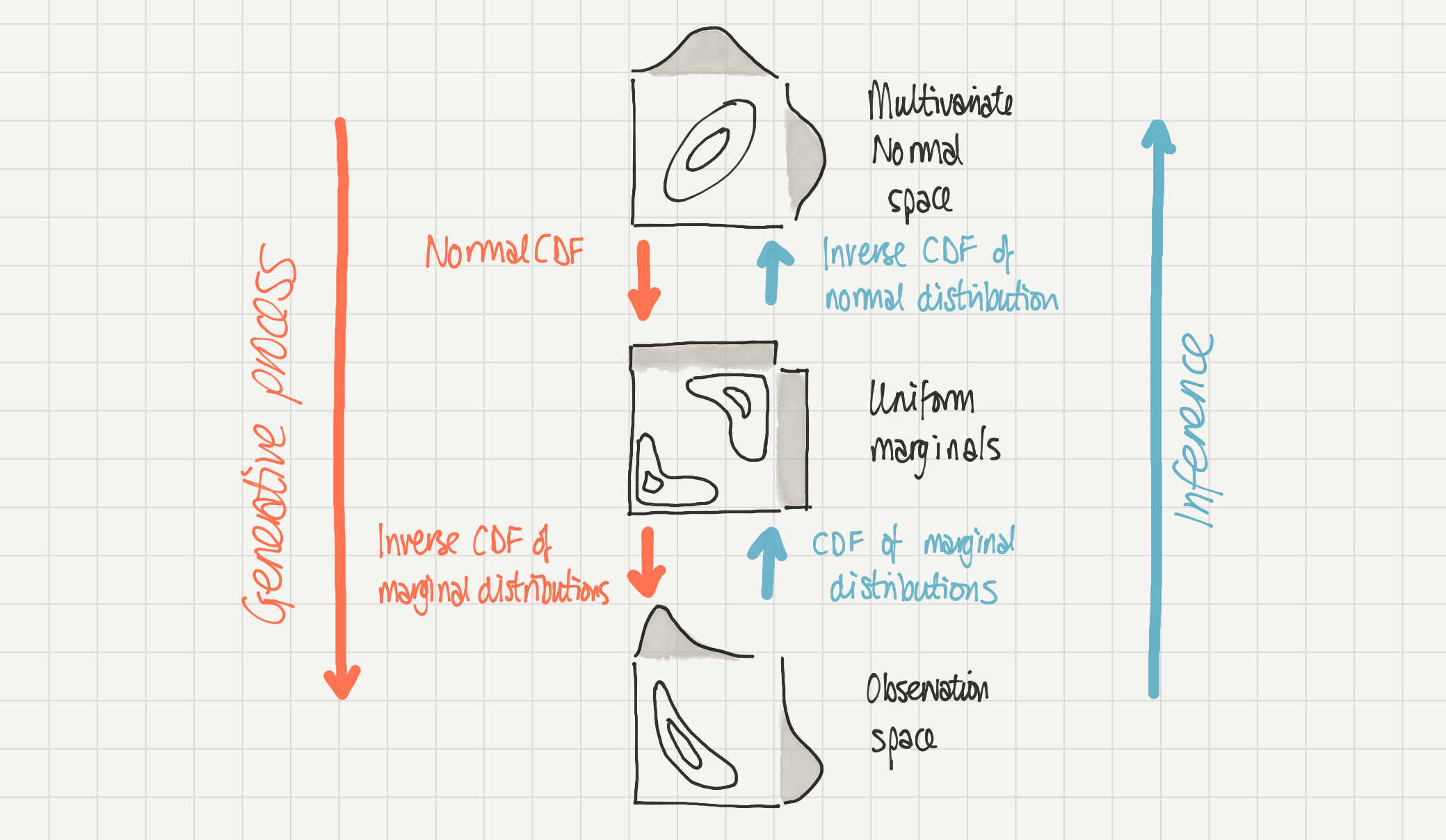
二维高斯Copula的示意图。我们在观测空间中的复杂分布P(a, b)（底部）被建模为由多元正态空间中的二维高斯Copula生成（顶部）。从多元正态空间到观测空间的映射（向下）是通过正态累积密度函数，然后是边缘分布的逆累积密度函数完成的。相反，推理过程（向上）可以通过边缘分布的累积密度函数，然后是正态分布的逆累积密度函数来完成。

本笔记本将描述如何基于具有丰富相关结构的双变量数据对copulas进行推断。我们PyMC Labs作为与Gates Foundation更大项目的一部分完成了这项工作，其中一些内容也在这里进行了概述。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import pytensor.tensor as pt
import seaborn as sns

from scipy.stats import expon, multivariate_normal, norm

%config InlineBackend.figure_format = 'retina'
az.style.use("arviz-darkgrid")
plt.rcParams.update({"font.size": 14, "figure.constrained_layout.use": False})
SEED = 43
rng = np.random.default_rng(SEED)

数据生成过程

在深入推理之前，我们将花一些时间详细说明上述示意图中的步骤。首先，我们将通过描述多元正态copula并将其转换到观测空间来演示生成模型。其次，我们展示如何通过逆变换从观测空间返回到多元正态空间。一旦我们确定了这些细节，我们将在后面的部分继续进行推理过程。

现在我们将使用嵌套字典定义我们的高斯copula的属性。在顶层，我们有键 a 和 b 以及 rho。

• rho 描述了多元正态copula的相关系数。

• a 和 b 也是字典，每个字典包含边缘分布（作为 scipy 分布对象）及其参数。

请注意，我们隐含地定义多元正态分布具有零均值和单位方差。这是因为这些矩在通过“均匀空间”的变换中不会保留，这是我们上面copula示意图中的第二步。

# define properties of our copula
b_scale = 2
θ = {"a_dist": norm(), "b_dist": expon(scale=1 / b_scale), "rho": 0.9}

首先，我们定义真实的多元正态分布并从中抽取一些样本。

n_samples = 5000

# draw random samples in multivariate normal space
mu = [0, 0]
cov = [[1, θ["rho"]], [θ["rho"], 1]]
x = multivariate_normal(mu, cov).rvs(n_samples, random_state=rng)
a_norm = x[:, 0]
b_norm = x[:, 1]

sns.jointplot(x=a_norm, y=b_norm, height=6, kind="hex");

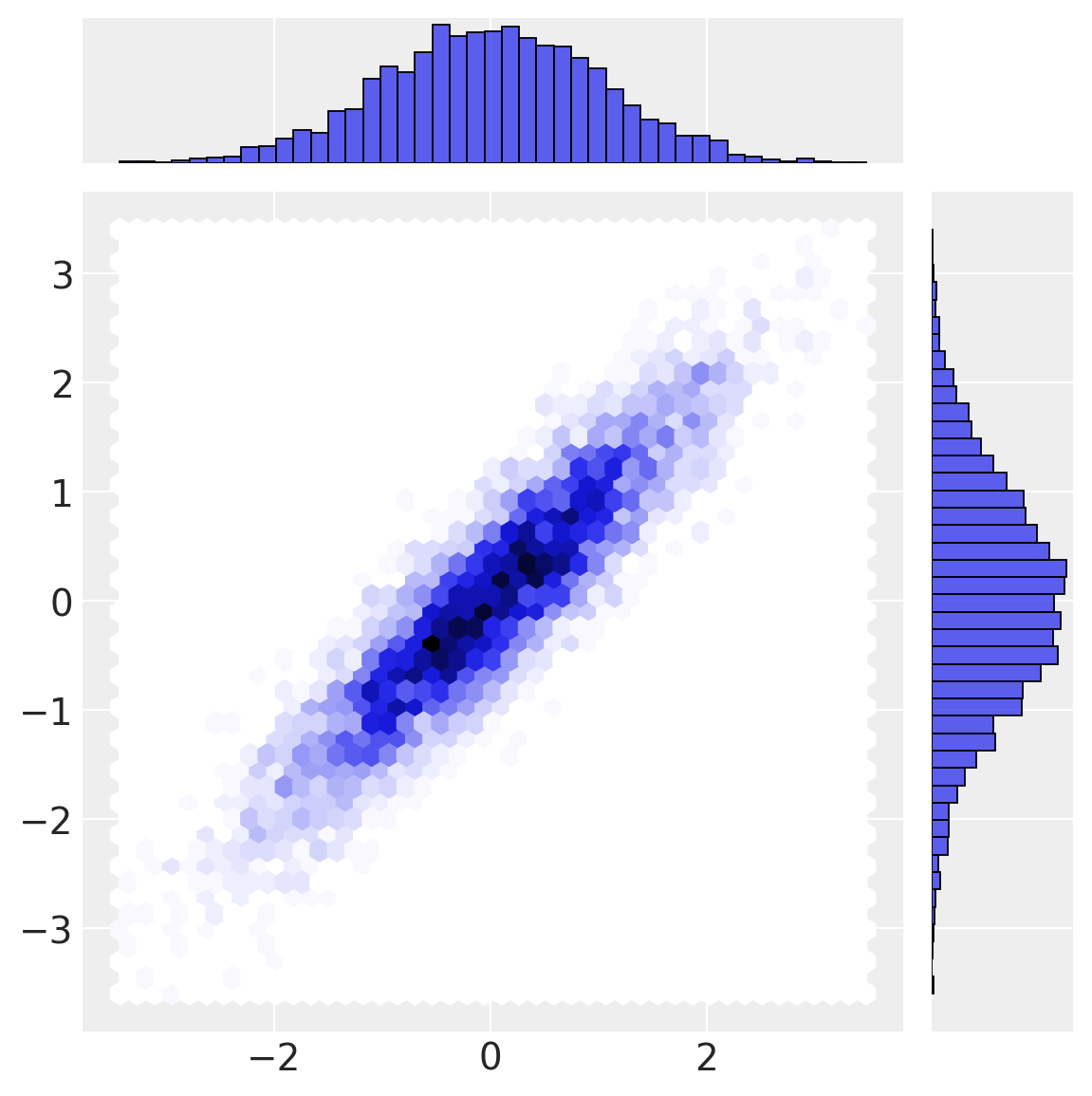
我们的第一个变换（正态累积分布函数）将数据从多元正态空间转换为均匀空间。注意边缘分布是如何均匀的，但多元正态空间中的相关结构仍然保留在下面的有趣联合密度中。

# make marginals uniform
a_unif = norm(loc=0, scale=1).cdf(a_norm)
b_unif = norm(loc=0, scale=1).cdf(b_norm)
sns.jointplot(x=a_unif, y=b_unif, height=6, kind="hex");

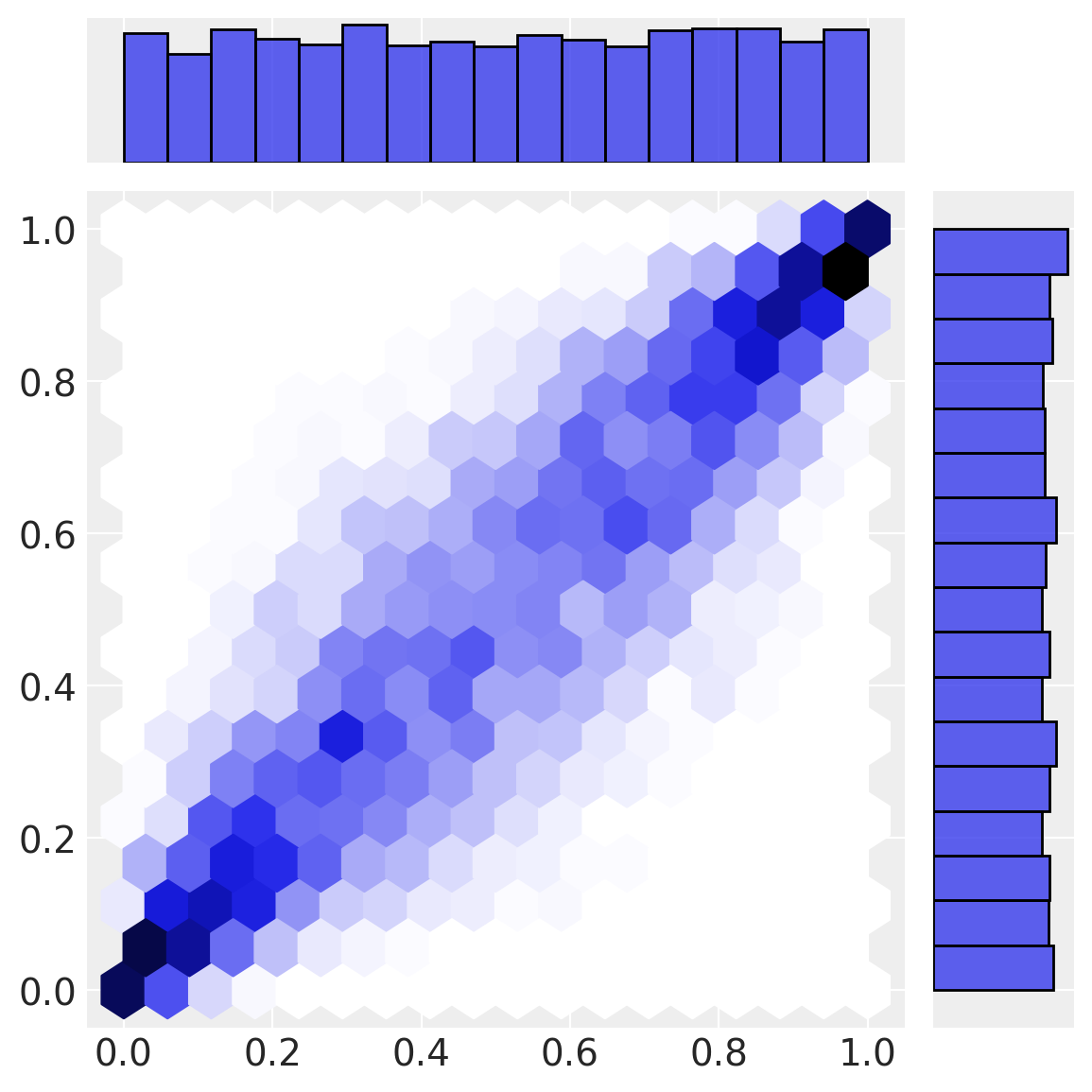
我们的最终变换（边缘分布的逆CDF）在观测空间中产生了\(a\)和\(b\)。

# transform to observation space
a = θ["a_dist"].ppf(a_unif)
b = θ["b_dist"].ppf(b_unif)
sns.jointplot(x=a, y=b, height=6, kind="hex", xlim=(-4, 4), ylim=(0, 3));

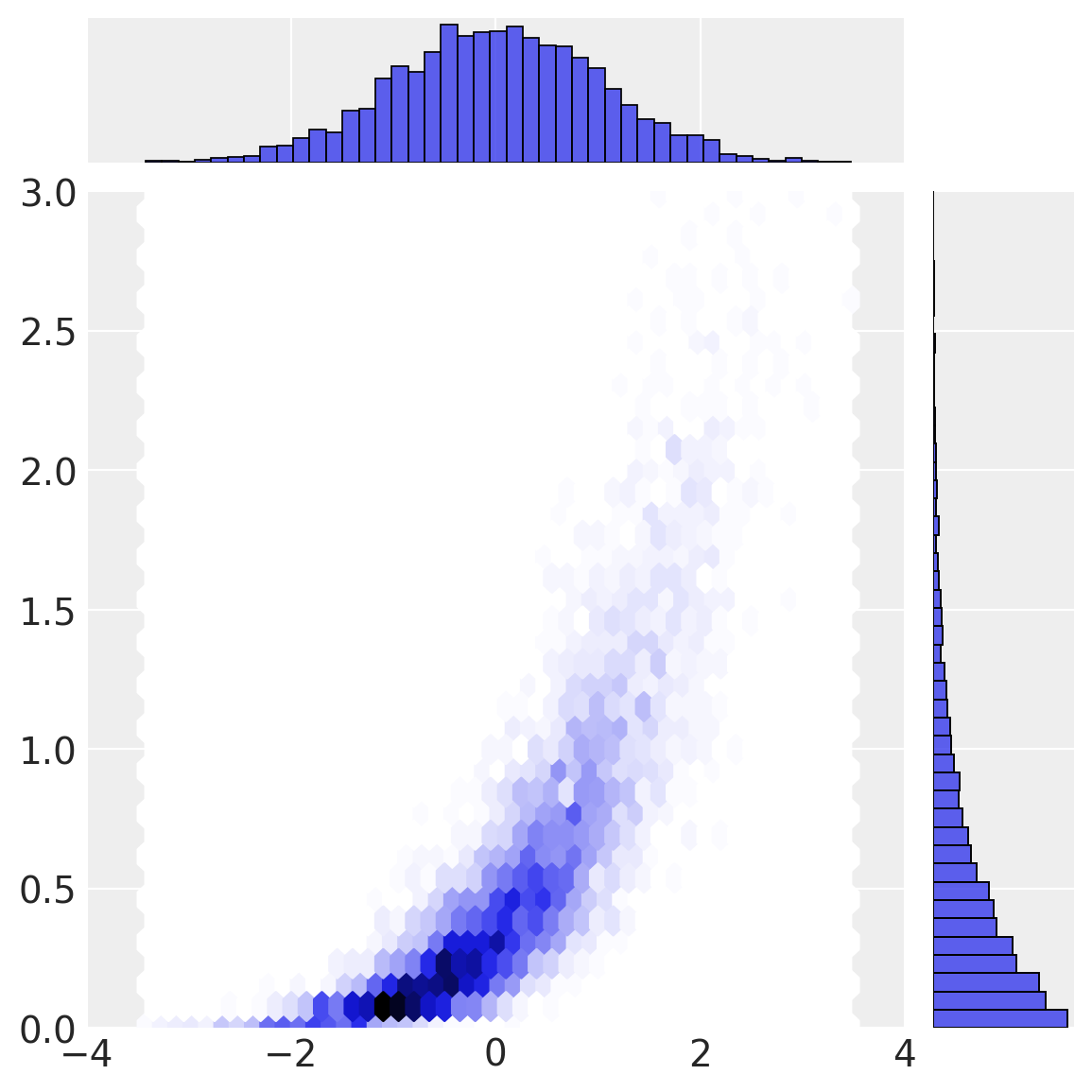
Copula推断过程

为了理解所采用的方法，我们将逐步介绍逆过程，从观测空间到多元正态空间。

# observation -> uniform space
a1 = θ["a_dist"].cdf(a)
b1 = θ["b_dist"].cdf(b)
sns.jointplot(x=a1, y=b1, kind="hex", height=6);

# uniform -> MvNormal space
a2 = norm(loc=0, scale=1).ppf(a1)
b2 = norm(loc=0, scale=1).ppf(b1)
sns.jointplot(x=a2, y=b2, kind="hex", height=6);

所以现在我们已经完成了我们在图1中概述的内容。我们详细地逐步介绍了从多元正态分布到观测空间的数据生成过程。然后我们看到了如何进行逆过程（推理），从观测空间回到多元正态分布空间。这是我们在PyMC模型中使用的方法。

用于联合分布和边缘分布估计的PyMC模型

我们将在多元正态空间中对参数进行推断，通过观测空间中的数据来约束合理的参数值。然而，我们还利用对\(a\)和\(b\)的观测来约束边缘分布参数的估计。

在我们的实验中，我们探索了同时估计边缘参数和copula协方差参数的模型，但我们发现这种方法不稳定。我们下面使用的解决方案被发现更为稳健，并且涉及一个两步过程。

1. 估计边缘分布的参数。

2. 估计copula的协方差参数，使用步骤1中边缘分布参数的点估计。

coords = {"obs_id": np.arange(len(a))}
with pm.Model(coords=coords) as marginal_model:
    """
    Assumes observed data in variables `a` and `b`
    """
    # marginal estimation
    a_mu = pm.Normal("a_mu", mu=0, sigma=1)
    a_sigma = pm.Exponential("a_sigma", lam=0.5)
    pm.Normal("a", mu=a_mu, sigma=a_sigma, observed=a, dims="obs_id")

    b_scale = pm.Exponential("b_scale", lam=0.5)
    pm.Exponential("b", lam=1 / b_scale, observed=b, dims="obs_id")

pm.model_graph.model_to_graphviz(marginal_model)

with marginal_model:
    marginal_idata = pm.sample(random_seed=rng)

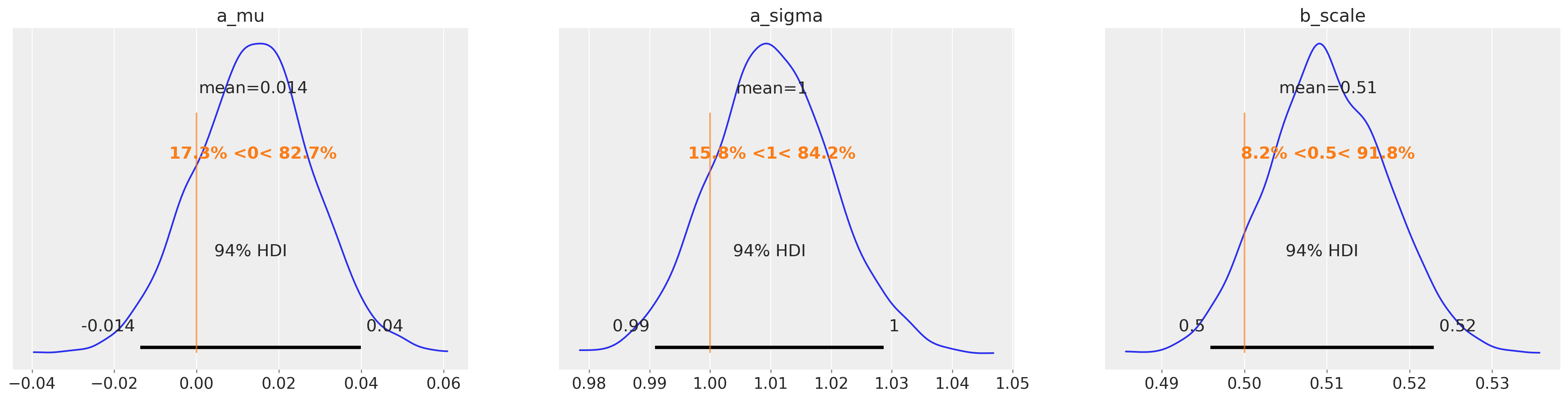
az.plot_posterior(
    marginal_idata, var_names=["a_mu", "a_sigma", "b_scale"], ref_val=[0, 1.0, 1 / 2.0]
);

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a_mu, a_sigma, b_scale]

100.00% [8000/8000 00:01<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 seconds.

在下面的copula模型中，您可以看到我们为协方差参数设置了一个先验。该参数的后验分布受多元正态空间中数据的约束。但为了做到这一点，我们需要将观测空间中的观测值 [a, b] 转换为多元正态空间，我们将其存储在 data 中。

在使用点估计时：正如您将在下面的代码中看到的，我们选择使用步骤1的点估计，而不是步骤1的完整后验分布。这是由于在将后验分布作为参数传递给分布时，处理张量形状的复杂性，我们选择进行简化。

然而，在笔记本审查期间，@OriolAbril（PyMC 示例仓库的维护者之一）正确指出，对在分布下评估的数据点的 logcdf 进行指数运算，使用点估计 并不一定会 返回等于在许多可能的分布（从完整后验构建）下评估的数据点的 logcdf 的指数期望值。为了确保笔记本的及时进展，我们选择按原样展示代码，但也留下此注释，以便我们未来的自己稍后更新笔记本，同时也为未来的读者提供通过修改示例来解决此问题的机会。

def transform_data(marginal_idata):
    # point estimates
    a_mu = marginal_idata.posterior["a_mu"].mean().item()
    a_sigma = marginal_idata.posterior["a_sigma"].mean().item()
    b_scale = marginal_idata.posterior["b_scale"].mean().item()
    # transformations from observation space -> uniform space
    __a = pt.exp(pm.logcdf(pm.Normal.dist(mu=a_mu, sigma=a_sigma), a))
    __b = pt.exp(pm.logcdf(pm.Exponential.dist(lam=1 / b_scale), b))
    # uniform space -> multivariate normal space
    _a = pm.math.probit(__a)
    _b = pm.math.probit(__b)
    # join into an Nx2 matrix
    data = pt.math.stack([_a, _b], axis=1).eval()
    return data, a_mu, a_sigma, b_scale


data, a_mu, a_sigma, b_scale = transform_data(marginal_idata)

coords.update({"param": ["a", "b"], "param_bis": ["a", "b"]})
with pm.Model(coords=coords) as copula_model:
    # Prior on covariance of the multivariate normal
    chol, corr, stds = pm.LKJCholeskyCov(
        "chol",
        n=2,
        eta=2.0,
        sd_dist=pm.Exponential.dist(1.0),
        compute_corr=True,
    )
    cov = pm.Deterministic("cov", chol.dot(chol.T), dims=("param", "param_bis"))

    # Likelihood function
    pm.MvNormal("N", mu=0.0, cov=cov, observed=data, dims=("obs_id", "param"))

pm.model_graph.model_to_graphviz(copula_model)

with copula_model:
    copula_idata = pm.sample(random_seed=rng, tune=2000, cores=1)

az.plot_posterior(copula_idata, var_names=["cov"], ref_val=[1.0, θ["rho"], θ["rho"], 1.0]);

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Sequential sampling (2 chains in 1 job)
NUTS: [chol]

100.00% [3000/3000 00:03<00:00 Sampling chain 0, 0 divergences]

/Users/benjamv/opt/mambaforge/envs/pymc_env/lib/python3.11/site-packages/pytensor/compile/function/types.py:970: RuntimeWarning: invalid value encountered in accumulate
  self.vm()

100.00% [3000/3000 00:03<00:00 Sampling chain 1, 0 divergences]

Sampling 2 chains for 2_000 tune and 1_000 draw iterations (4_000 + 2_000 draws total) took 7 seconds.
We recommend running at least 4 chains for robust computation of convergence diagnostics

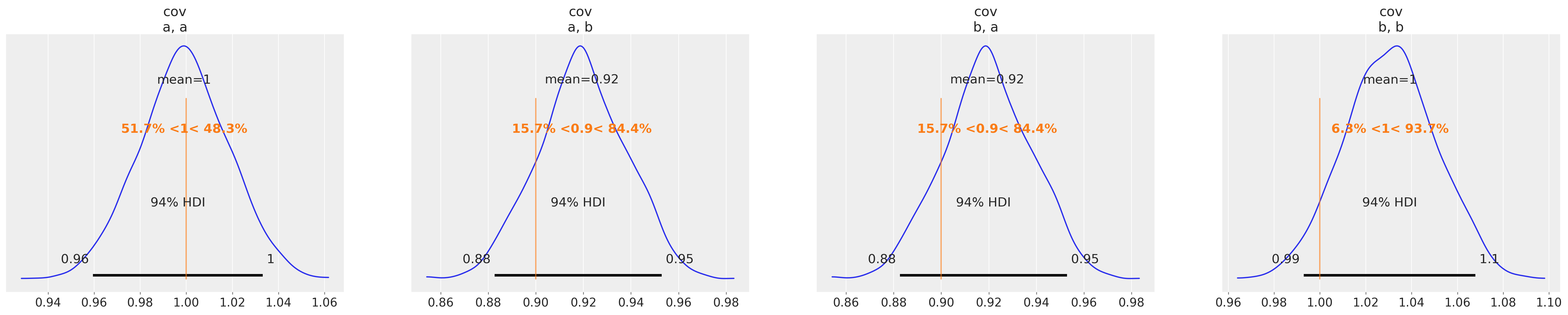
你可以看到，我们已经成功恢复了用于生成样本数据的多变量正态copula的协方差矩阵。

在下面的部分中，我们将使用这些信息来从我们的参数描述中进行采样，该描述涉及\(P(a, b)\)。

将推断结果与真实数据进行比较

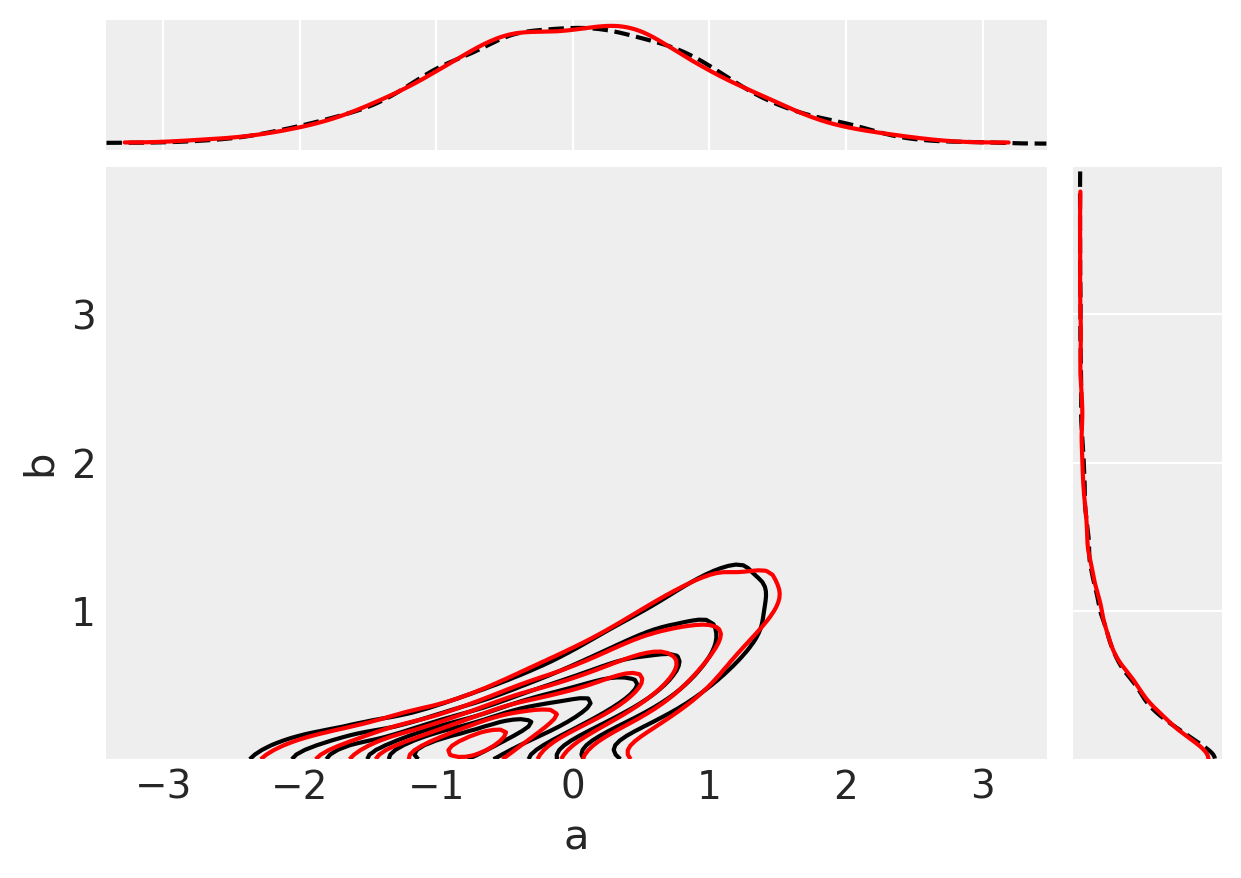
最后，我们可以进行视觉检查，看看我们的推断（红色）是否与原始观测数据（黑色）相符。

# data munging to extract covariance estimates from copula_idata in useful shape
d = {k: v.values.reshape((-1, *v.shape[2:])) for k, v in copula_idata.posterior[["cov"]].items()}

# generate (a, b) samples
ab = np.vstack([multivariate_normal([0, 0], cov).rvs() for cov in d["cov"]])

# transform to uniform space
uniform_a = norm().cdf(ab[:, 0])
uniform_b = norm().cdf(ab[:, 1])

# transform to observation space
# estimated marginal parameters a_mu, a_sigma, b_scale are point estimates from marginal estimation.
ppc_a = norm(loc=a_mu, scale=a_sigma).ppf(uniform_a)
ppc_b = expon(scale=b_scale).ppf(uniform_b)

# plot data in black
ax = az.plot_pair(
    {"a": a, "b": b},
    marginals=True,
    # kind=["kde", "scatter"],
    kind="kde",
    scatter_kwargs={"alpha": 0.1},
    kde_kwargs=dict(
        contour_kwargs=dict(colors="k", linestyles="--"), contourf_kwargs=dict(alpha=0)
    ),
    marginal_kwargs=dict(color="k", plot_kwargs=dict(ls="--")),
)

# plot inferences in red
axs = az.plot_pair(
    {"a": ppc_a, "b": ppc_b},
    marginals=True,
    # kind=["kde", "scatter"],
    kind="kde",
    scatter_kwargs={"alpha": 0.01},
    kde_kwargs=dict(contour_kwargs=dict(colors="r", linestyles="-"), contourf_kwargs=dict(alpha=0)),
    marginal_kwargs=dict(color="r"),
    ax=ax,
);

/Users/benjamv/opt/mambaforge/envs/pymc_env/lib/python3.11/site-packages/arviz/plots/backends/matplotlib/kdeplot.py:166: UserWarning: The following kwargs were not used by contour: 'linestyle'
  qcs = ax.contour(x_x, y_y, density, **contour_kwargs)

致谢

我们要感谢Jonathan Sedar、Junpeng Lao和Oriol Abril在本笔记本开发过程中提供的宝贵建议。

作者

• 由 Eric Ma 和 Benjamin T. Vincent 于2023年11月撰写（pymc-examples#257）。

水印

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray

Last updated: Mon Dec 04 2023

Python implementation: CPython
Python version       : 3.11.6
IPython version      : 8.18.1

pytensor: 2.18.1
xarray  : 2023.11.0

arviz     : 0.16.1
pymc      : 5.10.0
seaborn   : 0.13.0
matplotlib: 3.8.2
numpy     : 1.26.2
pytensor  : 2.18.1

Watermark: 2.4.3

许可证声明

本示例库中的所有笔记本均在MIT许可证下提供，该许可证允许修改和重新分发，前提是保留版权和许可证声明。

引用 PyMC 示例

要引用此笔记本，请使用Zenodo为pymc-examples仓库提供的DOI。

重要

许多笔记本是从其他来源改编的：博客、书籍……在这种情况下，您应该引用原始来源。

同时记得引用代码中使用的相关库。

这是一个BibTeX的引用模板：

@incollection{citekey,
  author    = "<notebook authors, see above>",
  title     = "<notebook title>",
  editor    = "PyMC Team",
  booktitle = "PyMC examples",
  doi       = "10.5281/zenodo.5654871"
}

渲染后可能看起来像：