多项式混合的狄利克雷分布#
这个示例笔记本演示了使用狄利克雷多项式混合模型(也称为狄利克雷-多项式分布或DM)来建模分类计数数据。像这样的模型在包括自然语言处理、生态学、生物信息学等多个领域中都非常重要。
狄利克雷-多项分布可以理解为从多项分布中抽取的样本,其中每个样本具有略微不同的概率向量,该向量本身是从一个共同的狄利克雷分布中抽取的。这与多项分布形成对比,后者假设所有观测值都来自一个固定的单一概率向量。这使得狄利克雷-多项分布能够适应比多项分布更具变异性(也称为过度分散)的计数数据。
过度分散的计数分布的其他例子包括 Beta-二项分布 (可以被视为DM的特殊情况)或 负二项分布。
DM 也是对混合分布在其潜在参数上进行边缘化的一个例子。 本笔记本将展示采用这种方法所带来的性能优势。
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import scipy as sp
print(f"Running on PyMC v{pm.__version__}")
Running on PyMC v5.9.0
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
模拟数据#
让我们为这个例子模拟一些过度分散的分类计数数据。
这里我们正在从DM分布本身进行模拟, 所以拟合该模型可能显得有些同义反复, 但请放心,类似这样的数据确实会出现在 不同计数中:
文本语料库中的词语 [],
细胞中的RNA分子类型 [],
购物者购买的商品 []。
这里我们将讨论一个社区生态学的例子,假设我们观察了\(k=5\)种不同的树种在\(n=10\)个不同的森林中的数量。
我们的模拟将生成一个二维整数矩阵(计数),其中每一行(从零开始索引)由 \(i \in (0...n-1)\) 表示,是一个观测值(不同的森林),每一列 \(j \in (0...k-1)\) 是一个类别(树种)。我们将用三个参数来参数化这个分布:
\(\mathrm{frac}\) : 每个物种的预期比例, 一个在单纯形上的 \(k\)-维向量(即总和为一)
\(\mathrm{total\_count}\) : 每个观测中统计的项目总数,
\(\mathrm{conc}\) : 浓度,控制我们数据的过度分散, 其中较大的值使得我们的分布更接近多项分布。
在这里,以及在整个笔记本中,我们使用了一个 方便的重参数化 狄利克雷分布 从一个到两个参数, \(\alpha=\mathrm{conc} \times \mathrm{frac}\),因为这符合我们的期望解释。
每个来自DM的观测值通过以下方式模拟:
首先在 \(k\)-单纯形上获得一个值,模拟为 \(p_i \sim \mathrm{Dirichlet}(\alpha=\mathrm{conc} \times \mathrm{frac})\),
然后模拟 \(\mathrm{counts}_i \sim \mathrm{Multinomial}(\mathrm{total\_count}, p_i)\)。
请注意,每个观测值都有其自身的潜在参数 \(p_i\),这些参数是独立地从一个共同的狄利克雷分布中模拟出来的。
true_conc = 6.0
true_frac = np.array([0.45, 0.30, 0.15, 0.09, 0.01])
trees = ["pine", "oak", "ebony", "rosewood", "mahogany"] # Tree species observed
# fmt: off
forests = [ # Forests observed
"sunderbans", "amazon", "arashiyama", "trossachs", "valdivian",
"bosc de poblet", "font groga", "monteverde", "primorye", "daintree",
]
# fmt: on
k = len(trees)
n = len(forests)
total_count = 50
true_p = sp.stats.dirichlet(true_conc * true_frac).rvs(size=n, random_state=rng)
observed_counts = np.vstack(
[sp.stats.multinomial(n=total_count, p=p_i).rvs(random_state=rng) for p_i in true_p]
)
observed_counts
array([[21, 9, 11, 6, 3],
[36, 7, 6, 1, 0],
[ 8, 31, 1, 10, 0],
[25, 4, 17, 4, 0],
[43, 6, 1, 0, 0],
[28, 10, 12, 0, 0],
[21, 16, 10, 3, 0],
[16, 32, 2, 0, 0],
[45, 4, 1, 0, 0],
[35, 5, 2, 8, 0]])
多项式模型#
我们将拟合到这些数据的第一个模型是一个简单的多项式模型,其中唯一的参数是每个类别的预期比例,\(\mathrm{frac}\),我们将为其赋予一个狄利克雷先验。 虽然均匀先验(\(\alpha_j=1\) 对于每个 \(j\))效果良好,但如果我们对每种树的比例有独立的信念, 我们可以将此编码到我们的先验中,例如,在我们预期物种比例较高的地方增加 \(\alpha_j\) 的值。
coords = {"tree": trees, "forest": forests}
with pm.Model(coords=coords) as model_multinomial:
frac = pm.Dirichlet("frac", a=np.ones(k), dims="tree")
counts = pm.Multinomial(
"counts", n=total_count, p=frac, observed=observed_counts, dims=("forest", "tree")
)
pm.model_to_graphviz(model_multinomial)
with model_multinomial:
trace_multinomial = pm.sample(chains=4)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [frac]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.
az.plot_trace(data=trace_multinomial, var_names=["frac"]);

轨迹图看起来相当不错;从视觉上看,每个参数似乎都在后验分布中良好地移动。
summary_multinomial = az.summary(trace_multinomial, var_names=["frac"])
summary_multinomial = summary_multinomial.assign(
ess_bulk_per_sec=lambda x: x.ess_bulk / trace_multinomial.posterior.sampling_time,
)
summary_multinomial
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | ess_bulk_per_sec | |
|---|---|---|---|---|---|---|---|---|---|---|
| frac[pine] | 0.552 | 0.022 | 0.510 | 0.591 | 0.0 | 0.0 | 5955.0 | 3480.0 | 1.0 | 2675.351076 |
| frac[oak] | 0.248 | 0.019 | 0.213 | 0.284 | 0.0 | 0.0 | 5428.0 | 3478.0 | 1.0 | 2438.590368 |
| frac[ebony] | 0.127 | 0.015 | 0.099 | 0.153 | 0.0 | 0.0 | 4773.0 | 3080.0 | 1.0 | 2144.324212 |
| frac[rosewood] | 0.065 | 0.011 | 0.045 | 0.086 | 0.0 | 0.0 | 3351.0 | 2680.0 | 1.0 | 1505.474636 |
| frac[mahogany] | 0.008 | 0.004 | 0.001 | 0.015 | 0.0 | 0.0 | 1341.0 | 1277.0 | 1.0 | 602.459411 |
同样,参数汇总表中的诊断结果看起来都正常。 这里我们增加了一列,用于估计每秒采样的有效样本量。
az.plot_forest(trace_multinomial, var_names=["frac"])
for j, (y_tick, frac_j) in enumerate(zip(plt.gca().get_yticks(), reversed(true_frac))):
plt.vlines(frac_j, ymin=y_tick - 0.45, ymax=y_tick + 0.45, color="black", linestyle="--")
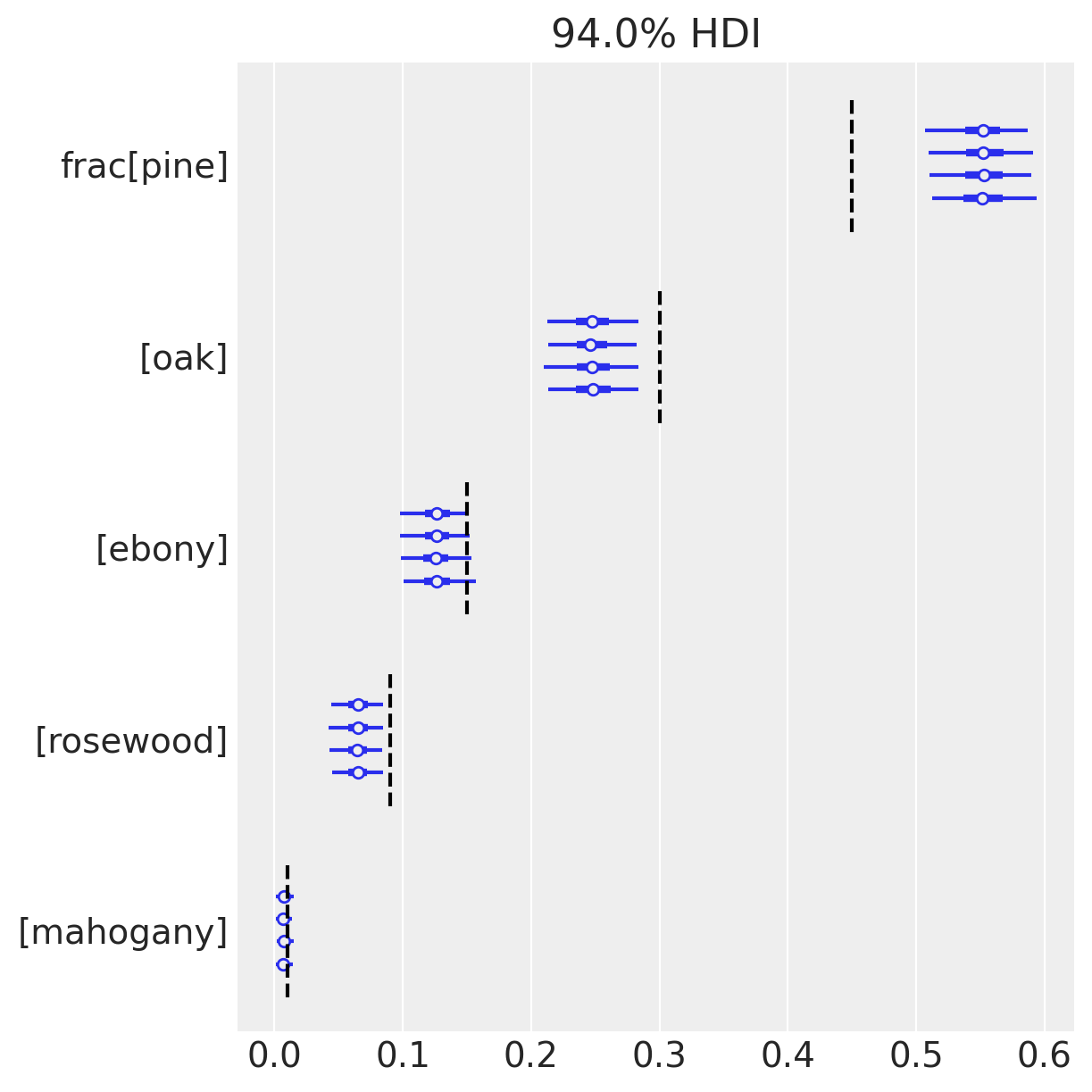
这里我们绘制了一个森林图,展示了我们后验近似的均值和94% HDI。 有趣的是,因为我们知道每个物种的基础频率(虚线),我们可以评论我们推断的准确性。 现在我们模型的问题变得明显了; 注意到94% HDI 不包括树种0、1、3的真实值。 我们可能看到一个 HDI错过,但三个???
…发生了什么?
让我们使用后验预测检查来排查这个模型的问题,比较我们的数据与基于后验估计的模拟数据。
with model_multinomial:
pp_samples = pm.sample_posterior_predictive(trace=trace_multinomial)
# Concatenate with InferenceData object
trace_multinomial.extend(pp_samples)
Sampling: [counts]
cmap = plt.get_cmap("tab10")
fig, axs = plt.subplots(k, 1, sharex=True, sharey=True, figsize=(6, 8))
for j, ax in enumerate(axs):
c = cmap(j)
ax.hist(
trace_multinomial.posterior_predictive.counts.sel(tree=trees[j]).values.flatten(),
bins=np.arange(total_count),
histtype="step",
color=c,
density=True,
label="Post.Pred.",
)
ax.hist(
(trace_multinomial.observed_data.counts.sel(tree=trees[j]).values.flatten()),
bins=np.arange(total_count),
color=c,
density=True,
alpha=0.25,
label="Observed",
)
ax.axvline(
true_frac[j] * total_count,
color=c,
lw=1.0,
alpha=0.45,
label="True",
)
ax.annotate(
f"{trees[j]}",
xy=(0.96, 0.9),
xycoords="axes fraction",
ha="right",
va="top",
color=c,
)
axs[-1].legend(loc="upper center", fontsize=10)
axs[-1].set_xlabel("Count")
axs[-1].set_yticks([0, 0.5, 1.0])
axs[-1].set_ylim(0, 0.6);
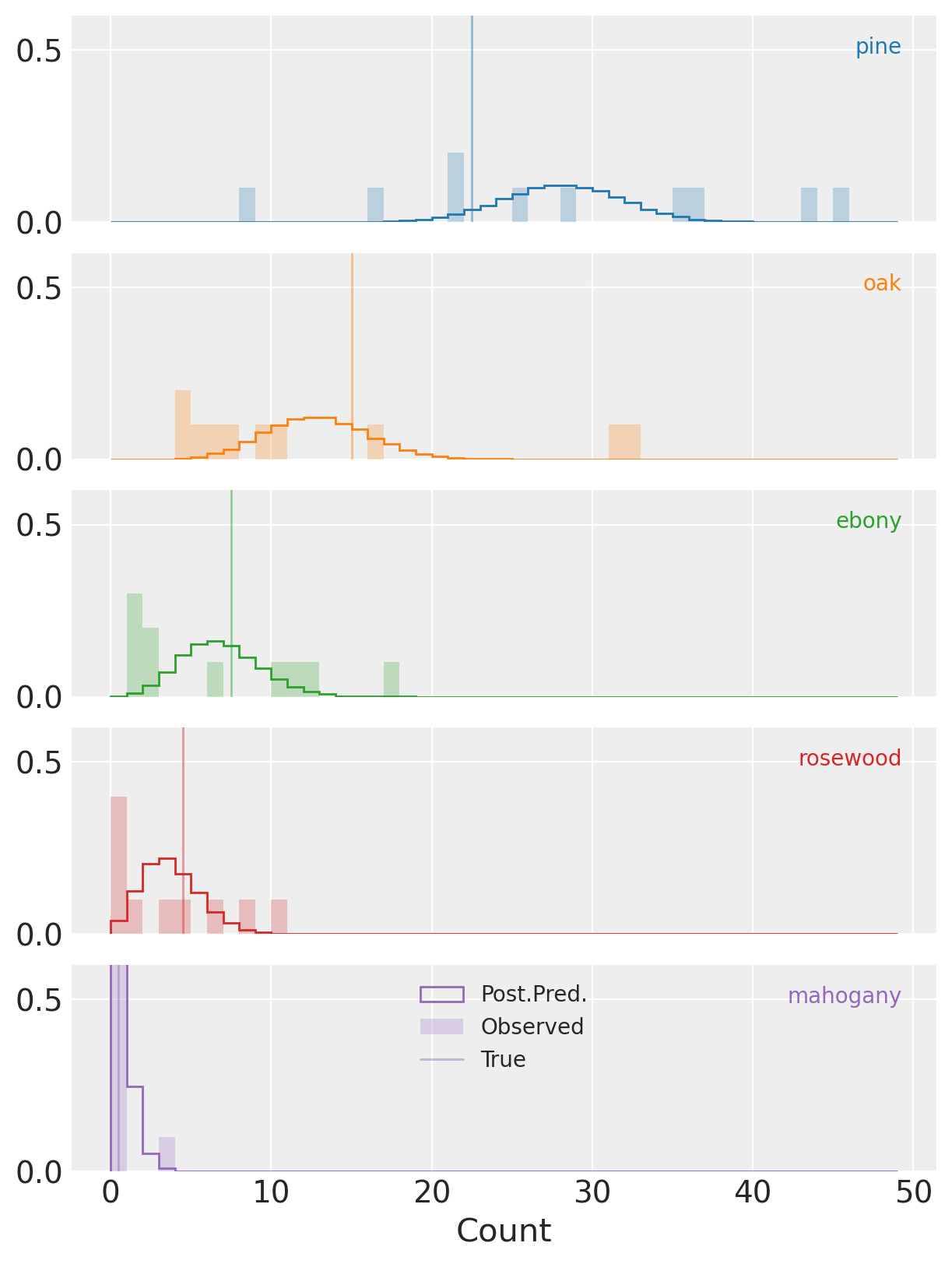
这里我们绘制了每个物种的预测计数与观测计数的直方图。
(注意,y轴没有完全显示高度,并且剪切了紫色中桃花心木物种的分布。)
现在我们可以开始理解为什么我们的后验HDI与五个物种中的三个物种的真实参数(垂直线)有所偏离。
可以看到,对于所有物种,观察到的计数经常与基于后验分布的预测相差甚远。
这一点在(例如)oak中尤为明显,尽管后验预测质量集中在远低于此的数值上,但我们有一个超过30棵该物种树木的观察记录。
这是过度离散在工作,并且是一个明确的信号,表明我们需要调整模型以适应它。
后验预测检查是诊断模型错误指定的一种最佳方法,这个例子也不例外。
Dirichlet-多项式模型 - 显式混合#
让我们继续使用DM分布对我们的数据进行建模。
对于这个模型,我们将保持每个物种预期频率的相同先验,\(\mathrm{frac}\)。我们还将添加一个严格为正的参数,\(\mathrm{conc}\),用于浓度。
在本次模型迭代中,我们将明确包含潜在的多项式概率,\(p_i\),模拟我们的\(\mathrm{true\_p}_i\)(在现实世界中我们无法观察到)。
with pm.Model(coords=coords) as model_dm_explicit:
frac = pm.Dirichlet("frac", a=np.ones(k), dims="tree")
conc = pm.Lognormal("conc", mu=1, sigma=1)
p = pm.Dirichlet("p", a=frac * conc, dims=("forest", "tree"))
counts = pm.Multinomial(
"counts", n=total_count, p=p, observed=observed_counts, dims=("forest", "tree")
)
pm.model_to_graphviz(model_dm_explicit)
将此图与第一个图进行比较。 这里,潜在的、狄利克雷分布的 \(p\) 将多项式与期望频率 \(\mathrm{frac}\) 分隔开, 解释了相对于简单多项式模型的计数过度分散。
with model_dm_explicit:
trace_dm_explicit = pm.sample(chains=4, target_accept=0.9)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [frac, conc, p]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 87 seconds.
The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details
The effective sample size per chain is smaller than 100 for some parameters. A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details
There were 16 divergences after tuning. Increase `target_accept` or reparameterize.
在这里,我们不得不将target_accept从0.8增加到0.9,以避免被分歧淹没。
我们还收到了关于rhat统计量的警告,尽管我们现在暂时忽略它。
更有趣的是,与第一个模型相比,采样这个模型花费了更长的时间。
这部分是因为我们的模型有额外的约\((n \times k)\)个参数,
但似乎NUTS还面临其他几何上的挑战。
我们将在下一个模型中看看是否能修复这些问题,但目前我们先来看看这些追踪信息。
az.plot_trace(data=trace_dm_explicit, var_names=["frac", "conc"]);
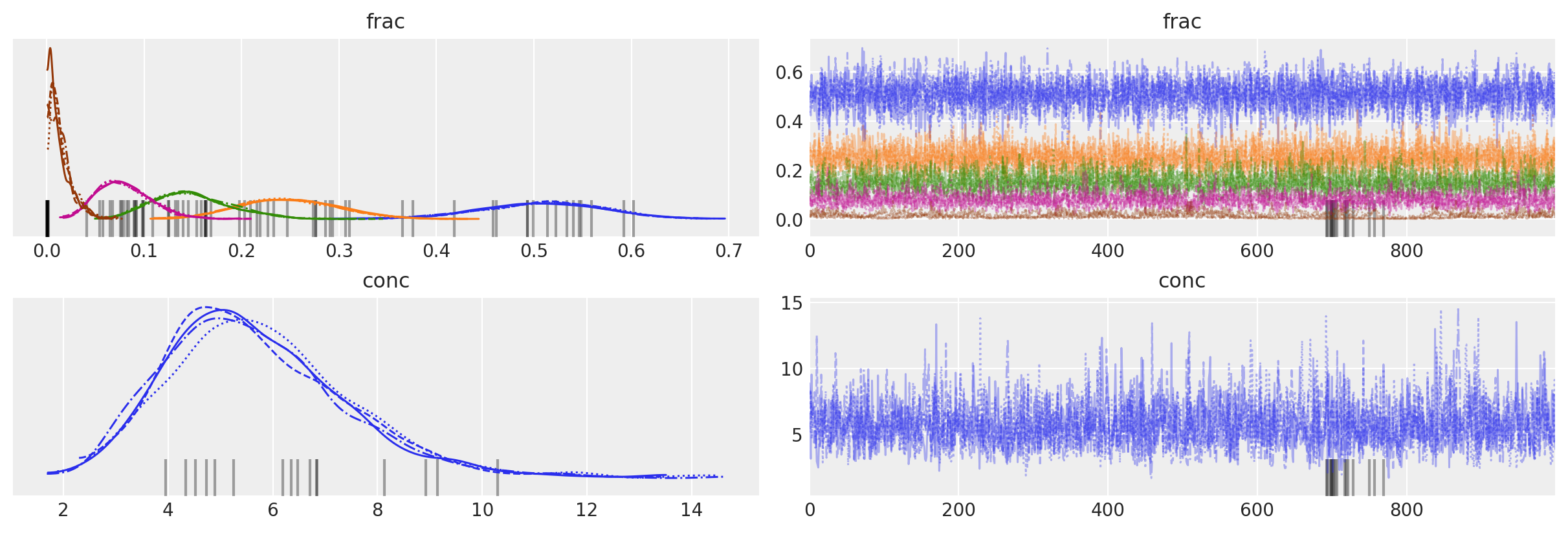
当稀有物种(mahogany)的估计比例非常接近零时,分歧似乎会发生。
az.plot_forest(trace_dm_explicit, var_names=["frac"])
for j, (y_tick, frac_j) in enumerate(zip(plt.gca().get_yticks(), reversed(true_frac))):
plt.vlines(frac_j, ymin=y_tick - 0.45, ymax=y_tick + 0.45, color="black", linestyle="--")
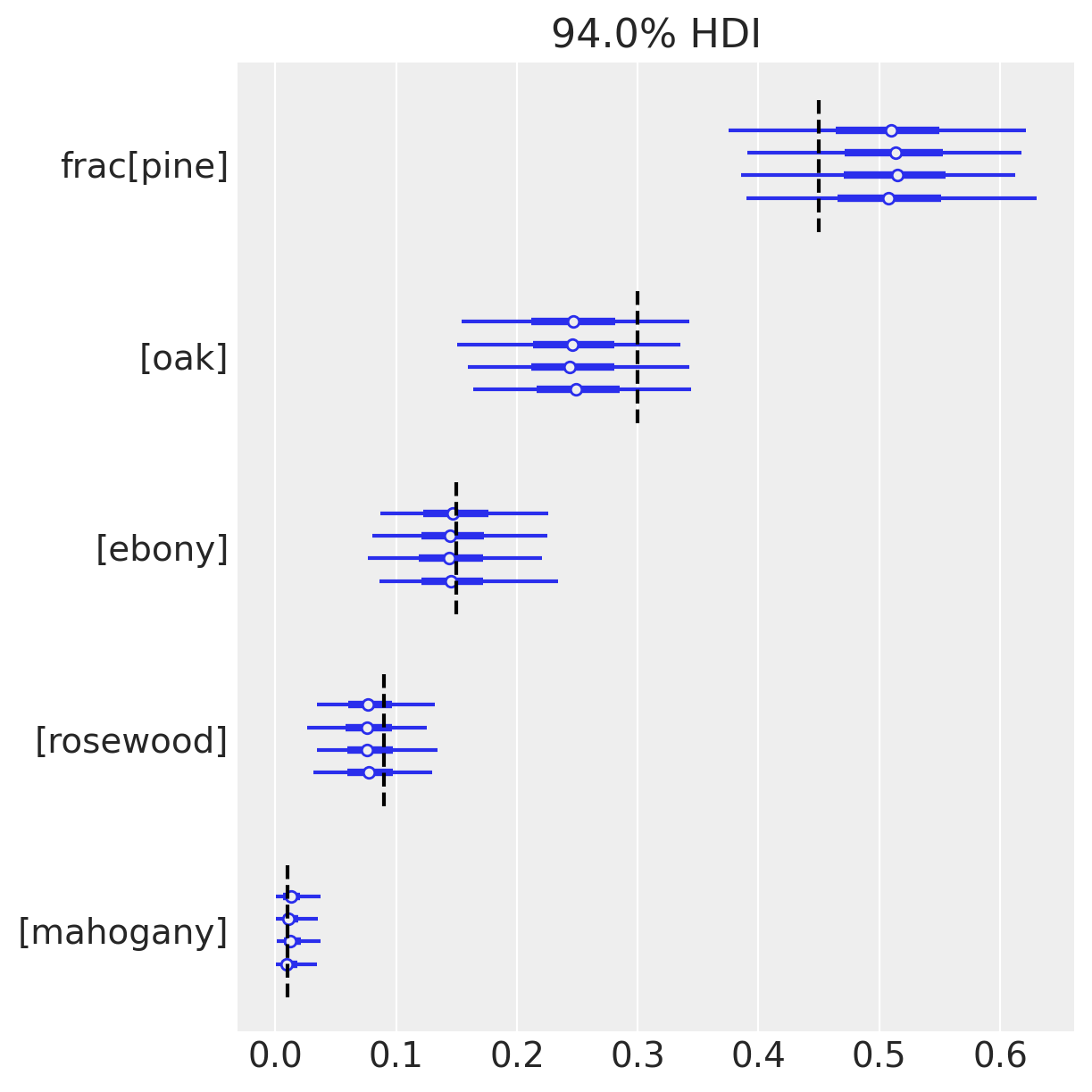
另一方面,由于我们知道\(\mathrm{frac}\)的地面真实值, 我们可以为自己感到高兴, 因为HDI包含了所有物种的真实值!
建模这种混合分布使我们的推断对计数的过度离散性具有鲁棒性,而普通的多项分布则非常敏感。 请注意,每个\(\mathrm{frac}_i\)的HDI比之前宽得多。 在这种情况下,这使得推断的正确与错误之间产生了差异。
summary_dm_explicit = az.summary(trace_dm_explicit, var_names=["frac", "conc"])
summary_dm_explicit = summary_dm_explicit.assign(
ess_bulk_per_sec=lambda x: x.ess_bulk / trace_dm_explicit.posterior.sampling_time,
)
summary_dm_explicit
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | ess_bulk_per_sec | |
|---|---|---|---|---|---|---|---|---|---|---|
| frac[pine] | 0.509 | 0.063 | 0.386 | 0.622 | 0.001 | 0.001 | 4102.0 | 3040.0 | 1.00 | 47.028042 |
| frac[oak] | 0.248 | 0.050 | 0.158 | 0.343 | 0.001 | 0.000 | 5036.0 | 2996.0 | 1.00 | 57.736036 |
| frac[ebony] | 0.149 | 0.040 | 0.082 | 0.227 | 0.001 | 0.000 | 3379.0 | 2915.0 | 1.00 | 38.739091 |
| frac[rosewood] | 0.080 | 0.028 | 0.031 | 0.131 | 0.001 | 0.000 | 2147.0 | 2488.0 | 1.00 | 24.614628 |
| frac[mahogany] | 0.014 | 0.012 | 0.000 | 0.036 | 0.001 | 0.001 | 69.0 | 109.0 | 1.04 | 0.791062 |
| conc | 5.712 | 1.741 | 2.729 | 8.872 | 0.036 | 0.026 | 2209.0 | 2082.0 | 1.00 | 25.325437 |
这很棒,但我们可以做得更好。
对于frac[mahogany],稍微过大的\(\hat{R}\)值有点令人担忧,而且令人惊讶的是,我们的\(\mathrm{ESS} \; \mathrm{sec}^{-1}\)非常小。
Dirichlet-多项式模型 - 边缘化#
幸运的是,狄利克雷分布是多项分布的共轭先验,因此存在一个方便的、封闭形式的边缘分布,即狄利克雷-多项分布,该分布在3.11.0版本中被添加到PyMC中。
让我们利用这一点,边缘化掉显式的潜在参数,\(p_i\), 用DM替换这个节点和多项式的组合,以构建一个等效的模型。
with pm.Model(coords=coords) as model_dm_marginalized:
frac = pm.Dirichlet("frac", a=np.ones(k), dims="tree")
conc = pm.Lognormal("conc", mu=1, sigma=1)
counts = pm.DirichletMultinomial(
"counts", n=total_count, a=frac * conc, observed=observed_counts, dims=("forest", "tree")
)
pm.model_to_graphviz(model_dm_marginalized)
图示显示我们已经将原本的潜在狄利克雷和多项式节点合并成了一个单一的DM节点。
with model_dm_marginalized:
trace_dm_marginalized = pm.sample(chains=4)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [frac, conc]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 2 seconds.
它采样速度更快,并且没有任何之前的警告!
az.plot_trace(data=trace_dm_marginalized, var_names=["frac", "conc"]);
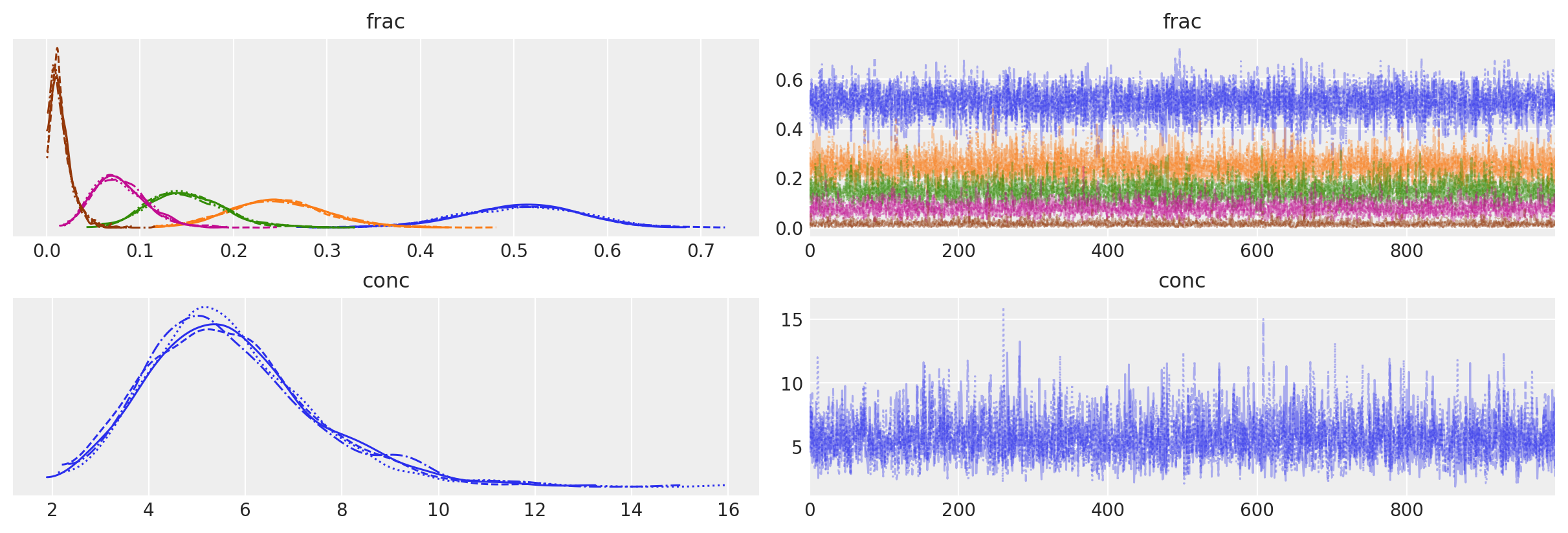
轨迹图看起来模糊,而KDE图则清晰。
summary_dm_marginalized = az.summary(trace_dm_marginalized, var_names=["frac", "conc"])
summary_dm_marginalized = summary_dm_marginalized.assign(
ess_mean_per_sec=lambda x: x.ess_bulk / trace_dm_marginalized.posterior.sampling_time,
)
assert all(summary_dm_marginalized.r_hat < 1.03)
summary_dm_marginalized
| mean | sd | hdi_3% | hdi_97% | mcse_mean | mcse_sd | ess_bulk | ess_tail | r_hat | ess_mean_per_sec | |
|---|---|---|---|---|---|---|---|---|---|---|
| frac[pine] | 0.507 | 0.063 | 0.385 | 0.619 | 0.001 | 0.001 | 4330.0 | 2816.0 | 1.0 | 1870.135862 |
| frac[oak] | 0.248 | 0.051 | 0.150 | 0.341 | 0.001 | 0.000 | 6017.0 | 3571.0 | 1.0 | 2598.754615 |
| frac[ebony] | 0.150 | 0.040 | 0.080 | 0.226 | 0.001 | 0.000 | 4315.0 | 3296.0 | 1.0 | 1863.657331 |
| frac[rosewood] | 0.079 | 0.028 | 0.031 | 0.130 | 0.000 | 0.000 | 3027.0 | 2718.0 | 1.0 | 1307.367495 |
| frac[mahogany] | 0.016 | 0.011 | 0.001 | 0.036 | 0.000 | 0.000 | 2856.0 | 2172.0 | 1.0 | 1233.512245 |
| conc | 5.692 | 1.719 | 2.807 | 9.045 | 0.028 | 0.020 | 3594.0 | 2925.0 | 1.0 | 1552.255956 |
我们看到 \(\hat{R}\) 在各处都接近 \(1\), 并且 \(\mathrm{ESS} \; \mathrm{sec}^{-1}\) 要高得多。 我们的重新参数化(边缘化)极大地改善了采样! (而且,谢天谢地,HDI看起来与其他模型相似。)
这一切看起来都非常好,但如果我们没有真实标签呢?
后验预测检查来救援(再次)!
with model_dm_marginalized:
pp_samples = pm.sample_posterior_predictive(trace_dm_marginalized)
# Concatenate with InferenceData object
trace_dm_marginalized.extend(pp_samples)
Sampling: [counts]
cmap = plt.get_cmap("tab10")
fig, axs = plt.subplots(k, 2, sharex=True, sharey=True, figsize=(8, 8))
for j, row in enumerate(axs):
c = cmap(j)
for _trace, ax in zip([trace_dm_marginalized, trace_multinomial], row):
ax.hist(
_trace.posterior_predictive.counts.sel(tree=trees[j]).values.flatten(),
bins=np.arange(total_count),
histtype="step",
color=c,
density=True,
label="Post.Pred.",
)
ax.hist(
(_trace.observed_data.counts.sel(tree=trees[j]).values.flatten()),
bins=np.arange(total_count),
color=c,
density=True,
alpha=0.25,
label="Observed",
)
ax.axvline(
true_frac[j] * total_count,
color=c,
lw=1.0,
alpha=0.45,
label="True",
)
row[1].annotate(
f"{trees[j]}",
xy=(0.96, 0.9),
xycoords="axes fraction",
ha="right",
va="top",
color=c,
)
axs[-1, -1].legend(loc="upper center", fontsize=10)
axs[0, 1].set_title("Multinomial")
axs[0, 0].set_title("Dirichlet-multinomial")
axs[-1, 0].set_xlabel("Count")
axs[-1, 1].set_xlabel("Count")
axs[-1, 0].set_yticks([0, 0.5, 1.0])
axs[-1, 0].set_ylim(0, 0.6)
ax.set_ylim(0, 0.6);
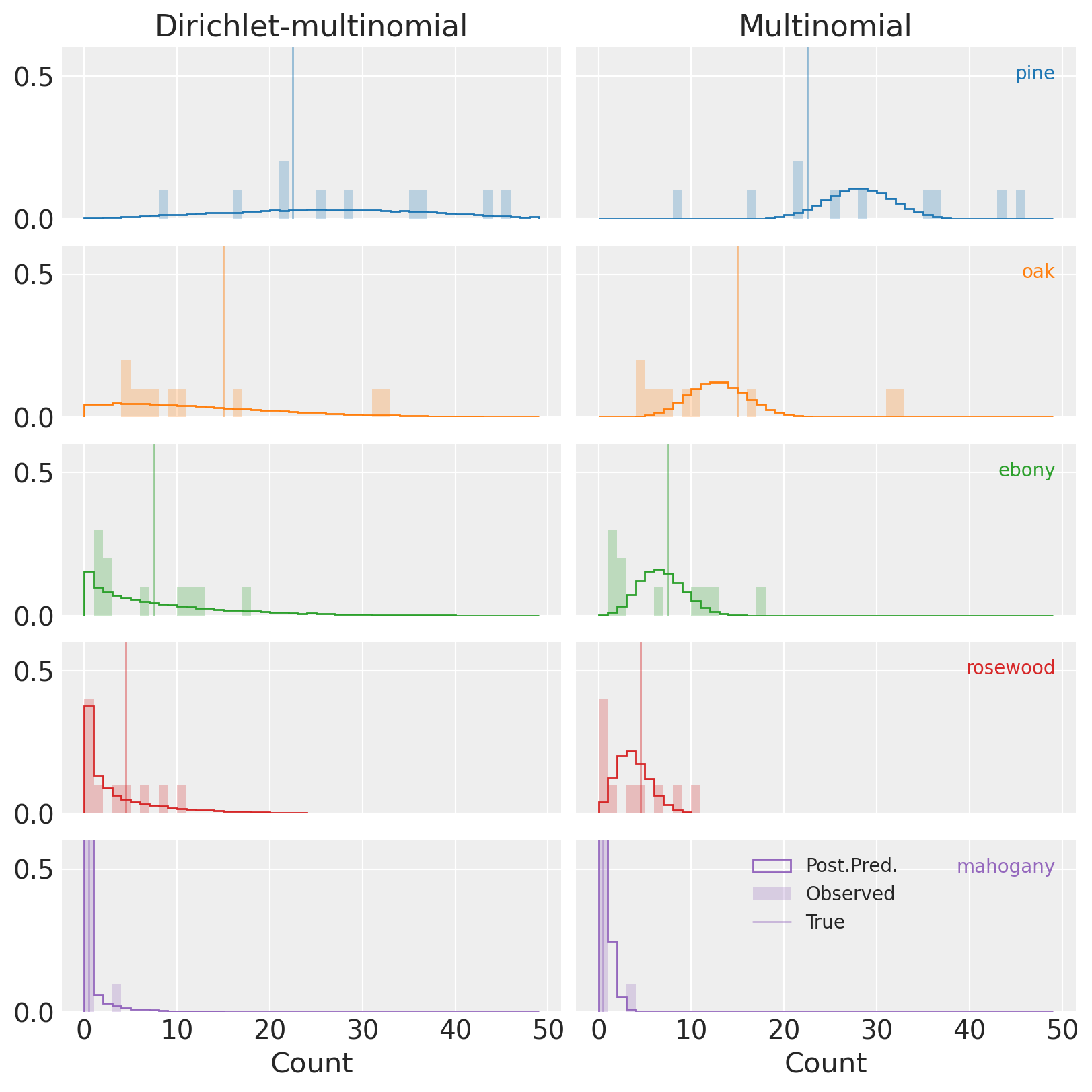
(再次注意,y轴没有完全显示高度,并且剪切了紫色中的红木分布。)
与多项式(右侧图表)相比,DM(左侧)的PPCs显示观测数据是我们模型的完全合理的实现。 这是个好消息!
模型比较#
让我们更进一步,尝试量化我们的DM模型相对于原始多项式模型的改进程度。 我们将使用留一交叉验证来比较两者的样本外预测能力。
with model_multinomial:
pm.compute_log_likelihood(trace_multinomial)
with model_dm_marginalized:
pm.compute_log_likelihood(trace_dm_marginalized)
az.compare(
{"multinomial": trace_multinomial, "dirichlet_multinomial": trace_dm_marginalized}, ic="loo"
)
/home/erik/mambaforge/envs/pymc_examples/lib/python3.11/site-packages/arviz/stats/stats.py:803: UserWarning: Estimated shape parameter of Pareto distribution is greater than 0.7 for one or more samples. You should consider using a more robust model, this is because importance sampling is less likely to work well if the marginal posterior and LOO posterior are very different. This is more likely to happen with a non-robust model and highly influential observations.
warnings.warn(
/home/erik/mambaforge/envs/pymc_examples/lib/python3.11/site-packages/arviz/stats/stats.py:307: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value 'False' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
df_comp.loc[val] = (
/home/erik/mambaforge/envs/pymc_examples/lib/python3.11/site-packages/arviz/stats/stats.py:307: FutureWarning: Setting an item of incompatible dtype is deprecated and will raise in a future error of pandas. Value 'log' has dtype incompatible with float64, please explicitly cast to a compatible dtype first.
df_comp.loc[val] = (
| rank | elpd_loo | p_loo | elpd_diff | weight | se | dse | warning | scale | |
|---|---|---|---|---|---|---|---|---|---|
| dirichlet_multinomial | 0 | -96.773440 | 4.126392 | 0.000000 | 1.000000e+00 | 6.823526 | 0.000000 | False | log |
| multinomial | 1 | -174.447424 | 24.065196 | 77.673984 | 2.735590e-13 | 24.884526 | 23.983963 | True | log |
不出所料,DM模型远远优于多项分布模型,将100%的权重分配给了过度分散的模型。
虽然多项分布的warning=True标志表明数值结果不能完全信任,但elpd_loo的巨大差异进一步证实了在这两者之间,DM模型在预测、参数推断等方面应得到极大的青睐。
结论#
显然,在每种情况下,DM 模型并不是一个完美的模型,但它通常比多项式模型更优,同时在仅增加一个额外参数的情况下更加稳健。
在选择模型时,我们应该记住DM存在一些不足之处。最大的问题是,尽管DM比多项式模型更灵活,但它仍然忽略了类别之间潜在的相关性。例如,如果我们的某一种树种依赖于另一种树种,那么我们在这里使用的模型将无法有效地考虑到这一点。在这种情况下,将普通的Dirichlet分布替换为更复杂的形式(例如广义Dirichlet分布或Logistic-多元正态分布)可能是值得考虑的。
参考资料#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,xarray
Last updated: Thu Oct 05 2023
Python implementation: CPython
Python version : 3.11.6
IPython version : 8.16.1
pytensor: 2.17.1
xarray : 2023.9.0
numpy : 1.25.2
arviz : 0.16.1
scipy : 1.11.3
pymc : 5.9.0
matplotlib: 3.8.0
Watermark: 2.4.3