用于密度估计的Dirichlet过程混合模型#
狄利克雷过程#
Dirichlet 过程是一个在分布空间上的灵活概率分布。最一般地,一个概率分布 \(P\) 在集合 \(\Omega\) 上是一个[测度](https://en.wikipedia.org/wiki/Measure_(mathematics%29),它将整个空间的测度赋值为1(\(P(\Omega) = 1\))。Dirichlet 过程 \(P \sim \textrm{DP}(\alpha, P_0)\) 是一个具有以下性质的测度:对于每一个有限的不相交划分 \(S_1, \ldots, S_n\) 的 \(\Omega\),
这里 \(P_0\) 是空间 \(\Omega\) 上的基础概率测度。精度参数 \(\alpha > 0\) 控制从Dirichlet过程采样的样本与基础测度 \(P_0\) 的接近程度。当 \(\alpha \to \infty\) 时,从Dirichlet过程采样的样本趋近于基础测度 \(P_0\)。
狄利克雷过程具有几个特性,使它们非常适合用于MCMC模拟。
给定来自狄利克雷过程\(P \sim \textrm{DP}(\alpha, P_0)\)的独立同分布i.i.d.观测\(\omega_1, \ldots, \omega_n\),其后验也是一个狄利克雷过程,并且
\[P\ |\ \omega_1, \ldots, \omega_n \sim \textrm{DP}\left(\alpha + n, \frac{\alpha}{\alpha + n} P_0 + \frac{1}{\alpha + n} \sum_{i = 1}^n \delta_{\omega_i}\right),\]
其中 \(\delta\) 是 狄拉克δ函数
新观测值的后验预测分布是基础测度和观测值之间的折衷,
\[\omega\ |\ \omega_1, \ldots, \omega_n \sim \frac{\alpha}{\alpha + n} P_0 + \frac{1}{\alpha + n} \sum_{i = 1}^n \delta_{\omega_i}.\]
我们看到先验精度 \(\alpha\) 可以自然地解释为先验样本大小。 这种后验预测分布的形式也适合于吉布斯采样。
样本, \(P \sim \textrm{DP}(\alpha, P_0)\), 来自Dirichlet过程的是离散的,概率为1。也就是说,存在元素 \(\omega_1, \omega_2, \ldots\) 在 \(\Omega\) 中,并且权重 \(\mu_1, \mu_2, \ldots\) 满足 \(\sum_{i = 1}^{\infty} \mu_i = 1\),使得
\[P = \sum_{i = 1}^\infty \mu_i \delta_{\omega_i}.\]The stick-breaking process 提供了权重 \(\mu_i\) 和样本 \(\omega_i\) 的显式构造,这些构造可以直接从中采样。如果 \(\beta_1, \beta_2, \ldots \sim \textrm{Beta}(1, \alpha)\),那么 \(\mu_i = \beta_i \prod_{j = 1}^{i - 1} (1 - \beta_j)\)。这种表示与棍子折断之间的关系可以如下所示:
从长度为一的棍子开始。
将棍子分成两部分,第一部分的比例为 \(\mu_1 = \beta_1\),第二部分的比例为 \(1 - \mu_1\)。
进一步将第二部分分成两部分,第一部分的比率为 \(\beta_2\),第二部分的比率为 \(1 - \beta_2\)。 这部分的第一部分的长度为 \(\beta_2 (1 - \beta_1)\); 第二部分的长度为 \((1 - \beta_1) (1 - \beta_2)\)。
继续以这种方式从上一次中断处拆分第二部分,永远如此。如果 \(\omega_1, \omega_2, \ldots \sim P_0\),那么
\[P = \sum_{i = 1}^\infty \mu_i \delta_{\omega_i} \sim \textrm{DP}(\alpha, P_0).\]
[建议进一步阅读]: (http://mlg.eng.cam.ac.uk/tutorials/07/ywt.pdf) 和 以简要介绍其他类型的狄利克雷过程及其应用。
我们可以使用上述的stick-breaking过程在Python中轻松地从一个Dirichlet过程中进行采样。在这个例子中,\(\alpha = 2\),基础分布是\(N(0, 1)\)。
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
import pytensor.tensor as pt
import scipy as sp
import seaborn as sns
import xarray as xr
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
N = 20
K = 30
alpha = 2.0
P0 = sp.stats.norm
我们从stick-breaking过程中抽取并绘制样本。
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
omega = P0.rvs(size=(N, K))
x_plot = xr.DataArray(np.linspace(-3, 3, 200), dims=["plot"])
sample_cdfs = (w[..., np.newaxis] * np.less.outer(omega, x_plot.values)).sum(axis=1)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x_plot, sample_cdfs[0], c="gray", alpha=0.75, label="DP sample CDFs")
ax.plot(x_plot, sample_cdfs[1:].T, c="gray", alpha=0.75)
ax.plot(x_plot, P0.cdf(x_plot), c="k", label="Base CDF")
ax.set_title(rf"$\alpha = {alpha}$")
ax.legend(loc=2);
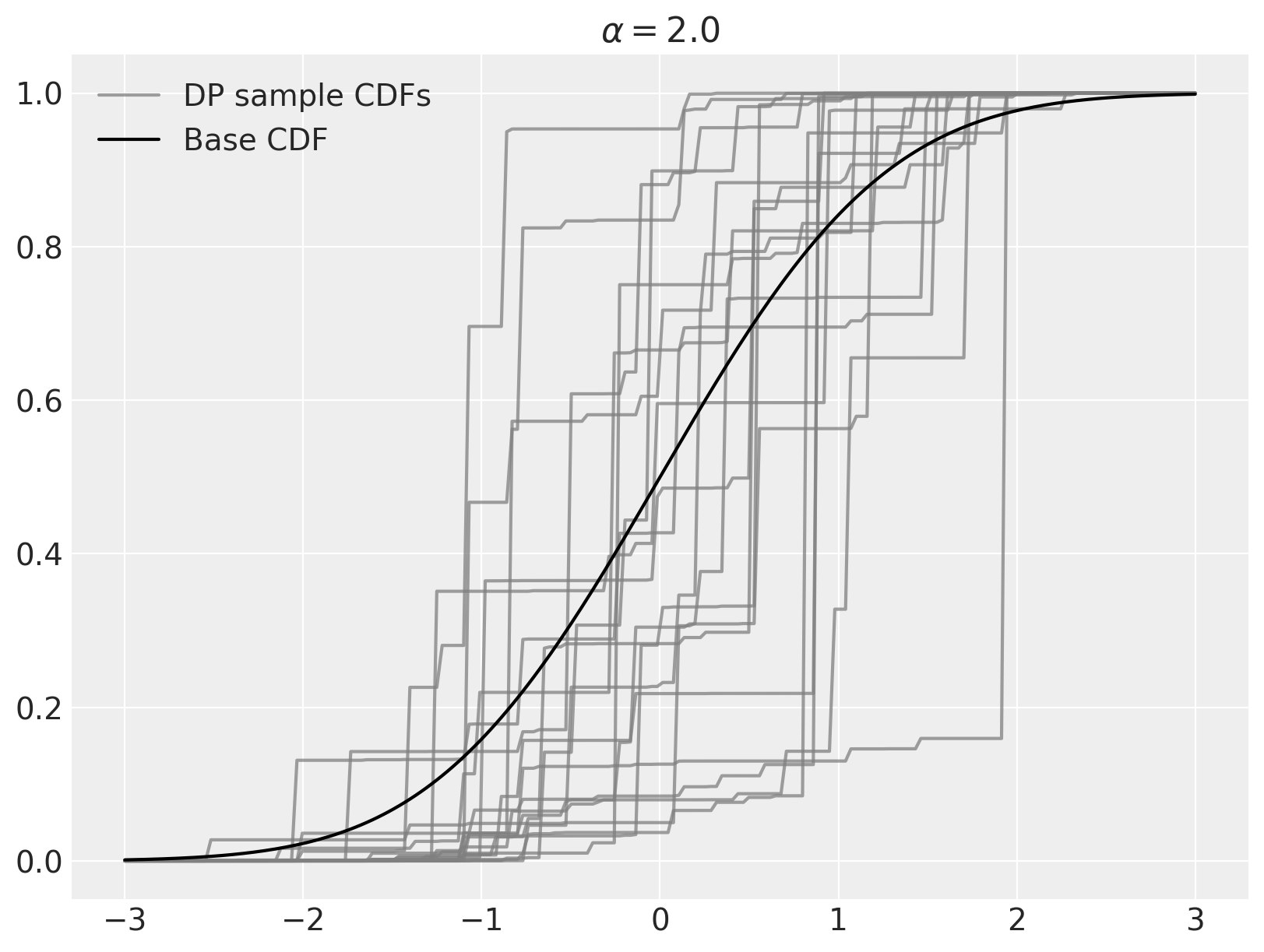
如上所述,当 \(\alpha \to \infty\) 时,从狄利克雷过程得到的样本会收敛到基础分布。
fig, (l_ax, r_ax) = plt.subplots(ncols=2, sharex=True, sharey=True, figsize=(16, 6))
K = 50
alpha = 10.0
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
omega = P0.rvs(size=(N, K))
sample_cdfs = (w[..., np.newaxis] * np.less.outer(omega, x_plot.values)).sum(axis=1)
l_ax.plot(x_plot, sample_cdfs[0], c="gray", alpha=0.75, label="DP sample CDFs")
l_ax.plot(x_plot, sample_cdfs[1:].T, c="gray", alpha=0.75)
l_ax.plot(x_plot, P0.cdf(x_plot), c="k", label="Base CDF")
l_ax.set_title(rf"$\alpha = {alpha}$")
l_ax.legend(loc=2)
K = 200
alpha = 50.0
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
omega = P0.rvs(size=(N, K))
sample_cdfs = (w[..., np.newaxis] * np.less.outer(omega, x_plot.values)).sum(axis=1)
r_ax.plot(x_plot, sample_cdfs[0], c="gray", alpha=0.75, label="DP sample CDFs")
r_ax.plot(x_plot, sample_cdfs[1:].T, c="gray", alpha=0.75)
r_ax.plot(x_plot, P0.cdf(x_plot), c="k", label="Base CDF")
r_ax.set_title(rf"$\alpha = {alpha}$")
r_ax.legend(loc=2);
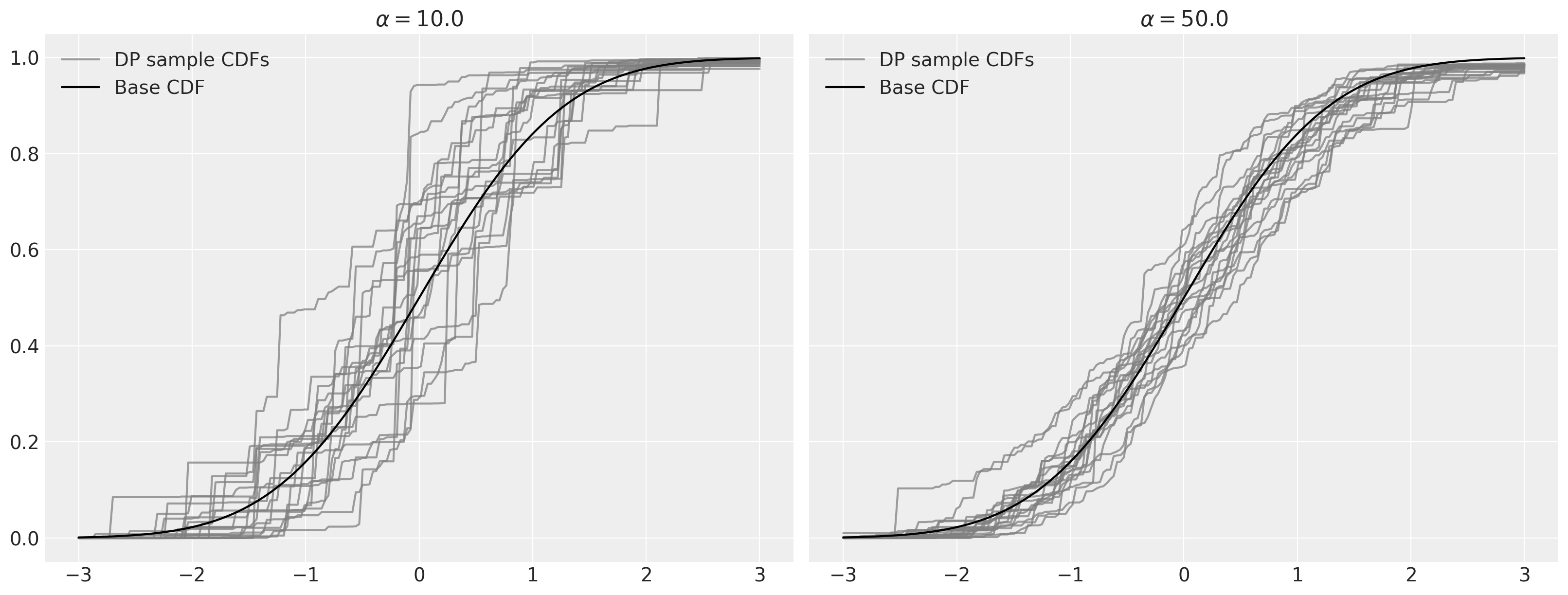
狄利克雷过程混合模型#
对于密度估计任务,Dirichlet 过程样本的(几乎确定的)离散性是一个显著的缺点。 这个问题可以通过使用 Dirichlet 过程混合来进行密度估计来解决,增加了一层间接性。 Dirichlet 过程混合使用来自参数族的组件密度 \(\mathcal{F} = \{f_{\theta}\ |\ \theta \in \Theta\}\) 并将混合权重表示为 Dirichlet 过程。 如果 \(P_0\) 是参数空间 \(\Theta\) 上的概率测度,则 Dirichlet 过程混合是层次模型
为了说明这个模型,我们模拟从一个Dirichlet过程混合模型中抽取样本,其中\(\alpha = 2\),\(\theta \sim N(0, 1)\),\(x\ |\ \theta \sim N(\theta, (0.3)^2)\)。
N = 5
K = 30
alpha = 2
P0 = sp.stats.norm
f = lambda x, theta: sp.stats.norm.pdf(x, theta, 0.3)
beta = sp.stats.beta.rvs(1, alpha, size=(N, K))
w = np.empty_like(beta)
w[:, 0] = beta[:, 0]
w[:, 1:] = beta[:, 1:] * (1 - beta[:, :-1]).cumprod(axis=1)
theta = P0.rvs(size=(N, K))
dpm_pdf_components = f(x_plot, theta[..., np.newaxis])
dpm_pdfs = (w[..., np.newaxis] * dpm_pdf_components).sum(axis=1)
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x_plot, dpm_pdfs.T, c="gray")
ax.set_yticklabels([]);
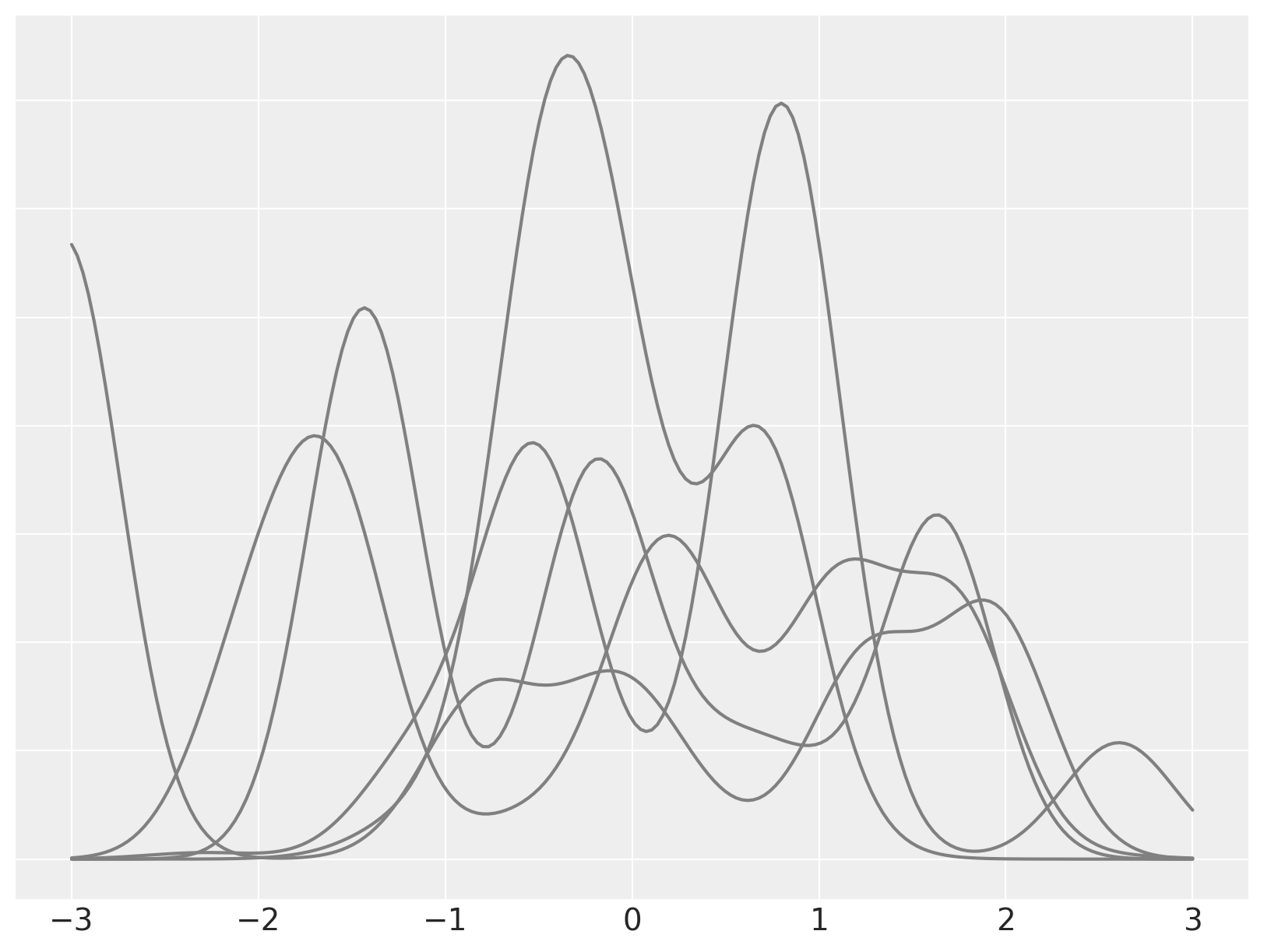
我们现在专注于单一的混合物,并将其分解为其各个(加权的)混合成分。
fig, ax = plt.subplots(figsize=(8, 6))
ix = 1
ax.plot(x_plot, dpm_pdfs[ix], c="k", label="Density")
ax.plot(
x_plot,
(w[..., np.newaxis] * dpm_pdf_components)[ix, 0],
"--",
c="k",
label="Mixture components (weighted)",
)
ax.plot(x_plot, (w[..., np.newaxis] * dpm_pdf_components)[ix].T, "--", c="k")
ax.set_yticklabels([])
ax.legend(loc=1);
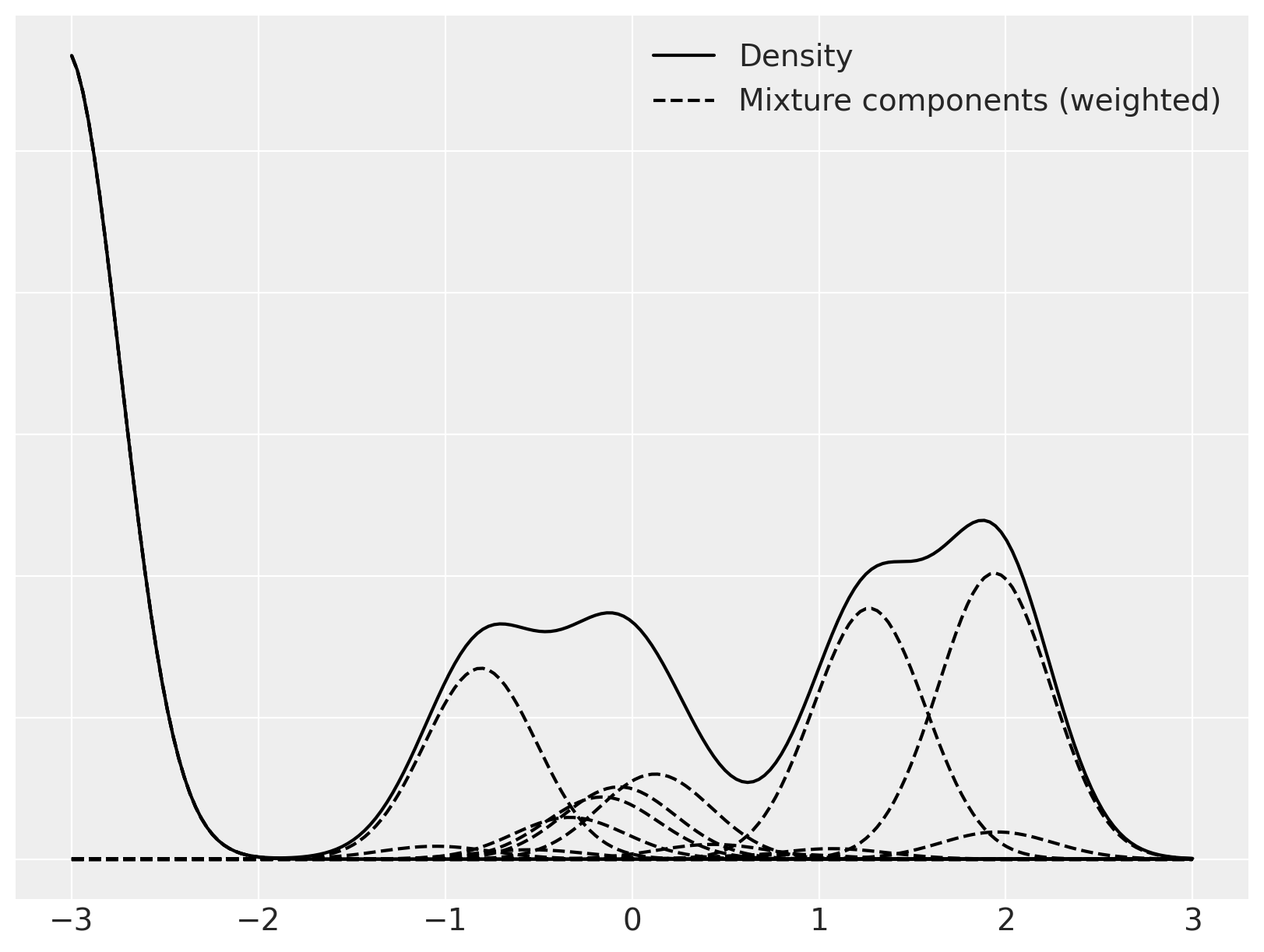
从这些随机过程中进行采样很有趣,但当我们将其拟合到数据时,这些想法才真正变得有用。样本的离散性和狄利克雷过程的破碎表示使其非常适合于后验分布的马尔可夫链蒙特卡罗模拟。我们将使用PyMC进行此采样。
我们的第一个示例使用Dirichlet过程混合来估计老忠实间歇泉在黄石国家公园中喷发之间的等待时间的密度。
try:
old_faithful_df = pd.read_csv(os.path.join("..", "data", "old_faithful.csv"))
except FileNotFoundError:
old_faithful_df = pd.read_csv(pm.get_data("old_faithful.csv"))
为了方便指定先验,我们对喷发之间的等待时间进行了标准化。
old_faithful_df["std_waiting"] = (
old_faithful_df.waiting - old_faithful_df.waiting.mean()
) / old_faithful_df.waiting.std()
old_faithful_df.head()
| eruptions | waiting | std_waiting | |
|---|---|---|---|
| 0 | 3.600 | 79 | 0.596025 |
| 1 | 1.800 | 54 | -1.242890 |
| 2 | 3.333 | 74 | 0.228242 |
| 3 | 2.283 | 62 | -0.654437 |
| 4 | 4.533 | 85 | 1.037364 |
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 20
ax.hist(old_faithful_df.std_waiting, bins=n_bins, color="C0", lw=0, alpha=0.5)
ax.set_xlabel("Standardized waiting time between eruptions")
ax.set_ylabel("Number of eruptions");
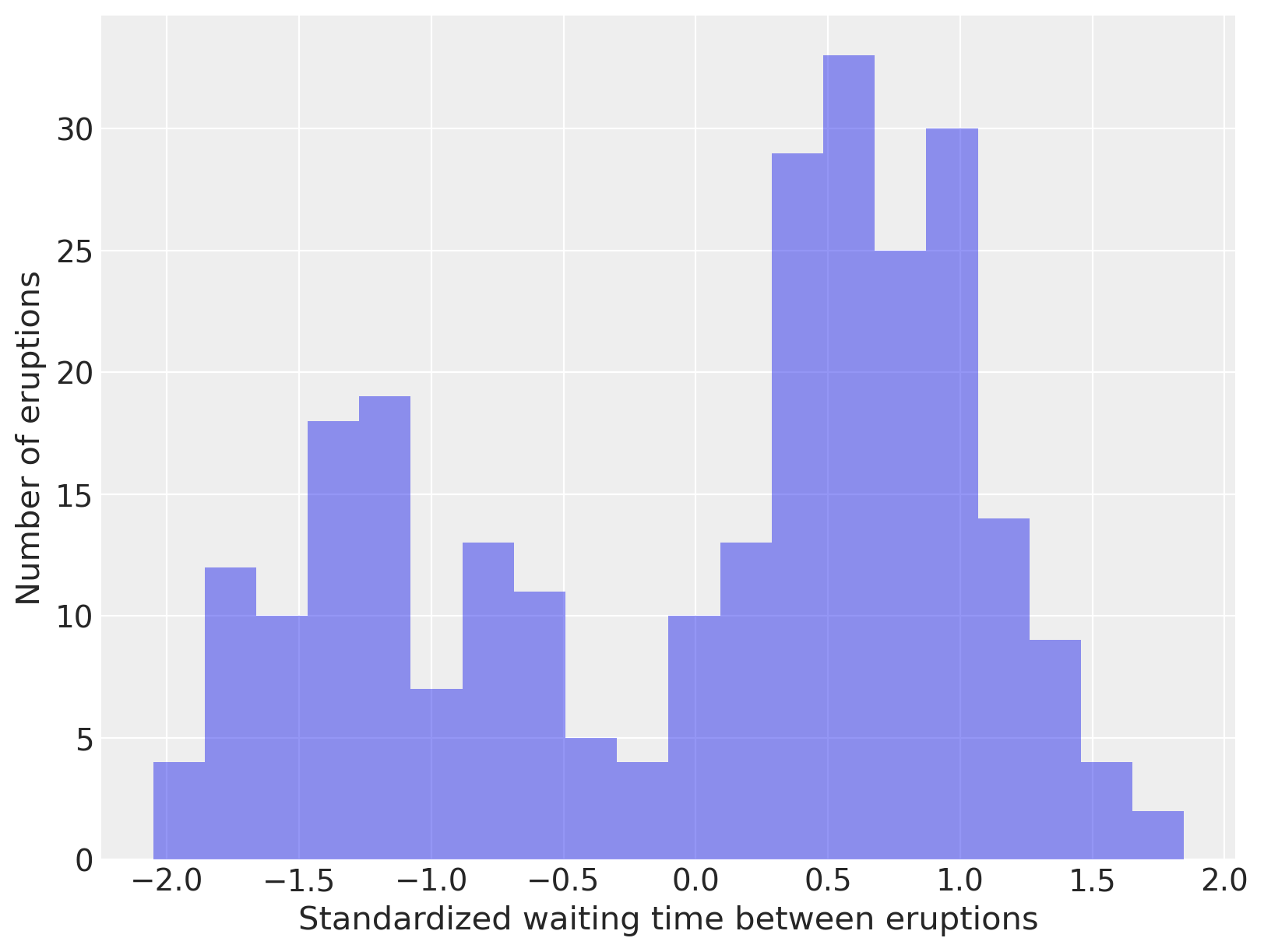
细心的读者会注意到,我们并没有按照其定义所指示的那样无限期地继续stick-breaking过程,而是在有限次数的断裂后截断了这一过程。显然,在计算Dirichlet过程时,只需要在内存中存储有限数量的点质量和权重。这一限制并不十分繁重,因为对于有限数量的观测值,混合成分的数量似乎不太可能比样本数量增长得更快。这种直觉可以形式化地表明,对混合贡献非可忽略质量的成分数量(期望)趋近于\(\alpha \log N\),其中\(N\)是样本大小。
有各种巧妙的吉布斯采样技术用于狄利克雷过程,这些技术允许存储的组件数量根据需要增长。随机记忆化[]是另一种强大的技术,用于模拟狄利克雷过程,同时仅在内存中存储有限数量的组件。在这个入门示例中,我们采用了简单得多的方法,即在固定数量的组件\(K\)之后截断存储的狄利克雷过程组件。和为截断提供了依据,表明\(K > 5 \alpha + 2\)很可能足以捕捉几乎所有的混合权重(\(\sum_{i = 1}^{K} w_i > 0.99\))。在实践中,我们可以通过检查对混合贡献非可忽略质量的组件数量来验证我们对狄利克雷过程的截断近似的适用性。如果在我们的模拟中,所有组件都对混合贡献了非可忽略的质量,那么我们可能过早地截断了狄利克雷过程。
我们的(截断的)标准化等待时间的Dirichlet过程混合模型是
请注意,与之前的模拟不同,我们没有固定\(\alpha\)的值,而是指定了一个先验分布,这样我们就可以从观测数据中学习其后验分布。
我们现在使用PyMC构建这个模型。
N = old_faithful_df.shape[0]
K = 30
def stick_breaking(beta):
portion_remaining = pt.concatenate([[1], pt.extra_ops.cumprod(1 - beta)[:-1]])
return beta * portion_remaining
with pm.Model(coords={"component": np.arange(K), "obs_id": np.arange(N)}) as model:
alpha = pm.Gamma("alpha", 1.0, 1.0)
beta = pm.Beta("beta", 1.0, alpha, dims="component")
w = pm.Deterministic("w", stick_breaking(beta), dims="component")
tau = pm.Gamma("tau", 1.0, 1.0, dims="component")
lambda_ = pm.Gamma("lambda_", 10.0, 1.0, dims="component")
mu = pm.Normal("mu", 0, tau=lambda_ * tau, dims="component")
obs = pm.NormalMixture(
"obs", w, mu, tau=lambda_ * tau, observed=old_faithful_df.std_waiting.values, dims="obs_id"
)
我们使用NUTS从模型中采样1,000次,初始化为ADVI。
with model:
trace = pm.sample(
tune=2500,
init="advi",
target_accept=0.975,
random_seed=RANDOM_SEED,
)
Sampling 4 chains for 2_500 tune and 1_000 draw iterations (10_000 + 4_000 draws total) took 127 seconds.
后验分布在 \(\alpha\) 之间高度集中在 0.25 和 1 之间。
az.plot_trace(trace, var_names=["alpha"]);

为了验证截断不会使我们的结果产生偏差,我们绘制了每个成分的后验期望混合权重。
fig, ax = plt.subplots(figsize=(8, 6))
plot_w = np.arange(K) + 1
ax.bar(plot_w - 0.5, trace.posterior["w"].mean(("chain", "draw")), width=1.0, lw=0)
ax.set_xlim(0.5, K)
ax.set_xlabel("Component")
ax.set_ylabel("Posterior expected mixture weight");
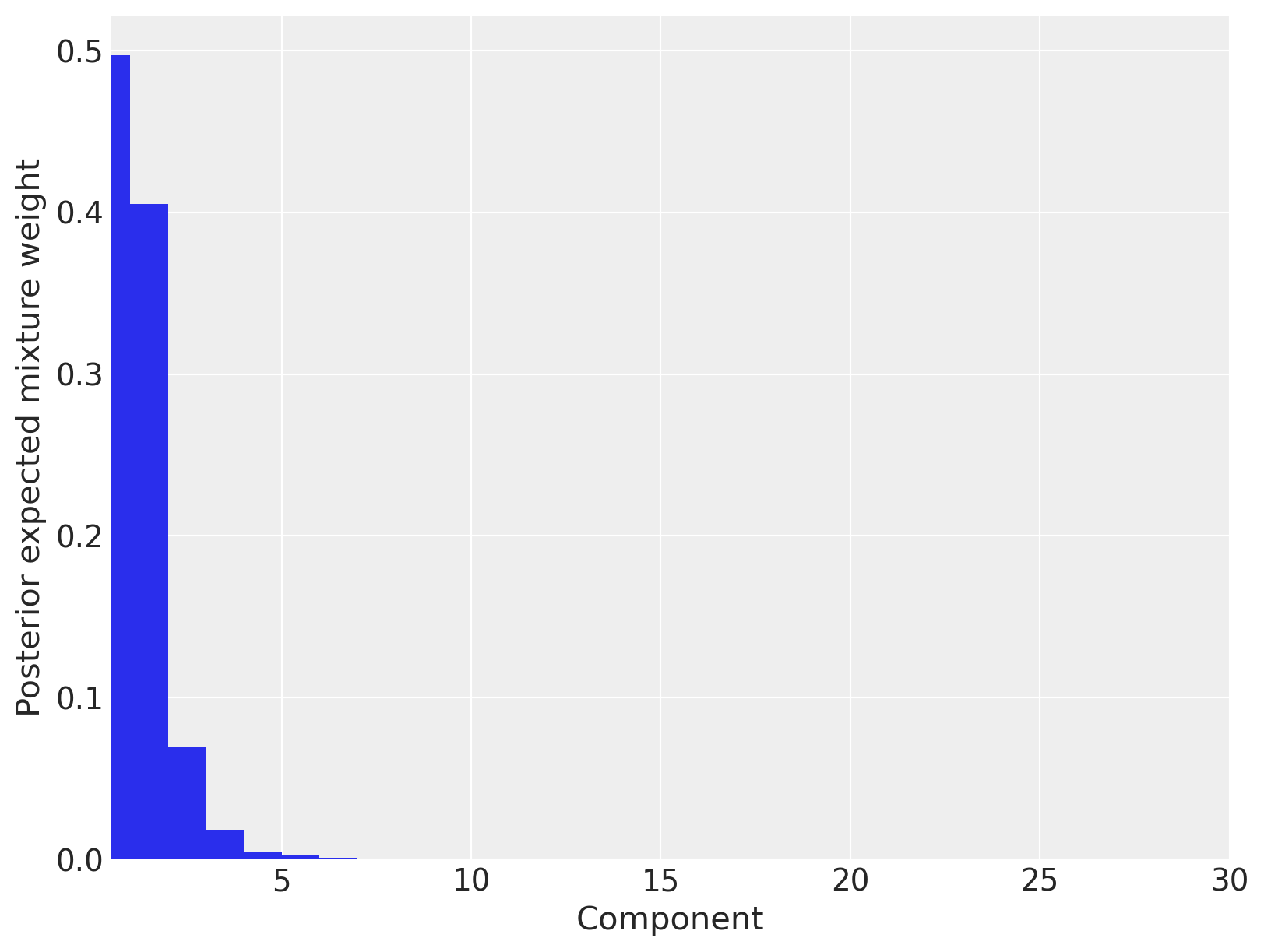
我们看到只有三个混合成分具有可观的后期望权重,因此我们得出结论,将Dirichlet过程截断为三十个成分并没有显著影响我们的估计。
我们现在计算并绘制我们的后验密度估计。
post_pdf_contribs = xr.apply_ufunc(
sp.stats.norm.pdf,
x_plot,
trace.posterior["mu"],
1.0 / np.sqrt(trace.posterior["lambda_"] * trace.posterior["tau"]),
)
post_pdfs = (trace.posterior["w"] * post_pdf_contribs).sum(dim=("component"))
post_pdf_quantiles = post_pdfs.quantile([0.1, 0.9], dim=("chain", "draw"))
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 20
ax.hist(old_faithful_df.std_waiting.values, bins=n_bins, density=True, color="C0", lw=0, alpha=0.5)
ax.fill_between(
x_plot,
post_pdf_quantiles.sel(quantile=0.1),
post_pdf_quantiles.sel(quantile=0.9),
color="gray",
alpha=0.45,
)
ax.plot(x_plot, post_pdfs.sel(chain=0, draw=0), c="gray", label="Posterior sample densities")
ax.plot(
x_plot,
az.extract(post_pdfs, var_names="x", num_samples=100),
c="gray",
)
ax.plot(x_plot, post_pdfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.set_xlabel("Standardized waiting time between eruptions")
ax.set_yticklabels([])
ax.set_ylabel("Density")
ax.legend(loc=2);
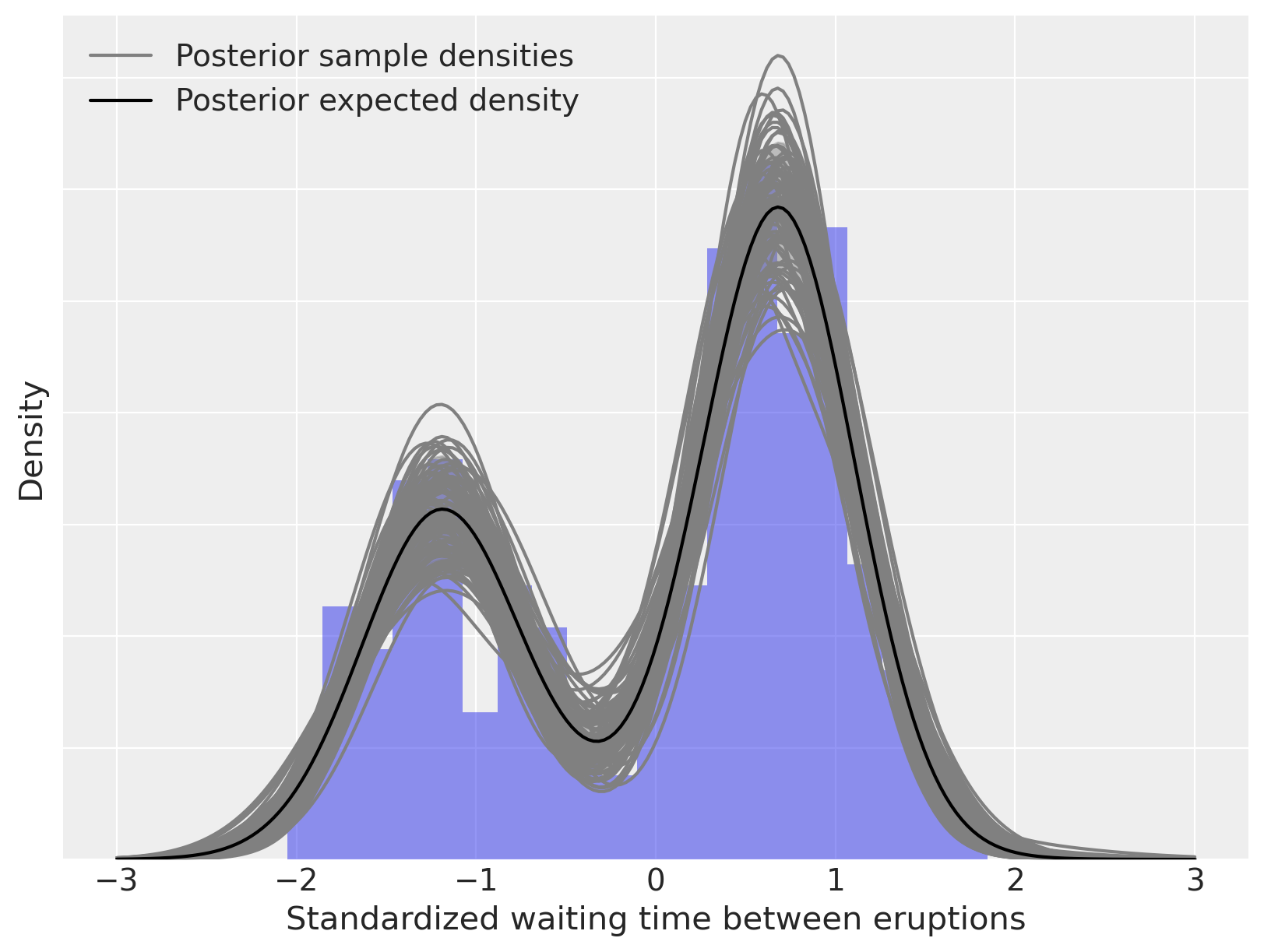
如上所述,我们可以将这个密度估计分解为其(加权的)混合成分。
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 20
ax.hist(old_faithful_df.std_waiting.values, bins=n_bins, density=True, color="C0", lw=0, alpha=0.5)
ax.plot(x_plot, post_pdfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.plot(
x_plot,
(trace.posterior["w"] * post_pdf_contribs).mean(dim=("chain", "draw")).sel(component=0),
"--",
c="k",
label="Posterior expected mixture\ncomponents\n(weighted)",
)
ax.plot(
x_plot,
(trace.posterior["w"] * post_pdf_contribs).mean(dim=("chain", "draw")).T,
"--",
c="k",
)
ax.set_xlabel("Standardized waiting time between eruptions")
ax.set_yticklabels([])
ax.set_ylabel("Density")
ax.legend(loc=2);
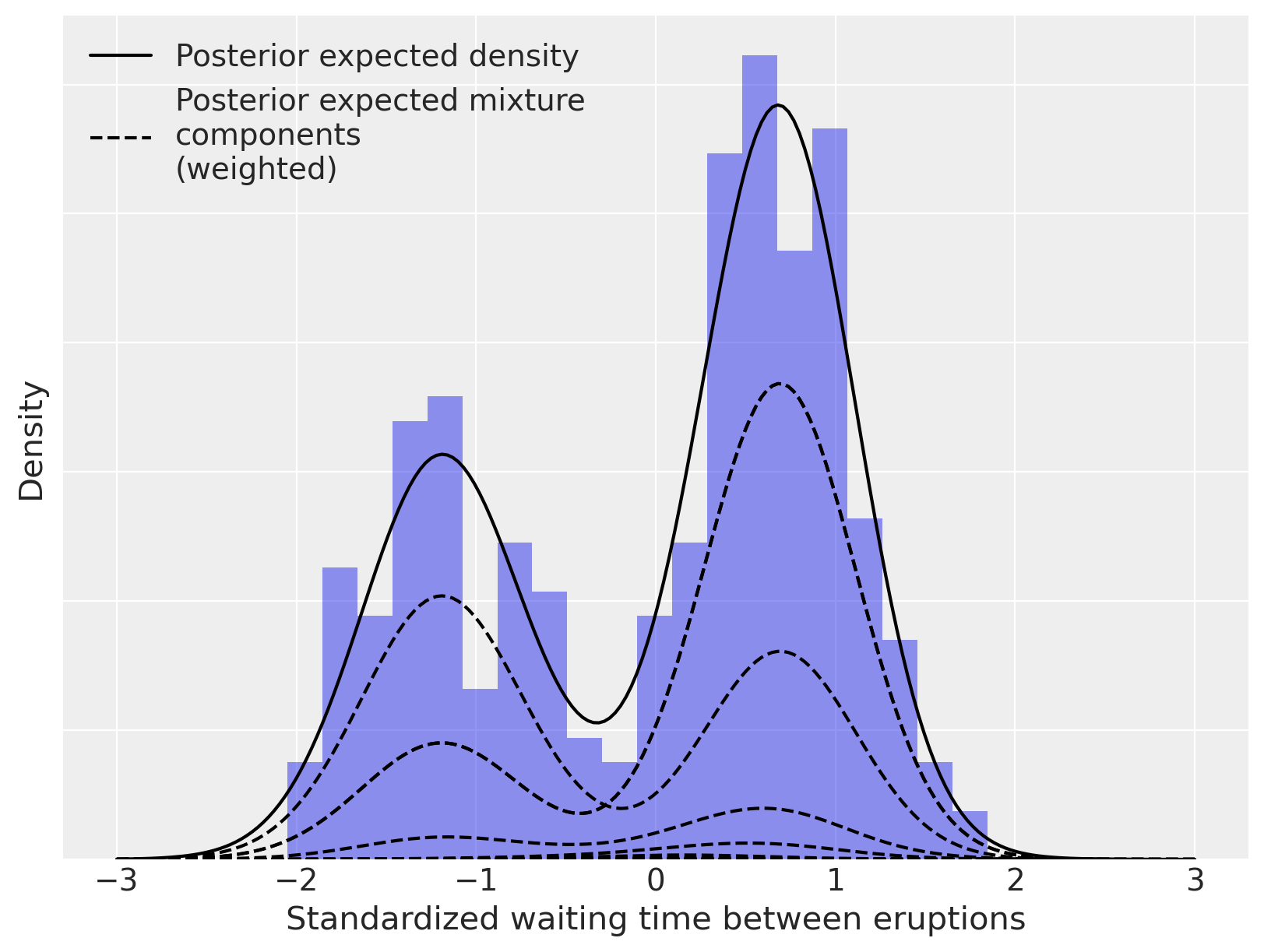
Dirichlet 过程混合模型在参数化成分分布族方面非常灵活 \(\{f_{\theta}\ |\ f_{\theta} \in \Theta\}\)。 我们在下面通过使用泊松成分分布来估计每年太阳黑子的密度来展示这种灵活性。该数据集由 整理,可以下载。
kwargs = dict(sep=";", names=["time", "sunspot.year"], usecols=[0, 1])
try:
sunspot_df = pd.read_csv(os.path.join("..", "data", "sunspot.csv"), **kwargs)
except FileNotFoundError:
sunspot_df = pd.read_csv(pm.get_data("sunspot.csv"), **kwargs)
sunspot_df.head()
| time | sunspot.year | |
|---|---|---|
| 0 | 1700.5 | 8.3 |
| 1 | 1701.5 | 18.3 |
| 2 | 1702.5 | 26.7 |
| 3 | 1703.5 | 38.3 |
| 4 | 1704.5 | 60.0 |
对于此示例,模型是
K = 50
N = sunspot_df.shape[0]
with pm.Model(coords={"component": np.arange(K), "obs_id": np.arange(N)}) as model:
alpha = pm.Gamma("alpha", 1.0, 1.0)
beta = pm.Beta("beta", 1, alpha, dims="component")
w = pm.Deterministic("w", stick_breaking(beta), dims="component")
# Gamma is conjugate prior to Poisson
lambda_ = pm.Gamma("lambda_", 300.0, 2.0, dims="component")
obs = pm.Mixture(
"obs", w, pm.Poisson.dist(lambda_), observed=sunspot_df["sunspot.year"], dims="obs_id"
)
with model:
trace = pm.sample(
tune=5000,
init="advi",
target_accept=0.95,
random_seed=RANDOM_SEED,
)
Sampling 4 chains for 5_000 tune and 1_000 draw iterations (20_000 + 4_000 draws total) took 508 seconds.
对于太阳黑子模型,\(\alpha\) 的后验分布集中在 0.6 到 1.2 之间,表明与老忠实间歇泉等待时间模型相比,我们应该预期有更多的成分对混合模型贡献不可忽略的量。
az.plot_trace(trace, var_names=["alpha"]);

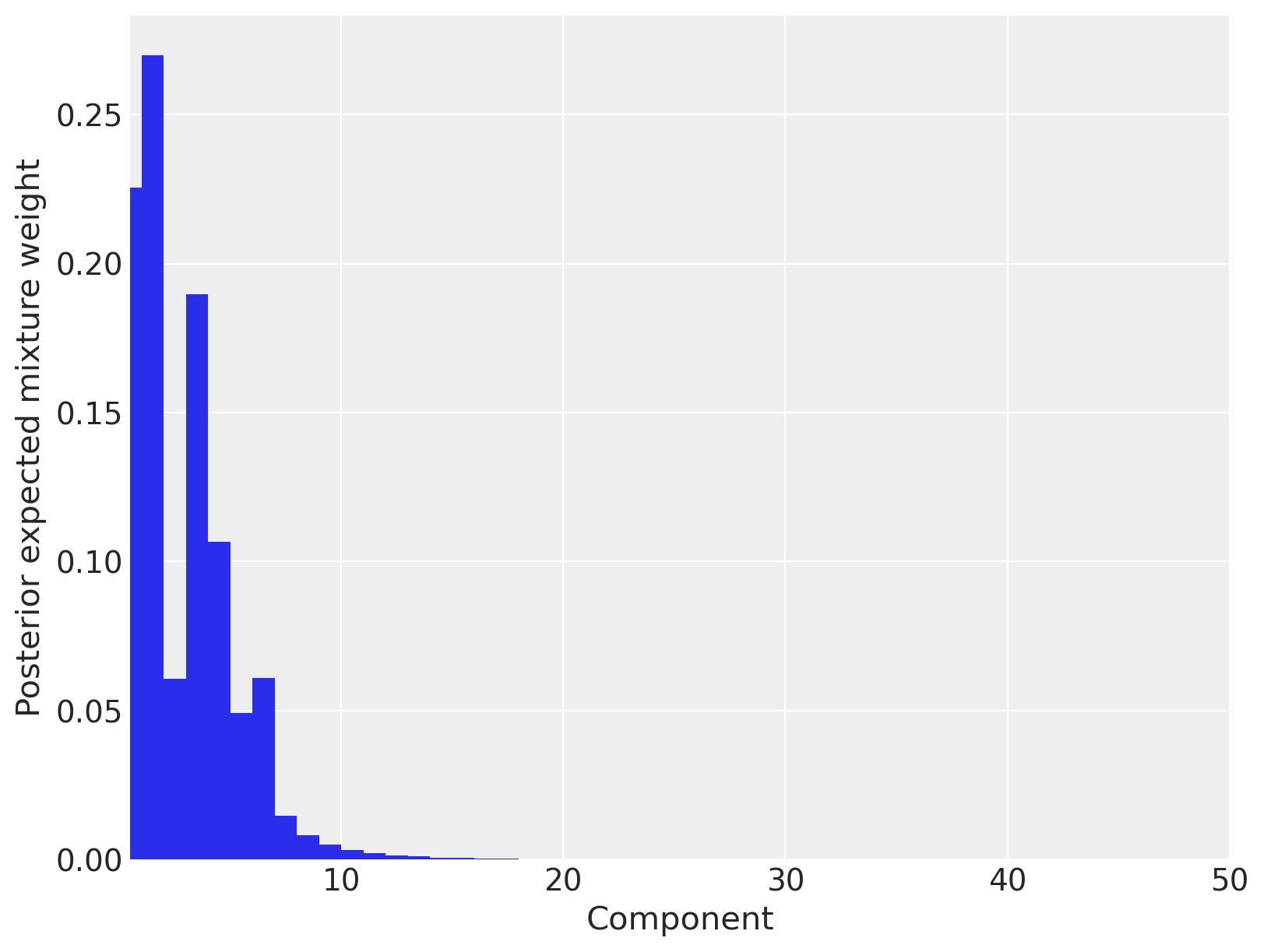
事实上,我们看到在十个到十五个混合成分之间具有可观的后验期望权重。
fig, ax = plt.subplots(figsize=(8, 6))
plot_w = np.arange(K) + 1
ax.bar(plot_w - 0.5, trace.posterior["w"].mean(("chain", "draw")), width=1.0, lw=0)
ax.set_xlim(0.5, K)
ax.set_xlabel("Component")
ax.set_ylabel("Posterior expected mixture weight");
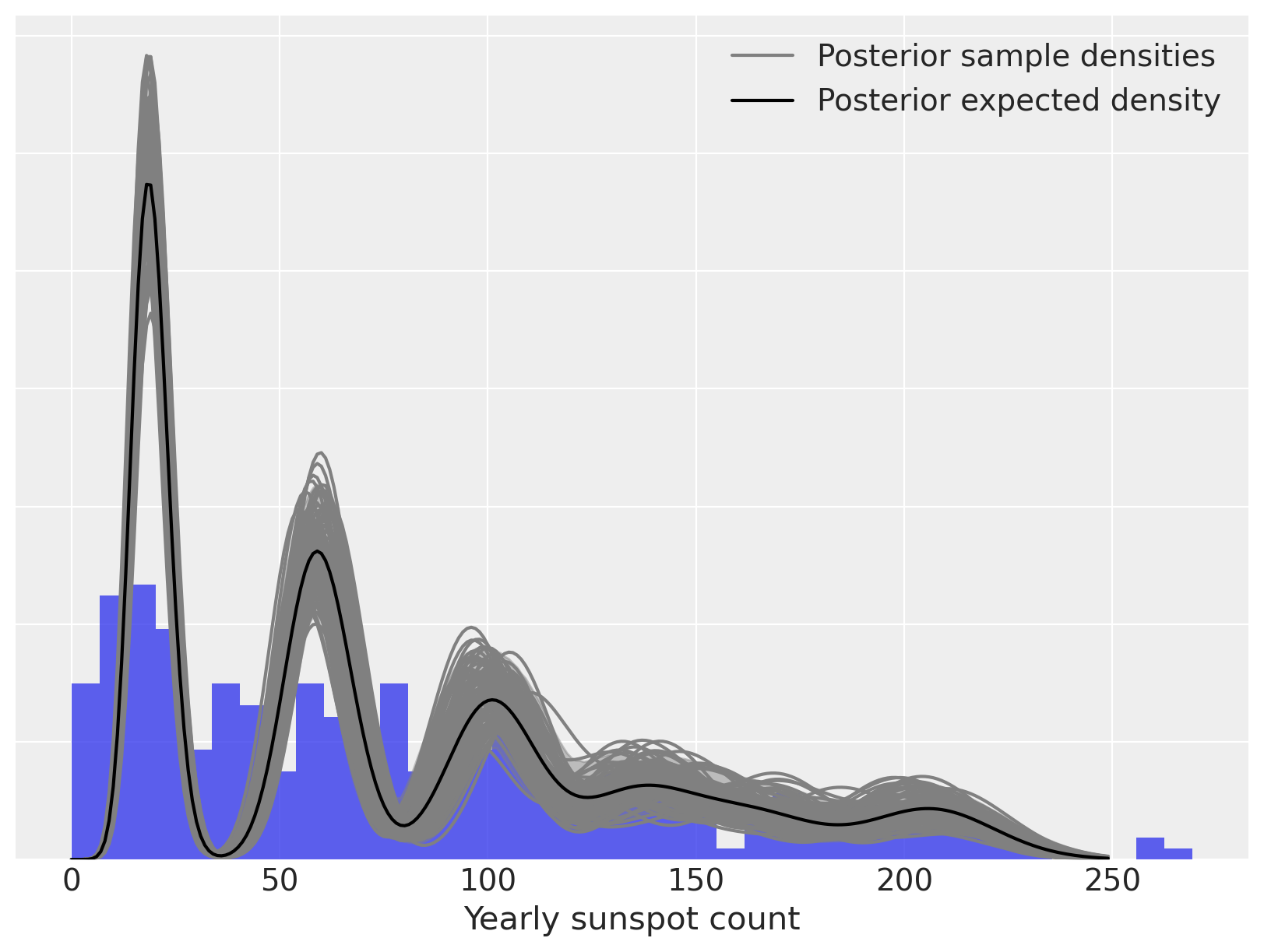
我们现在计算并绘制拟合的密度估计。
x_plot = xr.DataArray(np.arange(250), dims=["plot"])
post_pmf_contribs = xr.apply_ufunc(sp.stats.poisson.pmf, x_plot, trace.posterior["lambda_"])
post_pmfs = (trace.posterior["w"] * post_pmf_contribs).sum(dim=("component"))
post_pmf_quantiles = post_pmfs.quantile([0.025, 0.975], dim=("chain", "draw"))
fig, ax = plt.subplots(figsize=(8, 6))
ax.hist(sunspot_df["sunspot.year"].values, bins=40, density=True, lw=0, alpha=0.75)
ax.fill_between(
x_plot,
post_pmf_quantiles.sel(quantile=0.025),
post_pmf_quantiles.sel(quantile=0.975),
color="gray",
alpha=0.45,
)
ax.plot(x_plot, post_pmfs.sel(chain=0, draw=0), c="gray", label="Posterior sample densities")
ax.plot(
x_plot,
az.extract(post_pmfs, var_names="x", num_samples=100),
c="gray",
)
ax.plot(x_plot, post_pmfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.set_xlabel("Yearly sunspot count")
ax.set_yticklabels([])
ax.legend(loc=1);
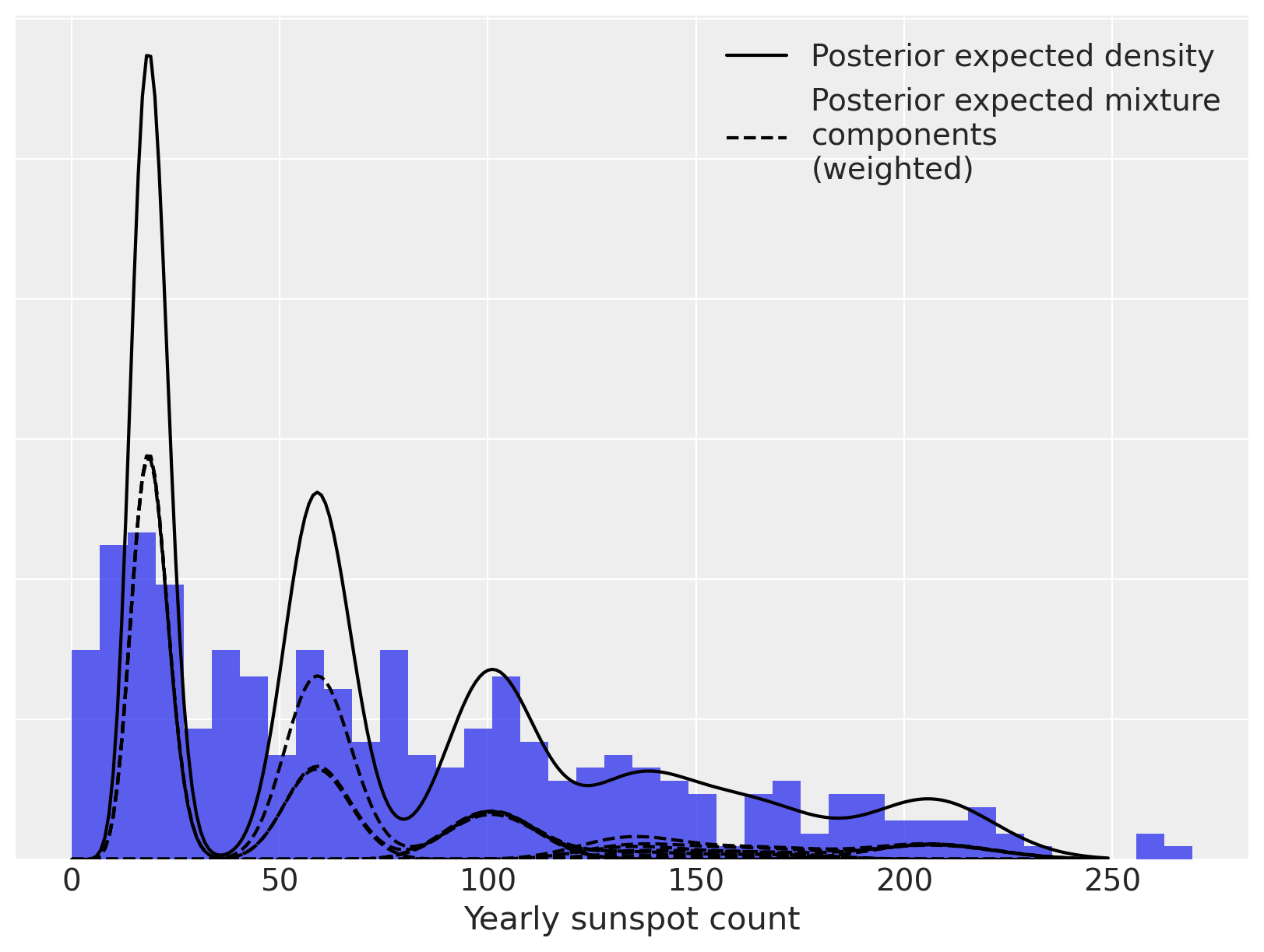
再次,我们可以将后验期望密度分解为加权混合密度。
fig, ax = plt.subplots(figsize=(8, 6))
n_bins = 40
ax.hist(sunspot_df["sunspot.year"].values, bins=n_bins, density=True, color="C0", lw=0, alpha=0.75)
ax.plot(x_plot, post_pmfs.mean(dim=("chain", "draw")), c="k", label="Posterior expected density")
ax.plot(
x_plot,
(trace.posterior["w"] * post_pmf_contribs).mean(dim=("chain", "draw")).sel(component=0),
"--",
c="k",
label="Posterior expected mixture\ncomponents\n(weighted)",
)
ax.plot(
x_plot,
(trace.posterior["w"] * post_pmf_contribs).mean(dim=("chain", "draw")).T,
"--",
c="k",
)
ax.set_xlabel("Yearly sunspot count")
ax.set_yticklabels([])
ax.legend(loc=1);
参考资料#
水印#
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Mon Feb 06 2023
Python implementation: CPython
Python version : 3.10.9
IPython version : 8.9.0
numpy : 1.24.1
xarray : 2023.1.0
pandas : 1.5.3
matplotlib: 3.6.3
arviz : 0.14.0
pymc : 5.0.1
pytensor : 2.8.11
scipy : 1.10.0
seaborn : 0.12.2
Watermark: 2.3.1