序贯蒙特卡罗#

import arviz as az
import numpy as np
import pymc as pm
import pytensor.tensor as pt

print(f"Running on PyMC v{pm.__version__}")

Running on PyMC v4.0.0b6

az.style.use("arviz-darkgrid")

使用标准MCMC方法从具有多个峰值的分布中采样可能会很困难，甚至是不可能的，因为马尔可夫链通常会陷入其中一个最小值。顺序蒙特卡罗采样器（SMC）是一种改善这个问题的方法。

由于有许多SMC变体，在本笔记本中我们将重点介绍在PyMC中实现的版本。

SMC结合了几个统计学概念，包括重要性采样、退火和MCMC。通过退火，我们指的是使用一个辅助的温度参数来控制采样过程。要了解退火如何帮助，让我们将后验写为：

\[p(\theta \mid y)_{\beta} \propto p(y \mid \theta)^{\beta} \; p(\theta)\]

当 \(\beta=0\) 时，我们有 \(p(\theta \mid y)_{\beta=0}\) 是先验分布，而当 \(\beta=1\) 时，我们恢复了真实的后验分布。我们可以将 \(\beta\) 视为一个旋钮，用于逐渐增强似然性。这在一般情况下是有用的，因为从先验分布中采样通常比从后验分布中采样更容易。因此，我们可以使用 \(\beta\) 来控制从易于采样的分布到较难采样的分布的过渡。

算法的总结如下：

  1. 将 \(\beta\) 初始化为零，并将阶段初始化为零。

  2. 生成N个样本 \(S_{\beta}\) 从先验分布中（因为当 \(\beta = 0\) 时，退火后验分布就是先验分布）。

  3. 增加\(\beta\)以使有效样本大小等于某个预定义值（我们使用\(Nt\)，其中\(t\)默认为0.5）。

  4. 计算一组N个重要性权重 \(W\)。这些权重是根据样本在阶段 \(i+1\) 和阶段 \(i\) 的似然比计算的。

  5. 通过根据\(W\)重新采样来获得\(S_{w}\)。

  6. 使用 \(W\) 来计算提议分布的均值和协方差，即多元正态分布（MVNormal）。

  7. 对于阶段0以外的阶段，使用前一阶段的接受率来估计n_steps。

  8. 运行N个独立的Metropolis-Hastings（IMH）链（每个链的长度为n_steps），每个链从\(S_{w}\)中的不同样本开始。样本是IMH，因为提议均值是前一个后验阶段的，而不是参数空间中的当前点。

  9. 从步骤3重复，直到 \(\beta \ge 1\)。

  10. 最终结果是从后验中抽取的\(N\)个样本的集合

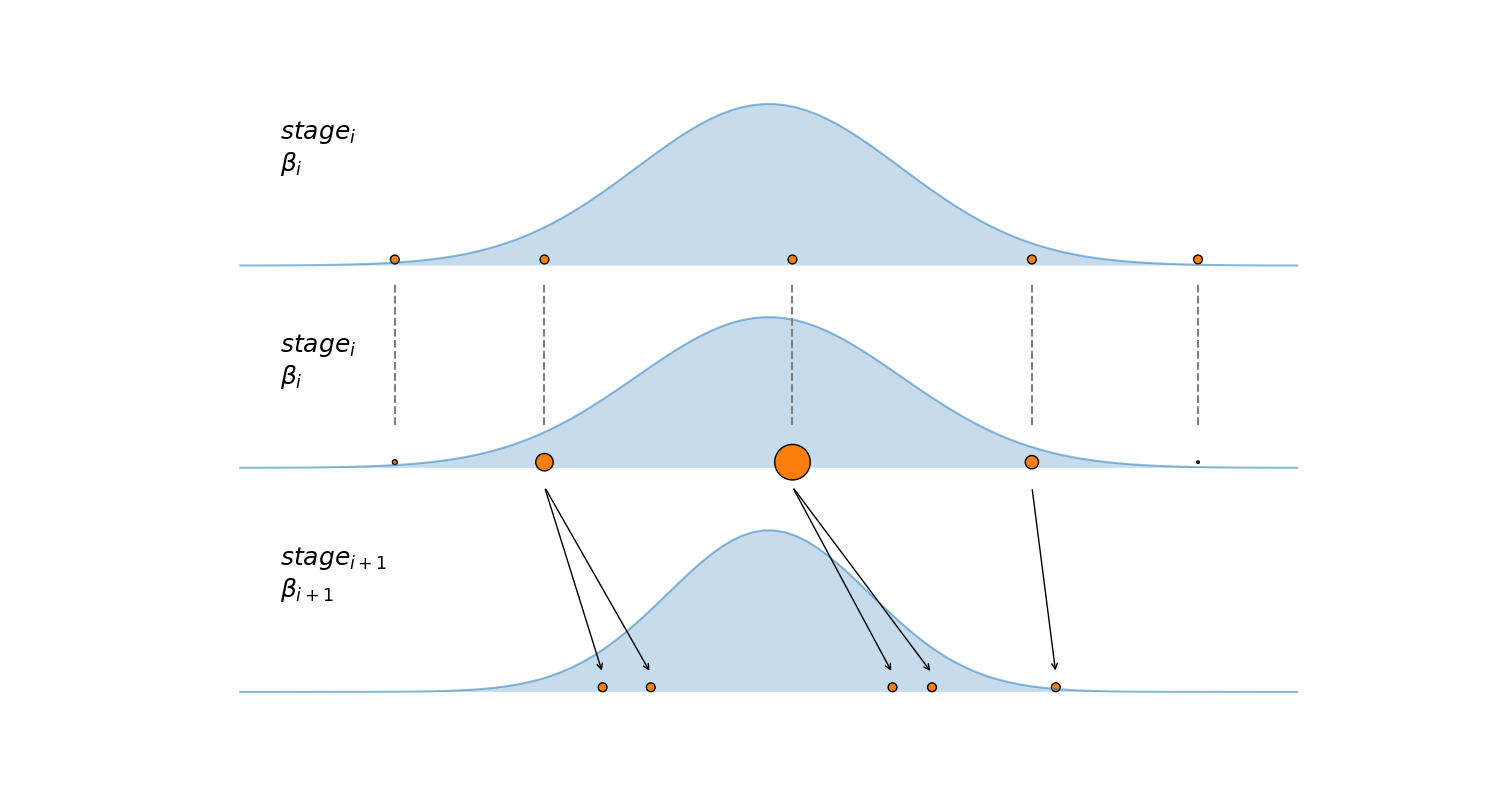
该算法在下图中进行了总结，第一个子图显示了在某个特定阶段的5个样本（橙色点）。第二个子图展示了如何根据这些样本的后验密度（蓝色高斯曲线）对它们进行重新加权。第三个子图展示了从第二个子图中的重新加权样本 \(S_{w}\) 开始，运行一定数量的IMH步骤的结果，注意如何丢弃具有较低后验密度的两个样本（较小的圆圈），并且不使用它们来生成新的马尔可夫链。

SMC阶段

SMC采样器也可以从遗传算法的角度来解释，遗传算法是一种受生物启发的算法，可以概括如下：

  1. 初始化：设置一个个体群体

  2. 变异：个体以某种方式被修改或扰动

  3. 选择：具有高适应度的个体有更高的机会产生后代。

  4. 通过使用从3到1的个体来设置种群。

如果每个个体都是某个问题的特定解，那么遗传算法最终将产生该问题的良好解。一个关键方面是生成足够的多样性（变异步骤），以便探索解空间，从而避免陷入局部最小值。然后我们执行一个选择步骤，以概率性地保留合理的解，同时保持一定的多样性。过于贪婪和短视可能会带来问题，某一时刻的坏解可能会在未来导致好解。

对于在 PyMC 中实现的 SMC 版本，我们使用 draws 参数设置并行马尔可夫链的数量 \(N\)。在每个阶段，SMC 将使用独立的马尔可夫链来探索 退火后验（图中的黑色箭头）。最终的样本，即存储在 trace 中的那些样本，将仅来自最终阶段（\(\beta = 1\)），即 真实 后验（“真实”在数学意义上）。

连续的\(\beta\)值是自动确定的（步骤3）。分布越难采样，两个连续的\(\beta\)值就越接近。并且SMC所需的阶段数也会越多。SMC通过保持两个阶段之间的有效样本大小（ESS）在预定义的常数值（即抽取数量的一半）来计算下一个\(\beta\)值。如果需要，可以通过threshold参数（在区间[0, 1]内）进行调整——当前默认值0.5通常被认为是一个好的默认值。这个值越大，目标ESS越高，两个连续的\(\beta\)值就越接近。这些ESS值是从重要性权重（步骤4）计算得出的，而不是像ArviZ那样从自相关性计算得出的（例如使用az.ess或az.summary）。

另外两个自动确定的参数是：

  • 每个马尔可夫链探索tempered posterior n_steps 的步数。这是从前一阶段的接受率决定的。

  • MVNormal提议分布的协方差也会根据每个阶段的接受率自适应调整。

与其他采样方法一样，多次运行采样器有助于计算诊断信息，SMC也不例外。PyMC将尝试至少运行两个SMC 链（不要与每个SMC链内的\(N\)个马尔可夫链混淆）。

即使SMC在底层使用Metropolis-Hasting算法，它也有几个优于它的优势：

  • 它可以从具有多个峰值的分布中进行采样。

  • 它没有预热期，开始时直接从先验分布中采样，然后在每个阶段，起始点已经根据退火后验分布（由于重新加权步骤）近似分布。

  • 它本质上是并行的。

使用SMC解决PyMC模型#

要查看如何在 PyMC 中使用 SMC 的示例，让我们定义一个具有两个模式的多维高斯分布，维度为 \(n\)，每个模式的权重以及协方差矩阵。

n = 4

mu1 = np.ones(n) * (1.0 / 2)
mu2 = -mu1

stdev = 0.1
sigma = np.power(stdev, 2) * np.eye(n)
isigma = np.linalg.inv(sigma)
dsigma = np.linalg.det(sigma)

w1 = 0.1  # one mode with 0.1 of the mass
w2 = 1 - w1  # the other mode with 0.9 of the mass


def two_gaussians(x):
    log_like1 = (
        -0.5 * n * pt.log(2 * np.pi)
        - 0.5 * pt.log(dsigma)
        - 0.5 * (x - mu1).T.dot(isigma).dot(x - mu1)
    )
    log_like2 = (
        -0.5 * n * pt.log(2 * np.pi)
        - 0.5 * pt.log(dsigma)
        - 0.5 * (x - mu2).T.dot(isigma).dot(x - mu2)
    )
    return pm.math.logsumexp([pt.log(w1) + log_like1, pt.log(w2) + log_like2])

with pm.Model() as model:
    X = pm.Uniform(
        "X",
        shape=n,
        lower=-2.0 * np.ones_like(mu1),
        upper=2.0 * np.ones_like(mu1),
        initval=-1.0 * np.ones_like(mu1),
    )
    llk = pm.Potential("llk", two_gaussians(X))
    idata_04 = pm.sample_smc(2000)

Initializing SMC sampler...
Sampling 4 chains in 4 jobs
100.00% [100/100 00:00<00:00 Stage: 6 Beta: 1.000]

我们可以从消息中看到，PyMC 正在并行运行四个 SMC 链。如前所述，这对于诊断非常有用。与其他采样器一样，一个有用的诊断工具是 plot_trace，这里我们使用 kind="rank_vlines"，因为排名图通常比经典的“轨迹”更有用。

ax = az.plot_trace(idata_04, compact=True, kind="rank_vlines")
ax[0, 0].axvline(-0.5, 0, 0.9, color="k")
ax[0, 0].axvline(0.5, 0, 0.1, color="k")
f'Estimated w1 = {np.mean(idata_04.posterior["X"] < 0).item():.3f}'

'Estimated w1 = 0.907'
../_images/e1c5f4a6a60fa0639e6f98cd2b3682e032cdf6e58d60a1ce248130b3b9b202b1.png

从KDE图可以看出，我们恢复了模式，甚至相对权重看起来也相当不错。右侧的排名图看起来也很好。一条SMC链用蓝色表示，另一条用橙色表示。垂直线表示与理想预期值的偏差，理想预期值用黑色虚线表示。如果垂直线在参考黑色虚线之上，我们得到的样本比预期多；如果垂直线在采样器下方，则得到的样本比预期少。如上图所示的偏差是正常的，不是令人担忧的原因。

如前所述，SMC在内部计算了ESS（从重要性权重）的估计值。这些ESS值对于诊断没有用处，因为它们是一个固定的目标值。我们可以从sample_smc返回的轨迹中计算ESS值，但这也不是一个非常有用的诊断方法，因为ESS值的计算考虑了自相关性，而每个SMC运行/链在构造上具有较低的自相关性，对于大多数问题，ESS值将非常接近总样本数（即抽取数 x 链数）。通常情况下，只有在每个SMC链探索不同模式时，ESS值才会是一个较低的数字，在这种情况下，ESS值将接近模式的数量。

杀死你的宝贝#

SMC并非没有问题，随着问题维度的增加，采样可能会恶化，特别是在多模态后验或层次模型中的奇怪几何形状的情况下。在某种程度上，增加抽取的数量可能会有所帮助。增加参数p_acc_rate的值也是一个好主意。此参数控制如何在每个阶段计算步数。要访问每个阶段的步数，您可以检查trace.report.nsteps。理想情况下，SMC将采取的步数低于n_steps。但如果每个阶段的实际步数是n_steps，对于几个阶段，这可能表明我们也应该增加n_steps。

让我们看看当我们运行与之前相同的模型，但将维度从4增加到80时，SMC的性能如何。

n = 80

mu1 = np.ones(n) * (1.0 / 2)
mu2 = -mu1

stdev = 0.1
sigma = np.power(stdev, 2) * np.eye(n)
isigma = np.linalg.inv(sigma)
dsigma = np.linalg.det(sigma)

w1 = 0.1  # one mode with 0.1 of the mass
w2 = 1 - w1  # the other mode with 0.9 of the mass


def two_gaussians(x):
    log_like1 = (
        -0.5 * n * pt.log(2 * np.pi)
        - 0.5 * pt.log(dsigma)
        - 0.5 * (x - mu1).T.dot(isigma).dot(x - mu1)
    )
    log_like2 = (
        -0.5 * n * pt.log(2 * np.pi)
        - 0.5 * pt.log(dsigma)
        - 0.5 * (x - mu2).T.dot(isigma).dot(x - mu2)
    )
    return pm.math.logsumexp([pt.log(w1) + log_like1, pt.log(w2) + log_like2])

with pm.Model() as model:
    X = pm.Uniform(
        "X",
        shape=n,
        lower=-2.0 * np.ones_like(mu1),
        upper=2.0 * np.ones_like(mu1),
        initval=-1.0 * np.ones_like(mu1),
    )
    llk = pm.Potential("llk", two_gaussians(X))
    idata_80 = pm.sample_smc(2000)

Initializing SMC sampler...
Sampling 4 chains in 4 jobs
100.00% [100/100 00:00<00:00 Stage: 37 Beta: 1.000]

我们看到SMC识别出这是一个更困难的问题，并增加了阶段数量。我们可以看到SMC仍然从两个模式中采样，但现在权重较高的模型被过度采样了（我们得到的相对权重为0.99，而不是0.9）。注意排名图看起来比n=4时更差。

ax = az.plot_trace(idata_80, compact=True, kind="rank_vlines")
ax[0, 0].axvline(-0.5, 0, 0.9, color="k")
ax[0, 0].axvline(0.5, 0, 0.1, color="k")
f'Estimated w1 = {np.mean(idata_80.posterior["X"] < 0).item():.3f}'

'Estimated w1 = 0.991'
../_images/ea5807247603fafc13e329f4e334340ea834a36360a67e0edc7e1f9fdf31b541.png

您可能希望对n=80重复SMC采样，并更改一个或多个默认参数，以查看是否可以改进采样以及采样器计算后验所需的时间。

%load_ext watermark
%watermark -n -u -v -iv -w -p xarray

Last updated: Tue May 31 2022

Python implementation: CPython
Python version       : 3.9.7
IPython version      : 8.3.0

xarray: 2022.3.0

sys   : 3.9.7 (default, Sep 16 2021, 13:09:58) 
[GCC 7.5.0]
arviz : 0.12.0
numpy : 1.21.5
pytensor: 2.6.2
pymc  : 4.0.0b6

Watermark: 2.3.0