采样中的复合步骤#
本笔记本解释了在采样多个随机变量时,pymc.sample 函数中复合步骤的工作原理。我们将回答与复合步骤相关的以下问题:
复合步骤是如何工作的?
当PyMC默认分配步进方法时会发生什么?
如何指定步骤方法?每次迭代应用步骤方法的顺序是什么?是否有办法指定步骤方法的顺序?
混合离散和连续采样器,特别是与HMC/NUTS混合时,存在哪些问题?
多步方法中出现的样本统计量会发生什么?
az.style.use("arviz-darkgrid")
复合步骤#
当对具有多个自由随机变量的模型进行采样时,需要在 pm.sample 函数中使用复合步骤。当涉及复合步骤时,该函数接受一个 step 列表,以生成用于不同随机变量的 methods 列表。例如在以下代码中:
with pm.Model() as m:
rv1 = ... # random variable 1 (continuous)
rv2 = ... # random variable 2 (continuous)
rv3 = ... # random variable 3 (categorical)
#...
step1 = pm.Metropolis([rv1, rv2])
step2 = pm.CategoricalGibbsMetropolis([rv3])
trace = pm.sample(..., step=[step1, step2])
复合步骤现在包含一个方法列表。在每个采样步骤中,它会遍历这些方法,将一个点作为输入。在每个步骤中,会提出一个新的点作为输出,如果被Metropolis-Hastings准则拒绝,则原始输入的点将作为输出保留。
默认的复合步骤#
为了在PyMC中进行马尔可夫链蒙特卡洛(MCMC)采样以生成后验样本,我们指定一个与特定MCMC算法(如Metropolis、切片采样或无回转采样器(NUTS))相对应的步骤方法对象。PyMC的step_methods可以手动分配,也可以由PyMC自动分配。自动分配基于模型中每个变量的属性。一般来说:
二进制变量将被分配给BinaryMetropolis
离散变量将被分配给Metropolis
连续变量将被分配给NUTS
当我们调用 pm.sample(return_inferencedata=False) 时,PyMC 会为每个自由随机变量分配最佳的步进方法。以下面的例子为例
n_ = pytensor.shared(np.asarray([10, 15]))
with pm.Model() as m:
p = pm.Beta("p", 1.0, 1.0)
ni = pm.Bernoulli("ni", 0.5)
k = pm.Binomial("k", p=p, n=n_[ni], observed=4)
trace = pm.sample(10000)
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>NUTS: [p]
>BinaryGibbsMetropolis: [ni]
Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 43 seconds.
模型中有两个我们希望从中采样的自由参数,一个连续变量 p_logodds__ 和一个二元变量 ni。
m.free_RVs
[p, ni]
当我们调用 pm.sample(return_inferencedata=False) 时,PyMC 会为每个变量分配最佳的采样方法。例如,NUTS 被分配给 p_logodds__,而 BinaryGibbsMetropolis 被分配给 ni。
指定复合步骤#
可以为任何变量子集手动指定它们,从而覆盖自动分配,在采样之前:
with m:
step1 = pm.Metropolis([p])
step2 = pm.BinaryMetropolis([ni])
trace = pm.sample(
10000,
step=[step1, step2],
idata_kwargs={
"dims": {"accept": ["step"]},
"coords": {"step": ["Metropolis", "BinaryMetropolis"]},
},
)
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>Metropolis: [p]
>BinaryMetropolis: [ni]
Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 38 seconds.
The number of effective samples is smaller than 25% for some parameters.
point = m.test_point
point
e:\source\repos\pymc3-v4\pymc\model.py:976: FutureWarning: `Model.test_point` has been deprecated. Use `Model.recompute_initial_point(seed=None)`.
warnings.warn(
{'p_logodds__': array(0.), 'ni': array(1, dtype=int64)}
然后传递 point 到第一步方法 pm.Metropolis 用于随机变量 p。
point, state = step1.step(point=point)
point, state
({'p_logodds__': array(0.52418058), 'ni': array(1, dtype=int64)},
[{'tune': True,
'scaling': array([1.]),
'accept': 0.08964089546197954,
'accepted': True}])
如您所见,ni 的值没有改变,但 p_logodds__ 被更新了。
同样地,你可以将更新后的 point 传递给 step2 并获取 ni 的样本:
point = step2.step(point=point)
point
({'p_logodds__': array(0.52418058), 'ni': array(0, dtype=int64)},
[{'tune': True, 'accept': 21.632194762798157, 'p_jump': 0.5}])
复合步骤通过迭代列表中的所有步骤来完全按照这种方式工作。实际上,它是吉布斯采样中的Metropolis Hastings方法。
此外,pm.CompoundStep 在内部由 pm.sample(return_inferencedata=False) 调用。我们可以将它们显式地表示如下:
with m:
comp_step1 = pm.CompoundStep([step1, step2])
trace1 = pm.sample(10000, comp_step1)
comp_step1.methods
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>Metropolis: [p]
>BinaryMetropolis: [ni]
Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 38 seconds.
The number of effective samples is smaller than 25% for some parameters.
[<pymc.step_methods.metropolis.Metropolis at 0x215573b6cd0>,
<pymc.step_methods.metropolis.BinaryMetropolis at 0x21557af7e20>]
# These are the Sample Stats for Compound Step based sampling
list(trace1.sample_stats.data_vars)
['p_jump', 'scaling', 'accepted', 'accept']
注意:在复合步骤方法中,样本统计变量可能同时存在于多个步骤方法中,例如每个链中的accept。
trace1.sample_stats["accept"].sel(chain=1).values
array([[5.05880713e-02, 1.00000000e+00],
[1.00656794e+00, 8.23345217e-01],
[6.44911199e-03, 1.00000000e+00],
...,
[1.32225607e-06, 1.00000000e+00],
[7.07386719e-02, 1.00000000e+00],
[4.94538644e-02, 1.00000000e+00]])
步骤方法的顺序#
在默认设置下,参数更新顺序遵循随机变量的相同顺序,并自动分配。但如果你指定步骤,你可以更改列表中方法的顺序:
with m:
comp_step2 = pm.CompoundStep([step2, step1])
trace2 = pm.sample(
10000,
comp_step2,
)
comp_step2.methods
Multiprocess sampling (4 chains in 4 jobs)
CompoundStep
>BinaryMetropolis: [ni]
>Metropolis: [p]
Sampling 4 chains for 1_000 tune and 10_000 draw iterations (4_000 + 40_000 draws total) took 39 seconds.
The number of effective samples is smaller than 25% for some parameters.
[<pymc.step_methods.metropolis.BinaryMetropolis at 0x21557af7e20>,
<pymc.step_methods.metropolis.Metropolis at 0x215573b6cd0>]
在采样过程中,它总是遵循相同的步骤顺序,以类似吉布斯的方式进行每个样本的更新。更准确地说,在每次更新时,它会遍历methods列表,其中接受/拒绝是基于将接受率与\(p \sim \text{Uniform}(0, 1)\)进行比较(通过检查是否\(\log p < \log p_{\text {updated}} - \log p_{\text {current}}\))。
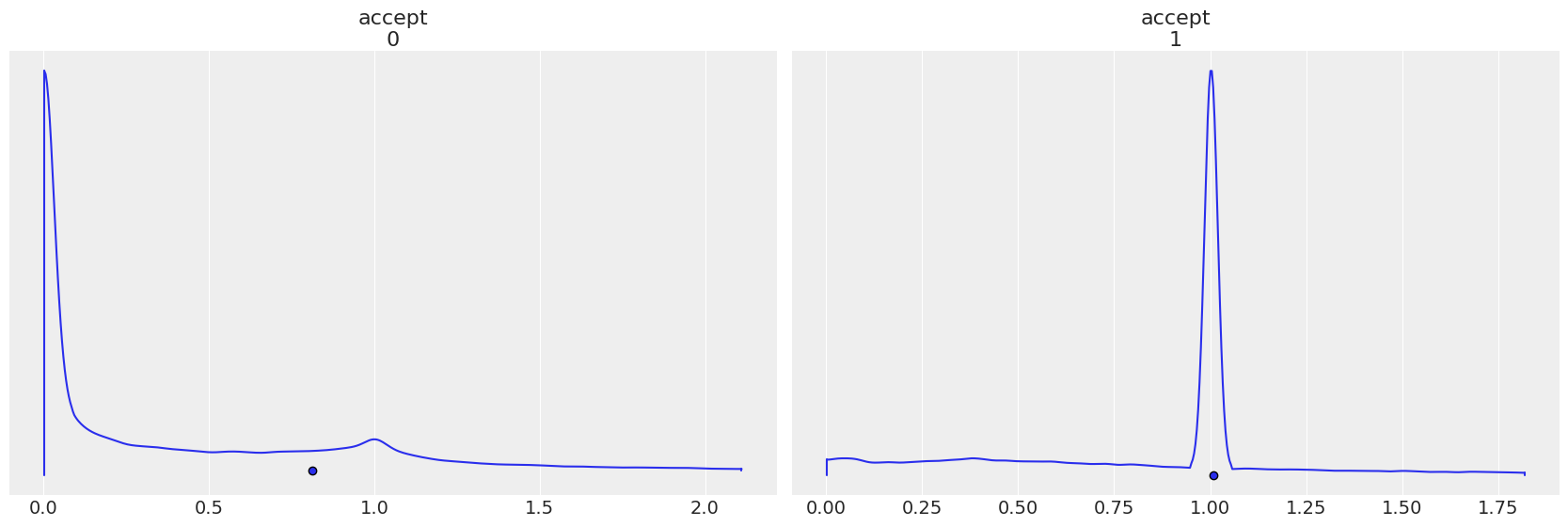
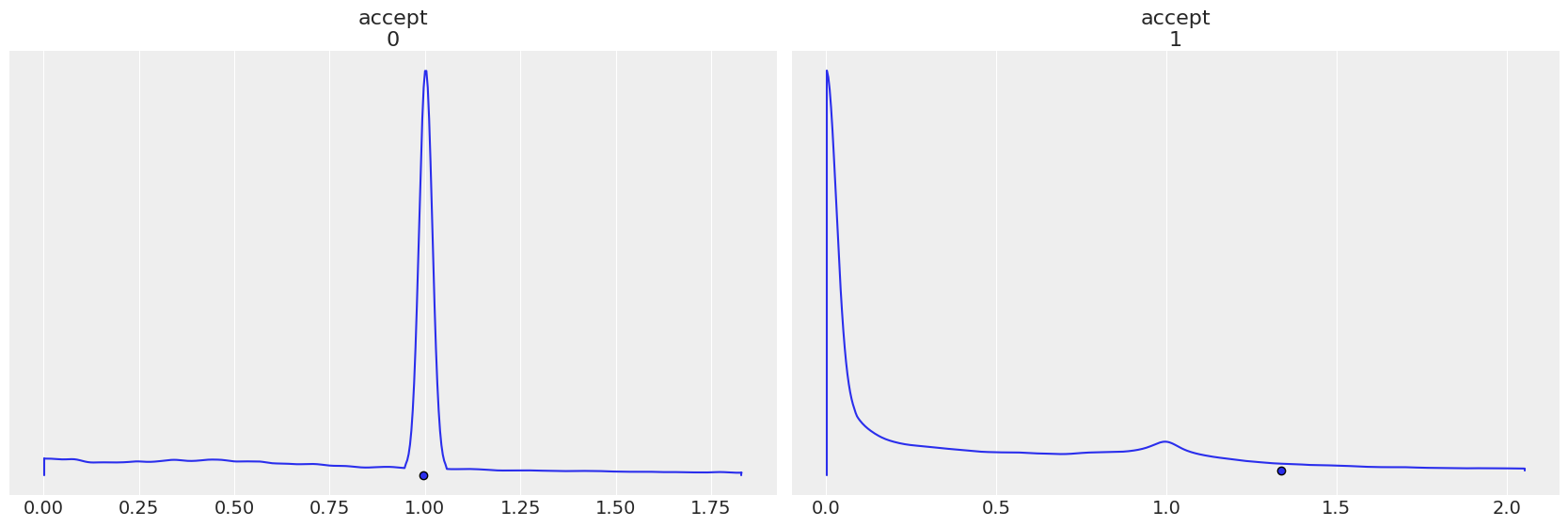
每个步骤方法都有自己的 accept,注意当步骤顺序反转时,图表是如何反转的。
az.plot_density(
trace1,
group="sample_stats",
var_names="accept",
point_estimate="mean",
);
az.plot_density(
trace2,
group="sample_stats",
var_names="accept",
point_estimate="mean",
);
混合离散和连续采样的问题#
一个反复出现的问题/担忧是混合离散和连续采样的有效性,特别是将其他采样器与NUTS混合。虽然在《贝叶斯数据分析》第三版第12.4章中有一小段关于“将哈密尔顿蒙特卡洛与吉布斯采样结合”的内容,这表明这可能是一种有效的方法,但Stan的开发者始终对其在实践中的可行性持怀疑态度。(这里有更多关于这个问题的讨论 1, 2).
混合离散和连续采样的担忧在于,离散参数的变化会影响连续分布的几何形状,从而使得适应(即调整的质量矩阵和步长)可能不适用于哈密顿蒙特卡洛采样。HMC/NUTS对其调整参数(质量矩阵和步长)非常敏感。另一个问题是,当离散参数变化时,我们也不知道需要运行多少次迭代才能得到一个像样的样本。尽管尚未完全评估,但似乎如果离散参数是低维的(例如,2类混合模型,带有显式离散标签的异常值检测),离散采样与HMC/NUTS的混合效果还可以。然而,它比边缘化离散参数的效率要低得多。有时可以观察到马尔可夫链经常卡住。为了更恰当地评估这一点,可以使用基于模拟的方法来查看后验覆盖率并建立计算的正确性,如Cook, Gelman, and Rubin 2006所解释的那样。
更新者:Meenal Jhajharia
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Sun Jan 09 2022
Python implementation: CPython
Python version : 3.8.10
IPython version : 7.30.1
pymc : 4.0.0b1
pytensor: 2.3.2
arviz : 0.11.4
xarray: 0.18.2
numpy : 1.21.1
Watermark: 2.3.0