使用自定义步骤方法从局部共轭后验分布中采样

介绍

基于蒙特卡洛的采样方法在贝叶斯推断中被极其广泛地使用，而PyMC3使用了一种强大的哈密顿蒙特卡洛（HMC）版本，能够高效地从具有数百或数千个参数的后验分布中进行采样。HMC是一种通用的推断算法，因为它不需要假设特定的先验分布（如回归模型条件方差的逆Gamma先验）或似然函数。通常情况下，先验与似然的乘积不容易以封闭形式进行积分，因此我们无法通过纸笔推导出后验的形式。HMC被广泛认为是对先前马尔可夫链蒙特卡洛（MCMC）算法的一项重大改进，因为它利用了模型对数后验密度的梯度，在参数空间中做出有根据的提议。

然而，对于变量和观测数据之间具有特别复杂函数依赖关系的模型，这些梯度计算通常是昂贵的。在这种情况下，我们可能希望通过利用模型某些部分中的附加结构来找到更快的采样方案。当模型中的多个变量是共轭的时，条件后验（即，保持所有其他模型变量固定的后验分布）通常可以非常容易地从中采样。这表明在使用HMC-within-Gibbs步骤时，我们可以在可能的情况下交替使用廉价的共轭采样进行变量采样，并对其余部分使用更昂贵的HMC。

通常情况下，不建议选择任何替代采样方法并用它来替代HMC。这种组合通常在有效采样率方面表现更差，即使单个样本的抽取速度更快。在本笔记本中，我们展示了如何在PyMC3中实现共轭采样方案，并将其与全HMC（或者在这种情况下，NUTS）方法进行比较。对于这种情况，我们发现使用共轭采样可以显著加快Dirichlet-多项式模型的计算速度。

概率模型

为了保持这个笔记本的简洁，我们将考虑一个相对简单的分层模型，该模型定义为跨\(J\)个结果的\(N\)个观测值的计数向量：

\[\tau \sim Exp(\lambda)\]

\[\mathbf{p}_i \sim Dir(\tau )\]

\[\mathbf{x}_i \sim Multinomial(\mathbf{p}_i)\]

索引 \(i\in\{1,...,N\}\) 表示观测值，而 \(j\in \{1...,J\}\) 索引结果。变量 \(\tau\) 是一个标量浓度，而 \(\mathbf{p}_i\) 是一个从狄利克雷先验中抽取的 \(J\) 维概率向量，其条目为 \((\tau, \tau, ..., \tau)\)。在固定的 \(\tau\) 和观测数据 \(x\) 的情况下，我们知道 \(\mathbf{p}\) 具有 封闭形式的后验分布，这意味着我们可以轻松地从中采样。我们的采样方案将在 \(\tau\) 上使用 No-U-Turn 采样器 (NUTS) 和从已知的条件后验分布中抽取 \(\mathbf{p}_i\) 之间交替进行。我们将假设 \(\lambda\) 的固定值。

实现自定义步骤方法

将共轭采样器作为我们复合采样方法的一部分是直接的：我们定义一个新的步骤方法，该方法检查马尔可夫链近似的当前状态，并通过添加从共轭后验中抽取的样本来对其进行修改。

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc3 as pm

from pymc3.distributions.transforms import stick_breaking
from pymc3.model import modelcontext
from pymc3.step_methods.arraystep import BlockedStep

RANDOM_SEED = 8927
np.random.seed(RANDOM_SEED)
az.style.use("arviz-darkgrid")

首先，我们需要一种从狄利克雷分布中采样的方法。内置的 numpy.random.dirichlet 只能处理二维输入数组，而我们可能希望在未来将其推广到更广泛的用途。因此，我创建了一个函数，通过将参数数组 c 表示为伽马随机变量的归一化和来从狄利克雷分布中采样。更多关于这方面的细节可以在这里找到。

def sample_dirichlet(c):
    """
    Samples Dirichlet random variables which sum to 1 along their last axis.
    """
    gamma = np.random.gamma(c)
    p = gamma / gamma.sum(axis=-1, keepdims=True)
    return p

接下来，我们定义用于替换部分计算的NUTS的步骤对象。它必须有一个step方法，该方法接收一个名为point的字典，其中包含马尔可夫链的当前状态。我们将在原地修改它。

这里有一个额外的复杂性，因为PyMC3并不以\(\mathbf{p}=(p_1, p_2 ,..., p_J)\)的形式跟踪Dirichlet随机变量的状态，并带有约束\(\sum_j p_j = 1\)。相反，它使用了一个逆向的stick breaking变换，这种变换更容易与NUTS一起使用。这种变换去除了所有条目必须总和为1且为正的约束。

class ConjugateStep(BlockedStep):
    def __init__(self, var, counts: np.ndarray, concentration):
        self.vars = [var]
        self.counts = counts
        self.name = var.name
        self.conc_prior = concentration

    def step(self, point: dict):
        # Since our concentration parameter is going to be log-transformed
        # in point, we invert that transformation so that we
        # can get conc_posterior = conc_prior + counts
        conc_posterior = np.exp(point[self.conc_prior.transformed.name]) + self.counts
        draw = sample_dirichlet(conc_posterior)

        # Since our new_p is not in the transformed / unconstrained space,
        # we apply the transformation so that our new value
        # is consistent with PyMC3's internal representation of p
        point[self.name] = stick_breaking.forward_val(draw)

        return point

这里point的使用及其索引变量可能会让人感到困惑。特别是表达式point[self.conc_prior.transformed.name]非常长。这个表达式是必要的，因为当调用step时，它会传递一个字典point，其中字符串变量名作为键。

然而，先验参数的名称不会直接存储在 point 的键中，因为 PyMC3 存储的是一个转换后的变量。因此，我们需要使用 转换后的名称 来查询 point，然后撤销该转换。

为了识别正确的变量以查询到point，我们需要在初始化时传入一个参数，该参数告诉采样步骤在哪里找到先验参数。因此，我们将var传递给ConjugateStep，以便采样器稍后可以找到转换后的变量的名称（var.transformed.name）。

模拟数据

我们将在一些模拟数据上尝试使用采样器。固定 \(\tau=0.5\)，我们将从10维狄利克雷分布中抽取500个观测值。

J = 10
N = 500

ncounts = 20
tau_true = 0.5
alpha = tau_true * np.ones([N, J])
p_true = sample_dirichlet(alpha)
counts = np.zeros([N, J])

for i in range(N):
    counts[i] = np.random.multinomial(ncounts, p_true[i])
print(counts.shape)

(500, 10)

部分共轭与完整NUTS采样的比较

我们没有关于\(\tau\)的后验分布的封闭形式表达式，因此我们将对其使用NUTS。在下面的代码单元中，我们使用以下两种方法拟合相同的模型：1) 对概率向量使用共轭采样，并对\(\tau\)使用NUTS，以及2) 对所有内容使用NUTS。

traces = []
models = []
names = ["Partial conjugate sampling", "Full NUTS"]

for use_conjugate in [True, False]:
    with pm.Model() as model:
        tau = pm.Exponential("tau", lam=1, testval=1.0)
        alpha = pm.Deterministic("alpha", tau * np.ones([N, J]))
        p = pm.Dirichlet("p", a=alpha)

        if use_conjugate:
            # If we use the conjugate sampling, we don't need to define the likelihood
            # as it's already taken into account in our custom step method
            step = [ConjugateStep(p.transformed, counts, tau)]

        else:
            x = pm.Multinomial("x", n=ncounts, p=p, observed=counts)
            step = []

        trace = pm.sample(step=step, chains=2, cores=1, return_inferencedata=True)
        traces.append(trace)

    assert all(az.summary(trace)["r_hat"] < 1.1)
    models.append(model)

Sequential sampling (2 chains in 1 job)
CompoundStep
>ConjugateStep: [p]
>NUTS: [tau]

100.00% [2000/2000 00:13<00:00 Sampling chain 0, 0 divergences]

100.00% [2000/2000 00:07<00:00 Sampling chain 1, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 20 seconds.
The number of effective samples is smaller than 25% for some parameters.
Sequential sampling (2 chains in 1 job)
NUTS: [p, tau]

100.00% [2000/2000 04:09<00:00 Sampling chain 0, 0 divergences]

100.00% [2000/2000 02:50<00:00 Sampling chain 1, 0 divergences]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 420 seconds.
The estimated number of effective samples is smaller than 200 for some parameters.

我们看到部分共轭采样的运行时间要低得多，但如果样本具有高自相关性或链混合非常缓慢，这可能会产生误导。我们还看到在仅使用NUTS的跟踪中有一些分歧。

我们希望确保这两个采样器收敛到相同的估计值。下面的后验直方图和轨迹图显示，两者基本上都在合理的后验不确定性可信区间内收敛到\(\tau\)。我们还可以看到，轨迹图缺乏任何明显的自相关性，因为它们大多与白噪声无法区分。

for name, trace in zip(names, traces):
    ax = az.plot_trace(trace, var_names="tau")
    ax[0, 0].axvline(0.5, label="True value", color="k")
    ax[0, 0].legend()
    plt.suptitle(name)

我们希望避免以每秒原始样本数来比较采样器的效率。如果一个采样器每个样本处理速度很快，但生成的样本高度相关，那么有效样本大小（ESS）就会减少。由于我们的后验分析在很大程度上依赖于有效样本大小，因此我们应该检查后者的数量。

该模型包括 \(500\times 10=5000\) 个概率值，用于500个狄利克雷随机变量。让我们计算这5000个条目的有效样本大小，并为每种采样方法生成一个直方图：

summaries_p = []
for trace, model in zip(traces, models):
    with model:
        summaries_p.append(az.summary(trace, var_names="p"))

[plt.hist(s["ess_mean"], bins=50, alpha=0.4, label=names[i]) for i, s in enumerate(summaries_p)]
plt.legend(), plt.xlabel("Effective sample size");

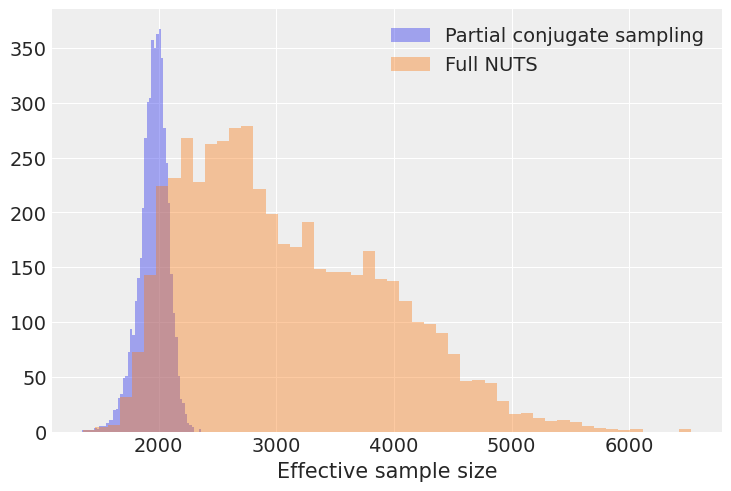
有趣的是，我们看到尽管完整NUTS运行的ESS直方图的模式较大，但最小ESS似乎较低。由于我们的推断通常受限于马尔可夫链中表现最差的部分，因此最小ESS是值得关注的。

print("Minimum effective sample sizes across all entries of p:")
print({names[i]: s["ess_mean"].min() for i, s in enumerate(summaries_p)})

Minimum effective sample sizes across all entries of p:
{'Partial conjugate sampling': 1351.0, 'Full NUTS': 1358.0}

在这里，我们可以看到共轭采样方案在最坏情况下获得了相似的有效样本数量。然而，当我们考虑有效采样的速率时，存在巨大的差异。

print("Minimum ESS/second across all entries of p:")
print(
    {
        names[i]: s["ess_mean"].min() / traces[i].posterior.sampling_time
        for i, s in enumerate(summaries_p)
    }
)

Minimum ESS/second across all entries of p:
{'Partial conjugate sampling': 66.60434089978705, 'Full NUTS': 3.233159737125047}

部分共轭采样方案在最坏情况下的有效样本大小（ESS）率方面快了10倍以上！

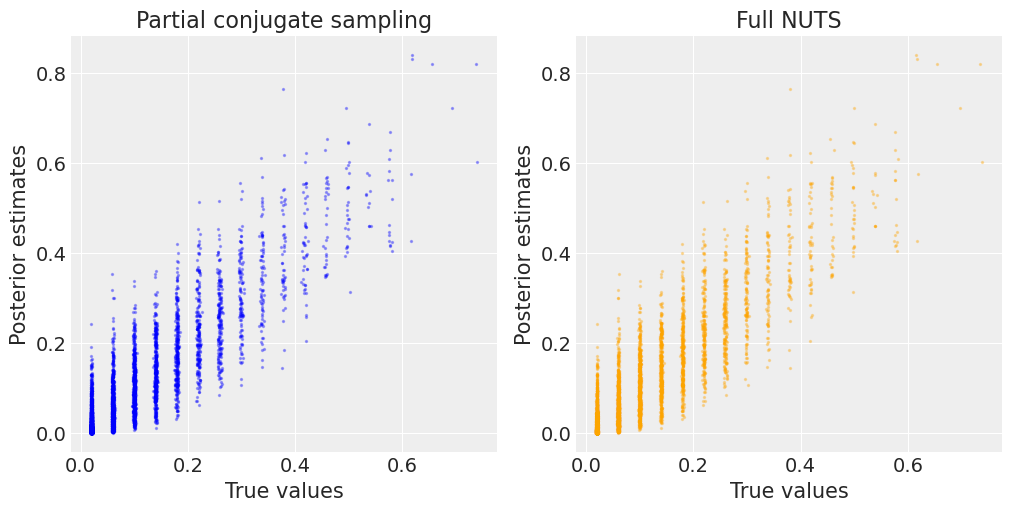
作为最后的检查，我们也希望确保两种采样器的概率估计是相同的。在下图中，我们可以看到来自部分共轭采样和完整NUTS采样的估计值与真实值非常接近。

fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].scatter(
    summaries_p[0]["mean"],
    p_true.ravel(),
    s=2,
    label="Partial conjugate sampling",
    zorder=2,
    alpha=0.3,
    color="b",
)
axes[0].set_ylabel("Posterior estimates"), axes[0].set_xlabel("True values")

axes[1].scatter(
    summaries_p[1]["mean"],
    p_true.ravel(),
    s=2,
    alpha=0.3,
    color="orange",
)
axes[1].set_ylabel("Posterior estimates"), axes[1].set_xlabel("True values")

[axes[i].set_title(n) for i, n in enumerate(names)];

• 本笔记本由Christopher Krapu于2020年11月17日编写。

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sun Jan 17 2021

Python implementation: CPython
Python version       : 3.8.5
IPython version      : 7.19.0

numpy     : 1.19.2
arviz     : 0.10.0
pymc3     : 3.10.0
matplotlib: 3.3.3

Watermark: 2.1.0