审查数据模型#
from copy import copy
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pymc as pm
import seaborn as sns
from numpy.random import default_rng
%config InlineBackend.figure_format = 'retina'
rng = default_rng(1234)
az.style.use("arviz-darkgrid")
这个关于贝叶斯生存分析的示例笔记本涉及到了审查数据的问题。审查是一种缺失数据问题,其中大于某个阈值的观测值被截断到该阈值,或小于某个阈值的观测值被截断到该阈值,或两者兼有。这些分别称为右审查、左审查和区间审查。在这个示例笔记本中,我们考虑区间审查。
审查数据出现在许多建模问题中。两个常见的例子是:
生存分析:在研究某种医疗治疗对生存时间的影响时,不可能将研究延长到所有受试者都死亡为止。在研究结束时,许多患者收集到的唯一数据是他们在治疗后存活了一段时间 \(T\):实际上,他们的真实生存时间大于 \(T\)。
传感器饱和:传感器可能有一个有限的范围,上下限仅仅是传感器能够报告的最高和最低值。例如,许多水银温度计只能报告一个非常窄的温度范围。
这个示例笔记本介绍了在PyMC3中处理截断数据的两
一个插补的删失模型,它将删失数据表示为参数,并为所有删失值生成合理的值。由于这种插补,该模型能够生成合理的插补值集,这些值原本会被删失。每个删失元素引入一个随机变量。
一个未插补的删失模型,其中删失数据被积分出去,仅通过对数似然来考虑。该方法更适当地处理大量删失数据,并且收敛更快。
为了建立一个基线,我们与未审查数据的未审查模型进行比较。
# Produce normally distributed samples
size = 500
true_mu = 13.0
true_sigma = 5.0
samples = rng.normal(true_mu, true_sigma, size)
# Set censoring limits
low = 3.0
high = 16.0
def censor(x, low, high):
x = copy(x)
x[x <= low] = low
x[x >= high] = high
return x
# Censor samples
censored = censor(samples, low, high)
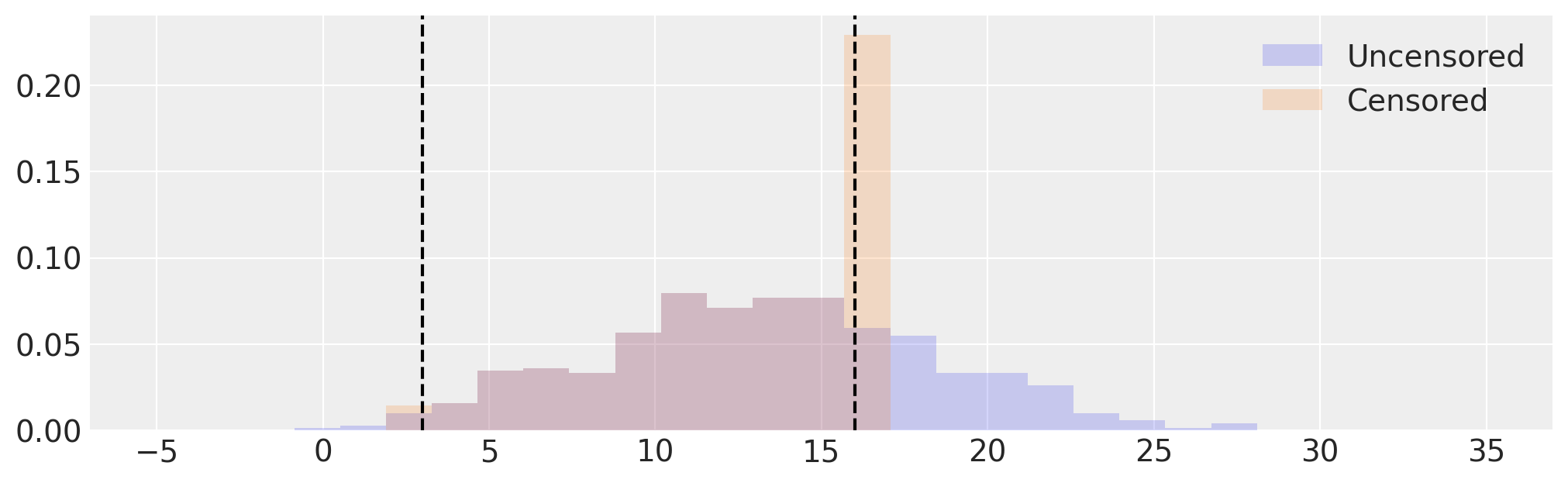
# Visualize uncensored and censored data
_, ax = plt.subplots(figsize=(10, 3))
edges = np.linspace(-5, 35, 30)
ax.hist(samples, bins=edges, density=True, histtype="stepfilled", alpha=0.2, label="Uncensored")
ax.hist(censored, bins=edges, density=True, histtype="stepfilled", alpha=0.2, label="Censored")
[ax.axvline(x=x, c="k", ls="--") for x in [low, high]]
ax.legend();
未审查模型#
我们应该预测,在未审查的数据上运行未审查的模型,我们将得到合理的均值和方差的估计。
uncensored_model_1 = uncensored_model(samples)
with uncensored_model_1:
idata = pm.sample()
az.plot_posterior(idata, ref_val=[true_mu, true_sigma], round_to=3);
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 4 seconds.
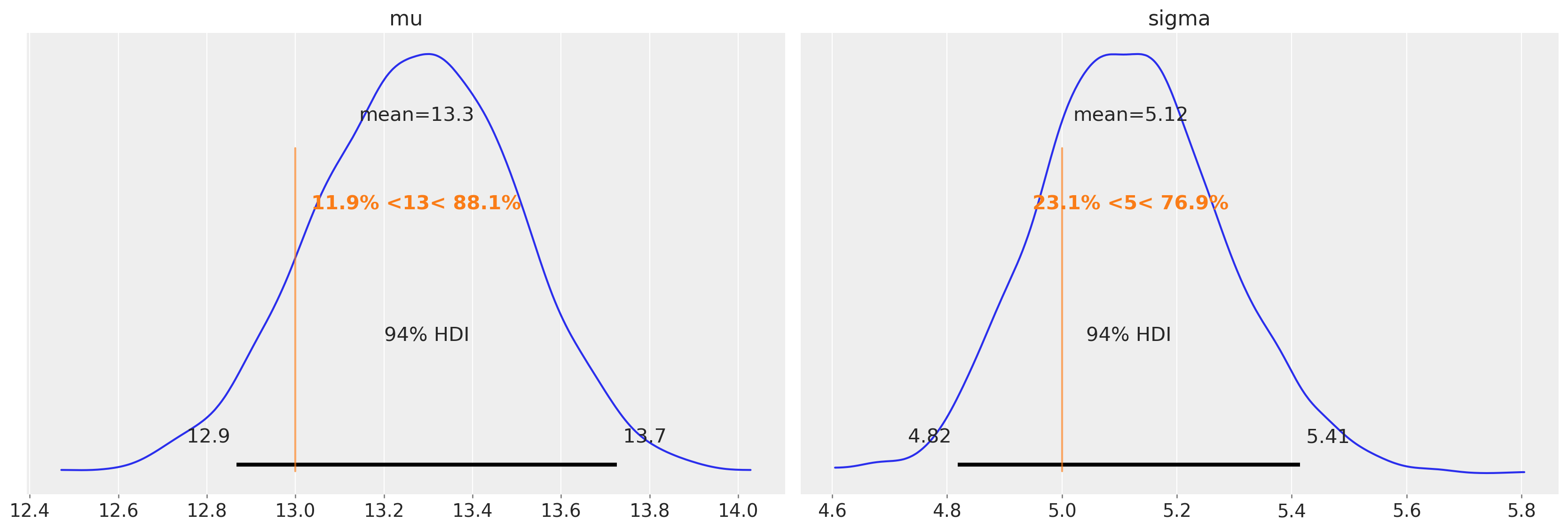
而这正是我们所发现的。
然而,问题在于在审查数据的情况下,我们无法访问真实值。如果我们对审查数据使用相同的未审查模型,我们预计参数估计会有偏差。如果我们计算均值和标准差的点估计,那么我们可以看到我们可能会低估这个特定数据集和审查边界的均值和标准差。
uncensored_model_2 = uncensored_model(censored)
with uncensored_model_2:
idata = pm.sample()
az.plot_posterior(idata, ref_val=[true_mu, true_sigma], round_to=3);
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 4 seconds.
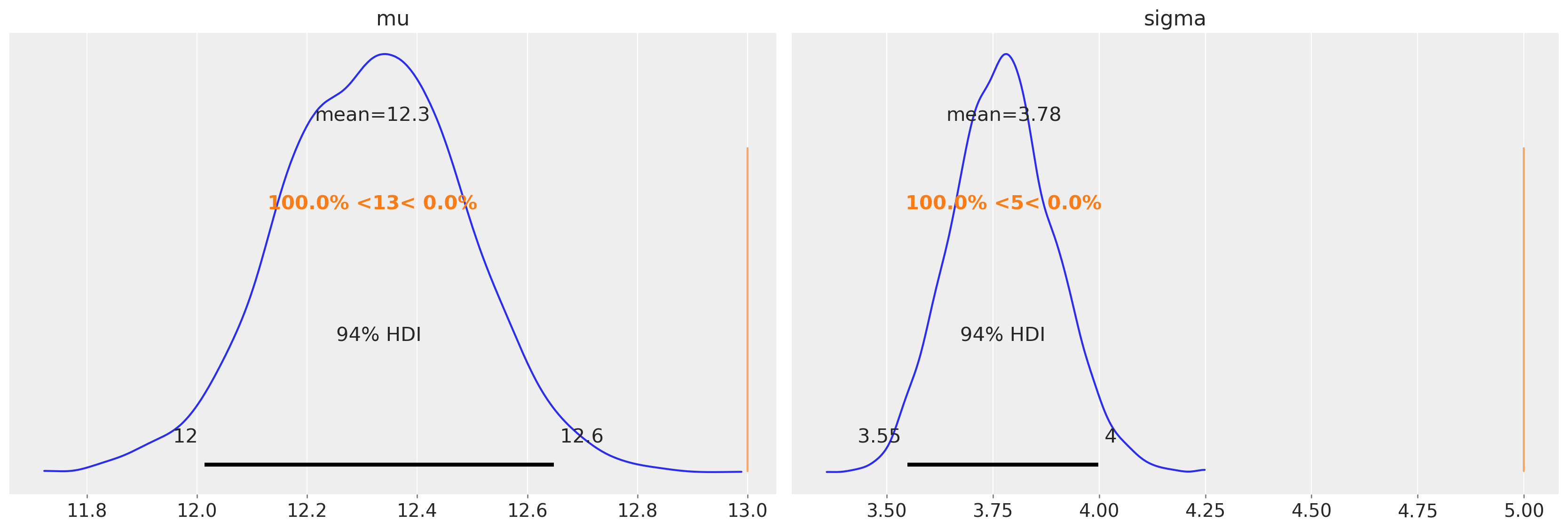
上图证实了这一点。
审查数据模型#
下面的模型展示了处理截尾数据的两种方法。首先,我们需要进行一些数据预处理,以计算左截尾或右截尾的观测数量。我们还需要提取我们观察到的非截尾数据。
模型1 - 删失数据的插补删失模型#
在这个模型中,我们从与未删失数据相同的分布中填补删失值。从后验分布中采样生成可能的未删失数据集。
n_right_censored = sum(censored >= high)
n_left_censored = sum(censored <= low)
n_observed = len(censored) - n_right_censored - n_left_censored
uncensored = censored[(censored > low) & (censored < high)]
assert len(uncensored) == n_observed
with pm.Model() as imputed_censored_model:
mu = pm.Normal("mu", mu=((high - low) / 2) + low, sigma=(high - low))
sigma = pm.HalfNormal("sigma", sigma=(high - low) / 2.0)
right_censored = pm.Normal(
"right_censored",
mu,
sigma,
transform=pm.distributions.transforms.Interval(high, None),
shape=int(n_right_censored),
initval=np.full(n_right_censored, high + 1),
)
left_censored = pm.Normal(
"left_censored",
mu,
sigma,
transform=pm.distributions.transforms.Interval(None, low),
shape=int(n_left_censored),
initval=np.full(n_left_censored, low - 1),
)
observed = pm.Normal("observed", mu=mu, sigma=sigma, observed=uncensored, shape=int(n_observed))
idata = pm.sample()
az.plot_posterior(idata, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma], round_to=3);
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, sigma, right_censored, left_censored]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 17 seconds.
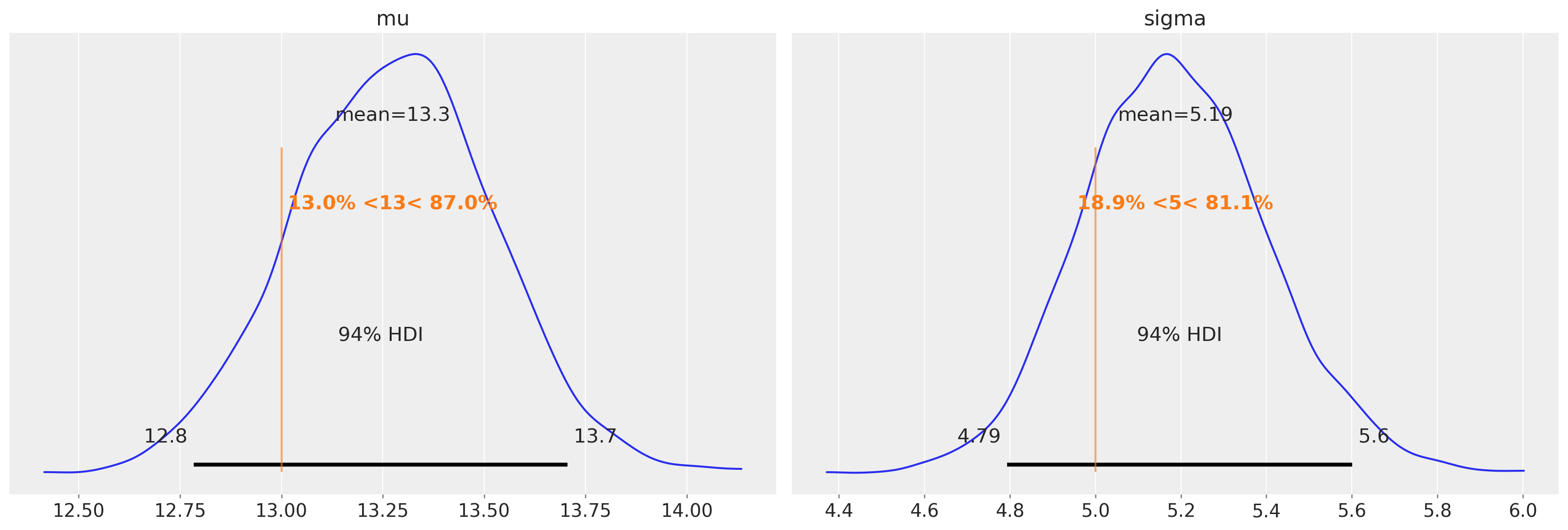
我们可以看到,在未审查的模型中存在的均值和方差估计的偏差已基本消除。
模型2 - 未填补的删失数据模型#
在这里,我们可以利用 pm.Censored。
with pm.Model() as unimputed_censored_model:
mu = pm.Normal("mu", mu=0.0, sigma=(high - low) / 2.0)
sigma = pm.HalfNormal("sigma", sigma=(high - low) / 2.0)
y_latent = pm.Normal.dist(mu=mu, sigma=sigma)
obs = pm.Censored("obs", y_latent, lower=low, upper=high, observed=censored)
采样
with unimputed_censored_model:
idata = pm.sample()
az.plot_posterior(idata, var_names=["mu", "sigma"], ref_val=[true_mu, true_sigma], round_to=3);
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [mu, sigma]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 5 seconds.
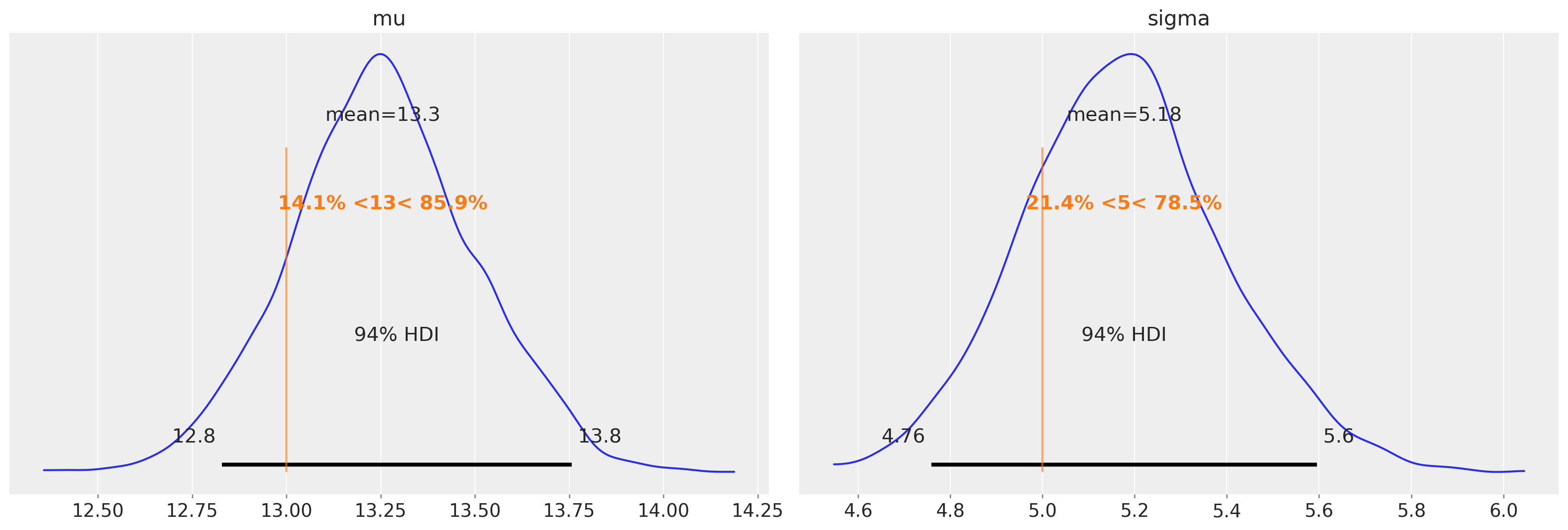
再次强调,均值和方差估计中的偏差(在未审查模型中存在)已基本消除。
讨论#
正如我们所见,两个删失模型似乎都能捕捉到潜在分布的均值和方差,就像未删失模型一样!此外,插补删失模型能够生成删失值的数据集(从left_censored和right_censored的后验中采样以生成它们),而未插补的删失模型在处理更多删失数据时扩展性更好,并且收敛更快。
水印#
%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor,aeppl
Last updated: Tue Jan 17 2023
Python implementation: CPython
Python version : 3.11.0
IPython version : 8.8.0
pytensor: 2.9.1
aeppl : not installed
seaborn : 0.12.2
pymc : 5.0.1+42.g99dd7158
arviz : 0.14.0
matplotlib: 3.6.2
sys : 3.11.0 | packaged by conda-forge | (main, Oct 25 2022, 06:24:40) [GCC 10.4.0]
numpy : 1.24.1
Watermark: 2.3.1
许可证声明#
本示例库中的所有笔记本均在MIT许可证下提供,该许可证允许修改和重新分发,前提是保留版权和许可证声明。
引用 PyMC 示例#
要引用此笔记本,请使用Zenodo为pymc-examples仓库提供的DOI。
重要
许多笔记本是从其他来源改编的:博客、书籍……在这种情况下,您应该引用原始来源。
同时记得引用代码中使用的相关库。
这是一个BibTeX的引用模板:
@incollection{citekey,
author = "<notebook authors, see above>",
title = "<notebook title>",
editor = "PyMC Team",
booktitle = "PyMC examples",
doi = "10.5281/zenodo.5654871"
}
渲染后可能看起来像: