在CEC2006问题上进行扩展蚁群优化的基准测试#
在本教程中,我们将展示如何使用pygmo运行gaco算法,并使用在加拿大温哥华举行的CEC-06约束实参数优化特别会议上使用的测试问题套件进行基准测试。
所有的CEC 2006问题都是盒约束的、连续的、单目标约束问题,并且由pygmo在类cec2006中作为UDP(用户定义问题)提供。
我们现在想要对三种用户定义的算法进行基准测试。由于这是一个约束问题,我们需要一个能够处理约束的UDA(用户定义算法)。在这方面,我们可以利用pygmo的元算法cstrs_self_adaptive,
以允许任何UDA用于约束问题。因此,我们将对扩展的蚁群优化算法gaco、相同的算法以及自适应的差分进化算法sade进行基准测试,两者都结合了自适应的约束处理技术。
特别是,我们将在24个CEC2006问题中的6个问题上使用上述三个UDAs(即问题:13、14、15、16、17、18)。这些问题的最佳已知适应度可以在技术报告:“CEC 2006约束实参数优化特别会议的问题定义和评估标准”中找到,作者是J. J. Liang等人,2006年。 为了在这些问题上运行UDAs,我们可以编写以下代码:
>>> import pygmo as pg
>>> #we first save the best known solutions in a vector:
>>> real_minima=[0.0539415140, -47.7648884595, 961.7150222899, -1.9051552586, 8853.5396748064, -0.8660254038]
>>> #we instantiate the problems
>>> problems=[pg.cec2006(13), pg.cec2006(14), pg.cec2006(15), pg.cec2006(16), pg.cec2006(17), pg.cec2006(18)]
>>> for index in range(0,6):
... #we extract the problem of the case:
... udp = problems[index]
... prob = pg.problem(udp)
... #Instantiate pagmo algorithms:
... uda_gaco = pg.gaco(550, 100, 1.0, real_minima[index], 0.0, 200, 7, 10000, 10000, 0.0, False, 23)
... uda_cstrs_sade=pg.cstrs_self_adaptive(40,pg.sade(10, 2, 1, 1e-6, 1e-6, False, 23))
... uda_cstrs_gaco=pg.cstrs_self_adaptive(40,pg.gaco(10, 125, 1.0, real_minima[index], 0.0, 8, 7, 10000, 10000, 0.0, False, 23))
... algo_gaco=pg.algorithm(uda_gaco)
... algo_cstrs_sade=pg.algorithm(uda_cstrs_sade)
... algo_cstrs_gaco=pg.algorithm(uda_cstrs_gaco)
... #Set the seed for reproducibility purposes:
... algo_gaco.set_seed(23)
... algo_cstrs_sade.set_seed(23)
... algo_cstrs_gaco.set_seed(23)
... #Instantiate populations:
... pop_gaco = pg.population(prob, size=100, seed=23)
... pop_cstrs_sade = pg.population(prob, size=125, seed=23)
... pop_cstrs_gaco = pg.population(prob, size=125, seed=23)
... #Set verbosity:
... algo_gaco.set_verbosity(5)
... algo_cstrs_sade.set_verbosity(1)
... algo_cstrs_gaco.set_verbosity(1)
... #Run the evolution:
... pop_gaco=algo_gaco.evolve(pop_gaco)
... pop_cstrs_sade=algo_cstrs_sade.evolve(pop_cstrs_sade)
... pop_cstrs_gaco=algo_cstrs_gaco.evolve(pop_cstrs_gaco)
... #Extract the log:
... uda_gaco=algo_gaco.extract(pg.gaco)
... uda_sa_sade=algo_cstrs_sade.extract(pg.cstrs_self_adaptive)
... uda_sa_gaco=algo_cstrs_gaco.extract(pg.cstrs_self_adaptive)
... #The logs are saved for each problem:
... if (index==0):
... log_gaco_P13=uda_gaco.get_log()
... log_sa_sade_P13=uda_sa_sade.get_log()
... log_sa_gaco_P13=uda_sa_gaco.get_log()
... elif (index==1):
... log_gaco_P14=uda_gaco.get_log()
... log_sa_sade_P14=uda_sa_sade.get_log()
... log_sa_gaco_P14=uda_sa_gaco.get_log()
... elif (index==2):
... log_gaco_P15=uda_gaco.get_log()
... log_sa_sade_P15=uda_sa_sade.get_log()
... log_sa_gaco_P15=uda_sa_gaco.get_log()
... elif (index==3):
... log_gaco_P16=uda_gaco.get_log()
... log_sa_sade_P16=uda_sa_sade.get_log()
... log_sa_gaco_P16=uda_sa_gaco.get_log()
... elif (index==4):
... log_gaco_P17=uda_gaco.get_log()
... log_sa_sade_P17=uda_sa_sade.get_log()
... log_sa_gaco_P17=uda_sa_gaco.get_log()
... elif (index==5):
... log_gaco_P18=uda_gaco.get_log()
... log_sa_sade_P18=uda_sa_sade.get_log()
... log_sa_gaco_P18=uda_sa_gaco.get_log()
在这种情况下,我们使用100个个体的种群和550代来运行gaco,而我们使用cstrs_self_adaptive运行gaco和sade进行40次迭代,每次迭代有10代和125个个体在种群中。
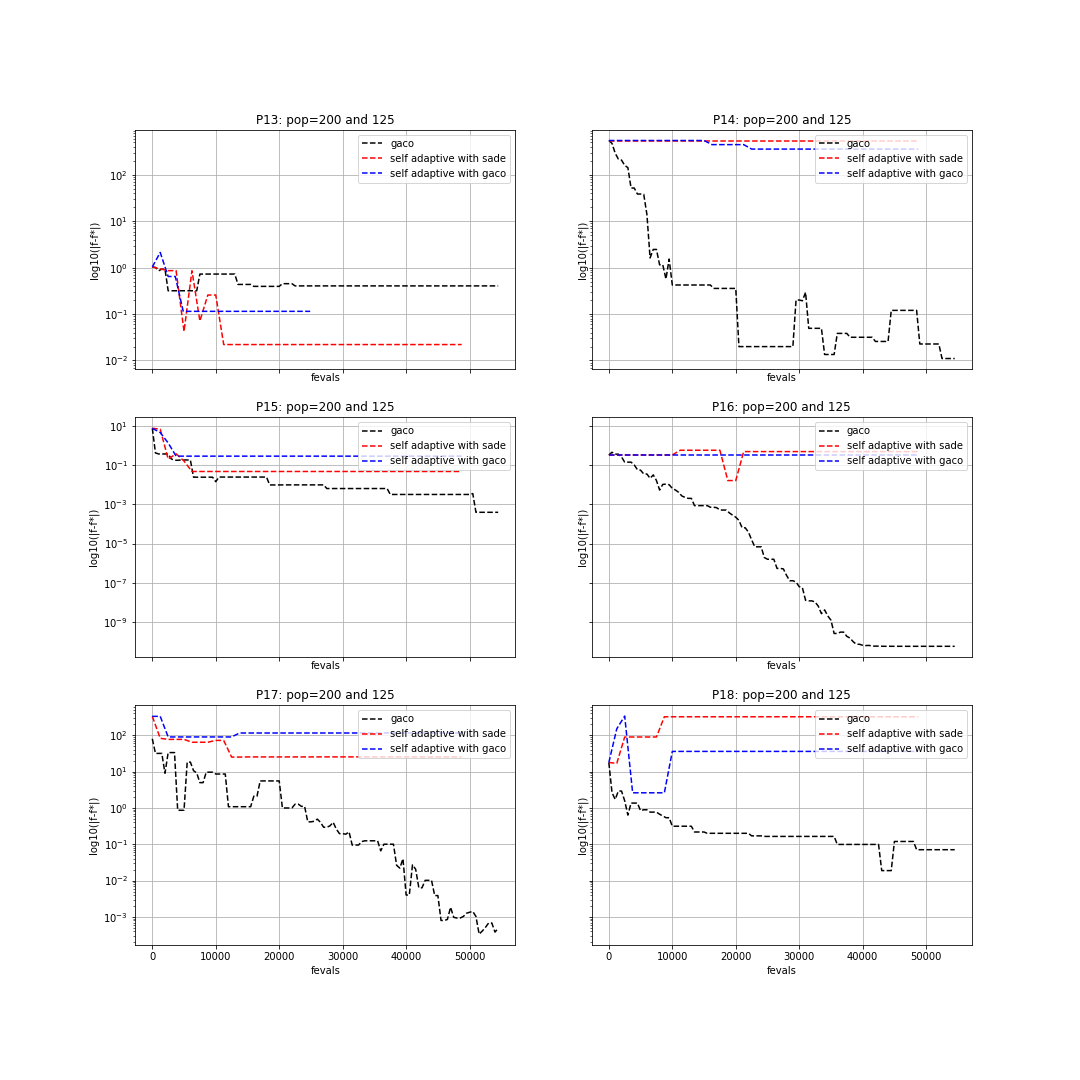
我们现在可以在半对数图中绘制结果,y轴是最佳适应度的绝对值减去已知最佳适应度,x轴是函数评估次数。为此,我们编写以下代码:
>>> import matplotlib as mlp
>>> import matplotlib.pyplot as plt
>>> fig, axes = plt.subplots(nrows=3, ncols=2, sharex='col', sharey='row', figsize=(15,15))
>>> axes[0,0].semilogy([entry[1] for entry in log_gaco_P13], [abs(entry[2]-real_minima[0]) for entry in log_gaco_P13],'k--', label = 'gaco')
>>> axes[0,0].semilogy([entry[1] for entry in log_sa_sade_P13], [abs(entry[2]-real_minima[0]) for entry in log_sa_sade_P13],'r--', label = 'self adaptive with sade')
>>> axes[0,0].semilogy([entry[1] for entry in log_sa_gaco_P13], [abs(entry[2]-real_minima[0]) for entry in log_sa_gaco_P13], 'b--', label = 'self adaptive with gaco')
>>> axes[0,0].legend(loc='upper right')
>>> axes[0,0].set_title('P13: pop=200 and 125')
>>> axes[0,1].semilogy([entry[1] for entry in log_gaco_P14], [abs(entry[2]-real_minima[1]) for entry in log_gaco_P14],'k--', label = 'gaco')
>>> axes[0,1].semilogy([entry[1] for entry in log_sa_sade_P14], [abs(entry[2]-real_minima[1]) for entry in log_sa_sade_P14],'r--', label = 'self adaptive with sade')
>>> axes[0,1].semilogy([entry[1] for entry in log_sa_gaco_P14], [abs(entry[2]-real_minima[1]) for entry in log_sa_gaco_P14], 'b--', label = 'self adaptive with gaco')
>>> axes[0,1].legend(loc='upper right')
>>> axes[0,1].set_title('P14: pop=200 and 125')
>>> axes[1,0].semilogy([entry[1] for entry in log_gaco_P15], [abs(entry[2]-real_minima[2]) for entry in log_gaco_P15],'k--', label = 'gaco')
>>> axes[1,0].semilogy([entry[1] for entry in log_sa_sade_P15], [abs(entry[2]-real_minima[2]) for entry in log_sa_sade_P15],'r--', label = 'self adaptive with sade')
>>> axes[1,0].semilogy([entry[1] for entry in log_sa_gaco_P15], [abs(entry[2]-real_minima[2]) for entry in log_sa_gaco_P15], 'b--', label = 'self adaptive with gaco')
>>> axes[1,0].legend(loc='upper right')
>>> axes[1,0].set_title('P15: pop=200 and 125')
>>> axes[1,1].semilogy([entry[1] for entry in log_gaco_P16], [abs(entry[2]-real_minima[3]) for entry in log_gaco_P16],'k--', label = 'gaco')
>>> axes[1,1].semilogy([entry[1] for entry in log_sa_sade_P16], [abs(entry[2]-real_minima[3]) for entry in log_sa_sade_P16],'r--', label = 'self adaptive with sade')
>>> axes[1,1].semilogy([entry[1] for entry in log_sa_gaco_P16], [abs(entry[2]-real_minima[3]) for entry in log_sa_gaco_P16], 'b--', label = 'self adaptive with gaco')
>>> axes[1,1].legend(loc='upper right')
>>> axes[1,1].set_title('P16: pop=200 and 125')
>>> axes[2,0].semilogy([entry[1] for entry in log_gaco_P17], [abs(entry[2]-real_minima[4]) for entry in log_gaco_P17],'k--', label = 'gaco')
>>> axes[2,0].semilogy([entry[1] for entry in log_sa_sade_P17], [abs(entry[2]-real_minima[4]) for entry in log_sa_sade_P17],'r--', label = 'self adaptive with sade')
>>> axes[2,0].semilogy([entry[1] for entry in log_sa_gaco_P17], [abs(entry[2]-real_minima[4]) for entry in log_sa_gaco_P17], 'b--', label = 'self adaptive with gaco')
>>> axes[2,0].legend(loc='upper right')
>>> axes[2,0].set_title('P17: pop=200 and 125')
>>> axes[2,1].semilogy([entry[1] for entry in log_gaco_P18], [abs(entry[2]-real_minima[5]) for entry in log_gaco_P18],'k--', label = 'gaco')
>>> axes[2,1].semilogy([entry[1] for entry in log_sa_sade_P18], [abs(entry[2]-real_minima[5]) for entry in log_sa_sade_P18],'r--', label = 'self adaptive with sade')
>>> axes[2,1].semilogy([entry[1] for entry in log_sa_gaco_P18], [abs(entry[2]-real_minima[5]) for entry in log_sa_gaco_P18], 'b--', label = 'self adaptive with gaco')
>>> axes[2,1].legend(loc='upper right')
>>> axes[2,1].set_title('P18: pop=200 and 125')
>>> for ax in axes.flat:
... ax.set(xlabel='fevals', ylabel='log10(|f-f*|)')
... ax.grid()
结果图可以在下图中看到: