基本多目标功能

在本教程中，我们将学习如何使用pygmo来解决多目标优化问题。我们假设您已经知道如何编写自己的多目标问题（UDP），因此这里将重点介绍一些旨在简化问题分析的附加功能。

让我们开始定义我们的总体：

>>> from pygmo import *
>>> udp = zdt(prob_id = 1)
>>> pop = population(prob = udp, size = 10, seed = 3453412)

我们在这里使用了ZDT基准测试套件中的第一个问题，该问题在zdt中实现，并且我们创建了一个population，其中包含在边界内随机创建的10个个体。哪些个体属于哪个非支配前沿？我们可以通过运行快速非支配排序算法fast_non_dominated_sorting()立即看到这一点：

>>> ndf, dl, dc, ndl = fast_non_dominated_sorting(pop.get_f()) 
[array([3, 4, 7, 8, 9], dtype=uint64), array([0, 5, 1, 6], dtype=uint64), array([2], dtype=uint64)]

不同非支配前沿的可视化也可以轻松获得。 例如，生成一个包含100个个体的新population：

>>> from matplotlib import pyplot as plt 
>>> pop = population(udp, 100)
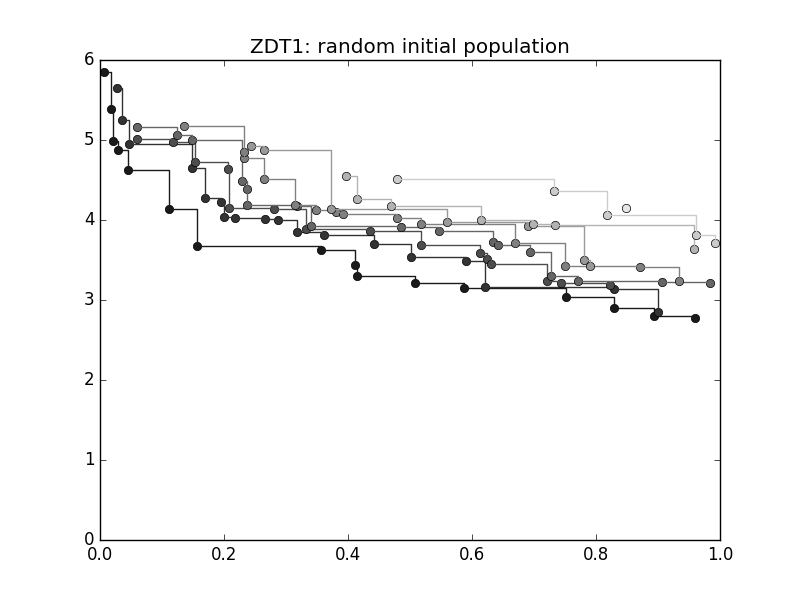
>>> ax = plot_non_dominated_fronts(pop.get_f()) 
>>> plt.ylim([0,6]) 
>>> plt.title("ZDT1: random initial population")  

其中每个连续的帕累托前沿以更深的颜色绘制。如果我们现在输入：

>>> algo = algorithm(moead(gen = 250))
>>> pop = algo.evolve(pop)
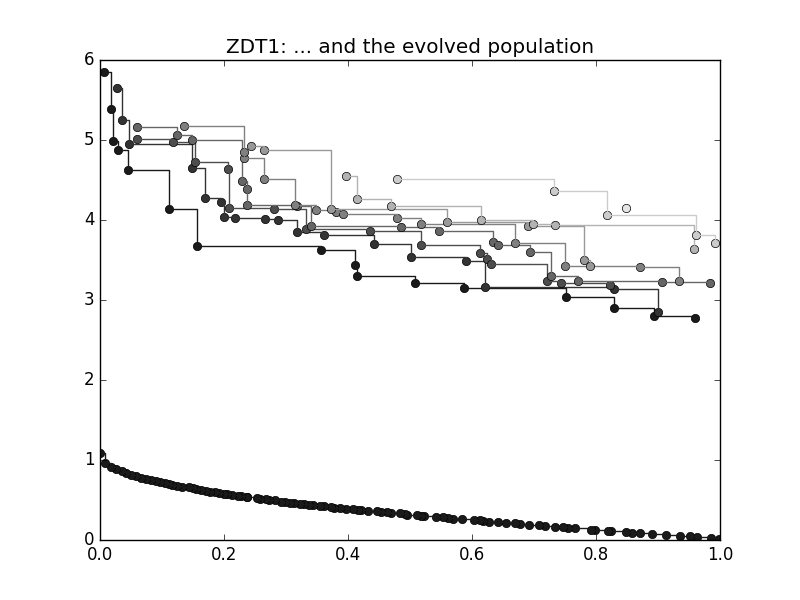
>>> ax = plot_non_dominated_fronts(pop.get_f()) 
>>> plt.title("ZDT1: ... and the evolved population")  

我们已经实例化了算法 moead，能够处理多目标问题，并将代数固定为250。在下一行中，我们直接使用算法的方法 pygmo.moead.evolve() 来进化 population

整个种群现在处于一个非支配前沿，可以通过输入以下内容轻松验证：

>>> ndf, dl, dc, ndl = fast_non_dominated_sorting(pop.get_f())
>>> print(ndf) 
[array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
       34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
       51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
       68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
       85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99], dtype=uint64)]

pygmo.zdt 问题套件中的问题（以及 pygmo.dtlz 中的问题）实现了一个称为 p_distance 的良好收敛度量。我们可以检查非支配前沿覆盖已知帕累托前沿的程度。

>>> udp.p_distance(pop) 
0.03926512747685471

如果我们对某个指标的值不满意，我们可以让种群进化更多代以提高这个数值：

>>> pop = algo.evolve(pop)
>>> udp.p_distance(pop) 
0.010346571321103046