近似超体积#

确定超体积指标是一项计算成本高昂的任务。 即使在维度相对较小且点数较少的情况下（例如，10维中的100个点）， 目前还没有已知的算法能够足够快地产生结果以供大多数多目标优化器使用。

在本教程中，我们将展示一种更快计算超体积指标的方法，但会牺牲一些准确性。 pygmo中包含两种算法，能够近似计算超体积：

  1. bf_fpras - 能够近似计算超体积指标

  2. bf_approx - 能够近似最小和最大的贡献者

注意

population 对象永远不会将计算委托给任何近似算法。 使用近似算法的唯一方式是通过显式请求 （有关如何执行此操作的更多信息，请参阅教程 高级超体积计算和分析 的开头部分）。

FPRAS#

在PyGMO中找到的类 bf_fpras 是一个完全多项式时间随机近似方案，通常用于计算超体积指标。您可以按以下方式调用FPRAS：

>>> import pygmo as pg
>>> prob = pg.problem(pg.dtlz(prob_id = 3, fdim=10, dim=11))
>>> pop = pg.population(prob, 100)
>>> fpras = pg.bf_fpras(eps=0.1, delta=0.1)
>>> hv = pg.hypervolume(pop)
>>> offset = 5
>>> ref_point = hv.refpoint(offset = 0.1)
>>> hv.compute(ref, hv_algo=fpras)

为了影响FPRAS的准确性，可以向其构造函数提供以下关键字参数：

  1. eps - 近似值的相对精度

  2. delta - 错误概率

对于给定的参数 eps=eps0 和 delta=delta0，所获得的解（以概率 1 - delta0）在精确超体积的 1 +/- eps0 倍范围内。

注意

eps 和 delta 越小，算法评估所需的时间就越长。

通过相对误差，我们指的是近似值在给定的数量级内是准确的，例如312.32和313.41在eps = 0.1内是准确的，因为它们在两个数量级内是准确的。同时，这些值在eps = 0.01内是不准确的。

运行时间#

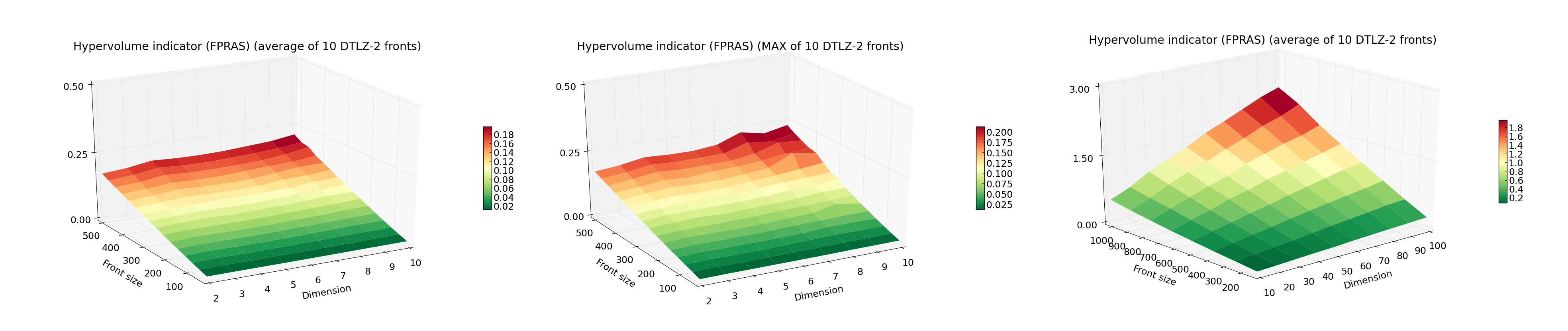
../_images/hv_fpras.png

图表展示了FPRAS在不同Front size和Dimension下的测量运行时间（10次中的平均值和最大值）。 该算法实例化时使用了eps=0.1和delta=0.1。 请注意，随着维度的增加，时间并没有出现任何指数级增长。

由于FPRAS在维度大小上扩展得非常好，我们还可以展示更大前沿大小和目标数量的数据。

现在，这真是一个了不起的成就！在100维空间中拥有1000个点的前沿，对于任何依赖精确计算的算法来说都是无法达到的。

最小贡献者的近似值#

除了FPRAS之外，pygmo还提供了一个专门用于计算最小/最大贡献者的近似算法。 当我们想要利用依赖于该特性的进化算法时，这非常有用，尤其是在问题具有多个目标时。

>>> # Problem with 30 objectives and 300 individuals
>>> prob = pg.problem(pg.dtlz(prob_id = 3, fdim=30, dim=35))
>>> pop = pg.population(prob, size = 300)
>>> hv_algo = pg.bf_approx(eps=0.1, delta=0.1)
>>> hv = pg.hypervolume(pop)
>>> offset = 5
>>> ref_point = hv.refpoint(offset = 0.1)
>>> hv.least_contributor(ref_point, hv_algo=hv_algo)

注意

bf_approx 仅提供两个功能 - 计算最小和最大贡献者。请求计算任何其他度量将引发异常。