超体积入门#
在多目标问题中,解的概念是非支配前沿。这些前沿的质量,即解的质量,可以通过多个指标来衡量。
其中一种衡量标准是超体积指标,它是非支配前沿(P)和参考点(R)之间的超体积。然而,严格计算该指标可能非常耗时,因此效率和近似方法可能非常重要。
在pygmo中,允许计算超体积指标(也称为Lebesgue测度或S度量)及相关量的主要功能由类hypervolume提供。从population或简单地从一个NumPy数组实例化这个类,将允许使用精确或近似算法计算超体积指标或单个点的独占贡献。
本教程将涵盖pygmo的超体积功能引入的特性。 首先,我们将描述用户界面的设计方式,并指出需要考虑的重要概念。 随后,我们将提供几个示例,以帮助您开始进行基本的超体积计算。
有关实现的算法及其性能的更多详细信息,请参阅出版物:
- Title
“最小超体积贡献者近似的实证表现。”
- Authors
克里斯托弗·诺瓦克,马库斯·马滕斯和达里奥·伊佐。
- Published in
自然并行问题解决国际会议。施普林格国际出版,2014年。
超体积接口和构建#
用于计算超体积指标(也称为Lebesgue测度或S度量)和超体积贡献的主要类是pygmo.hypervolume。您可以使用以下方式导入超体积类:
>>> from pygmo import hypervolume
>>> 'hypervolume' in dir()
True
由于超体积指标和超体积贡献的计算与多目标优化紧密相关,我们提供了两种构建hypervolume的方法。
第一种方法使用population中个体的适应度值作为输入点集:
>>> import pygmo as pg
>>> # Construct a DTLZ-2 problem with 3-dimensional fitness space and 10 dimensions
>>> udp = pg.problem(pg.dtlz(prob_id = 2, dim = 10, fdim = 3))
>>> pop = pg.population(udp, 50)
>>> hv = hypervolume(pop)
注意
如果种群的适应度值发生变化,您需要重建hypervolume。
点集保存在hypervolume中,并在构建时复制到那里。
第二种构建方法使用输入点集的显式坐标表示:
>>> from numpy import array
>>> hv = hypervolume(array([[1,0],[0.5,0.5],[0,1]]))
>>> hv_from_list = hypervolume([[1,0],[0.5,0.5],[0,1]])
这种构造类型特别有用,当您有一个明确的几何形状想要分析,而不是依赖于相应问题的目标函数的群体适应度值的隐式坐标时。
计算超体积指标和超体积贡献#
在我们概述每个超体积特征之前,让我们讨论一下我们对参考点和输入点集所做的假设,以确保其有效性:
1. 我们假设在每个维度上都进行最小化,也就是说,参考点在每个目标上都需要数值上更大或相等,并且至少在其中一个目标上严格更大。
2. 尽管一维的超体积在数学上有明确的定义,但我们要求任何输入数据的匹配维度至少为2,包括参考点。
pygmo 在这些假设方面为您提供帮助,因为它在构建时以及每次计算之前都会进行检查,如果您的输入集或参考点不符合这些标准,它将给您一个错误。
为了简单起见,我们将使用一个简单的二维前沿作为示例来展示超体积对象的基本特征:
>>> hv = hypervolume([[1, 0], [0.5, 0.5], [0, 1], [1.5, 0.75]] )
>>> ref_point = [2,2]
>>> hv.compute(ref_point)
3.25
我们将通过每个点在x轴上的位置来引用它们,例如第一个点是点(0,1),第四个点是(1.5, 0.75)等。下面的图表显示了示例的整体几何形状,参考点用红色标出。
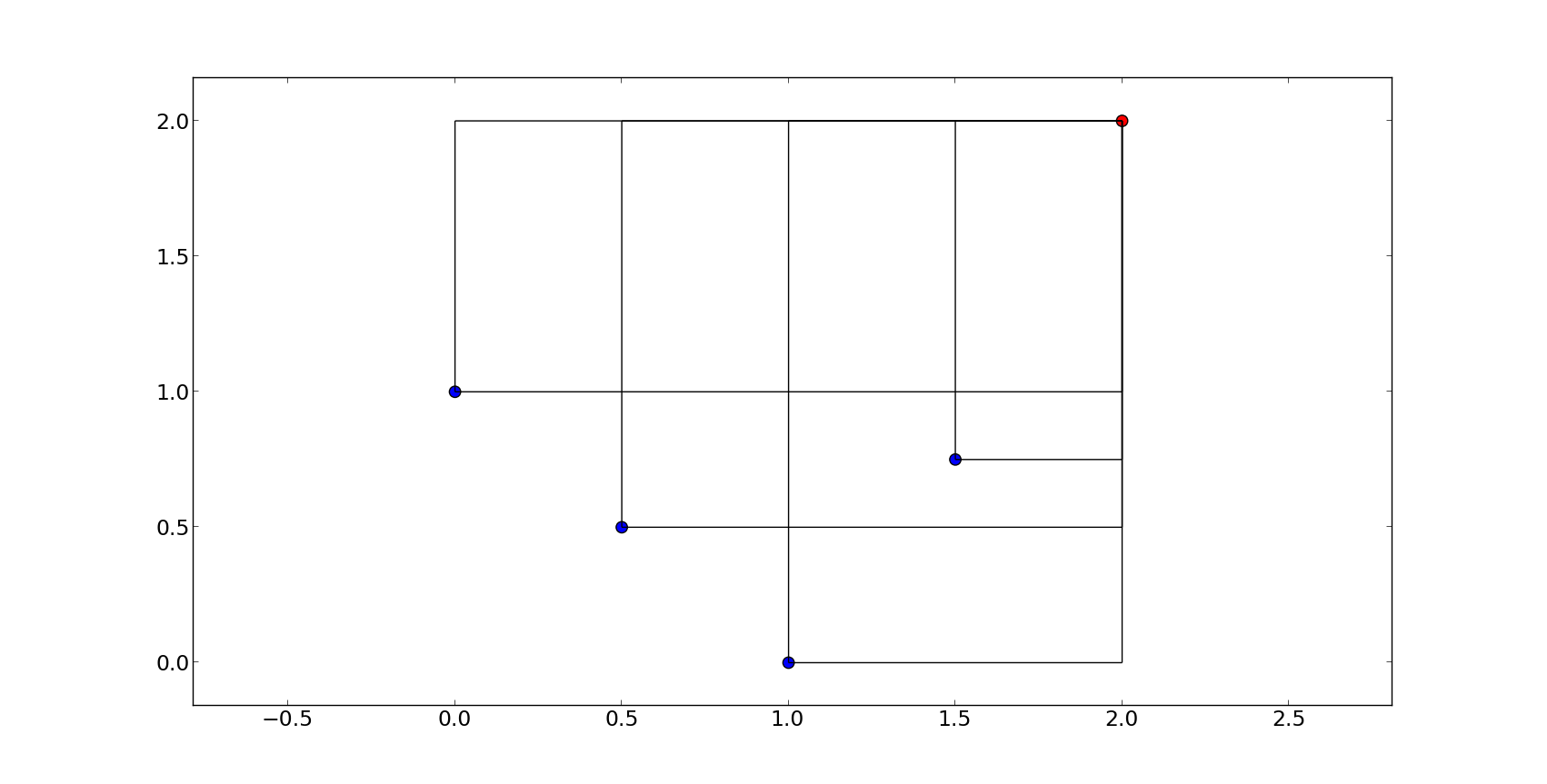
一旦创建了超体积对象,它允许计算以下数据:
compute()- 返回点集的联合超体积(S-度量)。
>>> # hv and ref_point refer to the data above
>>> hv.compute(ref_point)
3.25
exclusive()- 返回给定索引处点的独占超体积。 独占超体积 被定义为仅由一个点支配的空间部分,也称为其(超体积)贡献。
>>> # hv and ref_point refer to the data above
>>> hv.exclusive(1, ref_point)
0.25
>>> hv.exclusive(3, ref_point)
0.0
least_contributor()- 返回对超体积贡献最小的点的索引。
>>> # hv and ref_point refer to the data above
>>> hv.least_contributor(ref_point)
3
greatest_contributor()- 返回对超体积贡献最大的点的索引。
>>> # hv and ref_point refer to the data above
>>> hv.greatest_contributor(ref_point)
0
注意
在存在多个最小/最大贡献者的情况下,pygmo 会从所有候选者中任意返回一个贡献者。
contributions()- 返回集合中所有点的贡献列表。 这与依次调用exclusive()方法 对于每个点的结果相同。由于实现的原因,调用contributions()一次 可能比单独计算所有贡献要快得多(最多可达线性因子) 通过使用exclusive()。
>>> # hv and ref_point refer to the data above
>>> hv.contributions(ref_point)
array([0.5 , 0.25, 0.5 , 0. ])
由于上述所有方法都需要一个参考点,因此使用nadir()自动生成一个参考点是非常有用的。
以下简短的脚本利用了上述提到的一些特性,展示了population进化后的超体积增加。
>>> import pygmo as pg
>>> # Instantiates a 4-objectives problem
>>> prob = pg.problem(pg.dtlz(prob_id=4, dim = 12, fdim=4))
>>> pop = pg.population(prob, 84)
>>> # Construct the hypervolume object
>>> # and get the reference point off-setted by 10 in each objective
>>> hv = pg.hypervolume(pop)
>>> offset = 5
>>> ref_point = hv.refpoint(offset = 0.1)
>>> hv.compute(ref_point)
10.75643
>>> # Evolve the population some generations
>>> algo = pg.algorithm(pg.moead(gen=2000))
>>> pop = algo.evolve(pop)
>>> # Compute the hypervolume indicator again.
>>> # This time we expect a higher value as SMS-EMOA evolves the population
>>> # by trying to maximize the hypervolume indicator.
>>> hv = pg.hypervolume(pop)
>>> hv.compute(ref_point)
18.73422